Dieser Artikel vermittelt Ihnen relevantes Wissen über Java Der Prime-Algorithmus ist ein umfassender Suchalgorithmus zum Erstellen eines minimalen Spannbaums aus einem verbundenen Diagramm. In diesem Artikel werden hauptsächlich das Prinzip und die Implementierung des Prime-Algorithmus in Java vorgestellt. Wenn Sie interessiert sind, können Sie sich darüber informieren.
Empfohlenes Lernen: „Java-Video-Tutorial“
Behandeln Sie beim Spanning Tree die Knoten, die sich bereits im Spanning Tree befinden, und Setzen Sie den Rest. Die Knoten werden als eine weitere Menge betrachtet, und die Kante mit dem geringsten Gewicht kann aus den Kanten ausgewählt werden, die die beiden Mengen verbinden.
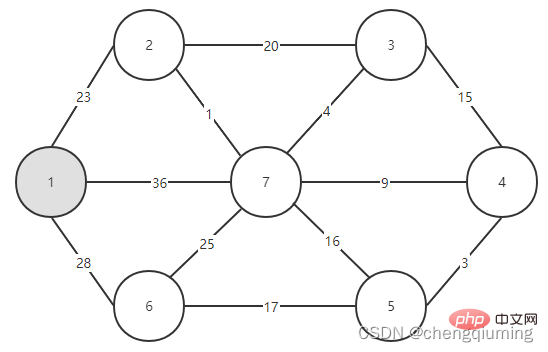
Wählen Sie zuerst einen Knoten aus, z. B. Knoten 1, und fügen Sie ihn in die Menge U, U = {1} ein. Die verbleibenden Knoten sind dann V-U = {2,3,4, 5 ,6,7}, die Menge V ist die Menge aller Knoten des Graphen.
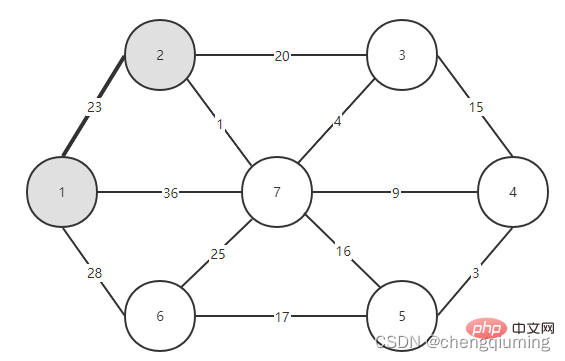
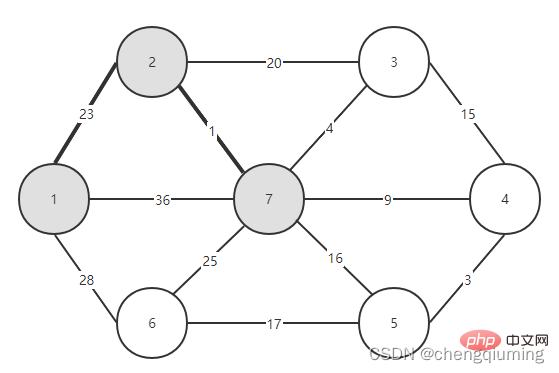
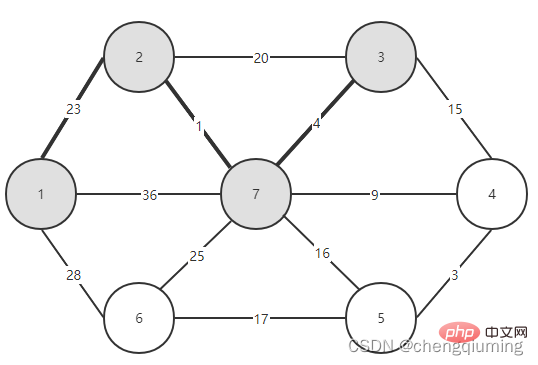
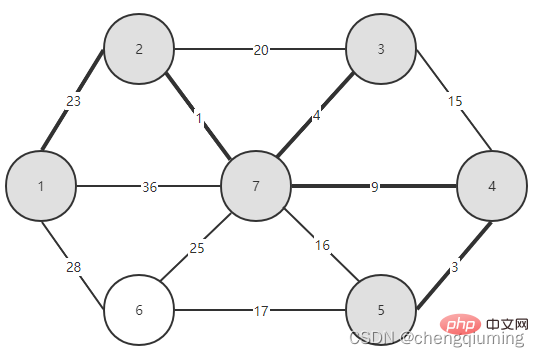
Jetzt müssen Sie nur noch sehen, welche Kante unter den Kanten, die die beiden Mengen (U und V-U) verbinden, das kleinste Gewicht hat, und den Knoten, der der Kante mit dem kleinsten Gewicht zugeordnet ist, zur Menge U hinzufügen. Wie aus der obigen Abbildung ersichtlich ist, hat Kante 1-2 von den drei Kanten, die die beiden Mengen verbinden, das kleinste Gewicht. Wählen Sie sie aus und fügen Sie Knoten 2 zur Menge U, U={1,2}, V - U= hinzu { 3,4,5,6}, wie in der Abbildung unten gezeigt.
Wählen Sie dann aus den Kanten, die die beiden Sätze (U und V-U) verbinden, die Kante mit dem geringsten Gewicht aus. Wie aus der obigen Abbildung ersichtlich ist, ist unter den vier Kanten, die die beiden Mengen verbinden, das Kantengewicht von Knoten 2 bis Knoten 7 am kleinsten. Wählen Sie diese Kante aus und fügen Sie Knoten 7 zur Menge U = {1,2,7} hinzu. , V-U ={3,4,5,6}.
Fahren Sie so fort, bis U=V endet und der aus der ausgewählten Kante und allen Knoten bestehende Graph der minimale Spannbaum ist. Das ist Prims Algorithmus.
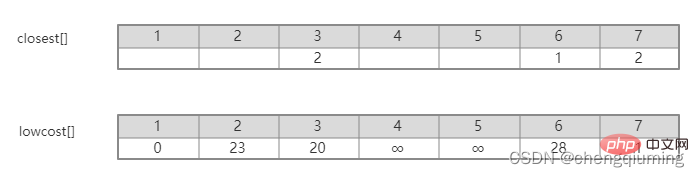
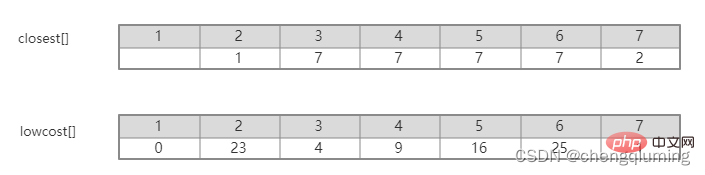
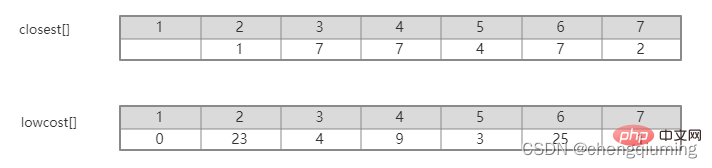
Wenn man das Bild intuitiv betrachtet, kann man leicht herausfinden, welche Kante von der Menge U zur Menge U-V das kleinste Gewicht hat. Allerdings ist der Zeitaufwand zu hoch, um diese Kanten im Programm vollständig aufzuzählen und dann das Minimum zu finden Wert. Dieses Problem kann geschickt gelöst werden, indem ein Array festgelegt wird. Closet[j] stellt den nächsten Nachbarpunkt vom Knoten j in der Menge V-U zur Menge U dar. Lowcost[j] stellt den Kantenwert vom Knoten j in der Menge V-U zum nächsten Nachbarpunkt dar setze U. Das heißt, das Gewicht der Kante (j, am nächsten [j]).
In der obigen Abbildung ist beispielsweise der nächste Nachbarpunkt von Knoten 7 zur Menge U 2, cloeest[7]=2. Der Kantenwert vom Knoten 7 zum nächsten Nachbarpunkt 2 beträgt 1, was dem Gewicht der Kante (2,7) entspricht und als lowcost[7]=1 aufgezeichnet wird, wie in der folgenden Abbildung dargestellt.
Suchen Sie also einfach den niedrigsten Lowcost[]-Knoten in der Menge V - U.
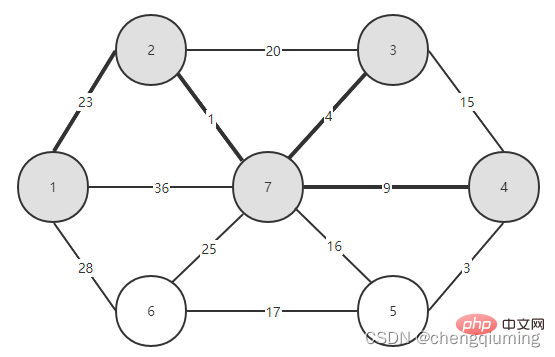
1. Lassen Sie die Menge U={u0}, u0 zu V gehören und initialisieren Sie die Arrays close[], lowcost[] und s[].
2. Finden Sie den Knoten t mit dem kleinsten Lowcost-Wert in der Menge V-U, d. h. lowcost[t]=min{lowcost[j]},j gehört zu V-U. Der Knoten t, der diese Formel erfüllt, ist der nächstgelegene Punkt U in der Menge V-U verbinden.
3. Füge Knoten t zur Menge U hinzu.
4. Wenn die Menge V – U leer ist, endet der Algorithmus, andernfalls fahren Sie mit Schritt 5 fort.
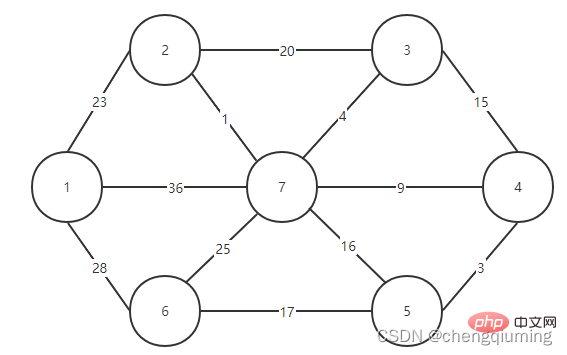
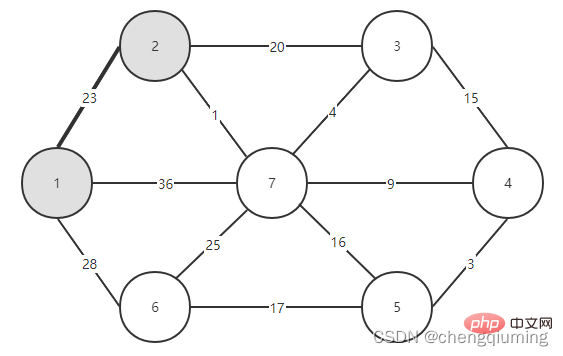
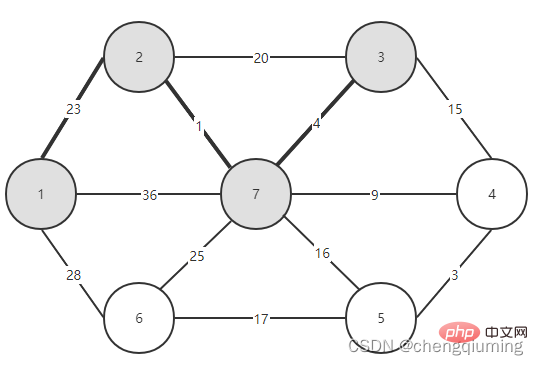
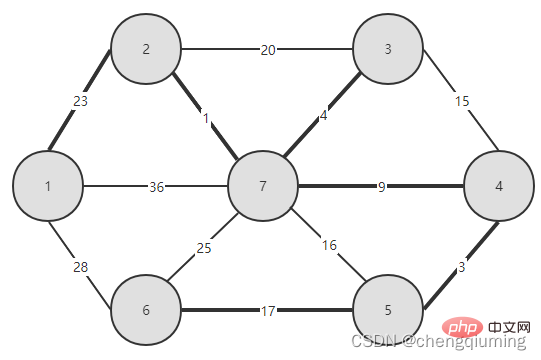
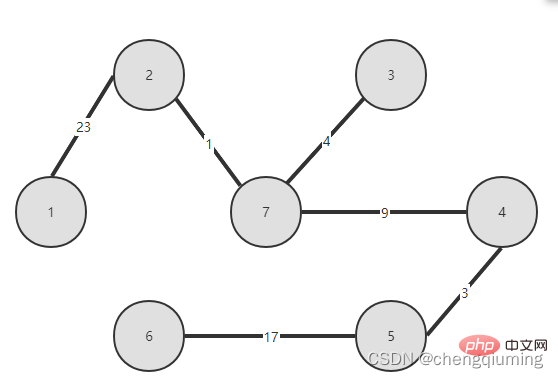
5. Aktualisieren Sie seine Lowcost[] und Nearest[] für alle Knoten j in der Menge V-U. if(C[t][j] Befolgen Sie die oben genannten Schritte, und schließlich erhalten Sie einen Spannbaum mit der kleinsten Gewichtssumme. 4. Diagramm 2 Finden Sie den Knoten mit den geringsten Kosten, entsprechend t=2. Die ausgewählten Kanten und Knoten sind wie unten dargestellt. 3 wird zur Menge U hinzugefügt. Fügen Sie den Knoten t zur Menge U, U={1,2} hinzu und aktualisieren Sie gleichzeitig V-U={3,4,5,6,7} 4. Für jeden benachbarten Punkt j von t in der Menge V-U kann dieser mit Hilfe von t aktualisiert werden. Die benachbarten Punkte von Knoten 2 sind Knoten 3 und Knoten 7. C[2][3]=20 C[2][7]= 1< lowcost[7]=36, aktualisieren Sie die Entfernung des nächsten Nachbarn lowcost[7]=1, den nächsten Nachbarn nächstgelegene[7]=2; Die aktualisierten nächstgelegenen [] und lowcost[] sind in der folgenden Abbildung dargestellt. Der aktualisierte Satz sieht wie folgt aus: 5 Suchen Sie den Knoten mit den kleinsten Niedrigkosten, entsprechend t=7, und die ausgewählten Kanten und Knoten sind wie unten dargestellt. 6 Zum Set U hinzufügen. Fügen Sie den Knoten t zur Menge U, U={1,2,7} hinzu und aktualisieren Sie gleichzeitig V-U={3,4,5,6} 7. Für jeden benachbarten Punkt j von t in der Menge V-U kann dieser mit Hilfe von t aktualisiert werden. Die benachbarten Punkte von Knoten 7 sind die Knoten 3, 4, 5 und 6. Der aktualisierte nächstgelegene[] und günstigste[] sind in der folgenden Abbildung dargestellt. Der aktualisierte Satz sieht wie folgt aus: 8 Suchen Sie den Knoten mit den kleinsten Niedrigkosten, entsprechend t=3, und die ausgewählten Kanten und Knoten sind wie unten dargestellt. 9 zu Set U hinzugefügt. Fügen Sie den Knoten t zur Menge U, U={1,2,3,7} hinzu und aktualisieren Sie gleichzeitig V-U={4,5,6} 10. Für jeden benachbarten Punkt j von t in der Menge V-U kann dieser mit Hilfe von t aktualisiert werden. Der Nachbar von Knoten 3 ist Knoten 4. C[3][4]=15>lowcost[4]=9, die Arrays closest[] und lowcost[] ändern sich nicht. Der aktualisierte Satz sieht wie folgt aus: 11 Finden Sie den Knoten mit den kleinsten niedrigsten Kosten, entsprechend t=4, und die ausgewählten Kanten und Knoten sind wie unten gezeigt. 12 zu Set U hinzugefügt. Fügen Sie den Knoten t zur Menge U, U={1,2,3,4,7} hinzu und aktualisieren Sie gleichzeitig V-U={5,6} 13. Für jeden benachbarten Punkt j von t in der Menge V-U kann dieser mit Hilfe von t aktualisiert werden. Der Nachbar von Knoten 4 ist Knoten 5. 🔜 unten dargestellt. C[5][6]=17 Der aktualisierte Satz ist wie folgt: 17 Finden Sie den Knoten mit den geringsten Kosten, entsprechend t=6. Die ausgewählten Kanten und Knoten sind wie unten dargestellt. 18 zu Set U hinzugefügt. Fügen Sie den Knoten t zur Menge U, U={1,2,3,4,5,6,7} hinzu und aktualisieren Sie gleichzeitig V-U={} 19. Für jeden benachbarten Punkt j von t in der Menge V-U kann dieser mit Hilfe von t aktualisiert werden. Knoten 6 hat keine benachbarten Punkte in der Menge V-U. Closest[] und lowcost[] müssen nicht aktualisiert werden. 20 Der erhaltene minimale Spannbaum ist wie folgt. Die Summe der Gewichte des minimalen aufspannenden Baums beträgt 57 Empfohlene Studie: „ Das obige ist der detaillierte Inhalt vonDas Prinzip und die Implementierung des Prime-Algorithmus in Java (Zusammenfassungsfreigabe). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!Der Graph G=(V,E) ist ein ungerichteter verbundener gewichteter Graph, wie in der Abbildung unten dargestellt.
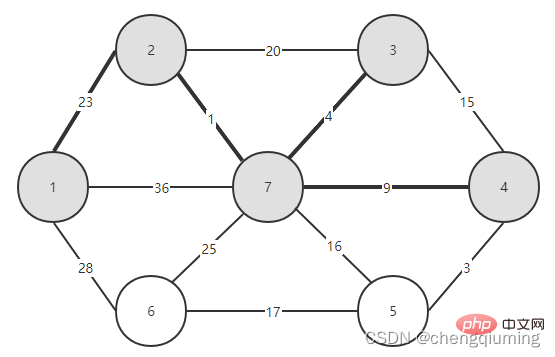
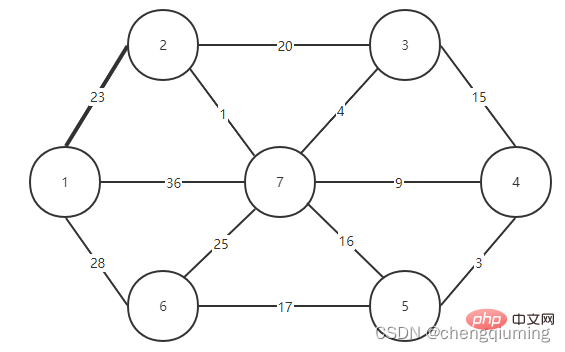1 Initialisierung. Angenommen, u0 = 1, sei die Menge U = {1}, die Menge V-U = {2,3,4,5,6,7}, s[1] = wahr, initialisiere das Array am nächsten []: außer Knoten 1, Alle anderen Knoten sind 1, was bedeutet, dass die nächsten Nachbarpunkte von den Knoten in der Menge V-U zur Menge U alle 1 sind.lowcost[]: Der Kantenwert von Knoten 1 zum Knoten in der Menge V-U. „nest[]“ und „lowcost[]“ sind in der folgenden Abbildung dargestellt. 
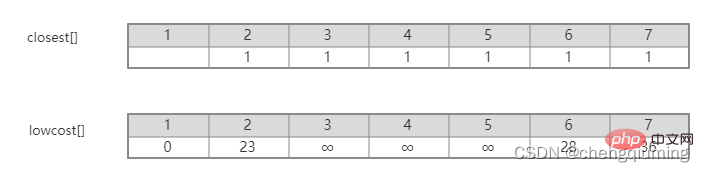Das Bild nach der Initialisierung ist: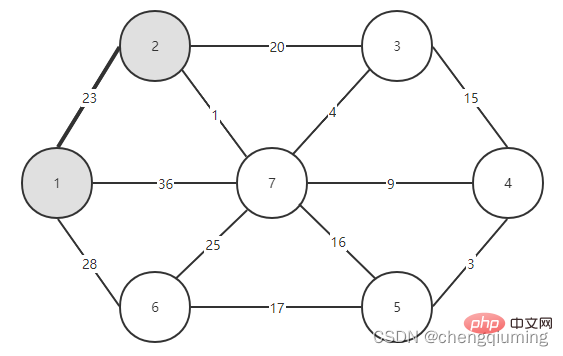 
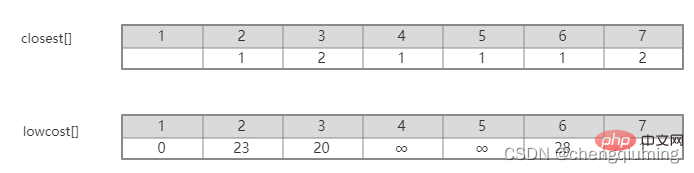
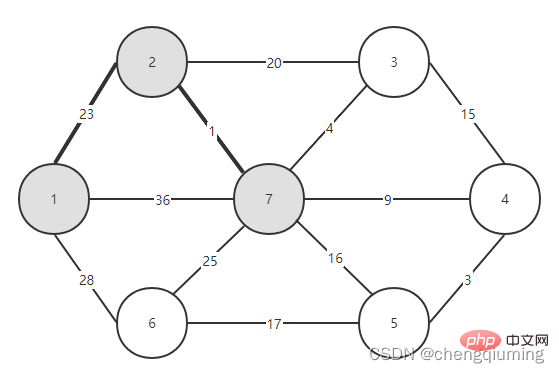
16. Für jeden benachbarten Punkt j von t in der Menge V-U kann dieser mit Hilfe von t aktualisiert werden. Der Nachbar von Knoten 5 ist Knoten 6.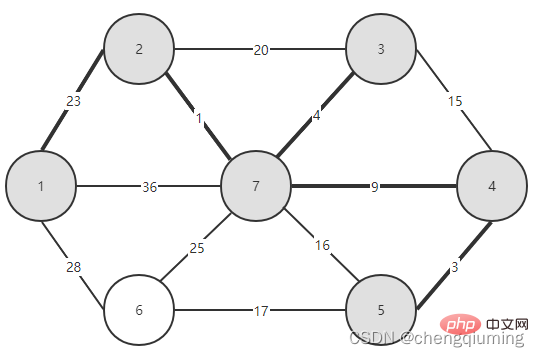 
Java-Video-Tutorial
![Eingehende JavaScript-Analyse [Web-Frontend muss über Grundkenntnisse verfügen]](https://img.php.cn/upload/course/000/000/041/61d3ff1c83b43350.jpg)
![Grundlegende JavaScript-Syntax [dom|bom|es6 neue Syntax|jQuery|Datenvisualisierungs-Echarts]](https://img.php.cn/upload/course/000/000/068/6242bb730fb11708.png)
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
