 Themen
Themen
 excel
excel
 Was ist das Lösen in einer Variablen? Excel-Lösungsfallanalyse mit einer einzelnen Variablen
Was ist das Lösen in einer Variablen? Excel-Lösungsfallanalyse mit einer einzelnen Variablen
Was ist das Lösen in einer Variablen? Excel-Lösungsfallanalyse mit einer einzelnen Variablen
Wenn Sie als Finanzbeamter befördert werden und eine Gehaltserhöhung erhalten möchten, müssen Sie nicht nur in der Lage sein, Statistiken zu zählen, sondern auch einige Datenvorhersagen basierend auf den Anforderungen des Unternehmens zu treffen. Sie müssen in Excel sehr komplexe mathematische Operationen durchführen. Es stellt uns ein Tool zur Verfügung, mit dem wir Datenvorhersagen problemlos durchführen können, nämlich die Excel-Funktion zum Lösen einzelner Variablen.

Analyse und Prognose werden heutzutage immer wichtigerer Bestandteil der Arbeit von Finanzpersonal. Die gebräuchlichste und effektivste Methode ist die univariate Analyse. Es gibt viele Methoden zur Durchführung einer univariaten Analyse, z. B. die Interpolationsmethode, die Versuch-und-Irrtum-Methode usw. Aber für einen Excel-Experten ist die Lösung mit einer Variablen zweifellos die beste Antwort.
1. Was ist eine Einzelvariablenlösung?
Wie in der folgenden Abbildung dargestellt, ist Zelle B2 eine Konstante und Zelle B4 das Ergebnis einer bestimmten Operation an B2. Wir können den Wert von B2 ändern, sodass sich auch B4 ändert. Hier nennen wir B2 die variable Zelle und B4 die Zielzelle.

Diese sequentielle Berechnung ist sehr einfach. Beispielsweise ist B2 95 und B4 200. Hier stellt sich also die Frage: Wenn wir möchten, dass die Zielzelle (B4) einem bestimmten Wert entspricht, wie sollten wir dann den entsprechenden Wert der variablen Zelle (B2) lösen? Genau wie in der Grundschulmathematik wissen wir, dass der X-Wert verwendet werden kann, um den Y-Wert zu ermitteln, aber wie findet man den X-Wert basierend auf dem Y-Wert? Sie benötigen Hilfe bei einem Variablenlöser. Eine Variablenlösung ist die Umkehroperation der Funktionsformel.
Wo also die Einzelvariablenlösung in Excel ist, sowie die Prinzipien der Einzelvariablenlösung in Excel und Excel-Einzelvariablenlösungsfälle, verraten wir Ihnen in diesem Artikel.
Zum Beispiel gehen wir davon aus, dass der Zielwert 250 ist. Der spezifische Vorgang ist wie folgt:
Schritt 01 Klicken Sie auf die Excel-Registerkarte [Daten] – [Simulationsanalyse] – [Einzelvariable Lösung], um das zu öffnen Dialogfeld „Lösung mit einer einzelnen Variablen“.

Schritt 02 Stellen Sie im Dialogfeld die Zielzelle auf $B$4 ein, geben Sie dann manuell den Zielwert der Zielzelle als 250 ein und setzen Sie die Variablenzelle auf $B$2. Wie unten gezeigt.

Es ist zu beachten, dass der Zielwert von 250 nicht zufällig festgelegt wird, sondern die folgenden zwei Bedingungen erfüllen muss:
1. Es handelt sich um eine Ganzzahl oder eine Dezimalzahl, Text oder logischer Wert können nicht eingegeben werden
2. Es sollte im Zielzellenwertbereich enthalten sein, d. h. es gibt einen variablen Zellenwert, der den Zielzellenwert dem Zielwert gleicht. Andernfalls wird die Lösung mit einer Variablen länger ausgeführt und führt schließlich zu einer Lösung, die den Anforderungen entspricht Die Konditionen können nicht eingeholt werden.
Schritt 03 Klicken Sie auf die Schaltfläche „OK“, um eine Einzelvariablenlösung durchzuführen. Excel führt automatisch iterative Operationen durch und erhält schließlich den Variablenzellenwert (120), wenn die Zielzelle (B4) gleich dem Zielwert (250) ist, und weist ihn automatisch der Variablenzelle (B2) zu. Klicken Sie wie unten gezeigt auf OK. 2. Excel-Lösungsbeispiel für eine einzelne Variable eine fünfjährige Laufzeit von der Bank. Das Darlehen beträgt 35 Millionen RMB und der Darlehensbetrag und die Zinsen werden in gleichen monatlichen Raten zurückgezahlt. Basierend auf dem anfänglichen jährlichen Zinssatzplan der Bank von 6,3 % errechnete Mitarbeiter A, dass Unternehmen A 681.500 pro Monat zahlen müsste.
Wie in der folgenden Abbildung dargestellt, können Sie mit der Formel: =PMI (Jahreszinssatz/12, Anzahl der Perioden, Kreditbetrag) berechnen, dass die monatlichen Rückzahlungszinsen 681.500 betragen.
Nach der Berechnung dürften die für die Kreditrückzahlung verfügbaren Mittel jedoch nur 675.000 pro Monat betragen, nachdem das Unternehmen den Kredit erhalten hat. Der Finanzdirektor bat Mitarbeiter A, den für das Unternehmen akzeptablen jährlichen Höchstzinssatz zu berechnen, um mit der Bank verhandeln zu können. Ein Mitarbeiter hat analysiert, dass Zelle B5 des jährlichen Zinssatzes eine variable Zelle ist, B6 der monatlichen Kapital- und Zinsrückzahlung die Zielzelle ist und der Zielwert 67,5 ist. Ist das nicht genau eine einzelne variable Lösung?
Schritt 01 Klicken Sie entsprechend der eingestellten Datenbeziehung auf die Schaltfläche [Einzelne Variable lösen], stellen Sie die Zielzelle auf $B$6, den Zielwert auf 67,5 und die Variablenzelle auf $B$5 ein, klicken Sie [OK], um fortzufahren. Schritt 02 Nach der iterativen Operation liefert Excel schnell eine Lösung, die die Bedingungen erfüllt. Klicken Sie auf [OK], um die Einzelvariablenlösung abzuschließen. Wie unten gezeigt. Aus der obigen Tabelle können wir ersehen, dass der maximale jährliche Zinssatz, den das Unternehmen akzeptieren kann, 5,9 % beträgt. Dies ist eine Lösung mit einer Variablen, die nicht nur effizient, sondern auch genau ist! Excel-Einzelvariablenlösungsfall 2 Äquivalentzinsproblem Mitarbeiter B ist Investmentmanager eines Unternehmens und plant den Erwerb eines neuen Projekts und erfordert eine Investition von 1,6 Milliarden Yuan (derzeit). (Wert der kumulierten Investition), der geplante Stückpreis beträgt 18.800, und die durchschnittliche Zahlungsfrist wird voraussichtlich 5 Jahre betragen. Nach der Berechnung beträgt der entsprechende Zinssatz der Investition des Unternehmens in dieses Projekt 8,8 %. Wie in der folgenden Abbildung dargestellt, können Sie mit der Formel: =RRI (Rückzahlungszeitraum, Barwert der Gesamtinvestition, Umsatzerlös) den tatsächlichen äquivalenten Zinssatz des aktuellen Investitionswerts entsprechend dem zukünftigen Wert berechnen. Gemäß den internen Vorgaben des Unternehmens darf der investitionsäquivalente Zinssatz für ein Milliardenprojekt nicht weniger als 10 % betragen, daher muss der Verkaufspreis angepasst werden. Mitarbeiter B verwendet den Verkaufspreis B3 als Variablenzelle, den entsprechenden Zinssatz B8 als Zielzelle und der Zielwert beträgt 10 %. Schritt 01 Klicken Sie entsprechend der eingestellten Datenbeziehung auf die Schaltfläche [Einzelne Variable lösen], setzen Sie die Zielzelle auf $B$8, den Zielwert auf 10 %, die Variablenzelle auf $B$3 und Klicken Sie auf [OK]. Führen Sie eine Einzelvariablenlösung durch. Schritt 02 Nach dem iterativen Vorgang stellt Excel schnell eine Lösung bereit, die die Bedingungen erfüllt. Klicken Sie auf [OK], um die Einzelvariablenlösung abzuschließen. Wie im Bild oben gezeigt, können wir die Ergebnisse sehen. Der Mindestverkaufspreis wurde auf 19.879,09 Yuan angepasst, was den Anforderungen des Unternehmens entsprechen kann. Excel-Einzelvariablenlösungsfall 3 Break-Even-Point-Problem Mitarbeiter C ist der Finanzmanager eines Produktionsunternehmens. Das Unternehmen verfügt über eine Fabrik, die aufgrund der schlechten Marktleistung reduziert werden soll bis 200.000. Mitarbeiter C. Berechnen Sie den Gewinn und Verlust der Fabrik bei dieser Leistung. Es ist bekannt, dass der durchschnittliche Verkaufspreis von Produkten mit steigender Produktion sinkt und die drei Gebühren in einem bestimmten Verhältnis zu Umsatz und Einkommen stehen. Nach der Berechnung beträgt der Gesamtgewinn bei einer Produktion von 200.000 Yuan 13,8368 Millionen Yuan. Wie unten gezeigt. Die Marktleistung der Produkte des Unternehmens ist weiterhin rückläufig. Die Unternehmensleitung erwägt eine weitere Reduzierung der Produktion und ist verpflichtet, die Produktion im Bereich der Gewinnschwelle zu steuern. Mitarbeiter C dachte darüber nach und verwendete die Ausgabe B3 als Variablenzelle, den Gesamtgewinn B12 als Zielzelle, und der Zielwert war 0, und die Break-Even-Ausgabe wurde auf einmal berechnet. Schritt 01 Klicken Sie entsprechend der eingestellten Datenbeziehung auf die Schaltfläche [Einzelne Variable lösen], setzen Sie die Zielzelle auf $B$12, den Zielwert auf 0 und die Variablenzelle auf $B$3, klicken Sie [OK], um fortzufahren. Schritt 02 Nach dem iterativen Vorgang stellt Excel schnell eine Lösung bereit, die die Bedingungen erfüllt. Klicken Sie auf [OK], um die Einzelvariablenlösung abzuschließen. Anhand des Bildes oben können wir sehen, dass das Unternehmen ein Produktionsvolumen von rund 81.900 kontrolliert, was die Gewinnschwelle erreichen kann. Eine Lösung mit einer Variablen kann als leistungsstarke und unbeliebte Anwendung in Excel angesehen werden. Es hat das Gefühl, dass es „sinnlos ist, es zu sagen, aber es ist anstrengend, wenn man es nicht sagt“. In der Vergangenheit haben Sie möglicherweise viel Zeit damit verbracht, diese Art von Einzelvariablenanalyseproblemen manuell zu lösen. Von nun an können Sie sich von solch ineffizienter Arbeit befreien und die Einzelvariablenlösung wird zu Ihrem rechten Assistenten . Verwandte Lernempfehlungen: Excel-Tutorial
Das obige ist der detaillierte Inhalt vonWas ist das Lösen in einer Variablen? Excel-Lösungsfallanalyse mit einer einzelnen Variablen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1374
1374
 52
52
 Was soll ich tun, wenn die Rahmenlinie beim Drucken in Excel verschwindet?
Mar 21, 2024 am 09:50 AM
Was soll ich tun, wenn die Rahmenlinie beim Drucken in Excel verschwindet?
Mar 21, 2024 am 09:50 AM
Wenn wir beim Öffnen einer Datei, die gedruckt werden muss, feststellen, dass die Tabellenrahmenlinie aus irgendeinem Grund in der Druckvorschau verschwunden ist, müssen wir uns rechtzeitig darum kümmern, wenn dies auch in Ihrem Ausdruck erscheint file Wenn Sie Fragen wie diese haben, dann schließen Sie sich dem Editor an, um den folgenden Kurs zu erlernen: Was soll ich tun, wenn die Rahmenlinie beim Drucken einer Tabelle in Excel verschwindet? 1. Öffnen Sie eine Datei, die gedruckt werden muss, wie in der Abbildung unten gezeigt. 2. Wählen Sie alle erforderlichen Inhaltsbereiche aus, wie in der Abbildung unten dargestellt. 3. Klicken Sie mit der rechten Maustaste und wählen Sie die Option „Zellen formatieren“, wie in der Abbildung unten gezeigt. 4. Klicken Sie oben im Fenster auf die Option „Rahmen“, wie in der Abbildung unten gezeigt. 5. Wählen Sie links das dünne, durchgezogene Linienmuster im Linienstil aus, wie in der Abbildung unten gezeigt. 6. Wählen Sie „Äußerer Rand“
 So filtern Sie in Excel mehr als 3 Schlüsselwörter gleichzeitig
Mar 21, 2024 pm 03:16 PM
So filtern Sie in Excel mehr als 3 Schlüsselwörter gleichzeitig
Mar 21, 2024 pm 03:16 PM
Excel wird im Büroalltag häufig zur Verarbeitung von Daten verwendet und es ist oft notwendig, die Funktion „Filter“ zu nutzen. Wenn wir uns für die „Filterung“ in Excel entscheiden, können wir nur bis zu zwei Bedingungen für dieselbe Spalte filtern. Wissen Sie also, wie man in Excel mehr als drei Schlüsselwörter gleichzeitig filtert? Lassen Sie mich es Ihnen als Nächstes demonstrieren. Die erste Methode besteht darin, die Bedingungen schrittweise zum Filter hinzuzufügen. Wenn Sie drei qualifizierende Details gleichzeitig herausfiltern möchten, müssen Sie zunächst eines davon Schritt für Schritt herausfiltern. Zu Beginn können Sie anhand der Konditionen zunächst Mitarbeiter mit dem Namen „Wang“ herausfiltern. Klicken Sie dann auf [OK] und aktivieren Sie dann in den Filterergebnissen die Option [Aktuelle Auswahl zum Filter hinzufügen]. Die Schritte sind wie folgt. Führen Sie die Filterung ebenfalls separat erneut durch
 So ändern Sie den Kompatibilitätsmodus für Excel-Tabellen in den Normalmodus
Mar 20, 2024 pm 08:01 PM
So ändern Sie den Kompatibilitätsmodus für Excel-Tabellen in den Normalmodus
Mar 20, 2024 pm 08:01 PM
Bei unserer täglichen Arbeit und beim Lernen kopieren wir Excel-Dateien von anderen, öffnen sie, um Inhalte hinzuzufügen oder sie erneut zu bearbeiten, und speichern sie dann. Manchmal wird ein Dialogfeld zur Kompatibilitätsprüfung angezeigt, was sehr problematisch ist Software, kann es in den Normalmodus geändert werden? Im Folgenden wird Ihnen der Herausgeber detaillierte Schritte zur Lösung dieses Problems vorstellen. Lassen Sie uns gemeinsam lernen. Denken Sie abschließend daran, es zu speichern. 1. Öffnen Sie ein Arbeitsblatt und zeigen Sie im Namen des Arbeitsblatts einen zusätzlichen Kompatibilitätsmodus an, wie in der Abbildung dargestellt. 2. In diesem Arbeitsblatt wird nach dem Ändern des Inhalts und dem Speichern immer das Dialogfeld des Kompatibilitätsprüfers angezeigt. Es ist sehr schwierig, diese Seite zu sehen, wie in der Abbildung gezeigt. 3. Klicken Sie auf die Office-Schaltfläche, klicken Sie auf Speichern unter und dann
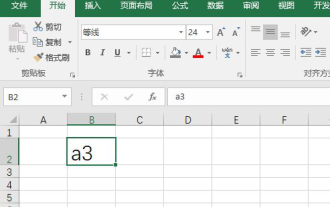 So geben Sie den Index in Excel ein
Mar 20, 2024 am 11:31 AM
So geben Sie den Index in Excel ein
Mar 20, 2024 am 11:31 AM
eWir verwenden häufig Excel, um einige Datentabellen usw. zu erstellen. Manchmal müssen wir bei der Eingabe von Parameterwerten eine bestimmte Zahl hochstellen oder tiefstellen Schauen Sie sich die detaillierten Schritte an: 1. Hochgestellte Methode: 1. Geben Sie zunächst a3 (3 ist hochgestellt) in Excel ein. 2. Wählen Sie die Zahl „3“, klicken Sie mit der rechten Maustaste und wählen Sie „Zellen formatieren“. 3. Klicken Sie auf „Hochgestellt“ und dann auf „OK“. 4. Schauen Sie, der Effekt ist so. 2. Tiefgestellte Methode: 1. Geben Sie ähnlich wie bei der hochgestellten Einstellungsmethode „ln310“ (3 ist der tiefgestellte Index) in die Zelle ein, wählen Sie die Zahl „3“ aus, klicken Sie mit der rechten Maustaste und wählen Sie „Zellen formatieren“. 2. Aktivieren Sie „Tiefstellen“ und klicken Sie auf „OK“.
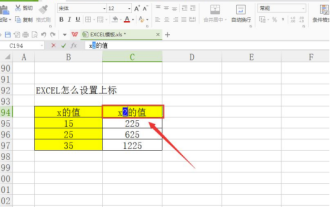 So setzen Sie in Excel hochgestellt
Mar 20, 2024 pm 04:30 PM
So setzen Sie in Excel hochgestellt
Mar 20, 2024 pm 04:30 PM
Bei der Verarbeitung von Daten stoßen wir manchmal auf Daten, die verschiedene Symbole wie Vielfache, Temperaturen usw. enthalten. Wissen Sie, wie man in Excel hochgestellte Zeichen setzt? Wenn wir Excel zum Verarbeiten von Daten verwenden und keine hochgestellten Zeichen setzen, wird die Eingabe vieler unserer Daten schwieriger. Heute stellt Ihnen der Editor die spezifische Einstellungsmethode für Excel-Hochstellung vor. 1. Öffnen wir zunächst das Microsoft Office Excel-Dokument auf dem Desktop und wählen Sie den Text aus, der hochgestellt werden soll, wie in der Abbildung gezeigt. 2. Klicken Sie dann mit der rechten Maustaste und wählen Sie die Option „Zellen formatieren“ im Menü, das nach dem Klicken erscheint, wie in der Abbildung gezeigt. 3. Als nächstes im Dialogfeld „Zellen formatieren“, das automatisch angezeigt wird
 So verwenden Sie die iif-Funktion in Excel
Mar 20, 2024 pm 06:10 PM
So verwenden Sie die iif-Funktion in Excel
Mar 20, 2024 pm 06:10 PM
Die meisten Benutzer verwenden Excel, um Tabellendaten zu verarbeiten. Abgesehen von Experten haben nicht viele Benutzer diese Funktion beim Schreiben in VBA verwendet Die Funktionen der Funktionen sind ähnlich. Lassen Sie mich Ihnen die Verwendung der iif-Funktion vorstellen. Es gibt iif-Funktionen in SQL-Anweisungen und VBA-Code in Excel. Die iif-Funktion ähnelt der IF-Funktion im Excel-Arbeitsblatt. Sie führt eine Beurteilung von wahren und falschen Werten durch und gibt unterschiedliche Ergebnisse basierend auf den logisch berechneten wahren und falschen Werten zurück. IF-Funktionsverwendung ist (Bedingung, ja, nein). IF-Anweisung und IIF-Funktion in VBA Die erstere IF-Anweisung ist eine Steueranweisung, die je nach Bedingungen unterschiedliche Anweisungen ausführen kann, während die letztere
 Wo wird der Excel-Lesemodus eingestellt?
Mar 21, 2024 am 08:40 AM
Wo wird der Excel-Lesemodus eingestellt?
Mar 21, 2024 am 08:40 AM
Beim Studium von Software sind wir es gewohnt, Excel zu verwenden, nicht nur, weil es praktisch ist, sondern auch, weil es eine Vielzahl von Formaten erfüllen kann, die in der tatsächlichen Arbeit benötigt werden, und Excel sehr flexibel zu verwenden ist, und es gibt einen Modus dafür Praktisch zum Lesen. Heute habe ich für alle mitgebracht: Wo man den Excel-Lesemodus einstellt. 1. Schalten Sie den Computer ein, öffnen Sie dann die Excel-Anwendung und suchen Sie die Zieldaten. 2. Es gibt zwei Möglichkeiten, den Lesemodus in Excel festzulegen. Der erste: In Excel gibt es eine Vielzahl praktischer Verarbeitungsmethoden, die im Excel-Layout verteilt sind. In der unteren rechten Ecke von Excel gibt es eine Verknüpfung zum Festlegen des Lesemodus. Klicken Sie darauf, um in den Lesemodus zu gelangen. Auf der rechten Seite des Kreuzstrichs befindet sich eine kleine dreidimensionale Markierung .
 So fügen Sie Excel-Symbole in PPT-Folien ein
Mar 26, 2024 pm 05:40 PM
So fügen Sie Excel-Symbole in PPT-Folien ein
Mar 26, 2024 pm 05:40 PM
1. Öffnen Sie die PPT und blättern Sie zu der Seite, auf der Sie das Excel-Symbol einfügen müssen. Klicken Sie auf die Registerkarte Einfügen. 2. Klicken Sie auf [Objekt]. 3. Das folgende Dialogfeld wird angezeigt. 4. Klicken Sie auf [Aus Datei erstellen] und dann auf [Durchsuchen]. 5. Wählen Sie die einzufügende Excel-Tabelle aus. 6. Klicken Sie auf OK und die folgende Seite wird angezeigt. 7. Aktivieren Sie [Als Symbol anzeigen]. 8. Klicken Sie auf OK.












