Dieser Artikel vermittelt Ihnen relevantes Wissen über Java, das hauptsächlich die Transformation von Zufallsfunktionen in Java vorstellt. Der Beispielcode im Artikel ist hilfreich, damit wir Java lernen können Erfahren Sie mehr.
Empfohlene Studie: „Java-Video-Tutorial“
gelöste Probleme
Problem 1
In Java gibt die Funktion Math.random() ein Intervall mit gleicher Wahrscheinlichkeit zurück [0,1) Eine beliebige Dezimalzahl. Das heißt, im Fall von x < 1 beträgt die Wahrscheinlichkeit, dass die Zahl in [0,x) erscheint Ich möchte x < 1 wird die Wahrscheinlichkeit der Zahl in [0,x) auf x^2 angepasst . Was ist zu tun? Math.random()函数是等概率返回区间[0,1)中的任意一个小数。即x < 1情况下，[0,x)中的数出现的的概率是x，如果我们要将x < 1情况下，[0,x)中的数出现的的概率调整成x^2，应该如何做？
问题1思路
由于[0,x)的概率是x，那么调用两次Math.random()，如果较大的那个值也要在[0,x)区间内，那么两次调用都必须在[0,x)区间内（因为任意一次在[x,1)都会导致返回值不在[0,x)上），即概率是x^2，代码如下
package snippet;
public class Code_0004_RandToPow2 {
// 将`[0,x)`中的数出现的的概率调整成`x^2`
public static double randToPow2() {
return Math.max(Math.random(), Math.random());
}
}Nach dem Login kopieren
我们可以通过如下测试代码来验证问题1的解法：
package snippet;
public class Code_0004_RandToPow2 {
// 将`[0,x)`中的数出现的的概率调整成`x^2`
public static double randToPow2() {
return Math.max(Math.random(), Math.random());
}
// 测试用例
public static void main(String[] args) {
int count = 0;
int testTimes = 10000000;
double x = 0.17;
for (int i = 0; i < testTimes; i++) {
if (randToPow2() < x) {
count++;
}
}
System.out.println((double) count / (double) testTimes);
System.out.println(Math.pow(x, 2));
}
}Nach dem Login kopieren
打印的结果如下
0.0288603
0.028900000000000006
接近目标要求。
问题2
假设我们有一个随机函数f()，这个函数可以等概率返回[1,5]中的一个数，如何只利用f()函数而不引入其他随机函数，得到一个等概率返回[1,7]中任意一个数的函数g()。
思路
由于目标是求[1,7]等概率返回一个，如果我们能加工得到一个x()函数，这个函数是等概率返回[0,6]范围内的任意一个数，那么目标函数g()只需要调用这个x()函数再加上1，即是g()函数要求
public static int g() {
return x() + 1;
}Nach dem Login kopieren
要得到[0,6]等概率返回一个数，我们需要先得到一个0和1等概率返回的随机函数m()，我们可以通过f()函数来得到，即
// 通过[0,5]等概率返回的随机函数f()
// 加工出等概率得到0和1
// 1,2,3,4,5 五个数
// 得到1，2的时候，返回0
// 得到4，5的时候，返回1
// 得到3的时候，弃而不用，再次尝试
public static int m() {
int ans = 0;
do {
ans = f();
} while (ans == 3);
return ans < 3 ? 0 : 1;
}Nach dem Login kopieren
有了等概率返回 0 和 1 的随机函数 m()， 我们可以很方便的生成[0,6]随机等概率返回一个数的方法，因为[0,6]需要三个二进制数表示，那么我们可以调用三次m()函数，可以等概率得到[0,7]范围内任意一个数，我们可以在得到 7 的时候，重试上述过程，只有结果在[0,6]才返回，这样就加工出了x()函数。
// 等概率返回0~6
public static int x() {
int ans = 0;
do {
ans = (m() << 2) + (m() << 1) + m();
} while (ans == 7);
return ans;
}Nach dem Login kopieren
最后，目标函数f()通过如下方式
// 等概率返回1~7
public static int g() {
return x() + 1;
}Nach dem Login kopieren
即可得到。完整代码如下
package snippet;
public class Code_0005_Rand5ToRand7 {
// 此函数只能用，不能修改
// 等概率返回1~5
public static int f() {
return (int) (Math.random() * 5) + 1;
}
// 通过[0,5]等概率返回的随机函数f()
// 加工出等概率得到0和1
// 1,2,3,4,5 五个数
// 得到1，2的时候，返回0
// 得到4，5的时候，返回1
// 得到3的时候，弃而不用，再次尝试
public static int m() {
int ans = 0;
do {
ans = f();
} while (ans == 3);
return ans < 3 ? 0 : 1;
}
// 等概率返回0~6
public static int x() {
int ans = 0;
do {
ans = (m() << 2) + (m() << 1) + m();
} while (ans == 7);
return ans;
}
// 等概率返回1~7
public static int g() {
return x() + 1;
}
}Nach dem Login kopieren
问题3
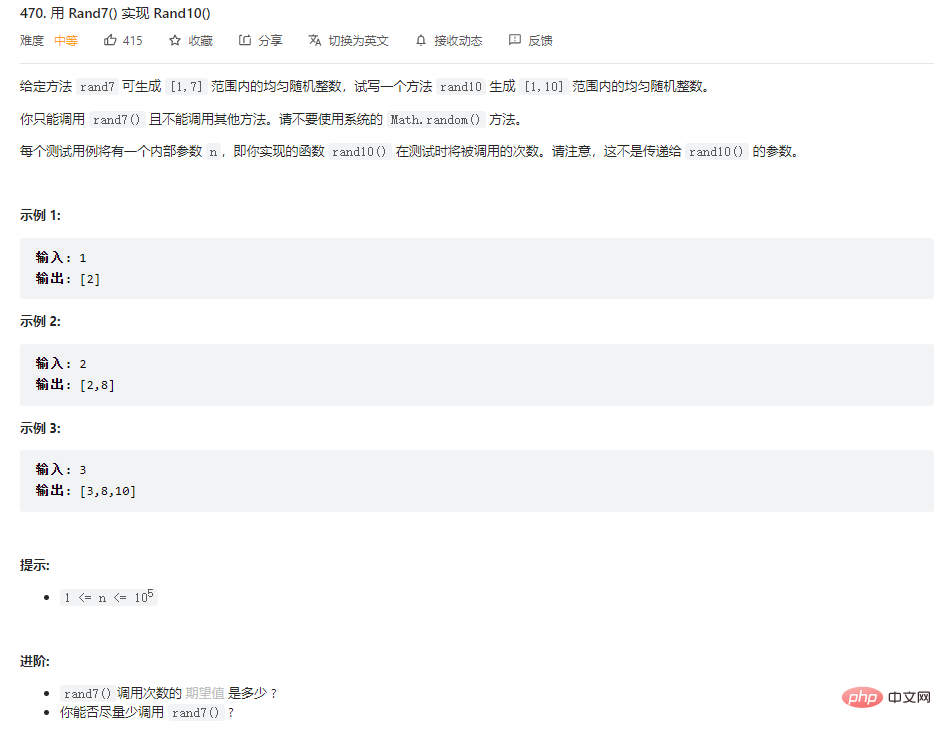
和问题2思路一致，核心都是要先实现一个等概率返回 0 和 1 的随机函数m()。，然后看目标函数区间需要几个二进制位，来决定调用几次m()函数，不赘述，完整代码见
/**
* The rand7() API is already defined in the parent class SolBase.
* public int rand7();
* @return a random integer in the range 1 to 7
*/
class Solution extends SolBase {
public int rand10() {
return rand(10);
}
public int rand(int N) {
int bit = 1;
int base = 2;
while (base <= N) {
base = 2 << bit;
bit++;
}
int v = build(bit);
while (v < 1 || v > N) {
v = build(bit);
}
return v;
}
private int build(int bit) {
int v = 0;
for (int i = 0; i < bit; i++) {
v += (m() << i);
}
return v;
}
// 核心：生成 0 和 1 等概率返回的随机函数
public int m() {
int i = rand7();
while (i == 7) {
i = rand7();
}
return (i == 1 || i == 2 || i == 3) ? 0 : 1;
}
}Nach dem Login kopieren
问题4
有一个函数f()，不等概率（但是是固定概率）返回0和1，如何只通过f()函数，得到等概率返回 0 和 1 的随机函数g()，
思路，
调用两次f()函数，可以得到如下情况
0 0
1 1
0 1
1 0
当两次都是0，或者两次都是1的时候，舍弃，虽然 0 和 1 的概率不一样，但是
0 1
1 0
概率一定一样
所以得到 0 1就返回 0 ，得到 1 0就返回1，即g()
Idee für Frage 1
Da die Wahrscheinlichkeit von
[0,x) x ist, rufen Sie
Math.random() zweimal auf. Wenn der größere Wert auch innerhalb des
[0,x)-Intervalls liegen muss, müssen beide Aufrufe innerhalb des
[0,x)-Intervalls liegen (da jeder Zeitpunkt innerhalb des < code>[0,x) Intervallcode>[x,1) führt dazu, dass der Rückgabewert nicht auf
[0,x) liegt, d. h Wahrscheinlichkeit ist
x^2, der Code lautet wie folgt:
package snippet;
// 不等概率随机函数变成等概率随机函数
public class Code_0005_EqualProbabilityRandom {
// 不等概率函数，
// 内部内容不可见
public static int f() {
return Math.random() < 0.8 ? 0 : 1;
}
// 等概率返回0和1
public static int g() {
int first;
do {
first = f(); // 0 1
} while (first == f());
return first;
}
}Nach dem Login kopieren
rrreeeDie gedruckten Ergebnisse lauten wie folgt🎜
🎜0,0288603
0,028900000000000006🎜
🎜Nah an den Zielanforderungen. 🎜
Frage 2
🎜Angenommen, wir haben eine Zufallsfunktion
f(). Diese Funktion kann mit gleicher Wahrscheinlichkeit eine Zahl in
[1,5] zurückgeben , wie man
nur die Funktion f() verwendet, ohne andere Zufallsfunktionen einzuführen, und eine gleiche Wahrscheinlichkeit erhält, eine beliebige Zahl in
[1,7] zurückzugeben code> Die Funktion <code>g(). 🎜🎜Idee🎜🎜Da das Ziel darin besteht,
[1,7] mit gleicher Wahrscheinlichkeit zurückzugeben, wird diese Funktion, wenn wir eine
x()-Funktion verarbeiten können, mit gleicher Wahrscheinlichkeit zurückgegeben Wahrscheinlichkeit Eine beliebige Zahl im Bereich von
[0,6], dann muss die Zielfunktion
g() nur diese Funktion
x() aufrufen plus 1, das heißt, die Funktion
g() erfordert 🎜rrreee🎜, dass
[0,6] eine Zahl mit gleicher Wahrscheinlichkeit zurückgibt, das müssen wir tun Holen Sie sich zuerst eine 0 und eine 1. Die Zufallsfunktion
m(), die die gleiche Wahrscheinlichkeit zurückgibt, kann über die Funktion
f() erhalten werden, also 🎜rrreee 🎜 hat die gleiche Wahrscheinlichkeit, 0 und 1 zurückzugeben. Mit der Zufallsfunktion
m() können wir ganz einfach
[0,6] generieren, eine Methode zur zufälligen Rückgabe einer Zahl mit gleicher Wahrscheinlichkeit. weil
[0,6] Wir benötigen drei Binärzahlen zur Darstellung, dann können wir die Funktion
m() dreimal aufrufen und jede Zahl im Bereich von erhalten
[0,7] mit gleicher Wahrscheinlichkeit. Wir können den obigen Vorgang wiederholen, wenn wir 7 erhalten, und nur das Ergebnis wird zurückgegeben, wenn
[0,6] und somit verarbeitet wird
x()-Funktion. 🎜rrreee🎜Schließlich kann die Zielfunktion
f() wie folgt erhalten werden 🎜rrreee🎜. Der vollständige Code lautet wie folgt: 🎜rrreee
Frage 3
🎜🎜Die Idee ist die gleiche wie bei Frage 2. Der Kern besteht darin,zuerst eine Zufallsfunktion m() zu implementieren gibt mit gleicher Wahrscheinlichkeit 0 und 1 zurück. , und schauen Sie sich dann an, wie viele Binärbits im Zielfunktionsintervall benötigt werden, um zu entscheiden, wie oft die Funktion m() aufgerufen werden soll Vollständiger Code, siehe 🎜rrreee
Frage 4
🎜Es gibt eine Funktion
f(), die 0 und 1 mit ungleicher Wahrscheinlichkeit (aber fester Wahrscheinlichkeit) zurückgibt 0 und 1 nur über die Funktion
f() zurückgeben? Die Zufallsfunktion
g() von 1, 🎜🎜Idee, 🎜🎜ruft den
f() zweimal ausführen, können Sie die folgende Situation erhalten: 🎜<blockquote>🎜0 0<br>1 1<br>0 1<br>1 0🎜</blockquote>🎜Wenn beide Zeiten 0 sind, oder beide Zeiten sind 1, verwerfen Sie sie, obwohl die Wahrscheinlichkeiten von 0 und 1 unterschiedlich sind, 🎜 <blockquote>🎜0 1<br>1 0🎜</blockquote>🎜Die Wahrscheinlichkeit muss gleich sein🎜🎜, wenn Sie also bekommen <code>0 1, Sie geben 0 zurück, wenn Sie
1 0 erhalten, geben Sie 1 zurück. Die
g()-Funktion🎜🎜Der vollständige Code lautet wie folgt🎜rrreee🎜Empfohlenes Lernen: „🎜Java-Video-Tutorial🎜“🎜
Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung von Beispielen für die Transformation zufälliger Funktionen in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
