So finden Sie Primzahlen in Javascript

So finden Sie Primzahlen: 1. Durchlaufen Sie alle natürlichen Zahlen im Bereich 1~n und dividieren Sie sie durch n. Wenn der Rest 0 ist, bedeutet dies, dass die Zahl n keine Primzahl ist, andernfalls ist sie eine Primzahl . Die Syntax „for(i=2;i

Die Betriebsumgebung dieses Tutorials: Windows 7-System, JavaScript-Version 1.8.5, Dell G3-Computer.

Das Konzept der Primzahlen

Primzahlen werden auch Primzahlen genannt. Eine Primzahl bezieht sich auf eine Zahl, die nicht durch andere natürliche Zahlen außer 1 und sich selbst unter den natürlichen Zahlen größer als 1 teilbar ist.

Primzahlen innerhalb von 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 25 insgesamt.

Vier Möglichkeiten, Primzahlen mit JavaScript zu bestimmen

1. Primzahlen können nur durch 1 und sich selbst teilbar sein

Primzahlen können nur durch 1 und sich selbst geteilt werden, durchlaufen Sie also alle natürlichen Zahlen in der (1, n) offenes Intervall zur Division durch n. Wenn es eine ganzzahlige Division gibt, das heißt, der Rest ist 0, bedeutet dies, dass die Zahl n keine Primzahl ist, andernfalls ist sie eine Primzahl.

function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>Aber die Komplexität dieses Algorithmus ist O(n)</p><h3 id="strong-und-der-Bereich-der-Quadratwurzeln-von-Primzahlen-strong"><strong>2 und der Bereich der Quadratwurzeln von Primzahlen</strong></h3><p>Angenommen, n ist keine Primzahl, dann kann n nicht nur durch 1 und geteilt werden n, kann aber auch durch i und j geteilt werden. Das heißt, 15 ist keine Primzahl, 15 / 3 = 5. Beispielsweise ist 35 keine Primzahl , 35 / 5 = 7. Zu diesem Zeitpunkt müssen i und j in (1, Math.sqrt(n) ] und [Math.sqrt(n), n) sein, zum Beispiel Math.sqrt(15) ≈ 3,8 , dann ist 3 in (1, 3.8] und 5 ist in [3.8, 15). Beispiel: Math.sqrt(4) = 2, dann ist 2 in (1,2] und auch in [2,4). </p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>Derzeit beträgt die Komplexität des Algorithmus O(sqrt(n))</p><h3 id="strong-Primzahlen-können-keine-anderen-geraden-Zahlen-außer-sein-strong"><strong>3. Primzahlen können keine anderen geraden Zahlen außer 2 sein</strong></h3><p>Mit Ausnahme von 2 sind alle geraden Zahlen keine Primzahlen</p><p><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/image/644/149/762/1663645614907138.png" class="lazy" title="1663645614907138.png" alt="So finden Sie Primzahlen in Javascript"> </p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  if (n % 2 === 0) {
    return false;
  }
 
  for (let i = 3; i <p>n in der for-Schleife, nur der hellblaue Teil des Bildes oben. </p><p>Der obige Algorithmus reduziert also die Schleife um die Hälfte und die Zeitkomplexität beträgt O(sqrt(n) / 2) </p><p>Es ist zu beachten, dass der Code dieses Algorithmus die Beurteilungsbedingung von n % 2 === nicht hinzufügen kann 0 zur Schleife, der folgende Code weist eine Sicherheitslücke auf</p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 3; i <p>Zu diesem Zeitpunkt werden 4, 6 und 8 alle als Primzahlen beurteilt. </p><p>Der Grund für die Sicherheitslücke ist, dass die Schleifenbedingung i </p><p>Dieser Algorithmus kann nur garantieren, dass der n-Wert von n korrekt ist, wenn die Schleifenbedingung i = i^2 = 9. </p><h3 id="strong-Primzahlen-größer-oder-gleich-müssen-an-Vielfache-von-angrenzen-strong"><strong>4. Primzahlen größer oder gleich 5 müssen an Vielfache von 6 angrenzen</strong></h3><p>Primzahlen größer oder gleich 5 müssen an Vielfache von 6 angrenzen</p><p> (Beachten Sie, dass dieser Satz nicht äquivalent ist zu: <span style="text-decoration:line-through;"> liegt neben Vielfachen von 6. Die benachbarte Zahl muss eine Primzahl größer als 5 sein</span>, diese Schlussfolgerung ist nicht wahr)</p><p><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/image/674/593/865/1663645632699688.png" class="lazy" title="166364562667908So finden Sie Primzahlen in Javascript" alt="So finden Sie Primzahlen in Javascript"></p><p>Wie in der Abbildung oben gezeigt, werden Zahlen größer oder gleich 5 unterteilt in: 6y -1, 6y, 6y+1, 6y+2, 6y +3, 6y+4 (y>=1)</p><p>Unter diesen können 6y, 6y+2, 6y+3 und 6y+4 keine Primzahlen sein . Nur 6y-1 und 6y+1<strong><span   style="max-width:90%">können</span></strong>Primzahlen sein. </p><p>Darüber hinaus sind 6y-1 (y>=1) und 6y + 5 (y>=0) gleichwertig. </p><p>Wir können also die Zahlen direkt ausschließen, bei denen n nicht 6y-1 (oder 6y+5) und 6y+1 ist. Die Eliminierungsmethode lautet: </p><pre class='brush:php;toolbar:false;'>  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }

Als nächstes müssen wir 6y-1 (oder 6y+5) eliminieren ) und 6y Die Nicht-Primzahl in +1,

  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }

Hier gibt es möglicherweise zwei Dinge, die Sie verwirren:

• Warum das Inkrement von i in der for-Schleife 6
• Warum ist die Bedingung für die Bestimmung Primzahlen in der for-Schleife n % i = == 0 ||. n % (i+2) === 0

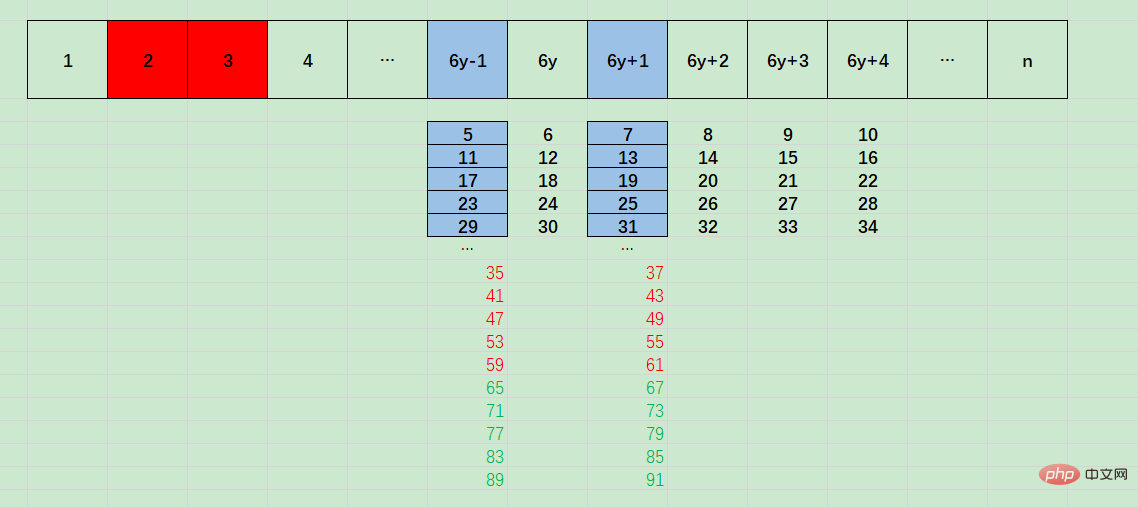
Wenn wir uns das Diagramm oben ansehen, können wir feststellen, dass 6y-1 eine Arithmetik ist Folge mit einer Basis von 5 und einer Differenz von 6. Das ist 5 + 6x :

• 对于 5 + 6x 而言，如果x为5的倍数（5 * z），则5 + 6x = 5 + 6 * 5 * z = 5 *（1+6z）,则此时5 + 6x可以被5整除。
• 5 + 6x 还可以转化为 5 + 6 + 6 * (x-1) = 11 + 6(x-1)，则只要x-1为11的倍数，则5 + 6x可以被11整除，
• 5 + 6x 还可以转化为 5 + 12 + 6 * (x-2) = 17 + 6(x-2)，则只要x-2为17的倍数，则5 + 6x可以被17整除
• ......

6y+1，是基数为7，差值为6的等差数列，即 7 + 6x :

• 对于 7 + 6x 而言，如果x为7的倍数（7 * z），则7 + 6x = 7 + 6 * 7 * z = 7 *（1+6z）,则此时7 + 6x可以被7整除。
• 7 + 6x 还可以转化为 7 + 6 + 6 * (x-1) = 13 + 6(x-1)，则只要x-1为13的倍数，则7 + 6x可以被13整除，
• 7 + 6x 还可以转化为 7 + 12 + 6 * (x-2) = 19 + 6(x-2)，则只要x-2为19的倍数，则7 + 6x可以被19整除，
• ......

所以6y-1和6y+1可能整除的数自增量为6，这是for循环i自增为啥是 6的原因

且6y-1和6y+1的整除数基数为5和7，相差为2，这是for循环中素数判定的条件为啥是 n % i === 0 || n % (i+2) === 0的原因

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }
 
  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }
 
  return true;
}

此时时间复杂度为 O（sqrt(n) / 3） 

【相关推荐：javascript视频教程、编程基础视频】

Das obige ist der detaillierte Inhalt vonSo finden Sie Primzahlen in Javascript. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!