 Java
Java
 javaLernprogramm
javaLernprogramm
 Gängige Sortieralgorithmen für Java-Datenstrukturen (Zusammenfassungsfreigabe)
Gängige Sortieralgorithmen für Java-Datenstrukturen (Zusammenfassungsfreigabe)
Gängige Sortieralgorithmen für Java-Datenstrukturen (Zusammenfassungsfreigabe)
Dieser Artikel vermittelt Ihnen relevantes Wissen über Java und stellt hauptsächlich einige gängige Sortieralgorithmen vor, darunter direkte Einfügungssortierung, Hill-Sortierung (Reduzierung der inkrementellen Sortierung), Auswahlsortierung und Heap-Sortierung usw. Schauen wir uns das an, ich hoffe es wird für alle hilfreich sein.

1. Ordnung verstehen
Wenn wir in der Schule an einem Sporttreffen oder einer militärischen Ausbildung teilnehmen möchten, stellen wir uns von klein nach groß auf, wie zum Beispiel auf der Anwesenheitsliste, die der Lehrer im Unterricht hält , normalerweise Sie sind nach Studentenzahl von niedrig nach hoch sortiert. Ein weiteres Beispiel sind die Rankings der Programmiersprachen, die ebenfalls sortiert sind.
Es gibt eine ganze Reihe von Sortierszenarien im Leben. Es ist ersichtlich, dass das Sortieren immer noch sehr wichtig ist.
Das sogenannte Sortieren, nehmen Sie unser obiges Beispiel, ist der Vorgang des Sortierens in aufsteigender oder absteigender Reihenfolge nach der Größe eines oder mehrerer Schlüsselwörter. Dies ist das Sortieren, das auch die Stabilität des Sortierens beinhaltet, zum Beispiel:
Zum Beispiel gibt es einen Datensatz wie diesen: B D A C A F. Er muss nach seinen Ascll-Codes sortiert werden. Das erste A, das erscheint, nennen wir heißt A2.
Angenommen, das Ergebnis nach der Sortierung ist: A1 A2 B C D F, dann ist dieser Sortieralgorithmus stabil.
Angenommen, das Ergebnis nach der Sortierung lautet: A2 A1 B C D F, dann ist dieser Sortieralgorithmus instabil.
Kurz gesagt, wenn die zu sortierenden Daten zwei identische Elemente enthalten, hat sich die Beziehung zwischen den beiden Elementen nach Abschluss der Sortierung nicht geändert. Beispielsweise liegt A1 vor A2. Nach der Sortierung Noch vor A2 ist dies ein stabiler Sortieralgorithmus.
Hinweis: Ein instabiler Sortieralgorithmus ist von Natur aus instabil, aber ein stabiler Sortieralgorithmus kann so konzipiert werden, dass er instabil ist.
2. Klassifizierung der allgemeinen Sortierung
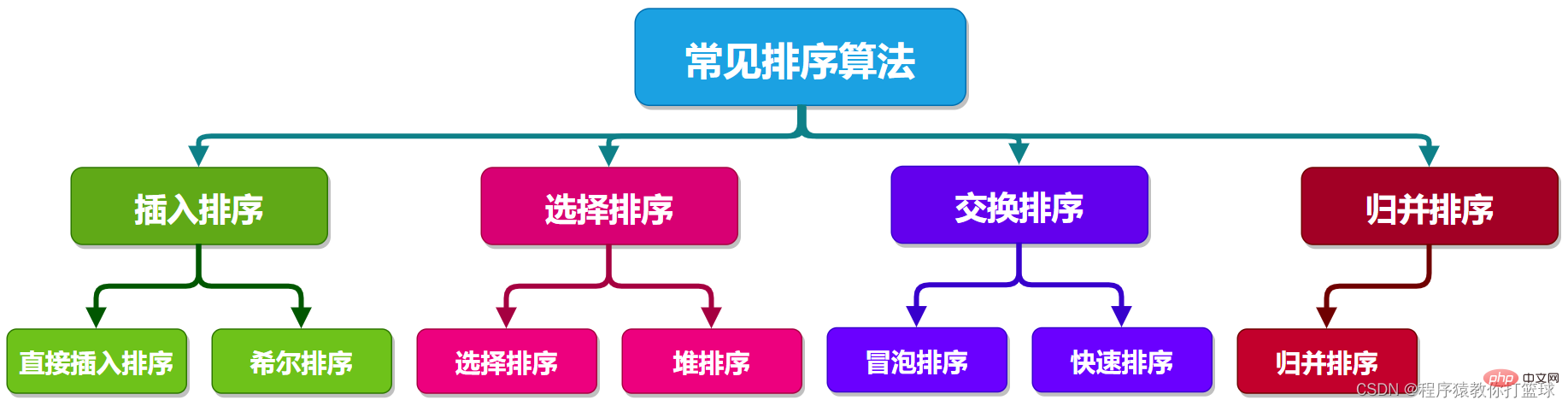
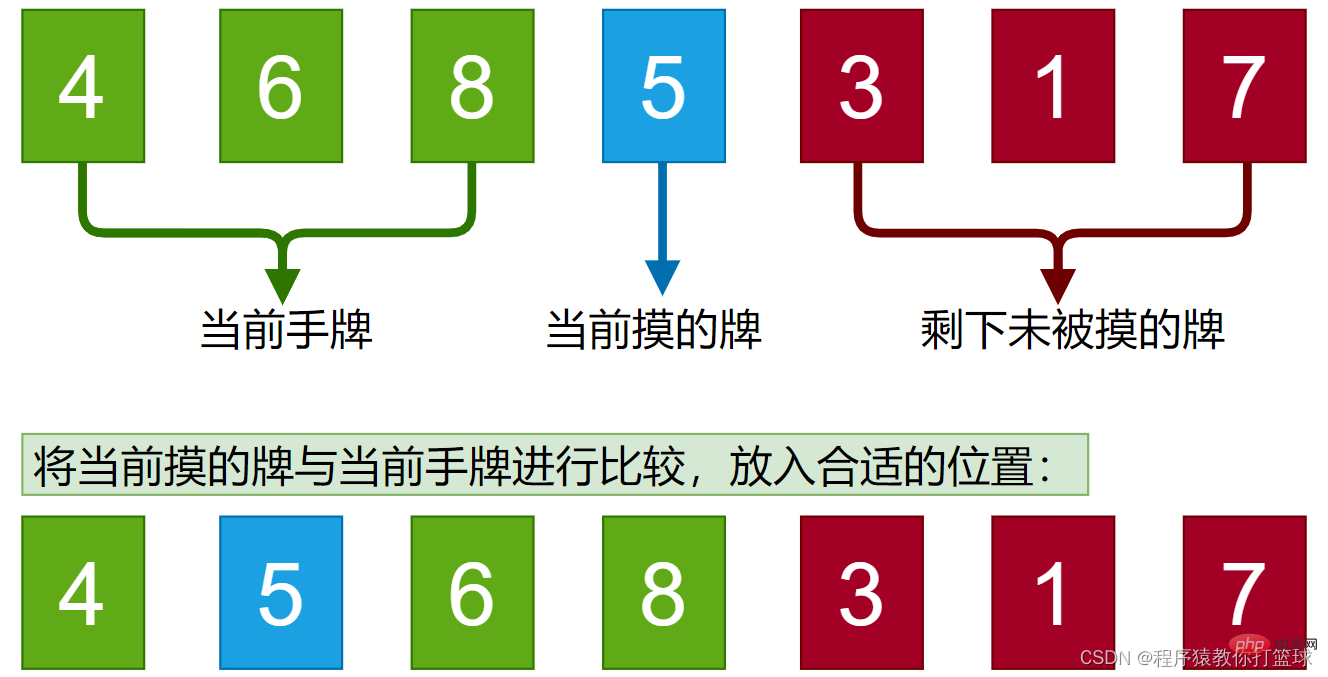
Dieses Bild fasst den Sortieralgorithmus zusammen, über den wir später sprechen und dann offiziell mit dem Studium dieses Kapitels beginnen werden! (Im Kapitel zum Sortieralgorithmus ist die Standardeinstellung aufsteigende Reihenfolge) Hinweis: Das später erwähnte Komplexitätsprotokoll basiert auf 2, und spezielle werden markiert. 3. Sortierung durch direktes Einfügen Vergleichen Sie die Karte auf der Hand und legen Sie sie an die entsprechende Stelle. Vergleichen Sie dann diese Karte mit den beiden Karten in Ihrer Hand und legen Sie sie an die entsprechende Stelle.
Dies ist eine direkte Einfügungssortierung. Die Elemente, die wir jedes Mal nehmen, werden in eine geordnete Reihenfolge eingefügt. Das heißt, bevor jede Karte gezogen wird, müssen wir sie nur vergleichen Kombiniert neu gezogene Karten mit den bestellten Karten auf der Hand und legt sie einfach an die entsprechende Position!Hier verwenden wir ein statisches Bild, um kurz zu demonstrieren:
Wir verstehen die allgemeine Idee bereits und müssen dann Code verwenden, um sie umzusetzen:
public void insertSort(int[] array) {
// 外循环控制趟数, 第一张牌默认有序, 所以 i 从 1 开始
for (int i = 1; i < array.length; i++) {
int tmp = array[i]; //当前摸到的牌
// 每次从手中牌的最后一张牌开始比较, 一直比到第一张牌
int j = i - 1;
for (; j >= 0; j--) {
//如果当前位置的牌,大于我摸到的牌,就往后挪
if (array[j] > tmp) {
array[j + 1] = array[j];
} else {
break;
}
}
// 把摸到的牌放到对应位置上
array[j + 1] = tmp;
}
}
Zeitkomplexitätsanalyse:
Das Äußere Die Schleife muss insgesamt n-1-mal verglichen werden, und im schlimmsten Fall muss die innere Schleife 1...n-mal verglichen werden. Entfernen Sie dann den kleinen Term vor n, d. h. (n-1) * n-mal. Das heißt, n^2 - n, entfernen Sie den Minimalterm und die endgültigeZeitkomplexität ist O(n^2)
- Raumkomplexitätsanalyse: öffnet einfach eine tmp-Variable i, j, also eine Konstante , Raumkomplexität Grad: O(1)
- Stabilität: Stabil
Je näher die Daten an der geordneten Situation dieser Sortierung liegen, desto höher ist die Zeiteffizienz.- 4. Hügelsortierung (Reduzierung der inkrementellen Sortierung)
- Diese Sortierung ist eine Optimierung der Direkteinfügungssortierung. Sie können sich vorstellen, dass vor Ihnen 8 Liebesnummernschilder platziert sind In der Reihenfolge müssen wir die Nummernschilder entsprechend den Anforderungen gruppieren. Nach der Gruppierung wird eine Gruppe mit 2 Nummernschildern durchgeführt durchgeführt wird und das dritte Intervall 1 Nummernschild als Gruppe umfasst, wird eine direkte Einfügungssortierung durchgeführt.
Es ist ein bisschen unklar, wann ich das gehört habe. Es spielt keine Rolle, was ich oben gesagt habe, indem ich Bilder zeichne:
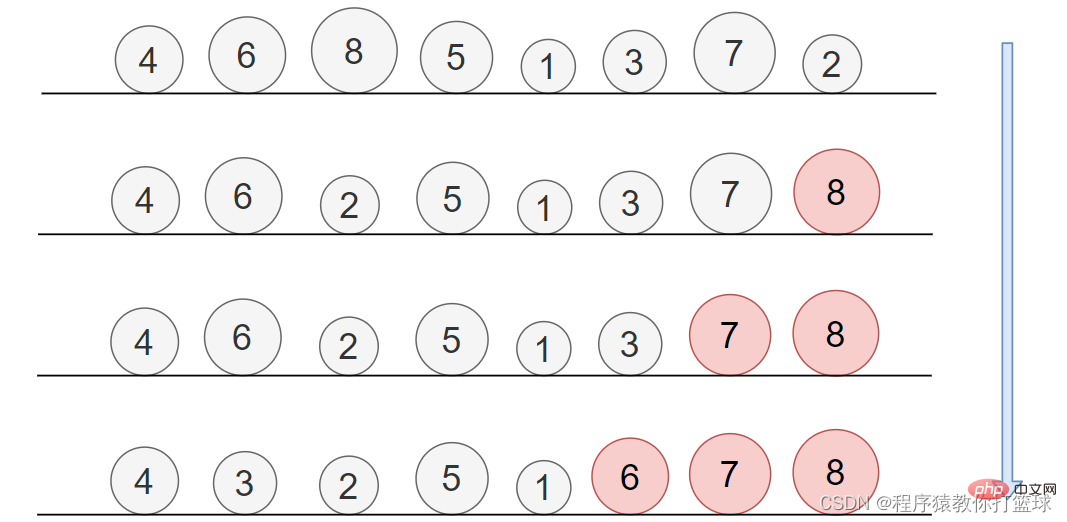
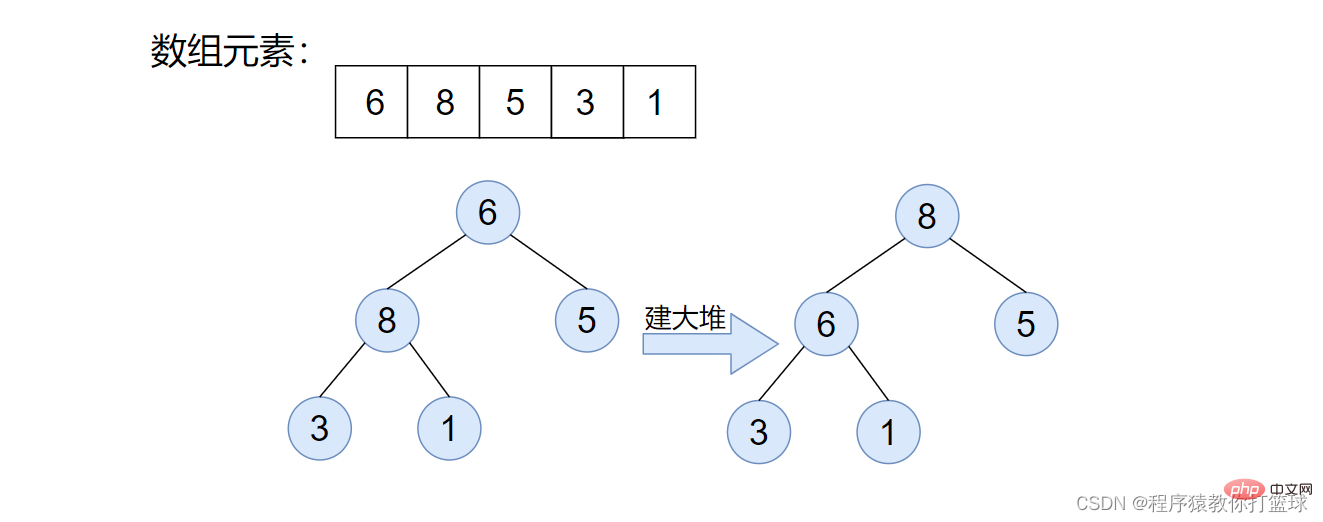
由上图我们可以发现,当间隔 > 1 的时候,都是预排序,也就是让我们的数据更接近有序,但是当间隔为 1 的时候,就是直接插入排序了,前面我们说过,直接插入排序,再数据接近有序的时候时间效率是很快的。由此可见,希尔排序,是直接插入排序的优化版。 如何在代码中实现呢?间隔的值如何取呢?代码中把这个间隔的值称为 gap,这个 gap 的取值方法有很多,有的人提出 gap 为奇数好,有的提出 gap 为偶数好,我们就采取一种比较简单的方法来取 gap 值,首次取数组长度一半的值为 gap,后续 gap /= 2,即可。当 gap 为 1,也就是直接插入排序了。 代码实现如下: 如果实在是不好理解,就结合上边讲的直接插入排序来理解,相信你能理解到的。 这个排序是个很简单的排序,你想象一下,有个小屁孩,喜欢玩小球,我给他安排了个任务,把这一排小球从小到大排列起来,摆给我看,于是小屁孩就找,每次从一排小球中找出最大的,放到最后,固定不动,那是不是也就是说,每次能确定一个最大的石子的最终位置了。我们来看图: 通过图片我们也能看出来,每次找到最大值于最后一个值交换,所以每趟都能把最大的放到最后固定不动,每趟能排序一个元素出来,那这样用代码来实现就很简单了: 这个算法有没有可以优化的空间呢? 有!那么既然小屁孩能一次找出最大的球,那能不能让小屁孩一次找出两个球出来呢?分别是这些球中,最大的和最小的,最大的放在最右边,最小的放在最左边,那么我们每次就能确定两个球的最终位置,也就是我们一次能排序两个元素。图解: 代码实现如下: 如果你有学习过优先级队列,或者看过博主优先级队列的文章,那么这个排序对于你来说还是很轻松的,当然在堆排序的讲解中,不会过多的去介绍堆的概念,如果对这部分概念还不理解,可以移至博主的上一篇文章进行学习。 堆排序,简单来说,就是把一组数据,看成一个完全二叉树,再把这棵树,建大堆或者建小堆,接着进行排序的一种思路。至于如何建大堆或小堆,和向上调整算法以及向下调整算法,这里也不多介绍了,博主的上篇文章都详细介绍过。 这里我们来分析一下,排升序应该建什么堆?大堆!排降序建小堆! 这里我们来排升序,建大堆,因为大堆堆顶元素一定是堆中最大的,所以我们可以把堆顶元素和最后一个元素进行交换,这样我们就确认了最大值的位置,接着将交换后的堆顶元素进行向下调整,仍然使得该数组满足大堆的特性!图解如下: 如上图步骤也很简单,先是将数组建成大堆,然后利用大堆来进行堆排序,首先将堆顶元素和最后一个元素交换,由此最大的元素就有序了,接着将该堆进行向下调整,使继续满足大堆性质,依次进行下去即可。 代码实现:public void shellSort(int[] array) {
// gap初始值设置成数组长度的一半
int gap = array.length >> 1;
// gap 为 1 的时候直接插入排序
while (gap >= 1) {
shell(array, gap);
gap >>= 1; // 更新 gap 值 等价于 -> gap /= 2;
}
}
private void shell(int[] array, int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i - gap;
for (; j >= 0; j -= gap) {
if (array[j] > tmp) {
array[j + gap] = array[j];
} else {
break;
}
}
array[j + gap] = tmp;
}
}
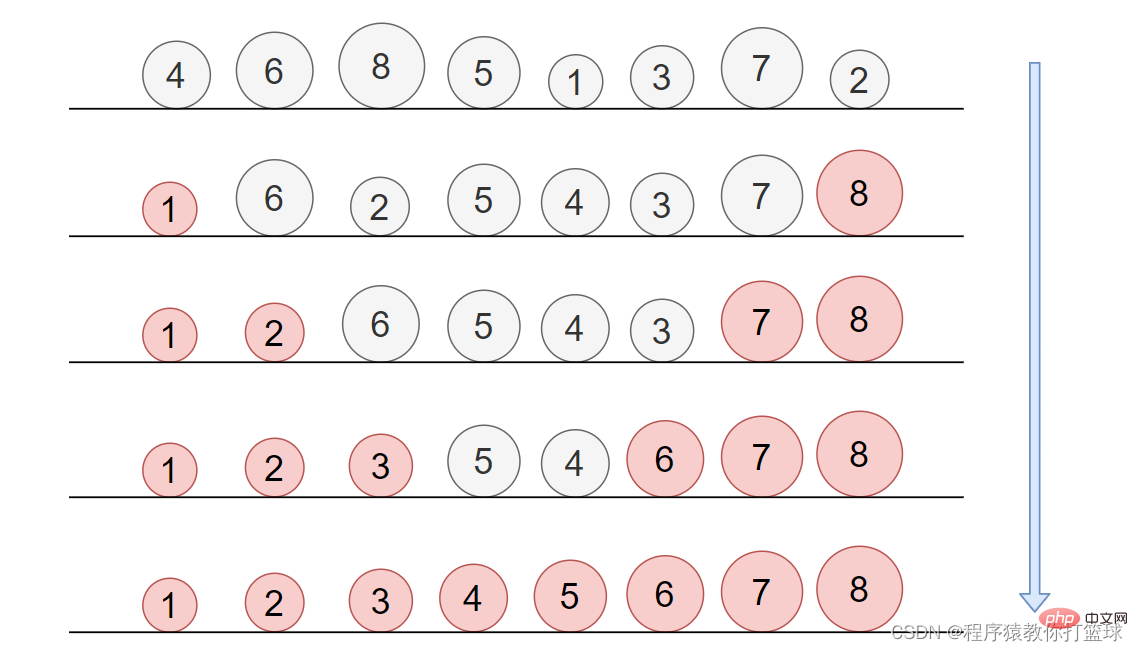
5、选择排序
public void selectSort(int[] array) {
int end = array.length - 1;
// 剩最后一个元素的时候, 不用比较了, 已经有序了
// 所以 i < array.length - 1
for (int i = 0; i < array.length - 1; i++) {
int max = 0;
int j = 0;
while (j <= end) {
if (array[j] > array[max]) {
max = j;
}
j++;
}
//找到了最大值的下标, 把最大值与最后一个值交换
swap(array, max, end--); // end-- 最后一个元素固定了, 不用参与比较
}
}
public void selectSort(int[] array) {
int left = 0;
int right = array.length - 1;
while (left < right) {
int maxIndex = left;
int minIndex = left;
// i = left + 1 -> 每次找最大最小值下标的时候, 可以不用算默认给的最大值和最小值下标
for (int i = left + 1; i <= right; i++) {
if (array[i] > array[maxIndex]) {
maxIndex = i;
}
if (array[i] < array[minIndex]) {
minIndex = i;
}
}
swap(array, minIndex, left);
// 如果最大值为 left 的位置情况的话, 走到这, 最大值已经被交换到 min 位置上了
if (maxIndex == left) {
// 更新最大值的位置
maxIndex = minIndex;
}
swap(array, maxIndex, right);
left++;
right--;
}
}6、堆排序
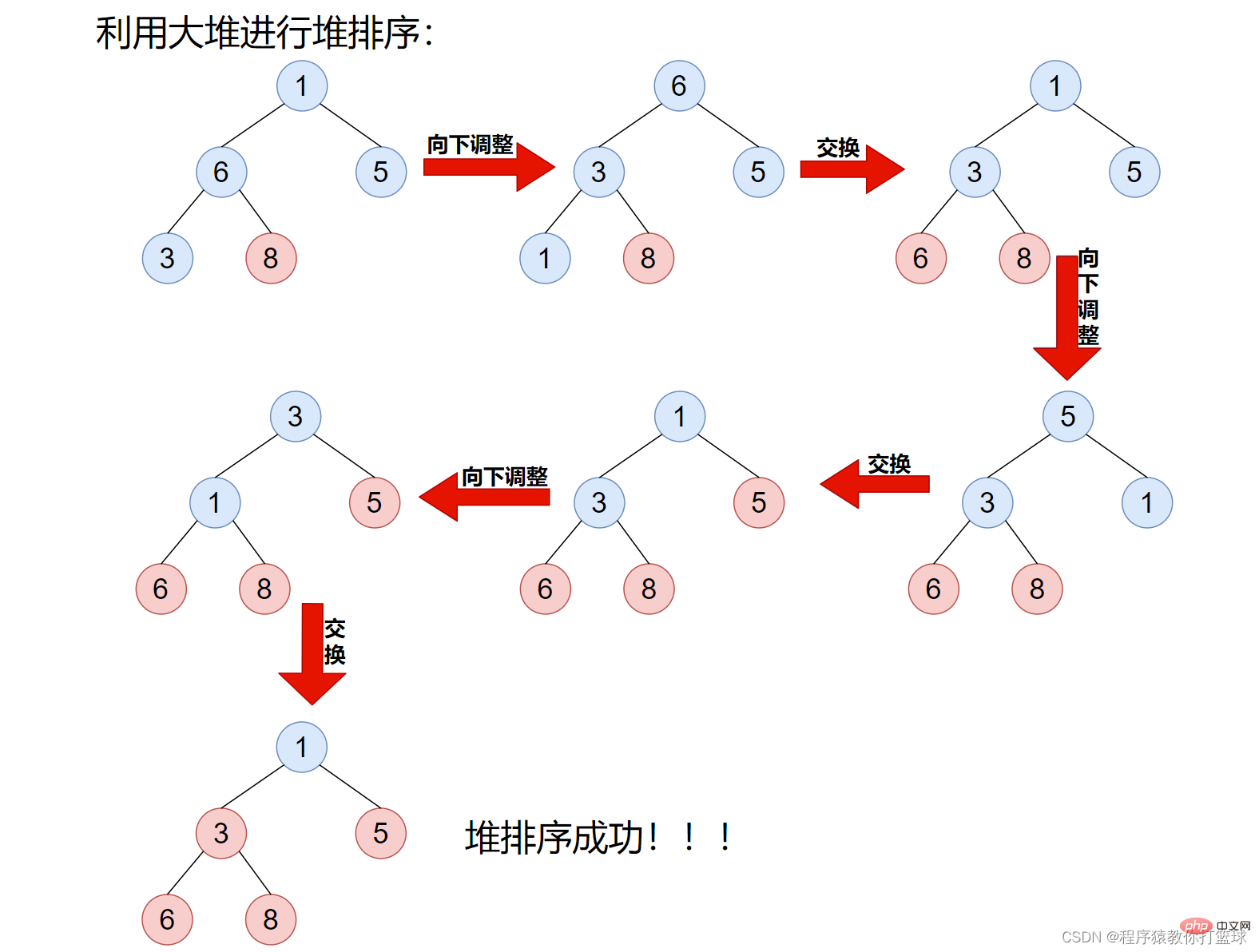
public void heapSort(int[] array) {
// 建大堆 从最后一个非叶子节点开始向下调整
// 非叶子节点下标 = (孩子节点下标 - 1) / 2
for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {
shiftDown(array, parent, array.length);
}
// 建大堆完成后, 每次堆顶元素与最后一个元素交换, 锁定最大元素的位置
for (int len = array.length - 1; len > 0; len--) {
swap(array, 0, len); //根节点与最后一个元素交换
shiftDown(array, 0, len); //根节点位置向下调整
}
}
private void shiftDown(int[] array, int parent, int len) {
int child = parent * 2 + 1;
while (child < len) {
if (child + 1 < len && array[child + 1] > array[child]) {
child++;
}
// 判断父节点是否大于较大的孩子节点
if (array[parent] < array[child]) {
swap(array, parent, child);
// 更新下标的位置
parent = child;
child = parent * 2 + 1;
} else {
return;
}
}
}
推荐学习:《java视频教程》
Das obige ist der detaillierte Inhalt vonGängige Sortieralgorithmen für Java-Datenstrukturen (Zusammenfassungsfreigabe). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1382
1382
 52
52
 Perfekte Zahl in Java
Aug 30, 2024 pm 04:28 PM
Perfekte Zahl in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur perfekten Zahl in Java. Hier besprechen wir die Definition, Wie prüft man die perfekte Zahl in Java?, Beispiele mit Code-Implementierung.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden für Weka in Java. Hier besprechen wir die Einführung, die Verwendung von Weka Java, die Art der Plattform und die Vorteile anhand von Beispielen.
 Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur Smith-Zahl in Java. Hier besprechen wir die Definition: Wie überprüft man die Smith-Nummer in Java? Beispiel mit Code-Implementierung.
 Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
In diesem Artikel haben wir die am häufigsten gestellten Fragen zu Java Spring-Interviews mit ihren detaillierten Antworten zusammengestellt. Damit Sie das Interview knacken können.
 Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Java 8 führt die Stream -API ein und bietet eine leistungsstarke und ausdrucksstarke Möglichkeit, Datensammlungen zu verarbeiten. Eine häufige Frage bei der Verwendung von Stream lautet jedoch: Wie kann man von einem Foreach -Betrieb brechen oder zurückkehren? Herkömmliche Schleifen ermöglichen eine frühzeitige Unterbrechung oder Rückkehr, aber die Stream's foreach -Methode unterstützt diese Methode nicht direkt. In diesem Artikel werden die Gründe erläutert und alternative Methoden zur Implementierung vorzeitiger Beendigung in Strahlverarbeitungssystemen erforscht. Weitere Lektüre: Java Stream API -Verbesserungen Stream foreach verstehen Die Foreach -Methode ist ein Terminalbetrieb, der einen Vorgang für jedes Element im Stream ausführt. Seine Designabsicht ist
 Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Anleitung zum TimeStamp to Date in Java. Hier diskutieren wir auch die Einführung und wie man Zeitstempel in Java in ein Datum konvertiert, zusammen mit Beispielen.
 Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Kapseln sind dreidimensionale geometrische Figuren, die aus einem Zylinder und einer Hemisphäre an beiden Enden bestehen. Das Volumen der Kapsel kann berechnet werden, indem das Volumen des Zylinders und das Volumen der Hemisphäre an beiden Enden hinzugefügt werden. In diesem Tutorial wird erörtert, wie das Volumen einer bestimmten Kapsel in Java mit verschiedenen Methoden berechnet wird. Kapselvolumenformel Die Formel für das Kapselvolumen lautet wie folgt: Kapselvolumen = zylindrisches Volumenvolumen Zwei Hemisphäre Volumen In, R: Der Radius der Hemisphäre. H: Die Höhe des Zylinders (ohne die Hemisphäre). Beispiel 1 eingeben Radius = 5 Einheiten Höhe = 10 Einheiten Ausgabe Volumen = 1570,8 Kubikeinheiten erklären Berechnen Sie das Volumen mithilfe der Formel: Volumen = π × R2 × H (4
 Wie führe ich Ihre erste Spring -Boot -Anwendung in der Spring Tool Suite aus?
Feb 07, 2025 pm 12:11 PM
Wie führe ich Ihre erste Spring -Boot -Anwendung in der Spring Tool Suite aus?
Feb 07, 2025 pm 12:11 PM
Spring Boot vereinfacht die Schaffung robuster, skalierbarer und produktionsbereiteter Java-Anwendungen, wodurch die Java-Entwicklung revolutioniert wird. Der Ansatz "Übereinkommen über Konfiguration", der dem Feder -Ökosystem inhärent ist, minimiert das manuelle Setup, Allo



