 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 CMU Zhang Kun: Neueste Fortschritte in der Kausaldarstellungstechnologie
CMU Zhang Kun: Neueste Fortschritte in der Kausaldarstellungstechnologie
CMU Zhang Kun: Neueste Fortschritte in der Kausaldarstellungstechnologie

1. Warum sollte man sich um Kausalität kümmern
Lassen Sie uns zunächst vorstellen, was Kausalität ist:
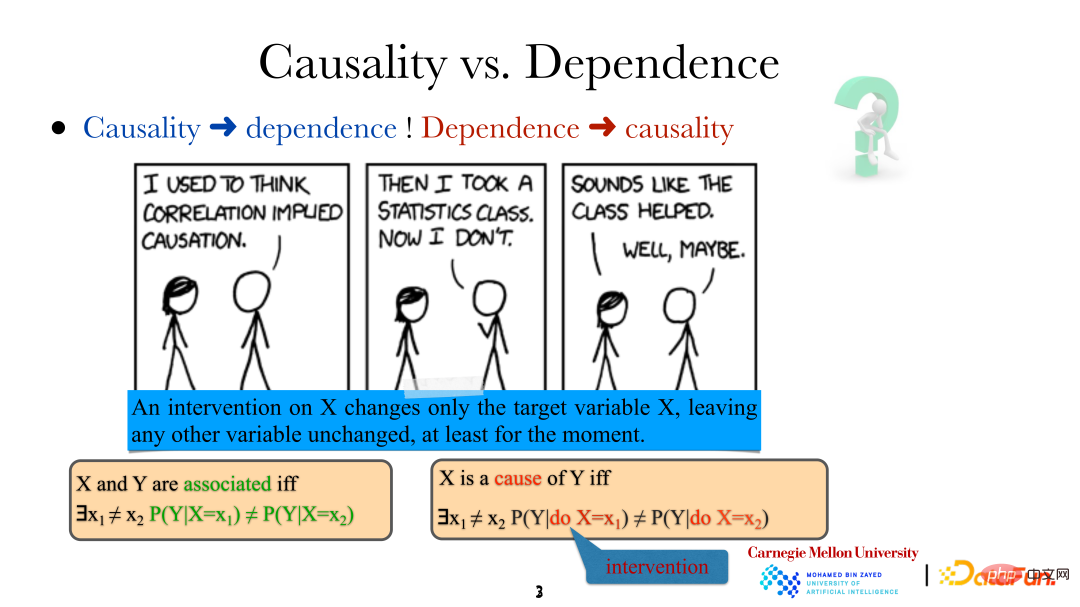
Wenn wir sagen, dass Variablen/Ereignisse zusammenhängen, bedeutet das, dass sie nicht unabhängig sind, also nicht unabhängig. Es muss eine Beziehung bestehen. Allerdings bedeutet X als „Ursache“ von Y, dass sich Y (der Boden wird nass) entsprechend ändert, wenn eine bestimmte Methode verwendet wird, um X (es regnet) zu ändern, d durchgeführt am Nicht dasselbe. Es ist zu beachten, dass der Eingriff hier nicht zufällig erfolgt, sondern eine sehr präzise direkte Steuerung der Zielvariablen (direkte Änderung von „es regnet“). Diese Änderung hat keine direkten Auswirkungen auf andere Variablen im System. Gleichzeitig können wir auf diese Weise, also durch direktes menschliches Eingreifen, auch feststellen, ob eine Variable die direkte Ursache einer anderen Variable ist.
Das Folgende ist ein Beispiel für die Notwendigkeit, kausale Zusammenhänge zu analysieren:
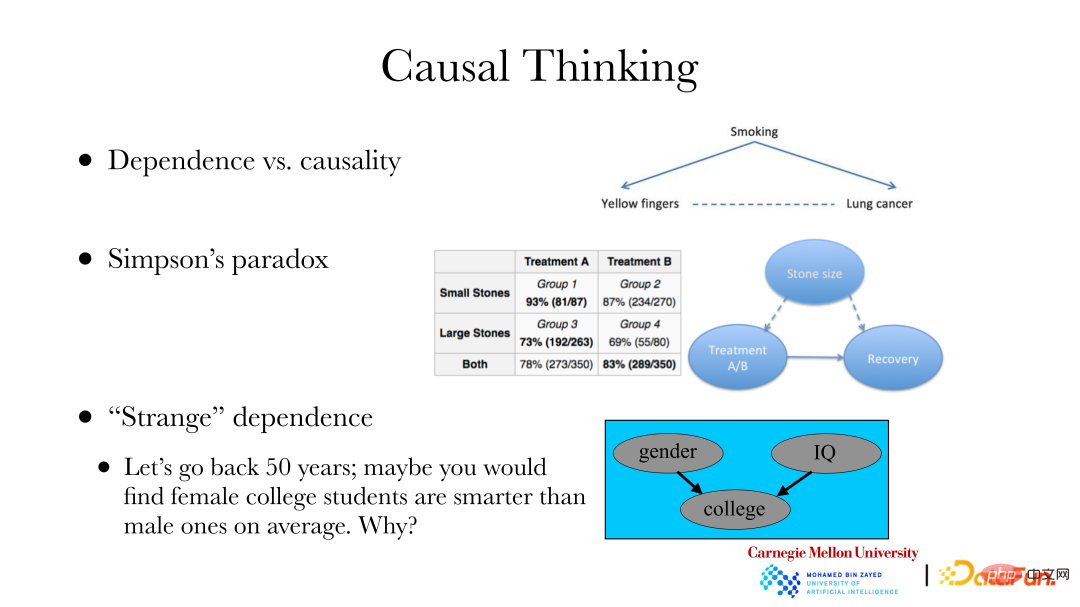
① Ein klassischer Fall ist: Es gibt einen Zusammenhang zwischen Lungenerkrankungen und Nagelfarbe durch Rauchen, das heißt, weil Zigaretten keine Filter haben, normal Rauchen führt zu Gelbfärbung der Fingernägel, Rauchen kann auch Lungenerkrankungen verursachen. Wenn Sie das Auftreten von Lungenerkrankungen in einem bestimmten Bereich ändern möchten, kann dies nicht durch das Bleichen Ihrer Nägel verbessert werden. Sie müssen die Ursache der Lungenerkrankung finden, anstatt die Abhängigkeit der Lungenerkrankung zu ändern. Um das Ziel zu erreichen, die Inzidenz von Lungenerkrankungen zu verändern, ist eine Ursachenanalyse erforderlich.
② Der zweite Fall ist: Simpsons Paradoxon. Die rechte Seite des Bildes oben ist ein echter Datensatz. Der Datensatz zeigt zwei Sätze von Nierensteindaten, eine Gruppe enthält kleinere Steine und die andere enthält auch größere Steine. Es gibt auch zwei Behandlungsmethoden A und B. Aus der Tabelle geht hervor, dass unabhängig von der Gruppe der kleinen oder großen Steine die Ergebnisse der Behandlungsmethode A mit Heilungsraten von 93 % bzw. 73 % besser sind und die Heilungsraten der Behandlungsmethode B besser sind 87 % bzw. 69 %. Wenn jedoch zwei Gruppen von Steinpatienten mit derselben Behandlungsmethode gemischt wurden, war die Gesamtwirkung von Behandlungsplan B (83 %) besser als die von Behandlungsplan A (78 %). Angenommen, Sie sind ein Arzt, der sich nur um die Heilungsrate und die Auswahl eines Behandlungsplans für neue Patienten kümmert. Der Grund dafür ist, dass wir uns bei der Abgabe von Empfehlungen nur um den kausalen Zusammenhang zwischen Behandlung und Heilung kümmern und uns nicht um andere Abhängigkeiten kümmern. Allerdings ist die Steingröße eine häufige Ursache sowohl für die Behandlung als auch für die Heilung, was zu quantitativen Veränderungen in der Abhängigkeit von Behandlung und Heilung führt. Daher sollten wir bei der Untersuchung des Zusammenhangs zwischen Behandlungsmethoden und Heilung den Kausalzusammenhang zwischen ersteren und letzteren und nicht die Abhängigkeitsbeziehung diskutieren.
③ Der dritte Fall: Vor 50 Jahren zeigten Statistiken, dass Frauen an Hochschulen und Universitäten im Durchschnitt schlauer waren als Männer, aber in Wirklichkeit sollte es keinen signifikanten Unterschied geben. Es besteht ein Selektionsbias, da es für Frauen schwieriger ist, an einer Hochschule zu studieren als für Männer. Das heißt, dass Schulen bei der Rekrutierung von Studierenden von Faktoren wie Geschlecht und Prüfungsfähigkeiten beeinflusst werden. Wenn das „Ergebnis“ vorliegt, wird es einen Zusammenhang zwischen Geschlecht und Prüfungsfähigkeit geben. Das Problem des Selektionsbias besteht auch bei der Verwendung von im Internet gesammelten Daten. Es besteht häufig ein Zusammenhang zwischen der Erfassung eines Datenpunkts und bestimmten Attributen. Wenn Sie nur im Internet bereitgestellte Daten analysieren, müssen Sie auf diese Faktoren achten. Wenn dies erkannt wird, können Daten mit Selektionsverzerrung auch durch kausale Beziehungen analysiert werden, und dann kann die Natur der gesamten Gruppe selbst wiederhergestellt oder abgeleitet werden.

Das obige Bild zeigt mehrere Probleme des maschinellen Lernens/Deep Learnings:
① Wir wissen, dass es einen Zusammenhang zwischen der besten Vorhersage und der Verteilung der Daten gibt. Will man beim Transfer-Learning beispielsweise ein Modell von Afrika auf den amerikanischen Kontinent übertragen und trotzdem optimale Vorhersagen treffen, sind dafür natürlich adaptive Anpassungen des Modells auf Basis unterschiedlicher Datenverteilungen erforderlich. Zu diesem Zeitpunkt ist es besonders wichtig zu analysieren, welche Veränderungen in der Datenverteilung stattgefunden haben und wie diese sich verändert haben. Wenn Sie wissen, was sich an den Daten geändert hat, können Sie das Modell entsprechend anpassen. Ein weiteres Beispiel: Wenn Sie ein KI-Modell zur Diagnose einer Krankheit erstellen, werden Sie mit den von der Maschine vorgeschlagenen Diagnoseergebnissen nicht zufrieden sein. Sie möchten außerdem wissen, warum die Maschine zu diesem Schluss gekommen ist, beispielsweise welche Mutation die Krankheit verursacht hat. Darüber hinaus wirft die Behandlung einer Krankheit viele „Warum“-Fragen auf. Wenn ein Empfehlungssystem eine Empfehlung ausspricht, möchte es in ähnlicher Weise wissen, warum es diesen Artikel/diese Strategie empfiehlt, z. B. ob das Unternehmen nur den Umsatz steigern möchte oder ob der Artikel/die Strategie für den Benutzer oder der Artikel/die Strategie geeignet ist ist für die Zukunft von Vorteil. Diese „Warum“-Fragen sind alles Ursache-Wirkungs-Fragen.
② Im Bereich Deep Learning gibt es das Konzept der gegnerischen Angriffe. Wenn Sie, wie in der Abbildung gezeigt, dem Bild des Großen Pandas auf der linken Seite ein bestimmtes Rauschen hinzufügen oder bestimmte Pixel usw. ändern, beurteilt die Maschine das Bild als andere Tierarten anstelle von Riesenpandas, und das Vertrauensniveau beträgt immer noch sehr hoch. Für den Menschen handelt es sich bei diesen beiden Bildern jedoch offensichtlich um Riesenpandas. Dies liegt daran, dass die High-Level-Funktionen, die Maschinen derzeit aus Bildern lernen, nicht mit den High-Level-Funktionen übereinstimmen, die von Menschen gelernt werden. Wenn die von Maschinen verwendeten High-Level-Funktionen nicht mit denen von Menschen übereinstimmen, kann es zu gegnerischen Angriffen kommen. Wenn die Eingabe geändert wird, ändert sich die Beurteilung von Menschen oder Maschinen und es treten Probleme mit dem endgültigen Beurteilungsergebnis auf. Nur wenn der Maschine ermöglicht wird, High-Level-Funktionen zu lernen, die mit Menschen konsistent sind, d. h. die Maschine Funktionen auf die gleiche Weise wie Menschen lernen und nutzen kann, können gegnerische Angriffe vermieden werden.

Warum müssen wir eine kausale Darstellung durchführen?
① Nachgelagerte Aufgaben profitieren: Beispielsweise kann es dazu beitragen, dass nachgelagerte Aufgaben wie die Klassifizierung besser erledigt werden.
② Kann „Warum“-Fragen erklären.
③ Stellen Sie die tatsächlichen kausalen Merkmale hinter den Daten wieder her: Kants Metaphysik in der Philosophie glaubt, dass die vom Menschen erlebte Welt die empirische Welt ist. Obwohl sie auf der Welt an sich dahinter basiert, können wir die Weltontologie nicht direkt wahrnehmen. Einige Eigenschaften wie Zeit, Raum, kausale Ordnung usw. wurden durch das Sinnessystem automatisch zur Erfahrungswelt hinzugefügt. Wenn Sie also möchten, dass eine Maschine Merkmale lernt, die denen des Menschen entsprechen, muss die Maschine in der Lage sein, Merkmale wie kausale Reihenfolge/Beziehung, Zeit und Raum zu lernen.
2. Kausales Repräsentationslernen: unabhängige und identisch verteilte Situation
1 Grundkonzepte des kausalen Repräsentationslernens
Wie lernt man kausale Zusammenhänge in der unabhängigen und identisch verteilten Situation? Zunächst müssen zwei Fragen beantwortet werden: Erstens, welche Eigenschaften in den Daten mit der Kausalität zusammenhängen und welche Anhaltspunkte („Fußabdruck“) in den Daten vorhanden sind. Die zweite Frage ist, ob der Kausalzusammenhang unter den Bedingungen der Datenbeschaffung wiederhergestellt werden kann, also die Frage der Identifizierbarkeit des Kausalsystems.

Die wesentlichste Eigenschaft eines Kausalsystems ist „Modularität“: Obwohl Variablen im System bestimmte Beziehungen haben, kann das System basierend auf Kausalbeziehungen in mehrere Subsysteme unterteilt werden (eine Ursache erzeugt eine abhängige Variable). Beispielsweise sind „Es regnet“, „Der Boden ist nass“ und „Der Boden ist rutschig“ voneinander abhängig und können durch kausale Zusammenhänge in drei Subsysteme unterteilt werden: „Aus bestimmten Gründen regnet es“, „Es regnet.“ bewirken, dass der Boden nass wird.“ , „Der nasse Boden führt dazu, dass der Boden rutschig wird.“ Obwohl Abhängigkeiten zwischen Variablen bestehen, sind diese drei Prozesse (Prozesse, Subsysteme) nicht miteinander verbunden, es gibt keine gemeinsame Nutzung von Parametern und Änderungen in einem System führen nicht zu Änderungen im anderen System. Wenn beispielsweise bestimmte Substanzen versprüht werden, um den Effekt zu ändern, dass „nasser Boden rutschigen Boden verursacht“, hat dies keinen Einfluss darauf, ob es regnet oder nicht, und es ändert auch nicht die Wirkung von Regen auf nassen Boden. Diese Eigenschaft wird als „Modularität“ bezeichnet, was bedeutet, dass das System aus ursächlicher Sicht in verschiedene Untermodule unterteilt ist und keine Verbindung zwischen den Untermodulen besteht.
Ausgehend von der Modularität können wir drei Eigenschaften von Kausalsystemen erhalten:
① Bedingte Unabhängigkeit zwischen Variablen.
② Unabhängiger Geräuschzustand.
③ Minimale (und unabhängige) Änderungen.
In Bezug auf die Identifizierbarkeit von Kausalsystemen schenkt maschinelles Lernen selbst der Frage der Identifizierbarkeit nicht viel Aufmerksamkeit. Beispielsweise muss das Vorhersagemodell beurteilen, ob das Vorhersageergebnis genau oder optimal ist, aber es gibt keine „Wahrheit“. „zu urteilen. Bei der Kausalanalyse/kausalen Repräsentation geht es jedoch darum, die „Wahrheit“ der Daten wiederherzustellen, das heißt, es wird mehr darauf geachtet, ob die kausale Natur hinter den Daten identifiziert werden kann.
Zwei grundlegende Konzepte werden im Folgenden vorgestellt:
① Kausale Entdeckung: Erforschung der zugrunde liegenden Kausalstruktur/des zugrunde liegenden Kausalmodells anhand von Daten.
② Lernen der Kausaldarstellung: Finden Sie die zugrunde liegenden versteckten Variablen auf hoher Ebene und Beziehungen zwischen Variablen aus direkt beobachteten Daten.
2. Einteilung des Kausalrepräsentationslernens
Kausalrepräsentationslernmethoden werden im Allgemeinen aus den folgenden drei Perspektiven unterteilt:
① Dateneigenschaften: ob sie unabhängig und identisch verteilt sind („i.i.d.-Daten“). Zu den nicht unabhängigen und identisch verteilten Daten gehören nicht unabhängige, aber identisch verteilte Daten, beispielsweise identisch verteilte Daten mit Zeitabhängigkeit (z. B. Zeitreihendaten), oder unabhängige, aber unterschiedlich verteilte Daten, z. B. Datenverteilungsänderungen (oder eine Kombination dieser beiden). derer).
② Parameterbeschränkungen („Parameterbeschränkungen“): Gibt es weitere zusätzliche Eigenschaften für die Auswirkung der Kausalität, wie z. B. parametrische Modelle?
③ Potenzielle Störfaktoren („latente Störfaktoren“): Ob die Existenz unbeobachteter gemeinsamer Faktoren oder Störfaktoren im System zugelassen werden soll.
Die folgende Abbildung zeigt detailliert die spezifischen Ergebnisse, die unter verschiedenen Einstellungen erzielt werden können:

Zum Beispiel bei unabhängiger und identischer Verteilung, wenn keine Parametermodellbeschränkungen vorliegen, unabhängig davon, ob Potenzial vorhanden ist Störfaktoren usw. können im Allgemeinen erhalten werden. Wenn parametrische Modellbeschränkungen vorliegen, kann die Wahrheit dahinter im Allgemeinen direkt wiederhergestellt werden.
3. Unabhängiges und identisch verteiltes Kausalrepräsentationslernen

Die obige Abbildung zeigt ein Beispiel ohne Parametermodellbeschränkungen im unabhängigen und identisch verteilten Fall. Die Daten zeigen insgesamt 8 Messvariablen für 250 Schädel, darunter Geschlecht, Standort, Wetter sowie Schädelgröße und -form. Archäologen möchten wissen, was das unterschiedliche Aussehen von Menschen in verschiedenen Gebieten verursacht. Wenn wir diesen Kausalzusammenhang kennen, können wir möglicherweise das Aussehen von Menschen anhand von Veränderungen in der Umgebung und anderen Faktoren vorhersagen. Offensichtlich kann unter solchen Bedingungen kein menschlicher Eingriff durchgeführt werden. Selbst wenn ein Eingriff hinzugefügt wird, wird die Beobachtung der Ergebnisse lange dauern, sodass der kausale Zusammenhang nur aus den vorhandenen Beobachtungsdaten ermittelt werden kann.
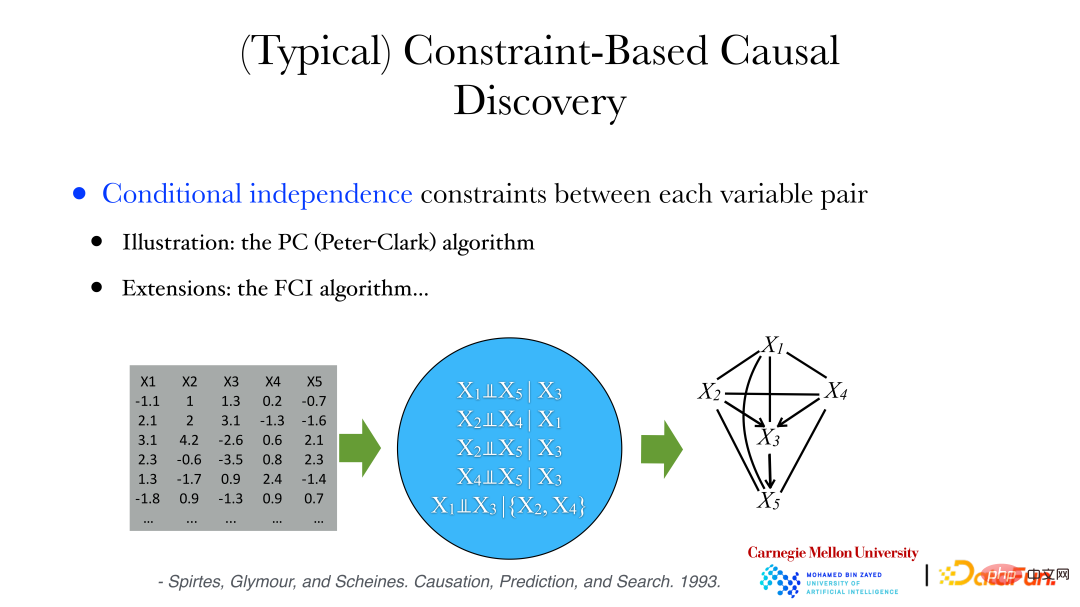
Wie in der Abbildung oben gezeigt, ist die Beziehung zwischen Variablen sehr komplex, sie kann linear oder nichtlinear sein und die Variablendimensionen können auch inkonsistent sein. Wenn das Geschlecht eine Dimension hat, können die Schädelmerkmale 255 Dimensionen haben. Zu diesem Zeitpunkt kann die Eigenschaft der bedingten Unabhängigkeit genutzt werden, um kausale Zusammenhänge zu konstruieren.
Zu den Methoden gehören die folgenden zwei:
① PC-Algorithmus (Peter-Clark): Der Algorithmus geht davon aus, dass im System keine gemeinsamen Faktoren beobachtet werden.
② FCI-Algorithmus: wird verwendet, wenn versteckte Variablen vorhanden sind.
Im Folgenden wird der PC-Algorithmus zur Analyse archäologischer Daten verwendet: Aus den Daten kann eine Reihe bedingt unabhängiger Eigenschaften abgeleitet werden, z. B. dass die Variablen X1 und X5 bedingt unabhängig sind, wenn X3 angegeben ist usw. Gleichzeitig können wir beweisen, dass es keine Kante zwischen zwei Variablen gibt, wenn sie bedingt unabhängig sind. Wenn die Variablen bedingt unabhängig sind, können wir dann die verbundenen Kanten entfernen, um einen ungerichteten Graphen zu erhalten. Anschließend können wir die Richtung der Kanten im Graphen ermitteln Graph) oder eine Sammlung gerichteter azyklischer Graphen, um die bedingten Unabhängigkeitsbeschränkungen zwischen Variablen in den Daten zu erfüllen.
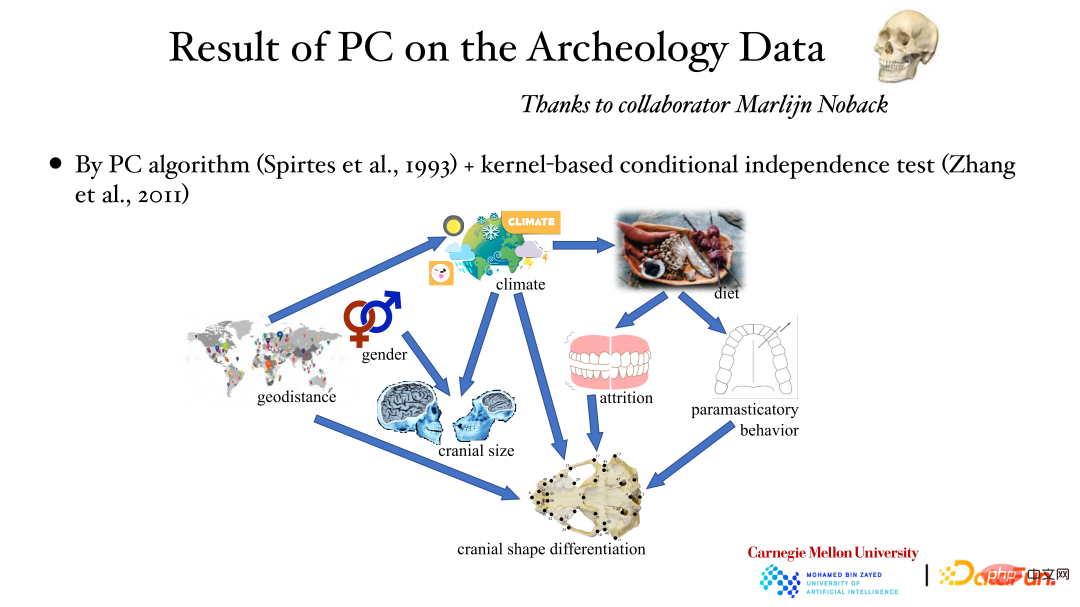
Die obige Abbildung zeigt die Ergebnisse der Analyse archäologischer Daten mithilfe des PC-Algorithmus und der bedingten Unabhängigkeitstestmethode des Kernels: Der geografische Standort beeinflusst das Wetter, das Wetter beeinflusst die Schädelgröße und das Geschlecht beeinflusst auch die Schädelgröße usw. Der kausale Zusammenhang dahinter wurde durch Datenanalyse ermittelt.
Eines der beiden gerade erwähnten Probleme besteht darin, die Richtung jeder Kante der Variablen DAG zu ermitteln, was zusätzliche Annahmen erfordert. Wenn Sie einige Annahmen darüber treffen, wie Ursache die Wirkung beeinflusst, werden Sie feststellen, dass Ursache und Wirkung asymmetrisch sind, sodass Sie die Richtung von Ursache und Wirkung herausfinden können. Der Datenhintergrund in der folgenden Abbildung besteht immer noch aus unabhängigen und identisch verteilten Daten, und es wurden zusätzliche Parameterbeschränkungen hinzugefügt, und Störfaktoren sind im System immer noch nicht zulässig. Derzeit können die folgenden drei Arten von Modellen verwendet werden, um die Richtung der Kausalität zu untersuchen:
① Lineares nicht-Gaußsches Modell;
② Post-nichtlineares Kausalmodell (PNL, Post-nichtlineares Kausalmodell);
③ Additives Geräuschmodell (ANM, Additives Geräuschmodell).
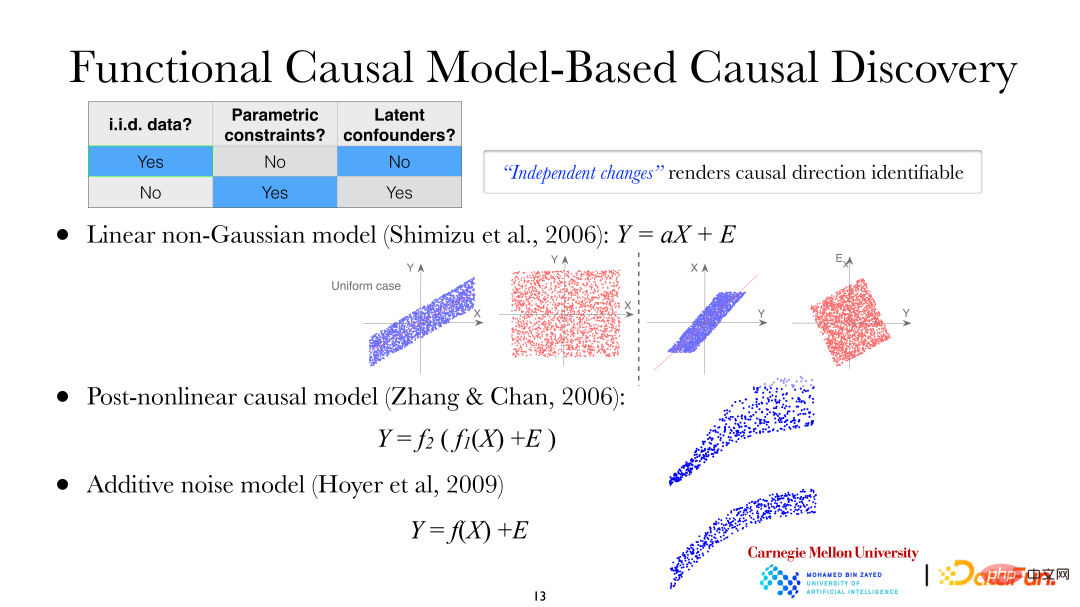
Im linearen nicht-Gaußschen Modell wird angenommen, dass X zu Y führt, das heißt, X ist die abhängige Variable und Y die Effektvariable. Aus der Abbildung ist ersichtlich, dass bei Verwendung von X zur Erklärung von Y für die lineare Regression die Residuen und Aber in diesem Moment ist das Modell linear, nicht-Gauß-basiert, das heißt, unkorreliert bedeutet nicht, dass sie unabhängig sind. Es kann festgestellt werden, dass eine Asymmetrie zwischen der abhängigen Variablen und der Effektvariablen besteht. Gleiches gilt für post-nichtlineare Kausalmodelle und additive Rauschmodelle.

Die obige Abbildung zeigt das post-nichtlineare Kausalmodell: Die zweite nichtlineare Funktion (f2) außerhalb wird im Allgemeinen verwendet, um nichtlineare Änderungen zu beschreiben, die während des Messprozesses im System eingeführt werden, häufig beim Beobachten/Messen von Daten Es wird keine geben -lineare Änderungen. Beispielsweise wird es im biologischen Bereich zusätzliche nichtlineare Veränderungen geben, wenn Instrumente zur Messung von Genexpressionsdaten verwendet werden. Lineare Modelle, nichtlineare additive Rauschmodelle und multiplikative Rauschmodelle sind allesamt Sonderfälle von PNL-Modellen.
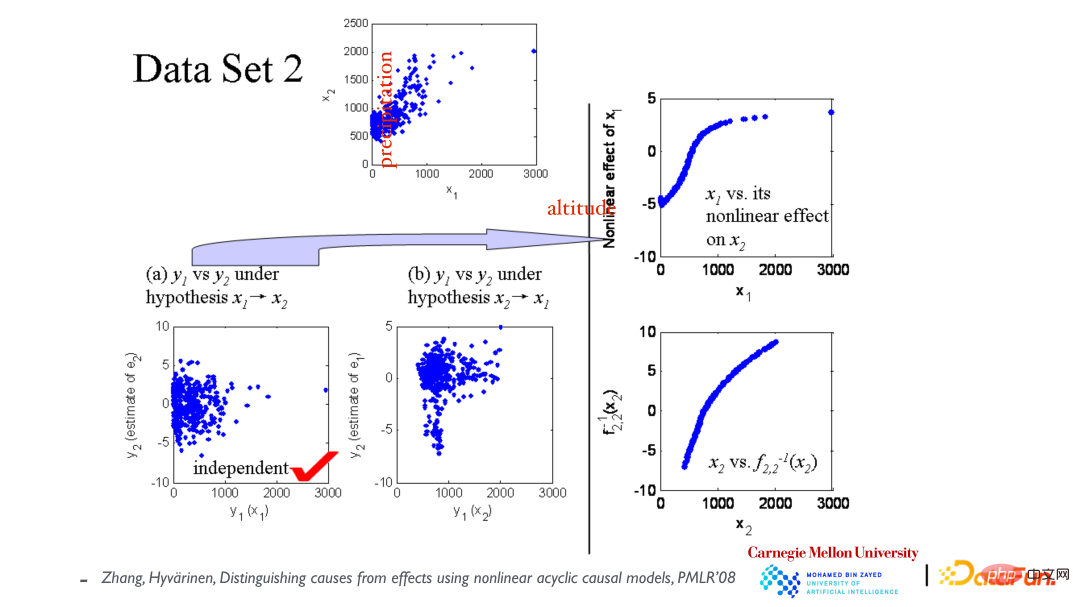
Das obere Streudiagramm zeigt die Beziehung zwischen den Variablen x1 (Höhe) und x2 (jährlicher Niederschlag). Nehmen Sie zunächst an, dass x1 x2 verursacht, und erstellen Sie dann ein Modell, das an die Daten angepasst ist. Wie in der unteren linken Ecke gezeigt, sind die Residuen und x1 unabhängig. Nehmen Sie dann an, dass x2 x1 verursacht, und passen Sie das Modell erneut an und x2 sind nicht unabhängig (siehe mittleres Bild). Daraus wird geschlossen, dass die kausale Richtung dadurch verursacht wird, dass x1 zu x2 führt.

Die Asymmetrie der Kausalvariablen lässt sich zwar aus dem vorherigen Beispiel ermitteln, aber kann dieses Ergebnis theoretisch garantiert werden? Und es ist das einzig richtige Ergebnis. Die entgegengesetzte Richtung (Wirkung zur Ursache) kann die Daten nicht erklären? Der Beweis ist in der obigen Tabelle dargestellt. In fünf Fällen können die Daten in beide Richtungen erklärt werden (Ursache zu Wirkung, Wirkung zu Ursache). Das erste ist das lineare Gaußsche Modell, bei dem die Beziehung linear ist und die Verteilung eine Gaußsche Verteilung ist, bei der die kausale Asymmetrie verschwindet. Die anderen vier sind Sondermodelle.

Auch wenn die Daten mit einem post-nichtlinearen Modell analysiert werden, können Ursache und Wirkung unterschieden werden. Unabhängige Residuen können in der richtigen Richtung gefunden werden, jedoch nicht in der entgegengesetzten Richtung. Da sowohl das lineare Modell als auch das nichtlineare additive Rauschmodell Sonderfälle des post-nichtlinearen Modells sind, sind beide Modelle auch in diesem Fall anwendbar und können die kausale Richtung finden.
Bei zwei Variablen kann ihre kausale Richtung mit der oben beschriebenen Methode ermittelt werden. In weiteren Fällen müssen jedoch die folgenden Probleme gelöst werden: Beispielsweise werden im Bereich der Psychologie Antworten auf einige Fragen (xi) über Fragebögen gesammelt. Zwischen diesen Antworten besteht eine Abhängigkeit, und es wird nicht davon ausgegangen, dass eine solche besteht ein Zusammenhang zwischen diesen Antworten.
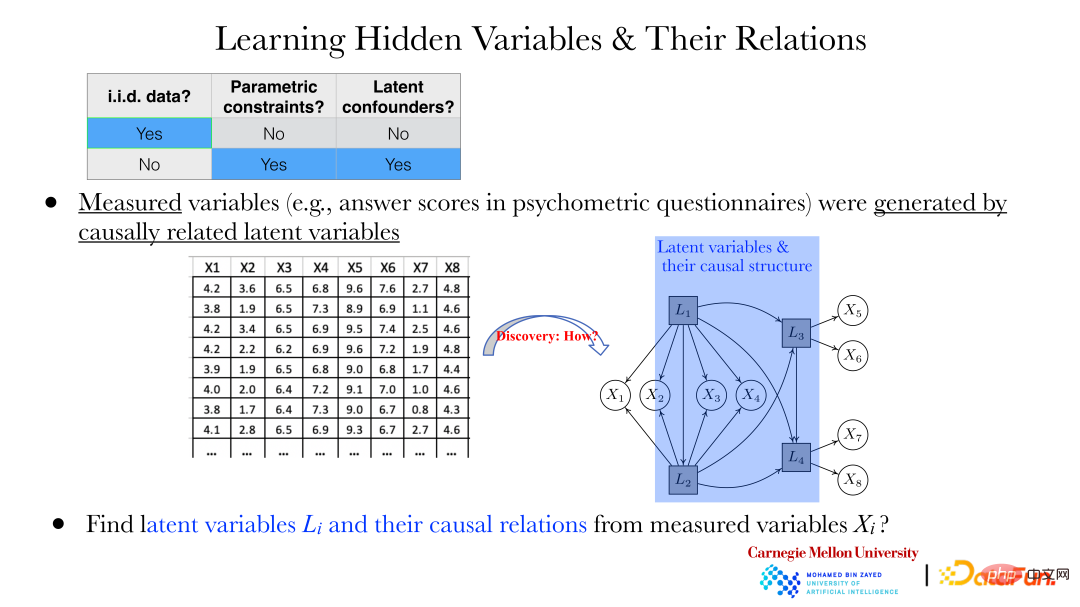
Aber wie in der Abbildung oben gezeigt, werden diese xi durch die versteckten Variablen Li dahinter generiert. Besonders wichtig ist es, die verborgenen Variablen Li und die Beziehung zwischen verborgenen Variablen durch das beobachtete xi aufzudecken.

In den letzten Jahren gab es einige Methoden, die uns helfen können, diese abhängigen Variablen und ihre Beziehungen zu finden. Die obige Abbildung zeigt ein Anwendungsbeispiel der Generalized Independent Noise (GIN)-Methode, mit der eine Reihe von Problemen gelöst werden können. Der Dateninhalt ist der berufliche Burnout der Lehrkräfte, der 28 Variablen enthält. Das Bild rechts zeigt die möglichen versteckten Variablen, die laut Experten zu diesen Burnout-Zuständen führen können (beobachtete Variablen), sowie die Beziehung zwischen den versteckten Variablen. Die durch die Analyse der beobachteten Daten mit der GIN-Methode erzielten Ergebnisse stimmen mit den Ergebnissen der Experten überein. Experten führen Analysen anhand qualitativen Hintergrundwissens durch, und die quantitative Analysemethode der Datenanalyse bietet Verifizierung und Unterstützung für Expertenergebnisse.
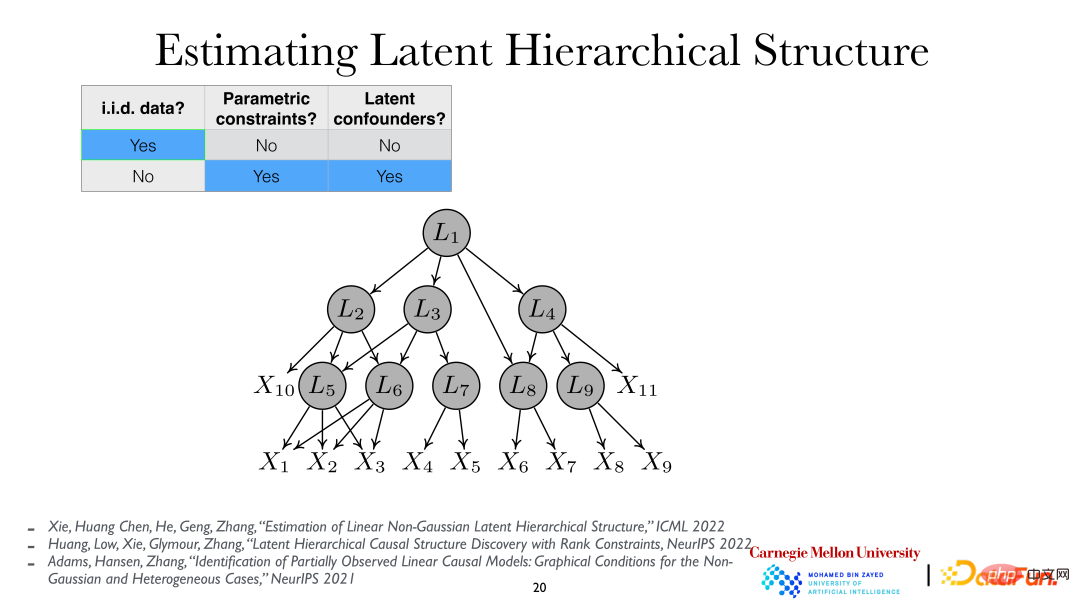
Für eine weitere eingehende Analyse kann davon ausgegangen werden, dass die latenten Variablen hierarchisch sind, dh die latente variable hierarchische Struktur (Latent Hierarchical Structure). Durch die Analyse der beobachteten Variablen xi können die verborgenen Variablen Li und ihre Beziehungen dahinter aufgedeckt werden.
3. Lernen der Kausaldarstellung aus Zeitreihen
Nachdem wir nun die Methode der Kausaldarstellung in der unabhängigen und identisch verteilten Situation verstanden haben, werden wir als nächstes vorstellen, wie man die verborgenen Variablen und die Kausalität dahinter unter nichtlinearen Bedingungen und unabhängig und identisch verteilt findet Situationen. Beziehung. Im Allgemeinen sind bei unabhängiger und identischer Verteilung relativ starke Bedingungen (einschließlich parametrischer Modellannahmen, linearer Modelle, dünn besetzter Graphen usw.) erforderlich, um den Kausalzusammenhang zu finden. In anderen Fällen kann die Ursache leichter gefunden werden.

Im Folgenden erfahren Sie, wie Sie kausale Darstellungen aus Zeitreihen finden, d Serie Dies ist ein klassisches Problem bei der Ermittlung der Kausalität aus Zeitreihendaten, also der Granger-Kausalität. Die Granger-Kausalität steht im Einklang mit der zuvor erwähnten Kausalität, die auf bedingter Unabhängigkeit basiert, jedoch mit der Hinzufügung von Zeitbeschränkungen (sofern sie nicht früher als die Ursache auftreten kann), und darüber hinaus können sofortige kausale Beziehungen eingeführt werden.

Das Bild oben zeigt eine praktischere Methode. Bei Videodaten besteht der wirklich bedeutungsvolle latente Prozess hinter den Daten darin, dass die von uns beobachteten Daten als Spiegelbild durch ihre Transformation durch eine reversible glatte nichtlineare Funktion erzeugt werden. Der eigentliche implizite kausale Prozess hat im Allgemeinen einen zeitlichen Kausalzusammenhang, wie zum Beispiel „schieben und dann fallen“. Dieser kausale Effekt ist im Allgemeinen zeitverzögert. Unter diesen Bedingungen kann der zugrunde liegende latente Prozess selbst unter sehr schwachen Annahmen vollständig verstanden werden (selbst wenn der zugrunde liegende latente Prozess nicht parametrisch ist und die g-Funktion (vom latenten Prozess zur beobachteten Zeitreihe) ebenfalls nicht parametrisch ist). Alles enthüllt.
Dies liegt daran, dass es nach der Rückkehr zum realen impliziten Prozess keine unmittelbare Kausalität und Abhängigkeit mehr gibt und die Beziehung zwischen Objekten klarer wird. Wenn Sie jedoch die falsche Analysemethode verwenden, um die Beobachtungsdaten zu betrachten, z. B. die Pixel der Videodaten direkt zu beobachten, werden Sie feststellen, dass zwischen ihnen eine sofortige Abhängigkeit besteht. 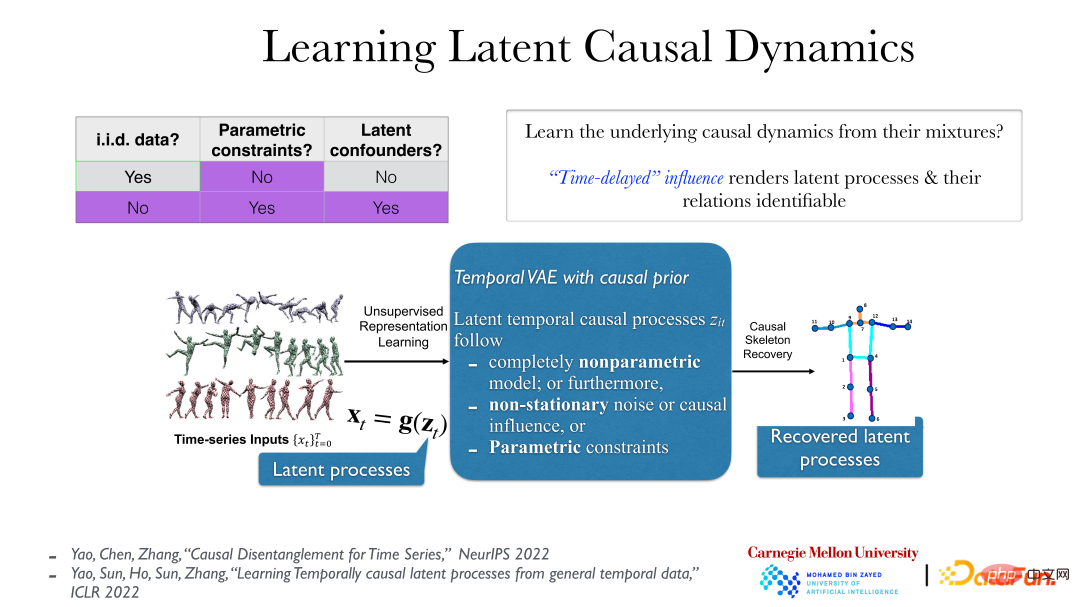
Das obige Bild zeigt zwei einfache Fälle: Die linke Seite zeigt die Videodaten von KiTTiMask. Wir erhalten drei versteckte Prozesse: Bewegen in eine Richtung und Ändern der Maskengröße. Die rechte Seite zeigt 5 kleine Kugeln unterschiedlicher Farbe. Durch die Analyse können 10 versteckte Variablen (x, y-Koordinaten der 5 kleinen Kugeln) und dann die Ursache und Wirkung zwischen ihnen ermittelt werden Beziehung gefunden werden (es gibt Federn zwischen einigen Kugeln). Basierend auf Videodaten können wir direkt eine völlig unbeaufsichtigte Methode verwenden und das Prinzip von Ursache und Wirkung einführen, um die Beziehung zwischen den dahinter stehenden Objekten zu ermitteln.
4. Lernen der kausalen Darstellung unter mehreren Verteilungen
Lassen Sie uns abschließend die kausale Analyse einführen, wenn sich die Datenverteilung ändert:

Bei der Aufzeichnung von Variablen/Prozessen im Laufe der Zeit wird häufig festgestellt, dass sich die Datenverteilung im Laufe der Zeit ändert. Dies ist auf eine Änderung des Werts der zugrunde liegenden unbeobachteten/gemessenen Variablen zurückzuführen, wodurch sich die Datenverteilung der beobachteten Variablen als Reaktion ändert. Wenn Sie Daten unter verschiedenen Bedingungen messen, werden Sie ebenfalls feststellen, dass die Verteilung der unter verschiedenen Bedingungen/Standorten gemessenen Daten ebenfalls unterschiedlich sein kann.
Hervorzuheben ist hier, dass ein sehr enger Zusammenhang zwischen Kausalmodellierung und Veränderungen in der Datenverteilung besteht. Wenn ein Kausalmodell angegeben wird, können sich diese Untermodule aufgrund der modularen Natur unabhängig voneinander ändern. Wenn diese Änderung anhand der Daten beobachtet werden kann, kann die Richtigkeit des Kausalmodells überprüft werden. Die hier erwähnte Änderung des Kausalmodells führt dazu, dass der kausale Einfluss stärker/schwächer werden oder sogar verschwinden kann.
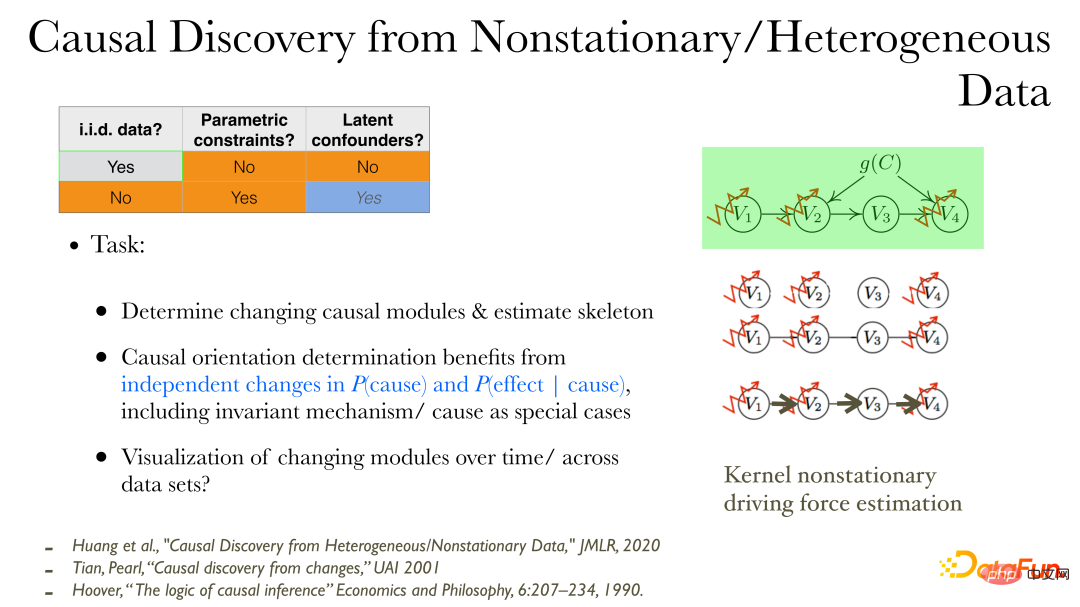
In instationären Daten/heterogenen Daten können kausale Zusammenhänge direkter entdeckt werden:
① Zunächst können Sie den kausalen Produktionsprozess beobachten, der sich ändert.
② Bestimmen Sie die ungerichtete Kante (Skelett) des kausalen Einflusses;
③ Finden Sie die Richtung der Ursache: Wenn sich die Datenverteilung ändert, können zusätzliche Eigenschaften verwendet werden: Änderungen in der Ursache und Änderungen in der Wirkung gemäß der Ursache sind unabhängig voneinander und haben keine Verbindung. Weil Änderungen zwischen verschiedenen Modulen unabhängig sind.
④ Verwenden Sie niedrigdimensionale Visualisierungsmethoden, um den Prozess kausaler Änderungen zu beschreiben.
Die folgende Abbildung zeigt einige Ergebnisse der Analyse der täglichen Aktienrenditedaten (Momentandaten, keine Zeitverzögerung) an der New Yorker Börse:
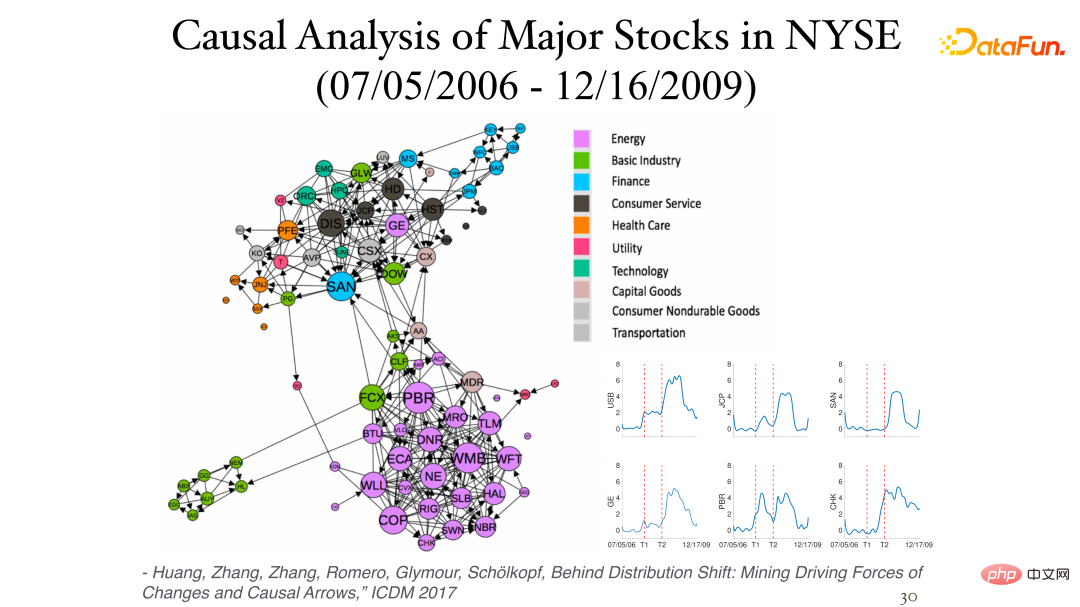
Die Asymmetrie zwischen ihnen kann durch den Einfluss der Nichtstationarität festgestellt werden. Verschiedene Sektoren gehören oft zur gleichen Kategorie (Cluster) und sind eng miteinander verbunden. Das Bild in der unteren rechten Ecke zeigt den kausalen Prozess der Bestandsveränderungen im Zeitverlauf, wobei die beiden vertikalen Achsen die Finanzkrisen von 2007 bzw. 2008 darstellen.
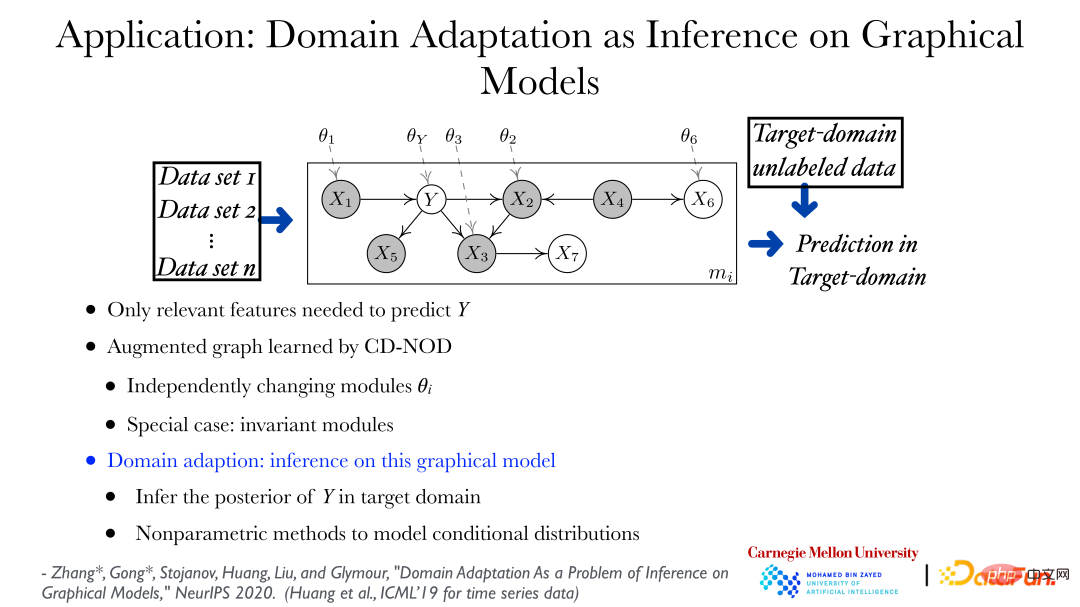
Durch die kausale Analysemethode unter Multiverteilungsbedingungen können die Änderungsmuster von Daten aus verschiedenen Datensätzen ermittelt werden, und die direkte Anwendung kann für Transferlernen und Domänenanpassung verwendet werden. Wie in der Abbildung oben gezeigt, können Sie die sich ändernden Regeln der Daten aus verschiedenen Datensätzen ermitteln und mithilfe eines erweiterten Diagramms zeigen, wie sich die Verteilung der Daten ändern kann. In der Abbildung stellt Theta_Y dar, dass Y ihm The gibt Die Verteilung unter dem übergeordneten Knoten kann sich je nach Domäne ändern. Basierend auf dem Diagramm, das die Änderungen in der Datenverteilung beschreibt, ist die Vorhersage von Y in einem neuen Feld oder Zielfeld ein sehr Standardproblem, das heißt, wie man die hintere Wahrscheinlichkeit von Y bei gegebenem Merkmalswert ermittelt, ist ein Inferenzproblem.
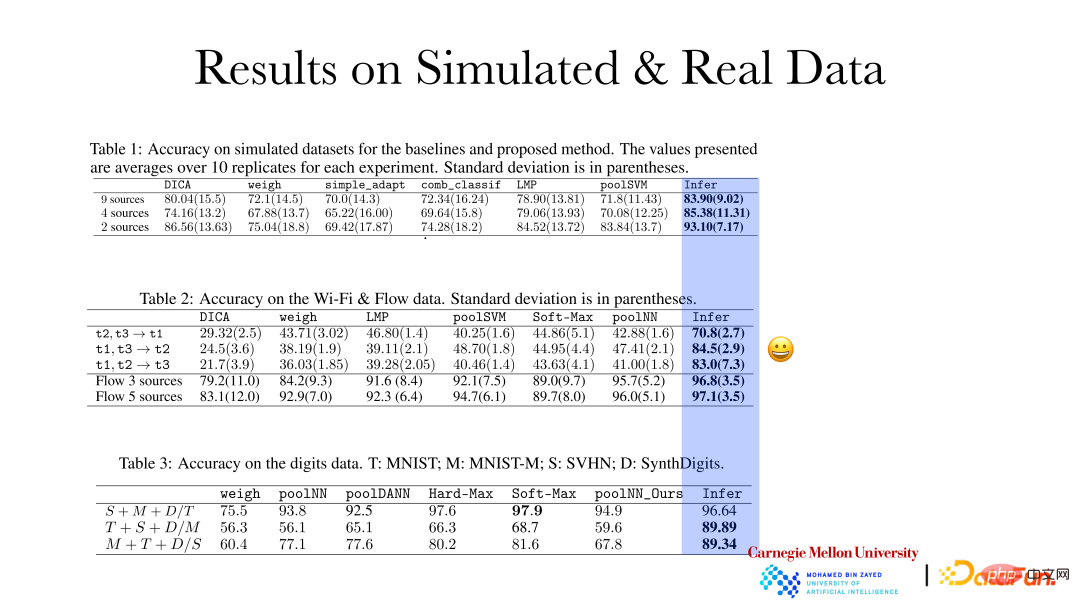
Die obige Abbildung zeigt, dass die Genauigkeit des Argumentationseffekts der Kausaldarstellungsmethode auf simulierte Daten und reale Daten erheblich verbessert wurde. Basierend auf den qualitativen Änderungsregeln und dem Ausmaß der Variabilität in verschiedenen Feldern werden adaptive Anpassungen vorgenommen, wenn neue Felder entstehen. Diese Art von Vorhersageeffekt wird besser sein.

Die obige Abbildung zeigt aktuelle Arbeiten im Zusammenhang mit Partial Disentanglement for Domain Adaption. Gehen Sie angesichts der Merkmale und Ziele davon aus, dass alles nicht parametrisch ist und sich einige Faktoren mit der Domäne nicht ändern. Das heißt, die Verteilung ist stabil, einige Faktoren können sich jedoch ändern. Ich hoffe, diese wenigen Faktoren zu finden, die die Verteilung ändern. Basierend auf den gefundenen Faktoren können verschiedene Bereiche miteinander in Einklang gebracht werden, und dann können die entsprechenden Beziehungen zwischen verschiedenen Bereichen gefunden werden, sodass Domänenanpassung/Transferlernen eine Selbstverständlichkeit ist. Es kann bewiesen werden, dass die unabhängigen Faktoren, die hinter den Änderungen in der Verteilung stehen, direkt aus den Beobachtungsdaten wiederhergestellt werden können und die unveränderten Faktoren ihren Unterraum wiederherstellen können. Wie in der Tabelle gezeigt, können mit den oben genannten Methoden gute Ergebnisse bei der Domänenanpassung erzielt werden. Gleichzeitig entspricht diese Methode auch dem Prinzip der minimalen Änderung, das heißt, man hofft, mithilfe des am wenigsten geänderten Faktors zu erklären, wie sich die Datenfaktoren in verschiedenen Feldern geändert haben, um ihnen zu entsprechen.

Zusammenfassend umfasst dieser Austausch hauptsächlich die folgenden Inhalte:
① Eine Reihe von Problemen des maschinellen Lernens erfordern eine geeignete Darstellung der dahinter stehenden Daten. Wenn Sie beispielsweise eine Entscheidung treffen, möchten Sie die Auswirkungen der Entscheidung kennen, damit Sie die optimale Entscheidung treffen können. Bei der Domänenanpassung/-generalisierung möchten Sie wissen, wie sich die Verteilung der Daten geändert hat Die optimale Vorhersage; beim verstärkenden Lernen ist die Interaktion des Agenten mit der Umgebung und die durch die Interaktion selbst hervorgerufene Belohnung ein kausales Problem, da der Benutzer vertrauenswürdige KI und erklärbare KI ist Fairness hängen alle mit der kausalen Repräsentation zusammen.
② Kausalität, einschließlich versteckter Variablen, kann unter bestimmten Bedingungen vollständig aus den Daten wiederhergestellt werden. Durch die Daten kann man die Natur des dahinter stehenden Prozesses wirklich verstehen und diese dann nutzen.
③ Kausalität ist kein Geheimnis. Solange es Daten gibt und die Hypothese angemessen ist, kann die Kausalität dahinter gefunden werden. Die hier getroffenen Annahmen sollten möglichst überprüfbar sein.
Generell hat das Kausalrepräsentationslernen große Anwendungsaussichten. Gleichzeitig gibt es viele Methoden, die dringend entwickelt werden müssen und gemeinsame Anstrengungen aller erfordern.
Das obige ist der detaillierte Inhalt vonCMU Zhang Kun: Neueste Fortschritte in der Kausaldarstellungstechnologie. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 Methoden und Schritte zur Verwendung von BERT für die Stimmungsanalyse in Python
Jan 22, 2024 pm 04:24 PM
Methoden und Schritte zur Verwendung von BERT für die Stimmungsanalyse in Python
Jan 22, 2024 pm 04:24 PM
BERT ist ein vorab trainiertes Deep-Learning-Sprachmodell, das 2018 von Google vorgeschlagen wurde. Der vollständige Name lautet BidirektionalEncoderRepresentationsfromTransformers, der auf der Transformer-Architektur basiert und die Eigenschaften einer bidirektionalen Codierung aufweist. Im Vergleich zu herkömmlichen Einweg-Codierungsmodellen kann BERT bei der Textverarbeitung gleichzeitig Kontextinformationen berücksichtigen, sodass es bei Verarbeitungsaufgaben in natürlicher Sprache eine gute Leistung erbringt. Seine Bidirektionalität ermöglicht es BERT, die semantischen Beziehungen in Sätzen besser zu verstehen und dadurch die Ausdrucksfähigkeit des Modells zu verbessern. Durch Vorschulungs- und Feinabstimmungsmethoden kann BERT für verschiedene Aufgaben der Verarbeitung natürlicher Sprache verwendet werden, wie z. B. Stimmungsanalyse und Benennung
 Analyse häufig verwendeter KI-Aktivierungsfunktionen: Deep-Learning-Praxis von Sigmoid, Tanh, ReLU und Softmax
Dec 28, 2023 pm 11:35 PM
Analyse häufig verwendeter KI-Aktivierungsfunktionen: Deep-Learning-Praxis von Sigmoid, Tanh, ReLU und Softmax
Dec 28, 2023 pm 11:35 PM
Aktivierungsfunktionen spielen beim Deep Learning eine entscheidende Rolle. Sie können nichtlineare Eigenschaften in neuronale Netze einführen und es dem Netz ermöglichen, komplexe Eingabe-Ausgabe-Beziehungen besser zu lernen und zu simulieren. Die richtige Auswahl und Verwendung von Aktivierungsfunktionen hat einen wichtigen Einfluss auf die Leistung und Trainingsergebnisse neuronaler Netze. In diesem Artikel werden vier häufig verwendete Aktivierungsfunktionen vorgestellt: Sigmoid, Tanh, ReLU und Softmax. Beginnend mit der Einführung, den Verwendungsszenarien und den Vorteilen. Nachteile und Optimierungslösungen werden besprochen, um Ihnen ein umfassendes Verständnis der Aktivierungsfunktionen zu vermitteln. 1. Sigmoid-Funktion Einführung in die Sigmoid-Funktionsformel: Die Sigmoid-Funktion ist eine häufig verwendete nichtlineare Funktion, die jede reelle Zahl auf Werte zwischen 0 und 1 abbilden kann. Es wird normalerweise verwendet, um das zu vereinheitlichen
 Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Heute diskutieren wir darüber, wie Deep-Learning-Technologie die Leistung von visionbasiertem SLAM (Simultaneous Localization and Mapping) in komplexen Umgebungen verbessern kann. Durch die Kombination von Methoden zur Tiefenmerkmalsextraktion und Tiefenanpassung stellen wir hier ein vielseitiges hybrides visuelles SLAM-System vor, das die Anpassung in anspruchsvollen Szenarien wie schlechten Lichtverhältnissen, dynamischer Beleuchtung, schwach strukturierten Bereichen und starkem Jitter verbessern soll. Unser System unterstützt mehrere Modi, einschließlich erweiterter Monokular-, Stereo-, Monokular-Trägheits- und Stereo-Trägheitskonfigurationen. Darüber hinaus wird analysiert, wie visuelles SLAM mit Deep-Learning-Methoden kombiniert werden kann, um andere Forschungen zu inspirieren. Durch umfangreiche Experimente mit öffentlichen Datensätzen und selbst abgetasteten Daten demonstrieren wir die Überlegenheit von SL-SLAM in Bezug auf Positionierungsgenauigkeit und Tracking-Robustheit.
 Latente Raumeinbettung: Erklärung und Demonstration
Jan 22, 2024 pm 05:30 PM
Latente Raumeinbettung: Erklärung und Demonstration
Jan 22, 2024 pm 05:30 PM
Latent Space Embedding (LatentSpaceEmbedding) ist der Prozess der Abbildung hochdimensionaler Daten auf niedrigdimensionalen Raum. Im Bereich des maschinellen Lernens und des tiefen Lernens handelt es sich bei der Einbettung latenter Räume normalerweise um ein neuronales Netzwerkmodell, das hochdimensionale Eingabedaten in einen Satz niedrigdimensionaler Vektordarstellungen abbildet. Dieser Satz von Vektoren wird oft als „latente Vektoren“ oder „latent“ bezeichnet Kodierungen". Der Zweck der Einbettung latenter Räume besteht darin, wichtige Merkmale in den Daten zu erfassen und sie in einer prägnanteren und verständlicheren Form darzustellen. Durch die Einbettung latenter Räume können wir Vorgänge wie das Visualisieren, Klassifizieren und Clustern von Daten im niedrigdimensionalen Raum durchführen, um die Daten besser zu verstehen und zu nutzen. Die Einbettung latenter Räume findet in vielen Bereichen breite Anwendung, z. B. bei der Bilderzeugung, der Merkmalsextraktion, der Dimensionsreduzierung usw. Die Einbettung des latenten Raums ist das Wichtigste
 Verstehen Sie in einem Artikel: die Zusammenhänge und Unterschiede zwischen KI, maschinellem Lernen und Deep Learning
Mar 02, 2024 am 11:19 AM
Verstehen Sie in einem Artikel: die Zusammenhänge und Unterschiede zwischen KI, maschinellem Lernen und Deep Learning
Mar 02, 2024 am 11:19 AM
In der heutigen Welle rasanter technologischer Veränderungen sind künstliche Intelligenz (KI), maschinelles Lernen (ML) und Deep Learning (DL) wie helle Sterne und führen die neue Welle der Informationstechnologie an. Diese drei Wörter tauchen häufig in verschiedenen hochaktuellen Diskussionen und praktischen Anwendungen auf, aber für viele Entdecker, die neu auf diesem Gebiet sind, sind ihre spezifische Bedeutung und ihre internen Zusammenhänge möglicherweise noch immer rätselhaft. Schauen wir uns also zunächst dieses Bild an. Es ist ersichtlich, dass zwischen Deep Learning, maschinellem Lernen und künstlicher Intelligenz ein enger Zusammenhang und eine fortschreitende Beziehung besteht. Deep Learning ist ein spezifischer Bereich des maschinellen Lernens und des maschinellen Lernens
 Super stark! Top 10 Deep-Learning-Algorithmen!
Mar 15, 2024 pm 03:46 PM
Super stark! Top 10 Deep-Learning-Algorithmen!
Mar 15, 2024 pm 03:46 PM
Fast 20 Jahre sind vergangen, seit das Konzept des Deep Learning im Jahr 2006 vorgeschlagen wurde. Deep Learning hat als Revolution auf dem Gebiet der künstlichen Intelligenz viele einflussreiche Algorithmen hervorgebracht. Was sind Ihrer Meinung nach die zehn besten Algorithmen für Deep Learning? Im Folgenden sind meiner Meinung nach die besten Algorithmen für Deep Learning aufgeführt. Sie alle nehmen hinsichtlich Innovation, Anwendungswert und Einfluss eine wichtige Position ein. 1. Hintergrund des Deep Neural Network (DNN): Deep Neural Network (DNN), auch Multi-Layer-Perceptron genannt, ist der am weitesten verbreitete Deep-Learning-Algorithmus. Als er erstmals erfunden wurde, wurde er aufgrund des Engpasses bei der Rechenleistung in Frage gestellt Jahre, Rechenleistung, Der Durchbruch kam mit der Datenexplosion. DNN ist ein neuronales Netzwerkmodell, das mehrere verborgene Schichten enthält. In diesem Modell übergibt jede Schicht Eingaben an die nächste Schicht und
 Sehen Sie sich von den Grundlagen bis zur Praxis die Entwicklungsgeschichte des Elasticsearch-Vektorabrufs an
Oct 23, 2023 pm 05:17 PM
Sehen Sie sich von den Grundlagen bis zur Praxis die Entwicklungsgeschichte des Elasticsearch-Vektorabrufs an
Oct 23, 2023 pm 05:17 PM
1. Einleitung Die Vektorabfrage ist zu einem Kernbestandteil moderner Such- und Empfehlungssysteme geworden. Es ermöglicht einen effizienten Abfrageabgleich und Empfehlungen, indem es komplexe Objekte (wie Text, Bilder oder Töne) in numerische Vektoren umwandelt und Ähnlichkeitssuchen in mehrdimensionalen Räumen durchführt. Schauen Sie sich von den Grundlagen bis zur Praxis die Entwicklungsgeschichte von Elasticsearch Vector Retrieval_elasticsearch an. Als beliebte Open-Source-Suchmaschine hat die Entwicklung von Elasticsearch im Bereich Vektor Retrieval schon immer große Aufmerksamkeit erregt. In diesem Artikel wird die Entwicklungsgeschichte des Elasticsearch-Vektorabrufs untersucht, wobei der Schwerpunkt auf den Merkmalen und dem Fortschritt jeder Phase liegt. Wenn Sie sich an der Geschichte orientieren, ist es für jeden praktisch, eine umfassende Palette zum Abrufen von Elasticsearch-Vektoren einzurichten.
 AlphaFold 3 wird auf den Markt gebracht und sagt die Wechselwirkungen und Strukturen von Proteinen und allen Lebensmolekülen umfassend und mit weitaus größerer Genauigkeit als je zuvor voraus
Jul 16, 2024 am 12:08 AM
AlphaFold 3 wird auf den Markt gebracht und sagt die Wechselwirkungen und Strukturen von Proteinen und allen Lebensmolekülen umfassend und mit weitaus größerer Genauigkeit als je zuvor voraus
Jul 16, 2024 am 12:08 AM
Herausgeber | Rettichhaut Seit der Veröffentlichung des leistungsstarken AlphaFold2 im Jahr 2021 verwenden Wissenschaftler Modelle zur Proteinstrukturvorhersage, um verschiedene Proteinstrukturen innerhalb von Zellen zu kartieren, Medikamente zu entdecken und eine „kosmische Karte“ jeder bekannten Proteininteraktion zu zeichnen. Gerade hat Google DeepMind das AlphaFold3-Modell veröffentlicht, das gemeinsame Strukturvorhersagen für Komplexe wie Proteine, Nukleinsäuren, kleine Moleküle, Ionen und modifizierte Reste durchführen kann. Die Genauigkeit von AlphaFold3 wurde im Vergleich zu vielen dedizierten Tools in der Vergangenheit (Protein-Ligand-Interaktion, Protein-Nukleinsäure-Interaktion, Antikörper-Antigen-Vorhersage) deutlich verbessert. Dies zeigt, dass dies innerhalb eines einzigen einheitlichen Deep-Learning-Frameworks möglich ist



