 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Um das Problem des VAE-Repräsentationslernens zu lösen, schlug die Universität Hokkaido ein neues generatives Modell GWAE vor
Um das Problem des VAE-Repräsentationslernens zu lösen, schlug die Universität Hokkaido ein neues generatives Modell GWAE vor
Um das Problem des VAE-Repräsentationslernens zu lösen, schlug die Universität Hokkaido ein neues generatives Modell GWAE vor
Das Erlernen niedrigdimensionaler Darstellungen hochdimensionaler Daten ist eine grundlegende Aufgabe beim unbeaufsichtigten Lernen, da solche Darstellungen das Wesentliche der Daten prägnant erfassen und es ermöglichen, nachgelagerte Aufgaben auf der Grundlage niedrigdimensionaler Eingaben auszuführen. Der Variational Autoencoder (VAE) ist eine wichtige Methode zum Repräsentationslernen, aufgrund seiner objektiven Steuerung ist das Repräsentationslernen jedoch immer noch eine anspruchsvolle Aufgabe. Obwohl das Evidence Lower Bound (ELBO)-Ziel von VAE generativ modelliert ist, ist das Lernen von Repräsentationen nicht direkt auf dieses Ziel ausgerichtet, was spezifische Modifikationen der Repräsentationslernaufgabe erfordert, wie z. B. Entflechtung. Diese Modifikationen führen manchmal zu impliziten und unerwünschten Änderungen im Modell, was das Lernen kontrollierter Darstellungen zu einer herausfordernden Aufgabe macht.
Um das Problem des Repräsentationslernens in Variations-Autoencodern zu lösen, schlägt dieser Artikel ein neues generatives Modell namens Gromov-Wasserstein Autoencoders (GWAE) vor. GWAE bietet ein neues Framework für das Repräsentationslernen basierend auf der Modellarchitektur des Variational Autoencoder (VAE). Im Gegensatz zu herkömmlichen VAE-basierten Darstellungslernmethoden zur generativen Modellierung von Datenvariablen erhält GWAE vorteilhafte Darstellungen durch optimale Übertragung zwischen Daten und latenten Variablen. Die Gromov-Wasserstein (GW)-Metrik ermöglicht einen solchen optimalen Transfer zwischen unvergleichbaren Variablen (z. B. Variablen mit unterschiedlichen Dimensionen), der sich auf die Distanzstruktur der betrachteten Variablen konzentriert. Durch Ersetzen des ELBO-Ziels durch die GW-Metrik führt GWAE einen Vergleich zwischen den Daten und dem latenten Raum durch und zielt direkt auf das Repräsentationslernen in Variations-Autoencodern ab (Abbildung 1). Diese Formulierung des Repräsentationslernens ermöglicht es den erlernten Darstellungen, spezifische Eigenschaften zu haben, die als vorteilhaft angesehen werden (z. B. Zerlegbarkeit), die als Meta-Priors bezeichnet werden.
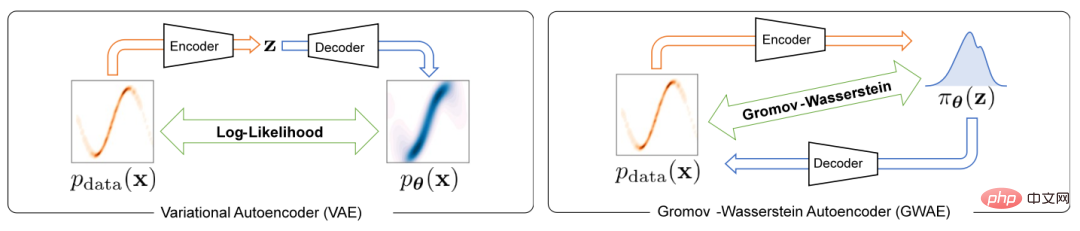
Abbildung 1 Der Unterschied zwischen VAE und GWAE
Diese Forschung wurde vom ICLR 2023 akzeptiert.
- Papier-Link: https://arxiv.org/abs/2209.07007
- Code-Link: https://github.com/ganmodokix/gwae
Methodeneinführung
Das GW-Ziel zwischen der Datenverteilung und der potenziellen vorherigen Verteilung ist wie folgt definiert:
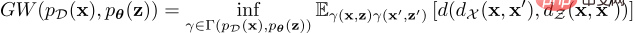
Diese Formel der optimalen Übertragungskosten kann die Inkonsistenz von Verteilungen in unvergleichlichen Räumen messen, jedoch aufgrund der Alle Kopplungen unterliegen einer unteren Grenze und es ist unpraktisch, genaue GW-Werte zu berechnen. Um dieses Problem zu lösen, löst GWAE ein entspanntes Optimierungsproblem, um den GW-Schätzer zu schätzen und zu minimieren, dessen Gradient durch automatische Differenzierung berechnet werden kann. Das Entspannungsziel ist die Summe der geschätzten GW-Metrik und drei Regularisierungsverluste, die alle in einem differenzierbaren Programmierframework wie PyTorch implementiert werden können. Dieses Entspannungsziel besteht aus einem Hauptverlust und drei Regularisierungsverlusten, nämlich dem geschätzten Haupt-GW-Verlust, dem WAE-basierten Rekonstruktionsverlust, dem Verlust der zusammengeführten ausreichenden Bedingung und dem Entropie-Regularisierungsverlust.
Dieses Schema kann auch die vorherige Verteilung flexibel anpassen, um vorteilhafte Funktionen in die niedrigdimensionale Darstellung einzuführen. In diesem Artikel werden insbesondere drei Prior-Populationen vorgestellt, nämlich:
Neural Prior (NP) In GWAEs mit NP wird ein vollständig verbundenes neuronales Netzwerk verwendet, um ein Prior-Sampling-Gerät zu konstruieren. Diese Familie früherer Verteilungen macht weniger Annahmen über die zugrunde liegenden Variablen und ist für allgemeine Situationen geeignet.
Faktorisierter neuronaler Prior (FNP) In GWAEs mit FNP wird ein Sampler mithilfe eines lokal verbundenen neuronalen Netzwerks erstellt, in dem Einträge für jede latente Variable unabhängig generiert werden. Dieser Sampler erzeugt eine faktorisierte Prior- und eine termisch unabhängige Darstellung, was eine wichtige Methode zur repräsentativen Meta-Prior-Entflechtung darstellt.
Gaussian Mixture Prior (GMP) In GMP ist es als eine Mischung aus mehreren Gaußschen Verteilungen definiert, und sein Sampler kann mithilfe starker Parametrisierungstechniken und Gumbel-Max-Techniken implementiert werden. GMP ermöglicht die Hypothese von Clustern in der Darstellung, wobei erwartet wird, dass jede Gaußsche Komponente des Priors einen Cluster erfasst.
Experimente und Ergebnisse
Diese Studie bewertet GWAE empirisch mit zwei Hauptmetaprioren: Entflechtung und Clusterbildung.
Entflechtung Die Studie nutzte den 3D-Shapes-Datensatz und die DCI-Metrik, um die Entwirrungsfähigkeit von GWAE zu messen. Die Ergebnisse zeigen, dass GWAE mithilfe von FNP in der Lage ist, Objektfarbtonfaktoren auf einer einzelnen Achse zu lernen, was die Entwirrungsfähigkeit von GWAE demonstriert. Auch die quantitative Auswertung belegt die Entflechtungsleistung von GWAE.
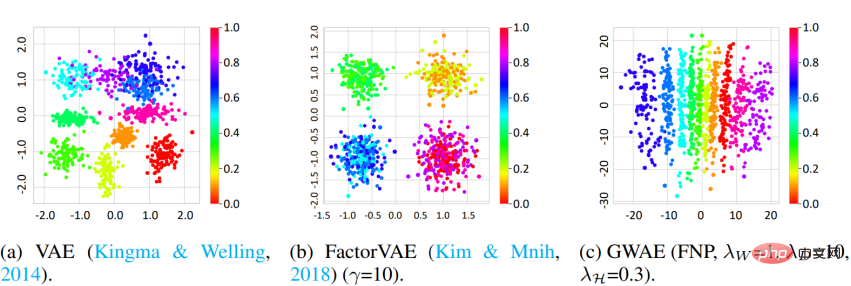
Clustering Um die auf der Metaprioris-Clusterung basierenden Darstellungen zu bewerten, führte diese Studie eine Out-of-Distribution (OoD)-Erkennung durch. Der MNIST-Datensatz wird als In-Distribution-Daten (ID) und der Omniglot-Datensatz als OoD-Daten verwendet. Während MNIST handgeschriebene Zahlen enthält, enthält Omniglot handgeschriebene Buchstaben mit unterschiedlichen Buchstaben. In diesem Experiment teilen sich die ID- und OoD-Datensätze die Domäne handschriftlicher Bilder, enthalten jedoch unterschiedliche Zeichen. Modelle werden auf ID-Daten trainiert und verwenden dann ihre erlernten Darstellungen, um ID- oder OoD-Daten zu erkennen. Bei VAE und DAGMM ist die für die OoD-Erkennung verwendete Variable die Prior-Log-Likelihood, während es bei GWAE das Kantorovich-Potenzial ist. Der Prior für GWAE wurde mit GMP erstellt, um die Cluster von MNIST zu erfassen. Die ROC-Kurve zeigt die OoD-Erkennungsleistung der Modelle, wobei alle drei Modelle eine nahezu perfekte Leistung erzielen, das mit GMP erstellte GWAE schnitt jedoch in Bezug auf die Fläche unter der Kurve (AUC) am besten ab.
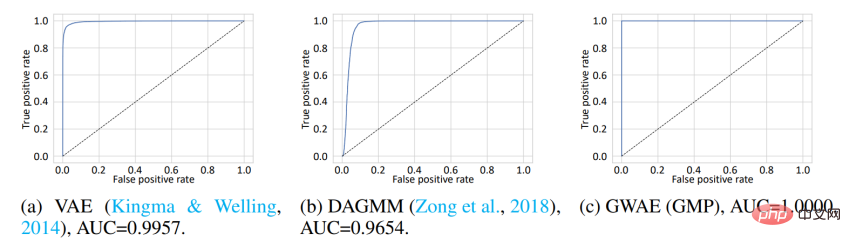
Darüber hinaus wurde in dieser Studie die generative Fähigkeit von GWAE bewertet.
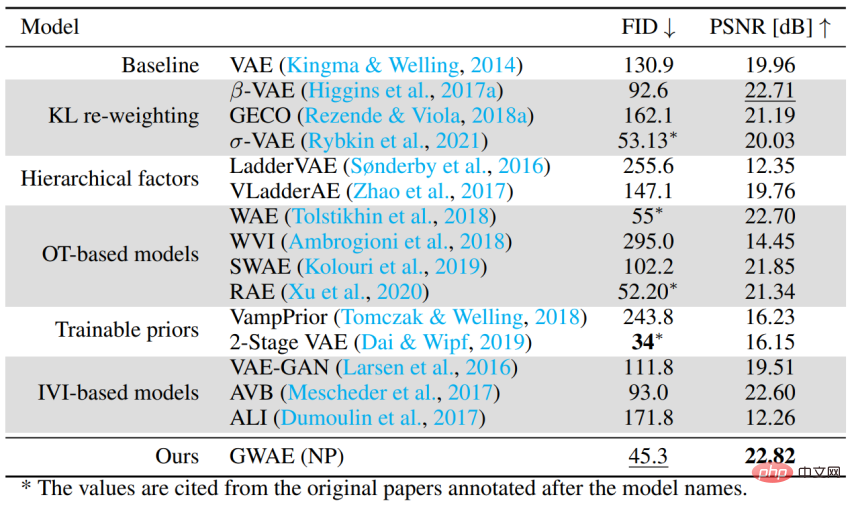
Leistung als Autoencoder-basiertes generatives Modell Um die Fähigkeit von GWAE zu bewerten, den allgemeinen Fall ohne spezifische Metaprioren zu verarbeiten, wurde die generative Leistung mithilfe des CelebA-Datensatzes bewertet. Das Experiment verwendet FID, um die generative Leistung des Modells zu bewerten, und PSNR, um die Leistung der automatischen Kodierung zu bewerten. GWAE erreichte mit NP die zweitbeste generative Leistung und die beste Autoenkodierungsleistung und demonstrierte damit seine Fähigkeit, die Datenverteilung in seinem Modell und die Dateninformationen in seiner Darstellung zu erfassen.
Zusammenfassung
- GWAE ist ein generatives Variations-Autoencoder-Modell, das auf der Gromov-Wasserstein-Metrik basiert und für die direkte Durchführung des Repräsentationslernens konzipiert ist.
- Da der Prior nur differenzierbare Stichproben erfordert, können verschiedene Prior-Verteilungseinstellungen erstellt werden, um Meta-Priors (ideale Eigenschaften der Darstellung) anzunehmen.
- Experimente zu primären Metaprioren und zur Leistungsbewertung als Variations-Autoencoder zeigen die Flexibilität der GWAE-Formulierung und die Repräsentationslernfähigkeiten von GWAE.
- Persönliche Homepage des Erstautors Nao Nakagawa: https://ganmodokix.com/note/cv
- Homepage des Hokkaido University Multimedia Laboratory: https://www-lmd.ist.hokudai /
Das obige ist der detaillierte Inhalt vonUm das Problem des VAE-Repräsentationslernens zu lösen, schlug die Universität Hokkaido ein neues generatives Modell GWAE vor. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 KI-Startups wechselten gemeinsam ihre Jobs zu OpenAI, und das Sicherheitsteam formierte sich neu, nachdem Ilya gegangen war!
Jun 08, 2024 pm 01:00 PM
KI-Startups wechselten gemeinsam ihre Jobs zu OpenAI, und das Sicherheitsteam formierte sich neu, nachdem Ilya gegangen war!
Jun 08, 2024 pm 01:00 PM
Letzte Woche wurde OpenAI inmitten der Welle interner Kündigungen und externer Kritik von internen und externen Problemen geplagt: - Der Verstoß gegen die Schwester der Witwe löste weltweit hitzige Diskussionen aus - Mitarbeiter, die „Overlord-Klauseln“ unterzeichneten, wurden einer nach dem anderen entlarvt – Internetnutzer listeten Ultramans „ Sieben Todsünden“ – Gerüchtebekämpfung: Laut durchgesickerten Informationen und Dokumenten, die Vox erhalten hat, war sich die leitende Führung von OpenAI, darunter Altman, dieser Eigenkapitalrückgewinnungsbestimmungen wohl bewusst und hat ihnen zugestimmt. Darüber hinaus steht OpenAI vor einem ernsten und dringenden Problem – der KI-Sicherheit. Die jüngsten Abgänge von fünf sicherheitsrelevanten Mitarbeitern, darunter zwei der prominentesten Mitarbeiter, und die Auflösung des „Super Alignment“-Teams haben die Sicherheitsprobleme von OpenAI erneut ins Rampenlicht gerückt. Das Fortune-Magazin berichtete, dass OpenA
 So bewerten Sie die Kosteneffizienz der kommerziellen Unterstützung für Java-Frameworks
Jun 05, 2024 pm 05:25 PM
So bewerten Sie die Kosteneffizienz der kommerziellen Unterstützung für Java-Frameworks
Jun 05, 2024 pm 05:25 PM
Die Bewertung des Kosten-/Leistungsverhältnisses des kommerziellen Supports für ein Java-Framework umfasst die folgenden Schritte: Bestimmen Sie das erforderliche Maß an Sicherheit und Service-Level-Agreement-Garantien (SLA). Die Erfahrung und das Fachwissen des Forschungsunterstützungsteams. Erwägen Sie zusätzliche Services wie Upgrades, Fehlerbehebung und Leistungsoptimierung. Wägen Sie die Kosten für die Geschäftsunterstützung gegen Risikominderung und Effizienzsteigerung ab.
 Das 70B-Modell generiert 1.000 Token in Sekunden, das Umschreiben des Codes übertrifft GPT-4o, vom Cursor-Team, einem von OpenAI investierten Code-Artefakt
Jun 13, 2024 pm 03:47 PM
Das 70B-Modell generiert 1.000 Token in Sekunden, das Umschreiben des Codes übertrifft GPT-4o, vom Cursor-Team, einem von OpenAI investierten Code-Artefakt
Jun 13, 2024 pm 03:47 PM
Beim Modell 70B können 1000 Token in Sekunden generiert werden, was fast 4000 Zeichen entspricht! Die Forscher haben Llama3 verfeinert und einen Beschleunigungsalgorithmus eingeführt. Im Vergleich zur nativen Version ist die Geschwindigkeit 13-mal höher! Es ist nicht nur schnell, seine Leistung bei Code-Rewriting-Aufgaben übertrifft sogar GPT-4o. Diese Errungenschaft stammt von anysphere, dem Team hinter dem beliebten KI-Programmierartefakt Cursor, und auch OpenAI beteiligte sich an der Investition. Sie müssen wissen, dass bei Groq, einem bekannten Framework zur schnellen Inferenzbeschleunigung, die Inferenzgeschwindigkeit von 70BLlama3 nur mehr als 300 Token pro Sekunde beträgt. Aufgrund der Geschwindigkeit von Cursor kann man sagen, dass eine nahezu sofortige vollständige Bearbeitung der Codedatei möglich ist. Manche Leute nennen es einen guten Kerl, wenn man Curs sagt
 Wie ist die Lernkurve von PHP-Frameworks im Vergleich zu anderen Sprach-Frameworks?
Jun 06, 2024 pm 12:41 PM
Wie ist die Lernkurve von PHP-Frameworks im Vergleich zu anderen Sprach-Frameworks?
Jun 06, 2024 pm 12:41 PM
Die Lernkurve eines PHP-Frameworks hängt von Sprachkenntnissen, Framework-Komplexität, Dokumentationsqualität und Community-Unterstützung ab. Die Lernkurve von PHP-Frameworks ist im Vergleich zu Python-Frameworks höher und im Vergleich zu Ruby-Frameworks niedriger. Im Vergleich zu Java-Frameworks haben PHP-Frameworks eine moderate Lernkurve, aber eine kürzere Einstiegszeit.
 Wie wirken sich die Lightweight-Optionen von PHP-Frameworks auf die Anwendungsleistung aus?
Jun 06, 2024 am 10:53 AM
Wie wirken sich die Lightweight-Optionen von PHP-Frameworks auf die Anwendungsleistung aus?
Jun 06, 2024 am 10:53 AM
Das leichte PHP-Framework verbessert die Anwendungsleistung durch geringe Größe und geringen Ressourcenverbrauch. Zu seinen Merkmalen gehören: geringe Größe, schneller Start, geringer Speicherverbrauch, verbesserte Reaktionsgeschwindigkeit und Durchsatz sowie reduzierter Ressourcenverbrauch. Praktischer Fall: SlimFramework erstellt eine REST-API, nur 500 KB, hohe Reaktionsfähigkeit und hoher Durchsatz
 China Mobile: Die Menschheit tritt in die vierte industrielle Revolution ein und kündigte offiziell „drei Pläne' an
Jun 27, 2024 am 10:29 AM
China Mobile: Die Menschheit tritt in die vierte industrielle Revolution ein und kündigte offiziell „drei Pläne' an
Jun 27, 2024 am 10:29 AM
Laut Nachrichten vom 26. Juni hielt Yang Jie, Vorsitzender von China Mobile, bei der Eröffnungszeremonie der World Mobile Communications Conference Shanghai (MWC Shanghai) 2024 eine Rede. Er sagte, dass die menschliche Gesellschaft derzeit in die vierte industrielle Revolution eintritt, die von Informationen dominiert und tief in Informationen und Energie integriert ist, d. h. die „Revolution der digitalen Intelligenz“, und dass sich die Bildung neuer Produktivkräfte beschleunigt. Yang Jie glaubt, dass jede Runde der industriellen Revolution darauf basiert, von der „Mechanisierungsrevolution“, angetrieben durch Dampfmaschinen, über die „Elektrifizierungsrevolution“, angetrieben durch Elektrizität und Verbrennungsmotoren, bis hin zur „Informationsrevolution“, angetrieben durch Computer und das Internet „Information und „Energie“ ist die Hauptlinie, die Produktivitätsentwicklung bringt
 So wählen Sie das beste Golang-Framework für verschiedene Anwendungsszenarien aus
Jun 05, 2024 pm 04:05 PM
So wählen Sie das beste Golang-Framework für verschiedene Anwendungsszenarien aus
Jun 05, 2024 pm 04:05 PM
Wählen Sie das beste Go-Framework basierend auf Anwendungsszenarien aus: Berücksichtigen Sie Anwendungstyp, Sprachfunktionen, Leistungsanforderungen und Ökosystem. Gängige Go-Frameworks: Gin (Webanwendung), Echo (Webdienst), Fiber (hoher Durchsatz), gorm (ORM), fasthttp (Geschwindigkeit). Praktischer Fall: Erstellen einer REST-API (Fiber) und Interaktion mit der Datenbank (gorm). Wählen Sie ein Framework: Wählen Sie fasthttp für die Schlüsselleistung, Gin/Echo für flexible Webanwendungen und gorm für die Datenbankinteraktion.
 Die Insidergeschichte des Suchalgorithmus von Google wurde enthüllt und 2.500 Seiten mit Dokumenten mit echten Namen wurden durchgesickert! Such-Ranking-Lügen aufgedeckt
Jun 11, 2024 am 09:14 AM
Die Insidergeschichte des Suchalgorithmus von Google wurde enthüllt und 2.500 Seiten mit Dokumenten mit echten Namen wurden durchgesickert! Such-Ranking-Lügen aufgedeckt
Jun 11, 2024 am 09:14 AM
Kürzlich wurden 2.500 Seiten interner Google-Dokumente durchgesickert und enthüllten, wie die Suche, „der mächtigste Schiedsrichter im Internet“, funktioniert. Der Mitbegründer und CEO von SparkToro ist eine anonyme Person. Er veröffentlichte einen Blog-Beitrag auf seiner persönlichen Website, in dem er behauptete, dass „eine anonyme Person mit mir Tausende von Seiten durchgesickerter Google Search API-Dokumentation geteilt hat, die jeder im SEO lesen sollte.“ ! „RandFishkin ist seit vielen Jahren der führende Sprecher im Bereich SEO (Suchmaschinenoptimierung), und er hat das Konzept der „Website-Autorität“ (DomainRating) vorgeschlagen. Da er auf diesem Gebiet hohes Ansehen genießt, RandFishkin





