Technologie-Peripheriegeräte
KI
Unverzichtbare Datenwissenschaft: 10 wichtige Konzepte + die Bedeutung von 22 Diagrammen
Unverzichtbare Datenwissenschaft: 10 wichtige Konzepte + die Bedeutung von 22 Diagrammen
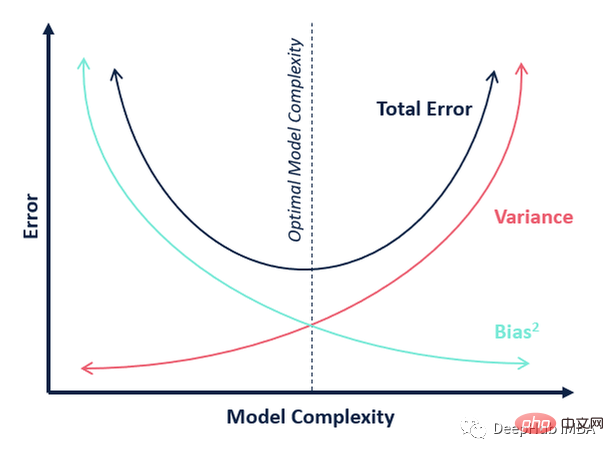
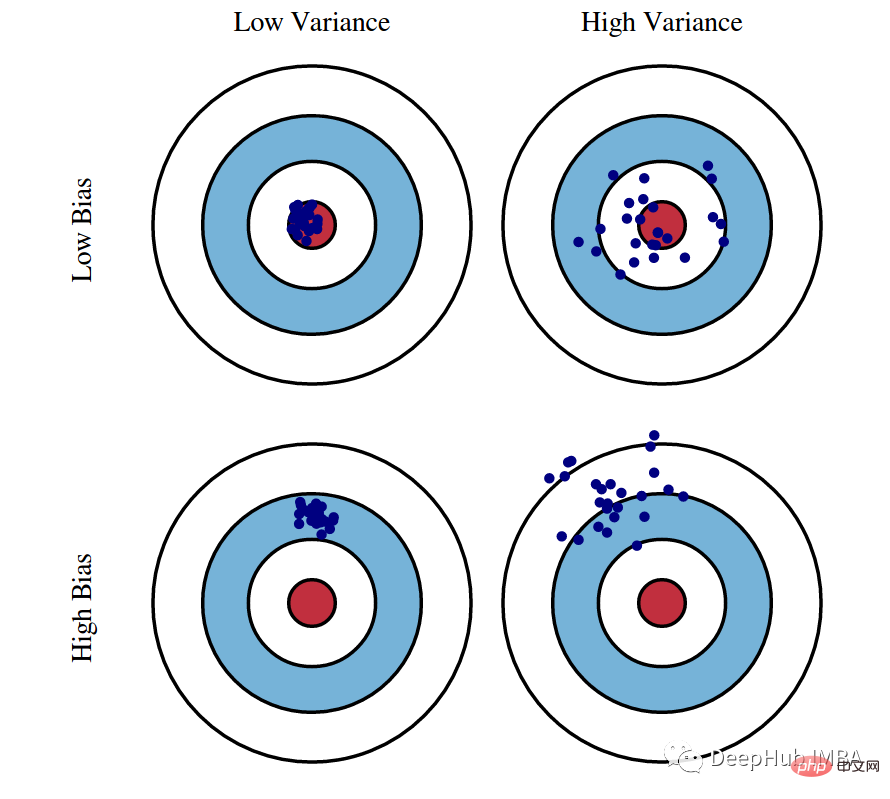
01 Bias-Varianz-Kompromiss
Dies ist ein Konzept, das immer einen hohen Stellenwert unter den wichtigsten Theorien des maschinellen Lernens einnimmt. Fast alle Algorithmen im maschinellen Lernen (einschließlich Deep Learning) streben danach, das richtige Gleichgewicht zwischen Bias und Varianz zu finden, und dieses Diagramm erklärt deutlich den Gegensatz zwischen beiden.
02 Gini-Unreinheit und Entropie
Gini (ein Maß für mangelnde Homogenität) und Entropie (ein Maß für Zufälligkeit) sind beide Maße für Knotenunreinheit in Entscheidungsbäumen.
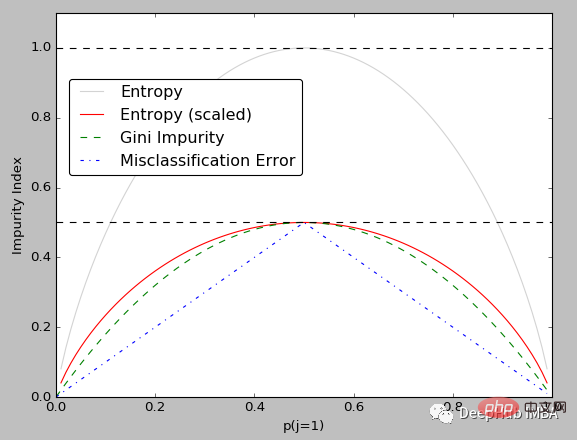
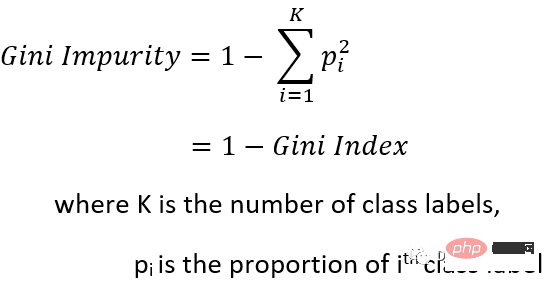
Für diese beiden Konzepte ist es wichtiger, die Beziehung zwischen ihnen zu verstehen, um in einem bestimmten Szenario den richtigen Indikator auswählen zu können.
Gini-Verunreinigung (Koeffizient) ist normalerweise einfacher zu berechnen als Entropie (da Entropie logarithmische Berechnungen beinhaltet).
03 Präzision vs. Recall-Kurve
Die Präzisions-Recall-Kurve zeigt den Kompromiss zwischen Präzision und Recall für verschiedene Schwellenwerte. Ein großer Bereich unter der Kurve stellt einen hohen Rückruf und eine hohe Präzision dar, wobei eine hohe Präzision mit niedrigen Fehlalarmraten und ein hoher Rückruf mit niedrigen Fehlalarmraten zusammenhängt.
Es hilft uns, den richtigen Schwellenwert entsprechend unseren Bedürfnissen zu wählen. Wenn es beispielsweise unser Ziel ist, Fehler vom Typ 1 zu reduzieren, müssen wir eine hohe Präzision wählen, während wir, wenn unser Ziel darin besteht, Fehler vom Typ 2 zu minimieren, einen Schwellenwert wählen sollten, der den Rückruf hoch macht.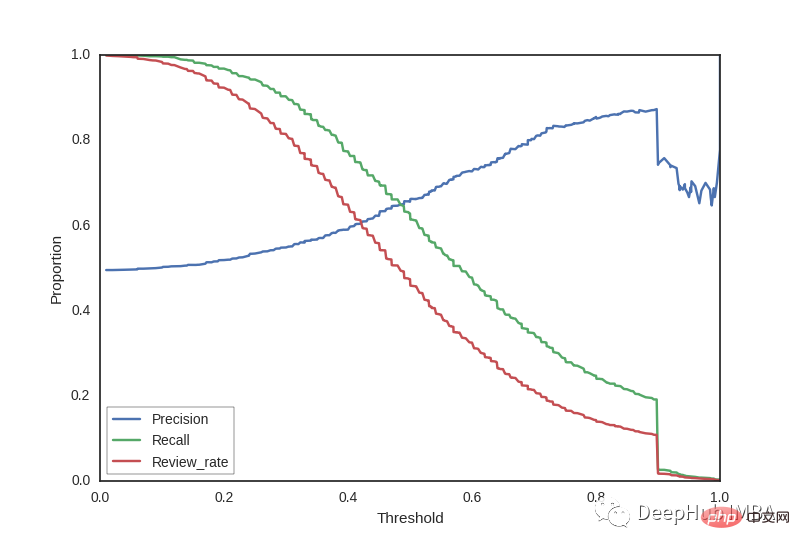 
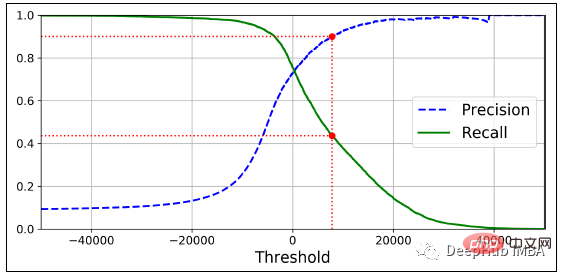
- Der Genauigkeitsnenner ist eine Variable: d. h. falsch positive Ergebnisse (als positiv eingestufte negative Proben) ändern sich jedes Mal.
- Der Recall-Nenner ist eine Konstante: Er stellt die Gesamtzahl der wahren Werte dar und bleibt daher immer gleich.
Deshalb hat Precision im Bild unten eine Welle am Ende, während Recall immer flach bleibt.
04 ROC-Kurve
Eine ROC-Kurve ist ein Diagramm, das die Leistung eines Klassifizierungsmodells bei allen Klassifizierungsschwellenwerten zeigt.
Diese Kurve stellt zwei Parameter dar:
真阳性率<br>误报率
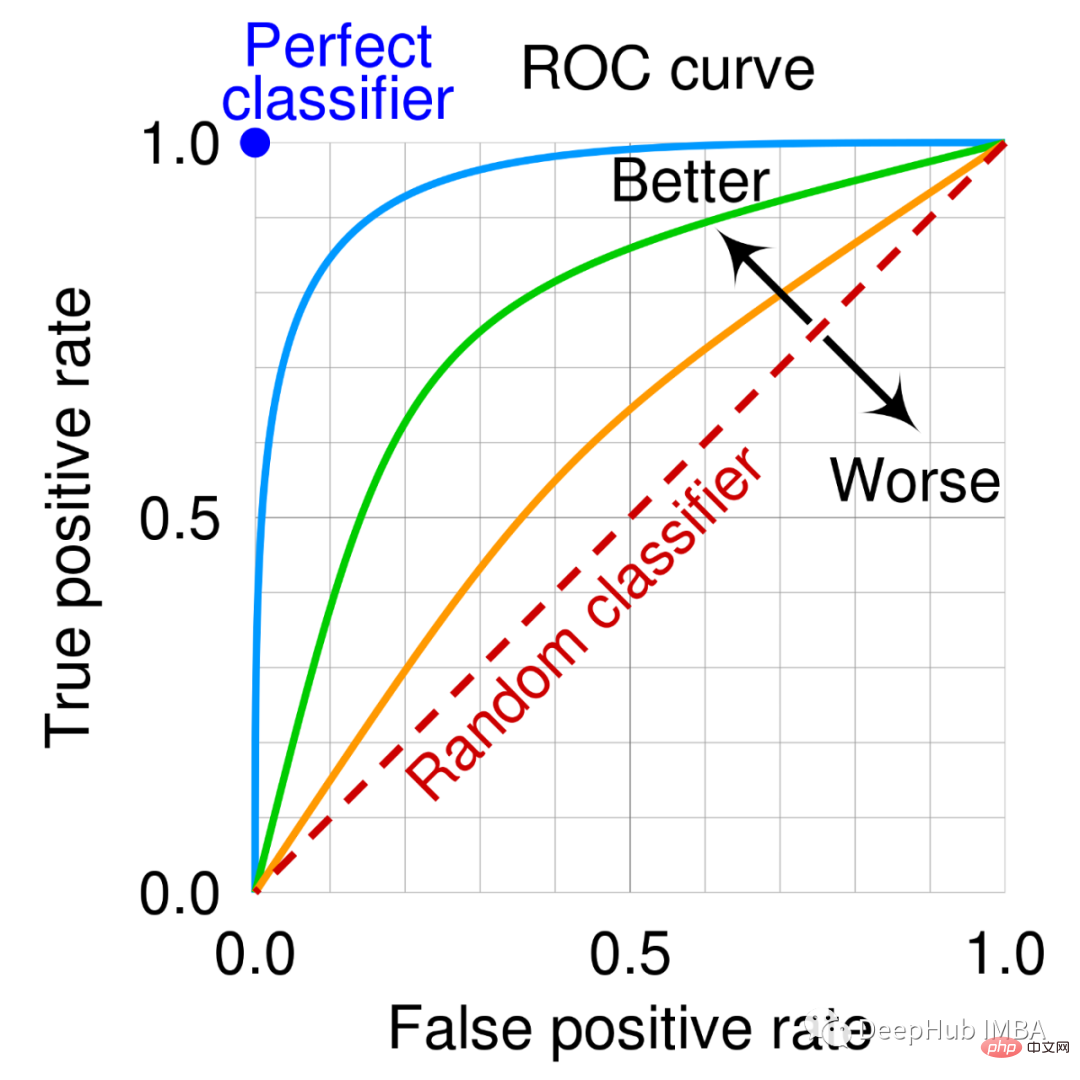
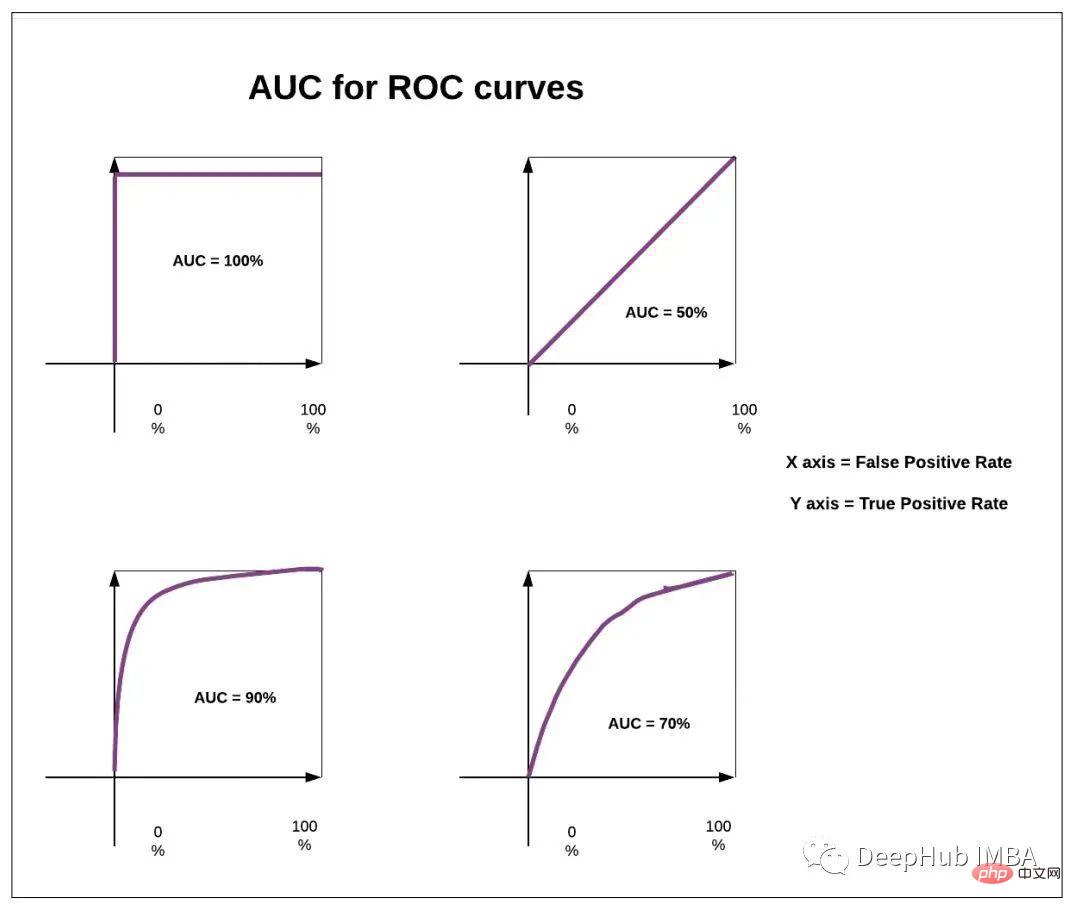
Die Fläche unter dieser Kurve (AUC genannt) kann auch als Leistungsmetrik verwendet werden. Je höher die AUC, desto besser das Modell.
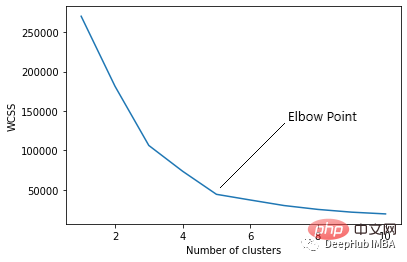
05 弯头曲线
用于K-means算法中最优簇数的选择。WCSS（簇内平方和）是给定簇中每个点与质心之间的平方距离之和。当我们用 K（簇数）值绘制 WCSS 时，该图看起来像一个肘部（弯头）。
随着聚类数量的增加，WCSS 值将开始下降。K = 1时WCSS值最大
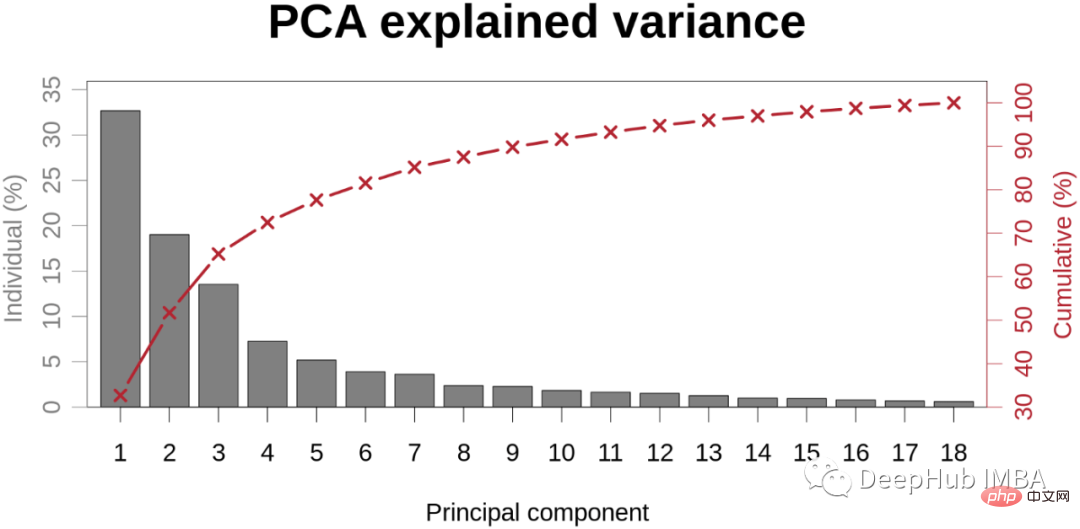
06三块地块
它帮助我们在对高维数据执行主成分分析后，可视化每个主成分解释的变异百分比。为了选择正确数量的主成分来考虑我们的模型，我们通常会绘制此图并选择能够为我们提供足够好的总体方差百分比的值。
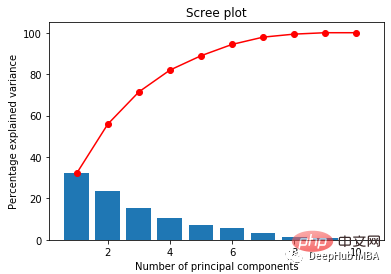
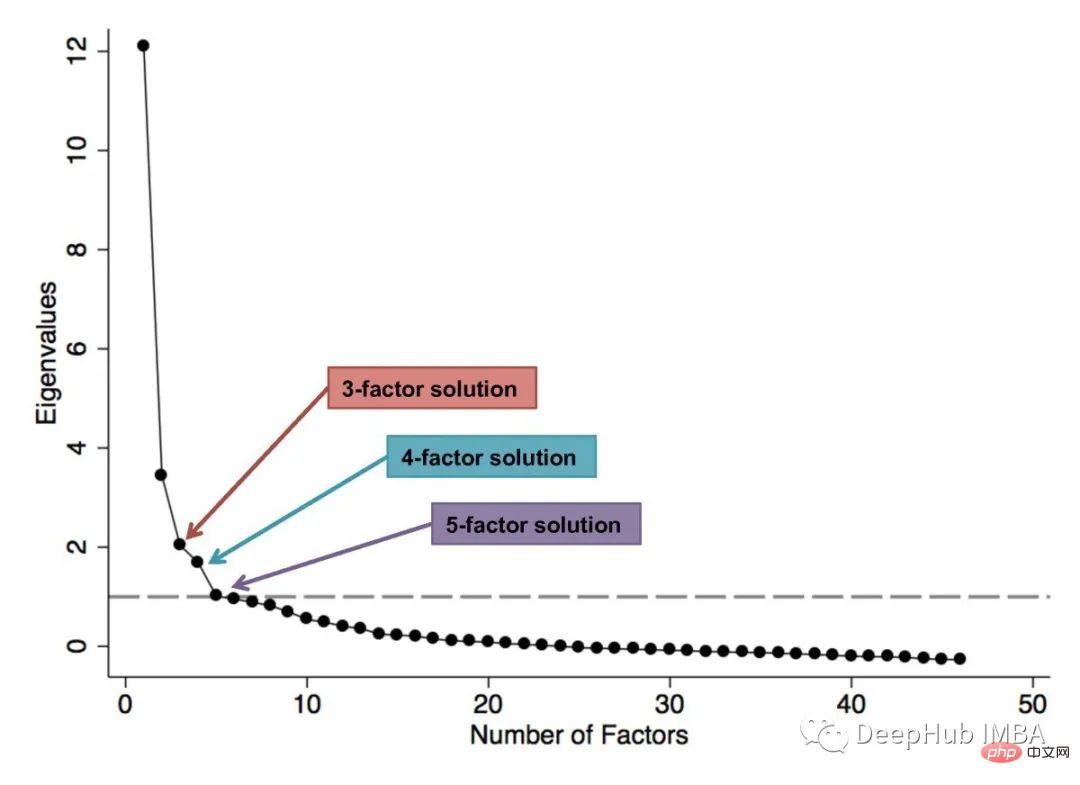
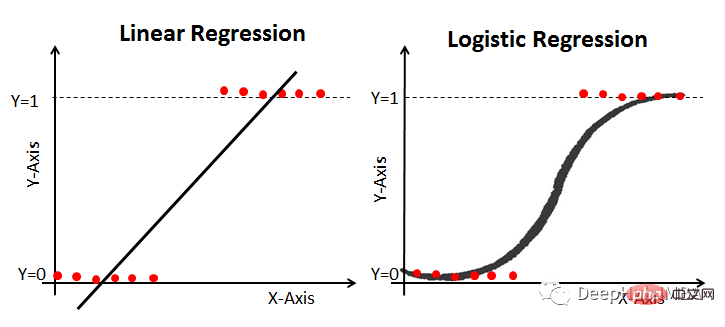
07线性和逻辑回归曲线
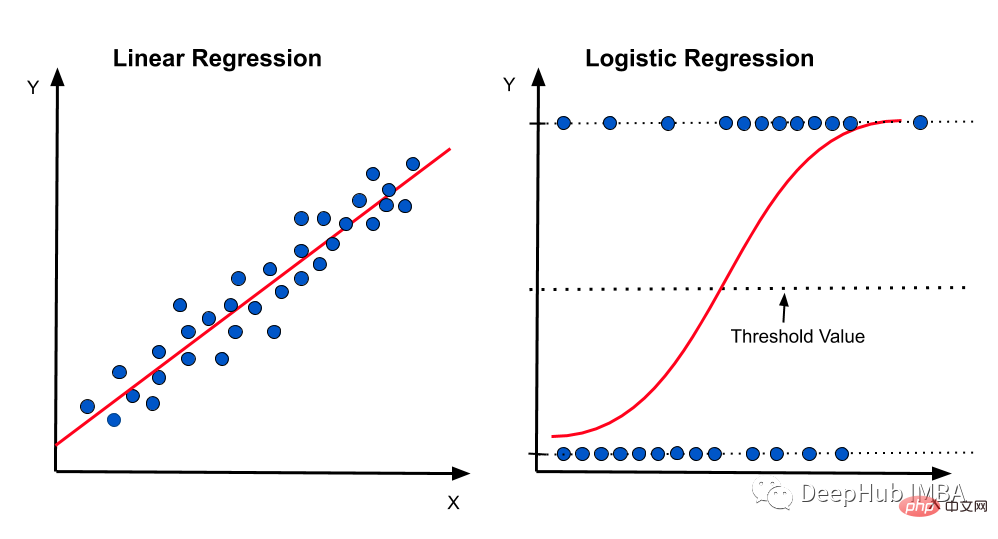
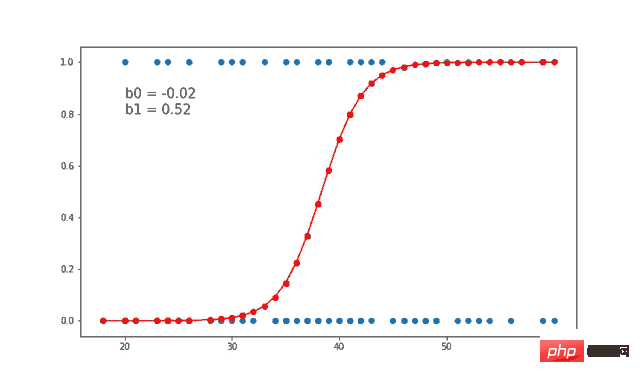
对于线性可分数据，我们可以进行线性回归或逻辑回归，二者都可以作为决策边界曲线/线。但是，在逻辑回归的情况下，由于通常只有 2 个类别，因此具有线性直线决策边界可能不起作用，在一条直线上值从低到高非常均匀地上升，因为它不够陡峭在值突然上升后会得到很多临界的高值或者低值，最终会错误分类。因此，"边界"区域，即概率从高到低转变的区域并不真正存在。所以一般情况下会应用 sigmoid 变换将其转换为 sigmoid 曲线，该曲线在极端情况下是平滑的，在中间几乎是线性的。
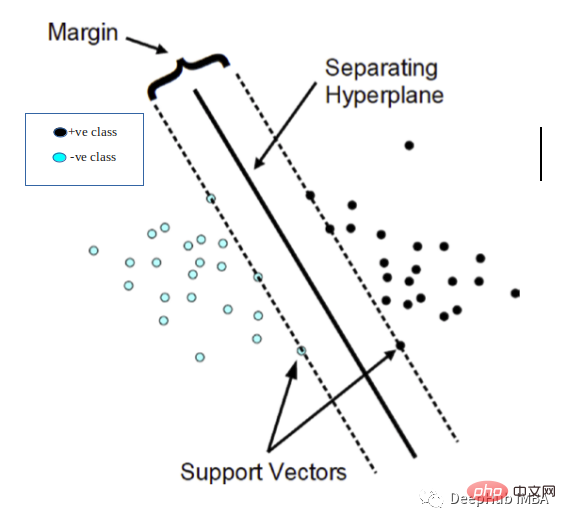
08支持向量机（几何理解）
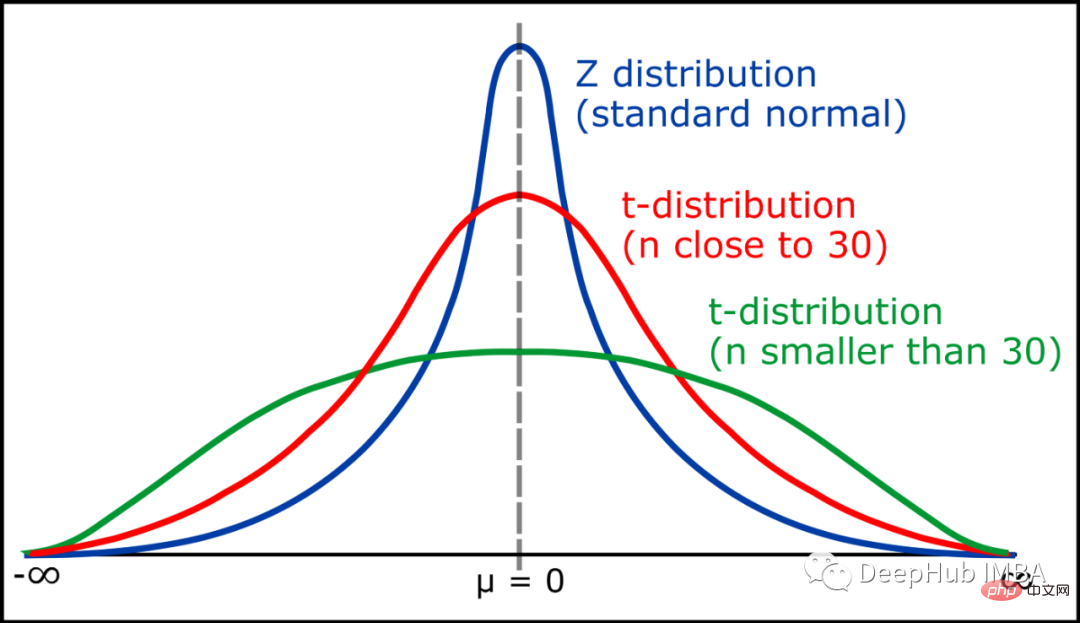
09标准正态分布规则（z-分布）
均值为0，标准差为1的特殊正态分布。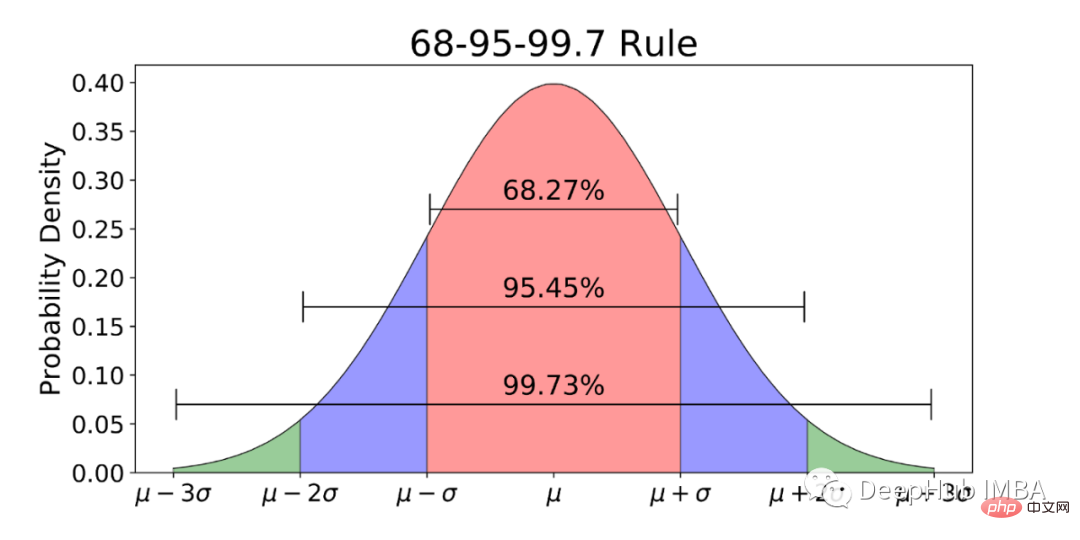
经验法则指出，按照正态分布观察到的数据中有 99.7% 位于平均值的 3 个标准差以内。根据该规则，68% 的数据在一个标准差内，95% 在两个标准差内，99.7% 在三个标准差内。10学生T分布T 分布（也称为学生 T 分布）是一系列分布，看起来几乎与正态分布曲线相同，只是更短和更宽/更胖。当我们有较小的样本时，我们使用 T分布而不是正态分布。样本量越大，t 分布越像正态分布。事实上，在 30 个样本之后，T 分布几乎与正态分布完全一样。
Zusammenfassung
Möglicherweise stoßen wir auf viele kleine, aber entscheidende Konzepte, die die Grundlage dafür bilden, dass wir eine Entscheidung treffen oder das richtige Modell auswählen. Die in diesem Artikel erwähnten wichtigen Konzepte können durch entsprechende Diagramme dargestellt werden, und wir müssen ihre Bedeutung kennen, wenn wir sie zum ersten Mal sehen. Wenn Sie die oben genannten Konzepte beherrschen, können Sie versuchen, sie im Folgenden zu erklären Bild stellt dar:
Das obige ist der detaillierte Inhalt vonUnverzichtbare Datenwissenschaft: 10 wichtige Konzepte + die Bedeutung von 22 Diagrammen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
Heiße KI -Werkzeuge
Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos
AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.
Undress AI Tool
Ausziehbilder kostenlos
Clothoff.io
KI-Kleiderentferner
AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.
Heißer Artikel
Heiße Werkzeuge
Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor
SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen
Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung
Dreamweaver CS6
Visuelle Webentwicklungstools
SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)
Heiße Themen
1376
52
In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In den Bereichen maschinelles Lernen und Datenwissenschaft stand die Interpretierbarkeit von Modellen schon immer im Fokus von Forschern und Praktikern. Mit der weit verbreiteten Anwendung komplexer Modelle wie Deep Learning und Ensemble-Methoden ist das Verständnis des Entscheidungsprozesses des Modells besonders wichtig geworden. Explainable AI|XAI trägt dazu bei, Vertrauen in maschinelle Lernmodelle aufzubauen, indem es die Transparenz des Modells erhöht. Eine Verbesserung der Modelltransparenz kann durch Methoden wie den weit verbreiteten Einsatz mehrerer komplexer Modelle sowie der Entscheidungsprozesse zur Erläuterung der Modelle erreicht werden. Zu diesen Methoden gehören die Analyse der Merkmalsbedeutung, die Schätzung des Modellvorhersageintervalls, lokale Interpretierbarkeitsalgorithmen usw. Die Merkmalswichtigkeitsanalyse kann den Entscheidungsprozess des Modells erklären, indem sie den Grad des Einflusses des Modells auf die Eingabemerkmale bewertet. Schätzung des Modellvorhersageintervalls
Transparent! Eine ausführliche Analyse der Prinzipien der wichtigsten Modelle des maschinellen Lernens!
Apr 12, 2024 pm 05:55 PM
Laienhaft ausgedrückt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Eingabedaten einer vorhergesagten Ausgabe zuordnet. Genauer gesagt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Modellparameter anpasst, indem sie aus Trainingsdaten lernt, um den Fehler zwischen der vorhergesagten Ausgabe und der wahren Bezeichnung zu minimieren. Beim maschinellen Lernen gibt es viele Modelle, z. B. logistische Regressionsmodelle, Entscheidungsbaummodelle, Support-Vektor-Maschinenmodelle usw. Jedes Modell verfügt über seine anwendbaren Datentypen und Problemtypen. Gleichzeitig gibt es viele Gemeinsamkeiten zwischen verschiedenen Modellen oder es gibt einen verborgenen Weg für die Modellentwicklung. Am Beispiel des konnektionistischen Perzeptrons können wir es durch Erhöhen der Anzahl verborgener Schichten des Perzeptrons in ein tiefes neuronales Netzwerk umwandeln. Wenn dem Perzeptron eine Kernelfunktion hinzugefügt wird, kann es in eine SVM umgewandelt werden. Dieses hier
Identifizieren Sie Über- und Unteranpassung anhand von Lernkurven
Apr 29, 2024 pm 06:50 PM
In diesem Artikel wird vorgestellt, wie Überanpassung und Unteranpassung in Modellen für maschinelles Lernen mithilfe von Lernkurven effektiv identifiziert werden können. Unteranpassung und Überanpassung 1. Überanpassung Wenn ein Modell mit den Daten übertrainiert ist, sodass es daraus Rauschen lernt, spricht man von einer Überanpassung des Modells. Ein überangepasstes Modell lernt jedes Beispiel so perfekt, dass es ein unsichtbares/neues Beispiel falsch klassifiziert. Für ein überangepasstes Modell erhalten wir einen perfekten/nahezu perfekten Trainingssatzwert und einen schrecklichen Validierungssatz-/Testwert. Leicht geändert: „Ursache der Überanpassung: Verwenden Sie ein komplexes Modell, um ein einfaches Problem zu lösen und Rauschen aus den Daten zu extrahieren. Weil ein kleiner Datensatz als Trainingssatz möglicherweise nicht die korrekte Darstellung aller Daten darstellt. 2. Unteranpassung Heru.“
Die Entwicklung der künstlichen Intelligenz in der Weltraumforschung und der Siedlungstechnik
Apr 29, 2024 pm 03:25 PM
In den 1950er Jahren wurde die künstliche Intelligenz (KI) geboren. Damals entdeckten Forscher, dass Maschinen menschenähnliche Aufgaben wie das Denken ausführen können. Später, in den 1960er Jahren, finanzierte das US-Verteidigungsministerium künstliche Intelligenz und richtete Labore für die weitere Entwicklung ein. Forscher finden Anwendungen für künstliche Intelligenz in vielen Bereichen, etwa bei der Erforschung des Weltraums und beim Überleben in extremen Umgebungen. Unter Weltraumforschung versteht man die Erforschung des Universums, das das gesamte Universum außerhalb der Erde umfasst. Der Weltraum wird als extreme Umgebung eingestuft, da sich seine Bedingungen von denen auf der Erde unterscheiden. Um im Weltraum zu überleben, müssen viele Faktoren berücksichtigt und Vorkehrungen getroffen werden. Wissenschaftler und Forscher glauben, dass die Erforschung des Weltraums und das Verständnis des aktuellen Zustands aller Dinge dazu beitragen können, die Funktionsweise des Universums zu verstehen und sich auf mögliche Umweltkrisen vorzubereiten
Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Zu den häufigsten Herausforderungen, mit denen Algorithmen für maschinelles Lernen in C++ konfrontiert sind, gehören Speicherverwaltung, Multithreading, Leistungsoptimierung und Wartbarkeit. Zu den Lösungen gehören die Verwendung intelligenter Zeiger, moderner Threading-Bibliotheken, SIMD-Anweisungen und Bibliotheken von Drittanbietern sowie die Einhaltung von Codierungsstilrichtlinien und die Verwendung von Automatisierungstools. Praktische Fälle zeigen, wie man die Eigen-Bibliothek nutzt, um lineare Regressionsalgorithmen zu implementieren, den Speicher effektiv zu verwalten und leistungsstarke Matrixoperationen zu nutzen.
Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Übersetzer |. Rezensiert von Li Rui |. Chonglou Modelle für künstliche Intelligenz (KI) und maschinelles Lernen (ML) werden heutzutage immer komplexer, und die von diesen Modellen erzeugten Ergebnisse sind eine Blackbox, die den Stakeholdern nicht erklärt werden kann. Explainable AI (XAI) zielt darauf ab, dieses Problem zu lösen, indem es Stakeholdern ermöglicht, die Funktionsweise dieser Modelle zu verstehen, sicherzustellen, dass sie verstehen, wie diese Modelle tatsächlich Entscheidungen treffen, und Transparenz in KI-Systemen, Vertrauen und Verantwortlichkeit zur Lösung dieses Problems gewährleistet. In diesem Artikel werden verschiedene Techniken der erklärbaren künstlichen Intelligenz (XAI) untersucht, um ihre zugrunde liegenden Prinzipien zu veranschaulichen. Mehrere Gründe, warum erklärbare KI von entscheidender Bedeutung ist. Vertrauen und Transparenz: Damit KI-Systeme allgemein akzeptiert und vertrauenswürdig sind, müssen Benutzer verstehen, wie Entscheidungen getroffen werden
Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Maschinelles Lernen ist ein wichtiger Zweig der künstlichen Intelligenz, der Computern die Möglichkeit gibt, aus Daten zu lernen und ihre Fähigkeiten zu verbessern, ohne explizit programmiert zu werden. Maschinelles Lernen hat ein breites Anwendungsspektrum in verschiedenen Bereichen, von der Bilderkennung und der Verarbeitung natürlicher Sprache bis hin zu Empfehlungssystemen und Betrugserkennung, und es verändert unsere Lebensweise. Im Bereich des maschinellen Lernens gibt es viele verschiedene Methoden und Theorien, von denen die fünf einflussreichsten Methoden als „Fünf Schulen des maschinellen Lernens“ bezeichnet werden. Die fünf Hauptschulen sind die symbolische Schule, die konnektionistische Schule, die evolutionäre Schule, die Bayes'sche Schule und die Analogieschule. 1. Der Symbolismus, auch Symbolismus genannt, betont die Verwendung von Symbolen zum logischen Denken und zum Ausdruck von Wissen. Diese Denkrichtung glaubt, dass Lernen ein Prozess der umgekehrten Schlussfolgerung durch das Vorhandene ist
Ist Flash Attention stabil? Meta und Harvard stellten fest, dass die Gewichtsabweichungen ihrer Modelle um Größenordnungen schwankten
May 30, 2024 pm 01:24 PM
MetaFAIR hat sich mit Harvard zusammengetan, um einen neuen Forschungsrahmen zur Optimierung der Datenverzerrung bereitzustellen, die bei der Durchführung groß angelegten maschinellen Lernens entsteht. Es ist bekannt, dass das Training großer Sprachmodelle oft Monate dauert und Hunderte oder sogar Tausende von GPUs verwendet. Am Beispiel des Modells LLaMA270B erfordert das Training insgesamt 1.720.320 GPU-Stunden. Das Training großer Modelle stellt aufgrund des Umfangs und der Komplexität dieser Arbeitsbelastungen einzigartige systemische Herausforderungen dar. In letzter Zeit haben viele Institutionen über Instabilität im Trainingsprozess beim Training generativer SOTA-KI-Modelle berichtet. Diese treten normalerweise in Form von Verlustspitzen auf. Beim PaLM-Modell von Google kam es beispielsweise während des Trainingsprozesses zu Instabilitäten. Numerische Voreingenommenheit ist die Hauptursache für diese Trainingsungenauigkeit.
