Ist die Gleichung ein binärer Baumwald? Entdecken Sie unbekannte maßgebliche Gleichungen und physikalische Mechanismen direkt aus Daten

Forscher hoffen, mithilfe maschineller Lernmethoden automatisch die wertvollsten und wichtigsten intrinsischen Gesetze direkt aus hochdimensionalen nichtlinearen Daten zu extrahieren (d. h. die PDE-basierten maßgeblichen Gleichungen hinter dem Problem zu extrahieren), um eine automatische Wissensentdeckung zu erreichen.

Kürzlich haben Forschungsteams des Eastern Institute of Technology, der University of Washington, des Ruilai Intelligence und der Peking University einen genetischen Algorithmus SGA-PDE vorgeschlagen, der auf symbolischer Mathematik basiert und einen offenen Kandidatensatz erstellt, der jede Form direkt aus der Datenkontrolle extrahieren kann Gleichung.

Experimente zeigen, dass SGA-PDE nicht nur die Burgers-Gleichung (mit Interaktionstermen), die Korteweg-de-Vries-Gleichung (KdV, mit Ableitungstermen höherer Ordnung) und die Chafee-Infante-Gleichung (mit Exponentialtermen und Ableitung) ermitteln kann Terme) aus Daten) und ermittelte auch erfolgreich die maßgeblichen Gleichungen mit zusammengesetzten Funktionen und Gleichungen mit gebrochenen Strukturen im Problem der viskosen Schwerkraftströmung, wobei die beiden letztgenannten mit früheren Methoden schwer zu entdecken waren. SGA-PDE ist nicht auf Vorkenntnisse über die Gleichungsform angewiesen und füllt die Lücke bei komplexen Gleichungsgewinnungsproblemen zur Strukturkontrolle. Dieses Modell erfordert nicht die Angabe eines Kandidatengleichungssatzes im Voraus, was für die praktische Anwendung automatischer Wissenserkennungsalgorithmen bei unbekannten wissenschaftlichen Problemen von Vorteil ist.

Die Studie mit dem Titel „Symbolischer genetischer Algorithmus zur Entdeckung offener partieller Differentialgleichungen (SGA-PDE)“ wurde am 1. Juni in Physical Review Research veröffentlicht.

Die aktuelle Idee zur Entdeckung allgemeiner Kenntnisse besteht darin, eine spärliche Regression zu verwenden, d. FINDEN. Diese Art von Methode erfordert jedoch, dass der Benutzer die grobe Form der Gleichung im Voraus bestimmt und dann alle entsprechenden Differentialoperatoren als Funktionsterme im Kandidatensatz angibt. Funktionsterme, die im Kandidatensatz nicht vorhanden sind, können nicht gefunden werden aus den Daten. Einige der neuesten Forschungsarbeiten versuchen, genetische Algorithmen zu verwenden, um Kandidatenmengen zu erweitern, aber es gibt erhebliche Einschränkungen bei der Rekombination und Mutation von Genen, und es ist immer noch unmöglich, komplexe Strukturfunktionsterme (wie Bruchstrukturen und zusammengesetzte Funktionen) direkt aus den Daten zu generieren Der Schlüssel zu maßgebenden Gleichungen in offener Form liegt darin, jede Form von maßgebenden Gleichungen auf einfach zu berechnende Weise zu generieren und darzustellen und die Genauigkeit der Gleichungsform zu bewerten, indem gemessen wird, wie gut die erzeugten Gleichungen zu den beobachteten Daten passen Führen Sie dann Experimente mit den ermittelten Gleichungen durch. Daher sind Darstellung und Optimierung die Kernthemen der automatischen Wissensermittlung.

Tabelle 1. Vergleichstabelle der automatischen Kontrollgleichungs-Mining-Methoden

Die Herausforderung bei der Darstellung des Problems ist:

1. Wie man begrenzte Grundeinheiten verwendet, um unendlich komplexe strukturelle Kontrollgleichungen darzustellen (d. h. offene Kandidatenmenge)

; 2. So erstellen Sie eine einfach zu berechnende Kontrollgleichungsdarstellung. Um Gleichungen beliebiger Struktur frei ausdrücken zu können, haben die Forscher die grundlegende Darstellungseinheit von SGA-PDE auf Operanden und Operatoren abgeschwächt und Binärbäume verwendet, um durch symbolische Mathematik eine offene Kandidatenmenge zu konstruieren.

Die Herausforderungen des Optimierungsproblems sind: 1. Der Gradient zwischen der Gleichungsform und dem Gleichungsbewertungsindex ist schwer zu berechnen. 2 Der zulässige Bereich der offenen Kandidatenmenge ist schwierig Optimierungsprozess, um Exploration und Nutzung (Ausbeutung) effektiv in Einklang zu bringen. Um das Problem der offenen Kandidatenmenge effizient zu optimieren, verwendeten die Forscher einen genetischen Algorithmus, der speziell für Baumstrukturen entwickelt wurde, um eine Optimierung in Form von Gleichungen zu erreichen.

Abbildung 1: Schematische Darstellung des automatischen Wissenserkennungsproblems und der SGA-PDE Darstellungsmaßstab der Gleichung von Die unabhängige Funktionstermebene wird in eine einfachere Operator- und Operandenebene umgewandelt.

SGA-PDE unterteilt die Operatoren in der Kontrollgleichung in Doppeloperatoren (z. B. +, -) und Einzeloperatoren (z. B. sin, cos) und definiert dann alle potenziellen Variablen als Operanden (z. B. x, t, u). Forscher nutzen die Struktur eines Binärbaums, um Operatoren und Operanden zu kombinieren und so verschiedene Gleichungen zu kodieren. Alle Endknoten (Blattknoten mit Grad 0) im Binärbaum entsprechen Operanden, und alle Nicht-Terminalknoten entsprechen Operatoren. Doppeloperatoren entsprechen Knoten mit Grad 2 und Einzeloperatoren entsprechen Knoten mit Grad 1.

Wie in Abbildung 2 gezeigt, kann jeder Funktionsterm durch eine berechenbare Zeichenfolge in einen Binärbaum umgewandelt werden Gleichzeitig kann ein Binärbaum, der bestimmte mathematische Regeln erfüllt, auch in eine Funktion umgewandelt werden Begriff. Darüber hinaus entspricht eine maßgebliche Gleichung mit mehreren Funktionstermen einem Wald , der aus mehreren Binärbäumen besteht. SGA-PDE repräsentiert jede offene partielle Differentialgleichung durch symbolische Mathematik. Darüber hinaus wird in dem Artikel auch eine Methode zur zufälligen Generierung von Binärbäumen mit mathematischer Bedeutung vorgeschlagen, mit der sichergestellt werden kann, dass die generierten Binärbäume nicht gegen mathematische Prinzipien verstoßen.

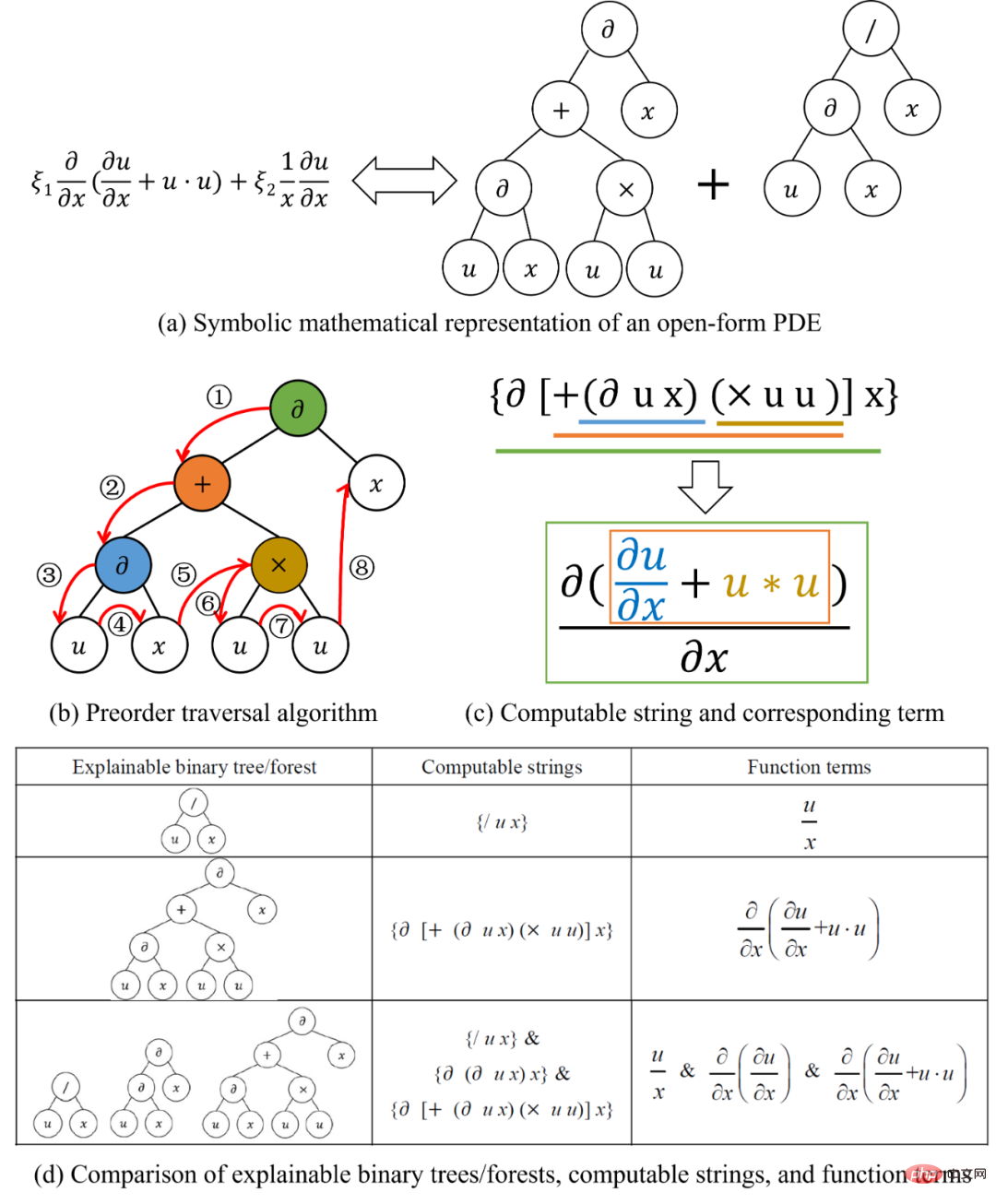
Abbildung 2: Darstellungs- und Transformationsmethode zwischen Binärbäumen und Funktionstermen

Da die in Abbildung 2 gezeigte Darstellungsmethode eine Eins-zu-Eins-Entsprechung zwischen Stichproben im Funktionsraum und Stichproben im Binärbaumraum ermöglicht . Dies bedeutet, dass auf symbolischer Mathematik basierende Darstellungen effizient und nicht redundant sind und als Kodierungsprozesse in genetischen Algorithmen verwendet werden können. Die Forscher schlugen einen genetischen Algorithmus für Baumstrukturen vor (Abbildung 3), um automatisch Kontrollgleichungen zu ermitteln, die mit beobachteten Daten aus experimentellen Daten übereinstimmen. Dieser genetische Algorithmus für Baumstrukturen kann eine Optimierung auf verschiedenen Ebenen erreichen. Der Reorganisationslink wird auf Waldebene (Gleichungsebene) optimiert, um die optimale Kombination von Binärbäumen (Funktionstermen) zu finden. Dieser Link ähnelt der aktuellen gängigen Methode der Sparse-Regression, bei der es sich um eine Optimierung innerhalb eines geschlossenen Kandidatensatzes handelt.

Der Mutationslink wird auf der Ebene des Binärbaums (Funktionsterm) optimiert Durch zufälliges Generieren verschiedener Knotenattribute finden wir die optimale Kombination von Knotenattributen unter einer bestimmten Binärbaumstruktur . ).

Der Ersatzlink wird auch auf der Ebene des Binärbaums (Funktionsterm) optimiert, generiert jedoch eine neue Binärbaumstruktur, die eine Erkundung der Baumstruktur darstellt und die Optimierung eines vollständig offenen Kandidatensatzes realisiert.

SGA-PDE kann die Nutzung und Erforschung der binären Baumtopologie durch mehrstufige Optimierung berücksichtigen, was dazu beiträgt, die optimale Gleichungsform effizient zu finden.

Abbildung 3: Genetischer Algorithmus für die Baumstruktur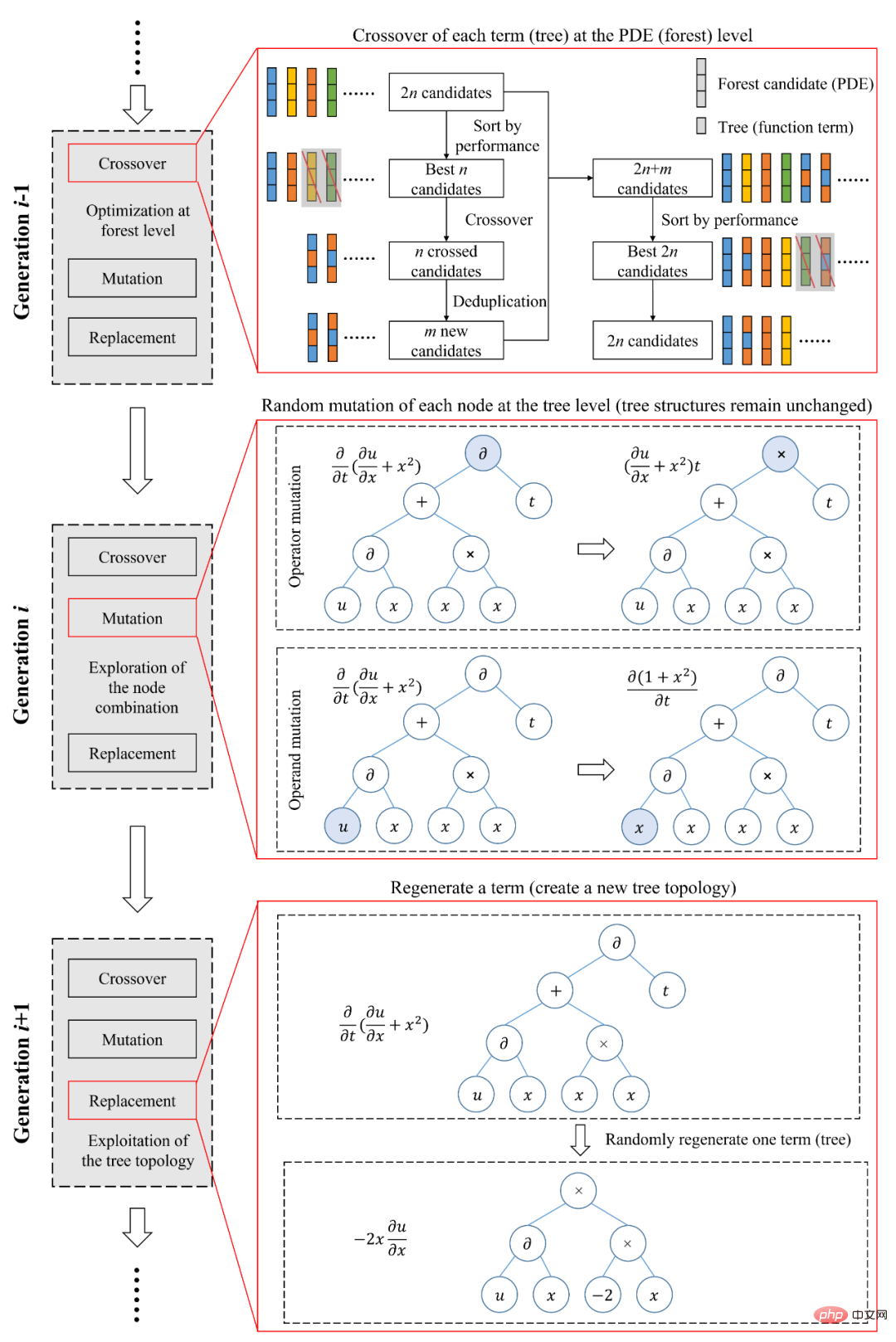

Die experimentellen Daten sind in Abbildung 4 dargestellt, wobei Spalte 2 die physikalischen Feldbeobachtungen zeigt, die einzigen Eingabeinformationen für SGA-PDE sind. Die zugrunde liegenden ersten Ableitungen in den Spalten 3 und 4 können durch Differenzierung der physikalischen Feldbeobachtungen erhalten werden. Spalte 1 ist die korrekte Form der Gleichung. Im Experiment verwendet SGA-PDE dieselben voreingestellten Operanden und Operatoren und muss nicht an bestimmte Probleme angepasst werden, um die Vielseitigkeit des Algorithmus zu überprüfen.

Schließlich hat SGA-PDE erfolgreich die Burgers-Gleichung, die KdV-Gleichung, die Chafee-Infante-Gleichung, die viskose Schwerkraftströmungsgleichung mit zusammengesetzter Funktionsableitung und Gleichungen mit Bruchstruktur aus den Daten ermittelt. Die obige Gleichung hat viele komplexe Formen wie Exponentialterme, Ableitungsterme höherer Ordnung, Interaktionsterme, zusammengesetzte Funktionen und verschachtelte Strukturen.

Tabelle 2 vergleicht die Berechnungsergebnisse verschiedener vorhandener Algorithmen in den oben genannten fünf Berechnungsbeispielen. Es ist ersichtlich, dass SGA-PDE die Lücke beim Mining der Kontrollgleichungen komplexer Strukturen füllt.

Abbildung 4: Experimentelle Datengrafik

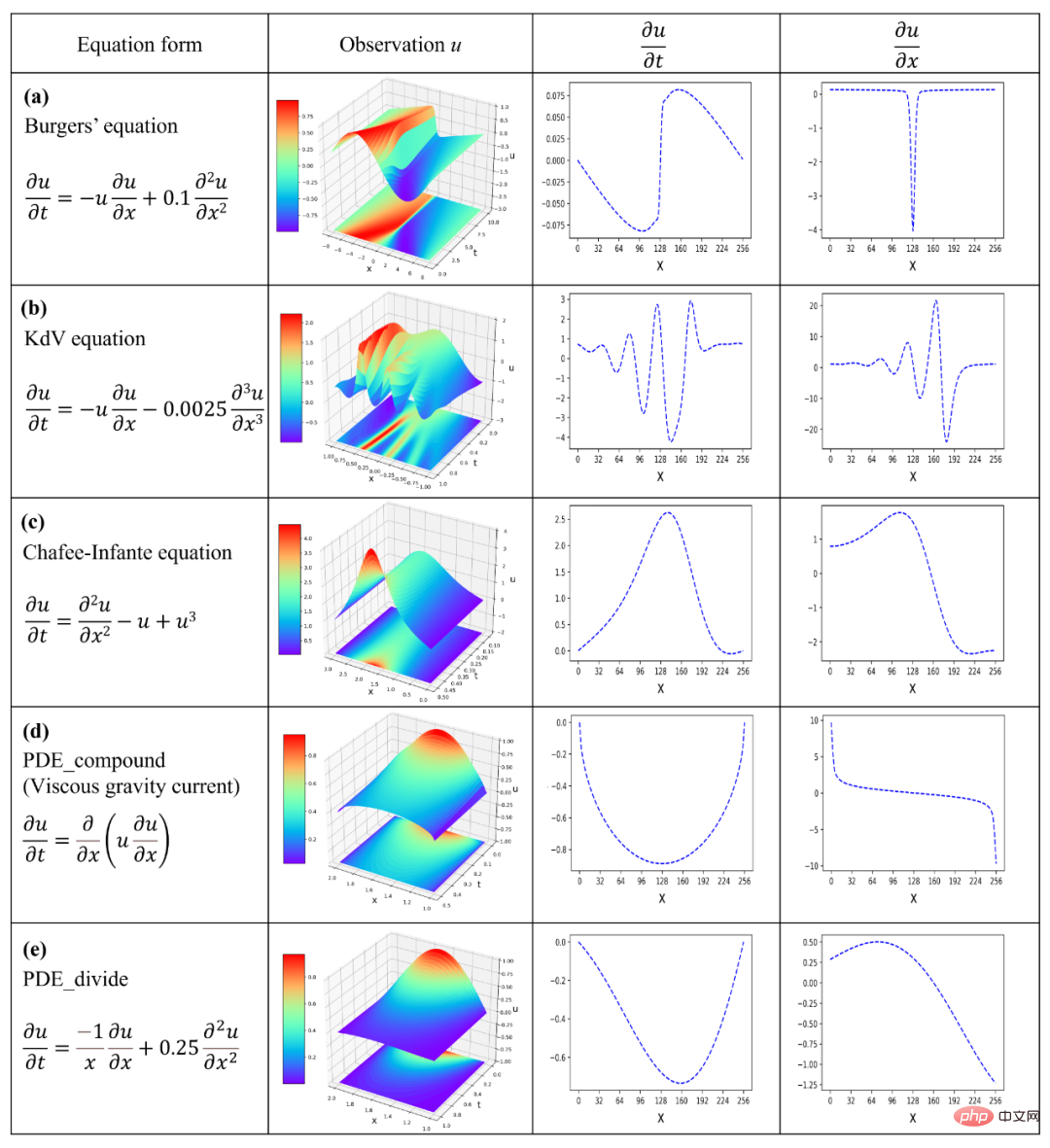
Tabelle 2 Experimentelle Ergebnisse des automatischen Wissenserkennungsalgorithmus bei verschiedenen Problemen beim Mining von Kontrollgleichungen

Um den Optimierungsprozess von SGA-PDE besser zu verstehen, zeigt Abbildung 5 den Entwicklungspfad beim Mining der KdV-Gleichung. Es ist ersichtlich, dass die von der ersten Generation generierte optimale Gleichung weit von der tatsächlichen Gleichung entfernt ist. Im darauffolgenden Evolutionsprozess mit den Veränderungen in der topologischen Struktur des Binärbaums und der Bedeutung der Knoten sowie der Kreuzrekombination zwischen Funktionstermen wurde schließlich in der 31. Generation und zu diesem Zeitpunkt die richtige Lösung gefunden Der AIC-Index hat die im Artikelstandard angegebene Konvergenz erreicht. Interessanterweise wird, wenn die Optimierung fortgesetzt wird, bei Generation 69 ein sparsamerer Ausdruck der KdV-Gleichung gefunden, der auf der Ableitung einer zusammengesetzten Funktion basiert. Abbildung 6 zeigt den Optimierungsprozess von SGA-PDE, um die maßgeblichen Gleichungen mit gebrochener Struktur zu finden.

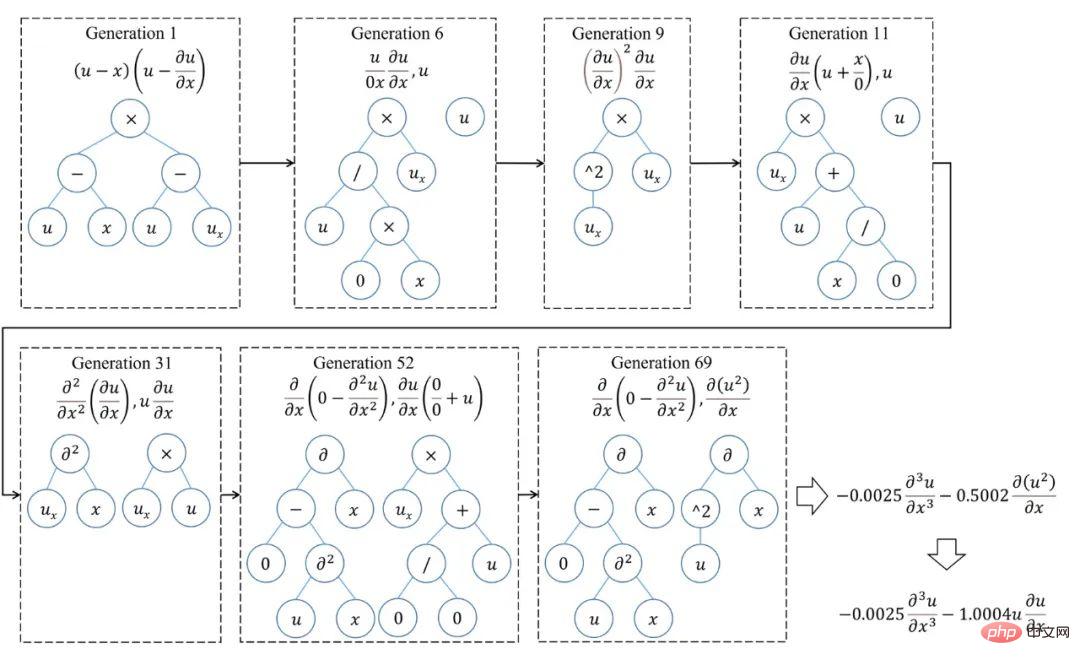
Abbildung 5: Optimierungsprozess von SGA-PDE für die KdV-Gleichung

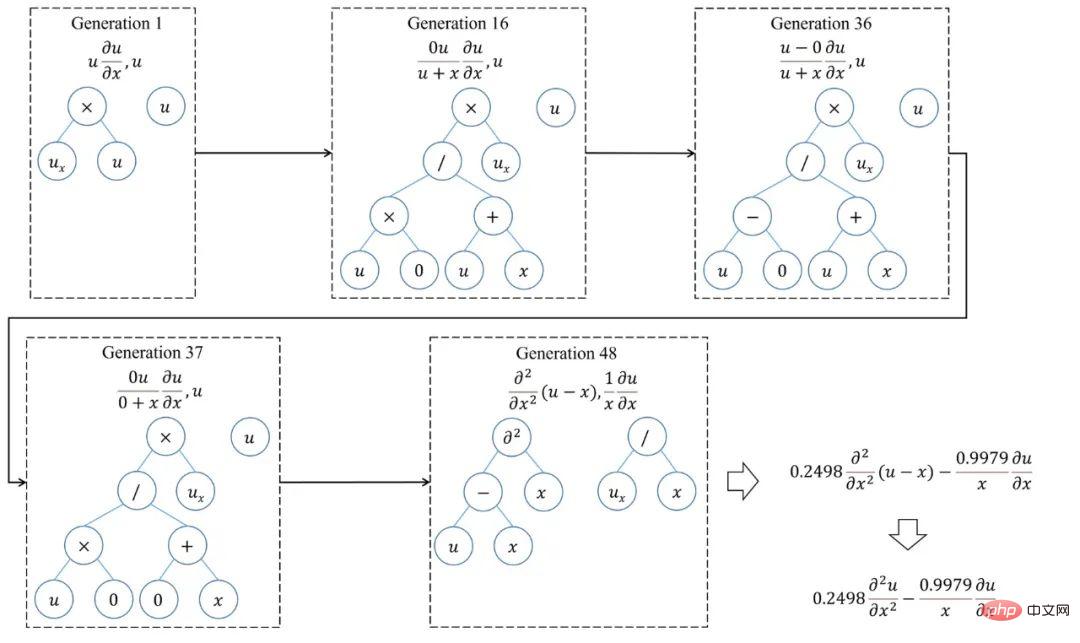
Abbildung 6: Optimierungsprozess von SGA-PDE für Gleichungen mit gebrochener Struktur

Die Kontrollgleichungen sind Domänenwissen. Eine effiziente Darstellung Allerdings sind die Gleichungsparameter und sogar Gleichungsformen vieler realer Probleme unsicher, was es schwierig macht, genaue Kontrollgleichungen zu schreiben, was die Anwendung von Domänenwissen beim maschinellen Lernen stark einschränkt.

SGA-PDE nutzt symbolische Mathematik zur Transformation von Gleichungen und löst das Problem der Darstellung jeder Form partieller Differentialgleichungen. Darüber hinaus verwendet SGA-PDE einen genetischen Algorithmus, der für Binärbäume entwickelt wurde, und ermittelt durch iterative Optimierung der Topologie und Knotenattribute des Baums automatisch Kontrollgleichungen , die zu den Beobachtungsdaten aus dem offenen Bereich passen. Bei der Optimierung ist SGA-PDE weder auf vorherige Informationen in Form von Gleichungen angewiesen, noch muss ein Kandidatensatz angegeben werden, wodurch eine automatische Optimierung komplexer Strukturgleichungen realisiert wird. Gleichzeitig ist SGA-PDE auch ein Algorithmus ohne Gradienten, der das Problem der schwierigen Berechnung des Gradienten zwischen der Gleichungsstruktur und dem Verlustwert vermeidet. Zukünftige Forschung wird sich auf Folgendes konzentrieren: 1. Versuchen Sie, verstärkende Lern- oder kombinatorische Optimierungsalgorithmen zu kombinieren; 2. Reduzieren Sie den Lösungsraum durch Einbettung physikalischer Mechanismen; . Integrieren Sie Methoden zur Wissenseinbettung und Wissensentdeckung.

Papierlink (kostenlos verfügbar):

https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.4.023174

Code- und Beispieldatenlink:

https://github.com/ YuntianChen /SGA-PDE

Das obige ist der detaillierte Inhalt vonIst die Gleichung ein binärer Baumwald? Entdecken Sie unbekannte maßgebliche Gleichungen und physikalische Mechanismen direkt aus Daten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!