
In diesem Artikel geht es um die Arbeit des tiefen Verstärkungslernens, um Angriffen zu widerstehen. In diesem Artikel untersucht der Autor die Robustheit von Deep-Reinforcement-Learning-Strategien gegenüber gegnerischen Angriffen aus der Perspektive einer robusten Optimierung. Im Rahmen der robusten Optimierung wird der optimale gegnerische Angriff durch die Minimierung der erwarteten Rendite der Strategie erreicht, und dementsprechend wird ein guter Abwehrmechanismus durch die Verbesserung der Leistung der Strategie bei der Bewältigung des Worst-Case-Szenarios erreicht.
Angesichts der Tatsache, dass Angreifer in der Trainingsumgebung normalerweise nicht angreifen können, schlägt der Autor einen gierigen Angriffsalgorithmus vor, der versucht, die erwartete Rendite der Strategie zu minimieren, ohne mit der Umgebung zu interagieren. Darüber hinaus schlägt der Autor auch einen Verteidigungsalgorithmus vor ein Max-Min-Spiel zur Durchführung eines kontradiktorischen Trainings von Deep-Reinforcement-Learning-Algorithmen.
Experimentelle Ergebnisse in der Atari-Spielumgebung zeigen, dass der vom Autor vorgeschlagene gegnerische Angriffsalgorithmus effektiver ist als der bestehende Angriffsalgorithmus und die Strategie-Return-Rate schlechter ist. Die durch den im Artikel vorgeschlagenen gegnerischen Verteidigungsalgorithmus generierten Strategien sind gegenüber einer Reihe gegnerischer Angriffe robuster als bestehende Verteidigungsmethoden.
Bei einer gegebenen Probe (x, y) und einem neuronalen Netzwerk f lautet das Optimierungsziel für die Generierung einer gegnerischen Probe:
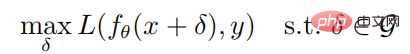
Wo ist der Parameter des neuronalen Netzwerks f, L ist Die Verlustfunktion ist eine Reihe kontradiktorischer Störungen und  ist eine normbeschränkte Kugel mit x als Mittelpunkt und Radius als Radius. Die Berechnungsformel zum Generieren gegnerischer Proben durch PGD-Angriff lautet wie folgt:
ist eine normbeschränkte Kugel mit x als Mittelpunkt und Radius als Radius. Die Berechnungsformel zum Generieren gegnerischer Proben durch PGD-Angriff lautet wie folgt:
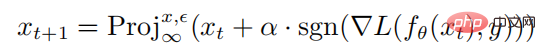
wobei  die Projektionsoperation darstellt. Wenn die Eingabe außerhalb der Normkugel liegt, wird die Eingabe auf die Kugel mit x-Mittelpunkt als Radius projiziert Mittelwert ist die einstufige Störungsgröße des PGD-Angriffs.
die Projektionsoperation darstellt. Wenn die Eingabe außerhalb der Normkugel liegt, wird die Eingabe auf die Kugel mit x-Mittelpunkt als Radius projiziert Mittelwert ist die einstufige Störungsgröße des PGD-Angriffs.
2.2 Reinforcement Learning und Policy Gradients
Ein Problem des Reinforcement Learning kann als Markov-Entscheidungsprozess beschrieben werden. Der Markov-Entscheidungsprozess kann als 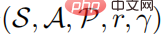 -Fünffach definiert werden, wobei S einen Zustandsraum darstellt, A einen Aktionsraum darstellt,
-Fünffach definiert werden, wobei S einen Zustandsraum darstellt, A einen Aktionsraum darstellt, 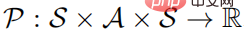 die Zustandsübergangswahrscheinlichkeit darstellt, r die Belohnungsfunktion darstellt und den Abzinsungsfaktor darstellt. Das Ziel des starken Lernlernens besteht darin, eine Parameterrichtlinienverteilung
die Zustandsübergangswahrscheinlichkeit darstellt, r die Belohnungsfunktion darstellt und den Abzinsungsfaktor darstellt. Das Ziel des starken Lernlernens besteht darin, eine Parameterrichtlinienverteilung  zu lernen, um die Wertefunktion
zu lernen, um die Wertefunktion
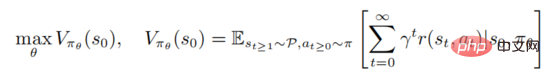
zu maximieren, wobei der Anfangszustand dargestellt wird. Starkes Lernen beinhaltet die Bewertung der Aktionswertfunktion
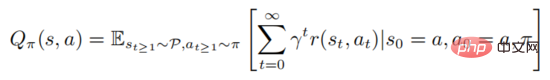
Die obige Formel beschreibt die mathematische Erwartung, der Richtlinie nach der Ausführung des Staates Folge zu leisten. Aus der Definition ist ersichtlich, dass die Wertfunktion und die Aktionswertfunktion die folgende Beziehung erfüllen:
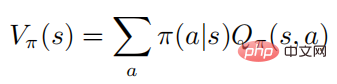
Der Einfachheit halber konzentriert sich der Autor hauptsächlich auf den Markov-Prozess des diskreten Aktionsraums, jedoch auf alle Algorithmen und Ergebnisse Kann sicherlich direkt auf kontinuierliche Einstellungen angewendet werden.
Der gegnerische Angriff und die Verteidigung der Deep Reinforcement Learning-Strategie basieren auf dem Rahmen der robusten Optimierung PGD
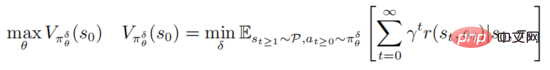
wobei  steht, die Menge der gegnerischen Störungssequenzen
steht, die Menge der gegnerischen Störungssequenzen  darstellt und für alle
darstellt und für alle 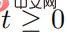 erfüllt
erfüllt 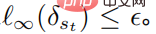 Die obige Formel bietet einen einheitlichen Rahmen für tiefgreifendes Verstärkungslernen zur Bekämpfung von Angriffen und Verteidigungen.
Die obige Formel bietet einen einheitlichen Rahmen für tiefgreifendes Verstärkungslernen zur Bekämpfung von Angriffen und Verteidigungen.
Einerseits sucht die interne Minimierungsoptimierung nach kontradiktorischen Störungssequenzen, die dazu führen, dass die aktuelle Strategie falsche Entscheidungen trifft. Andererseits besteht der Zweck der externen Maximierung darin, die Strategieverteilungsparameter zu finden, um die erwartete Rendite im Rahmen der Störungsstrategie zu maximieren. Nach den oben genannten gegnerischen Angriffen und Verteidigungsspielen sind die Strategieparameter während des Trainingsprozesses widerstandsfähiger gegen gegnerische Angriffe.
Der Zweck der internen Minimierung der Zielfunktion besteht darin, gegnerische Störungen zu erzeugen. Für verstärkende Lernalgorithmen ist das Erlernen der optimalen gegnerischen Störungen jedoch sehr zeitaufwändig und arbeitsintensiv, und da die Trainingsumgebung eine Black Box ist Angreifer. In diesem Artikel betrachtet der Autor daher eine praktische Situation, in der der Angreifer Störungen in verschiedenen Zuständen einfügt. Im Szenario des überwachten Lernangriffs muss der Angreifer nur das Klassifikatormodell austricksen, um es falsch zu klassifizieren und falsche Bezeichnungen zu erzeugen. Im Szenario des verstärkenden Lernangriffs stellt die Aktionswertfunktion dem Angreifer zusätzliche Informationen, d. h. einen kleinen Verhaltenswert, zur Verfügung Dies führt zu einer geringen erwarteten Rendite. Dementsprechend definiert der Autor die optimale gegnerische Störung beim Deep Reinforcement Learning wie folgt:
Definition 1: Eine optimale gegnerische Störung auf Zustände s kann die erwartete Rückkehr des Zustands minimieren
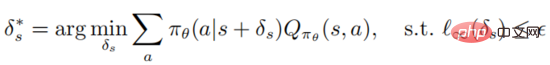
Es ist zu beachten, dass die Optimierung die obige Formel löst Es muss sichergestellt werden, dass der Angreifer den Agenten dazu verleiten kann, das schlechteste Entscheidungsverhalten zu wählen. Die Aktionswertfunktion des Agenten ist dem Angreifer jedoch nicht bekannt, sodass es keine Garantie dafür gibt, dass die gegnerische Störung optimal ist . Der folgende Satz kann zeigen, dass bei optimaler Richtlinie die optimale gegnerische Störung ohne Zugriff auf die Aktionswertfunktion erzeugt werden kann
Theorem 1: Wenn die Kontrollstrategie 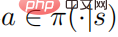 optimal ist, erfüllen die Aktionswertfunktion und die Richtlinie die folgende Beziehung
optimal ist, erfüllen die Aktionswertfunktion und die Richtlinie die folgende Beziehung
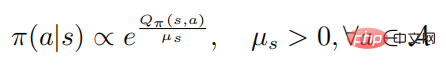
Wobei es die Richtlinienentropie darstellt, eine zustandsabhängige Konstante ist und sich bei Änderung auf 0 auch auf 0 ändert. Anschließend beweist die folgende Formel
: Wenn die Zufallsstrategie 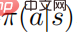 das Optimum erreicht Die Wertfunktion
das Optimum erreicht Die Wertfunktion 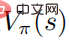 erreicht ebenfalls das Optimum, was bedeutet, dass in jedem Zustand keine andere Verhaltensverteilung gefunden werden kann, die zu einer Erhöhung der Wertfunktion
erreicht ebenfalls das Optimum, was bedeutet, dass in jedem Zustand keine andere Verhaltensverteilung gefunden werden kann, die zu einer Erhöhung der Wertfunktion 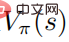 führt. Dementsprechend kann bei gegebener optimaler Aktionswertfunktion
führt. Dementsprechend kann bei gegebener optimaler Aktionswertfunktion 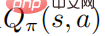 die optimale Strategie
die optimale Strategie 
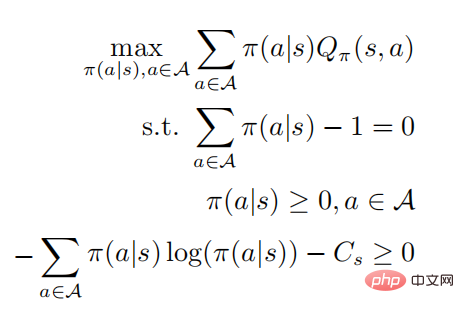
durch Lösen des eingeschränkten Optimierungsproblems erhalten werden. Die zweite und dritte Zeile geben an, dass es sich um eine Wahrscheinlichkeitsverteilung handelt, und die letzte Zeile gibt an, dass es sich um eine Strategie handelt Gemäß den KKT-Bedingungen kann das obige Optimierungsproblem in die folgende Form umgewandelt werden:
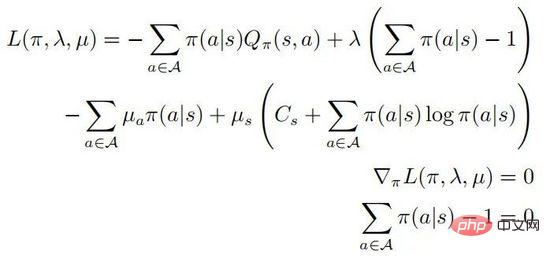
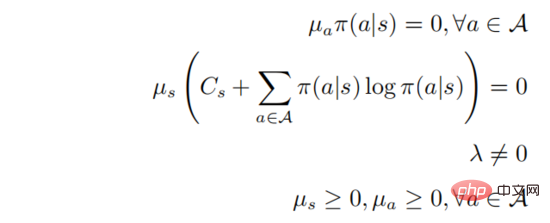
Unter ihnen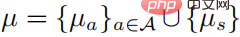 . Nehmen wir an, dass
. Nehmen wir an, dass 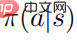 für alle Verhaltensweisen
für alle Verhaltensweisen 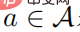 positiv definit ist, dann gilt:
positiv definit ist, dann gilt:
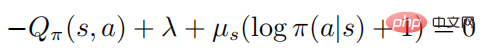
Wenn 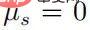 , dann muss es
, dann muss es 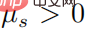 geben, und dann gibt es für jedes
geben, und dann gibt es für jedes 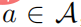
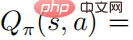 , damit wir die Beziehung zwischen dem Aktionswert erhalten können Funktion und der Softmax der Strategie
, damit wir die Beziehung zwischen dem Aktionswert erhalten können Funktion und der Softmax der Strategie
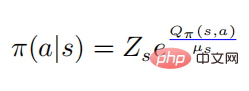
darunter  , und dann haben wir
, und dann haben wir
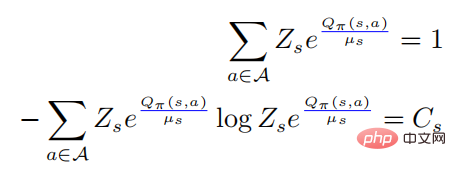
Wenn wir die obige erste Gleichung in die zweite bringen, haben wir
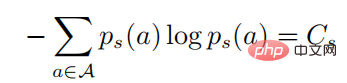
darunter
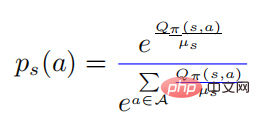
In der obigen Formel bedeutet 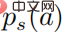 Eine Wahrscheinlichkeitsverteilung in Form eines Softmax mit einer Entropie von . Wenn es gleich 0 ist, wird es auch 0. In diesem Fall ist es größer als 0, dann zu diesem Zeitpunkt
Eine Wahrscheinlichkeitsverteilung in Form eines Softmax mit einer Entropie von . Wenn es gleich 0 ist, wird es auch 0. In diesem Fall ist es größer als 0, dann zu diesem Zeitpunkt  .
.
Satz 1 zeigt, dass bei optimaler Richtlinie die optimale Störung durch Maximierung der Kreuzentropie der gestörten Richtlinie und der ursprünglichen Richtlinie erreicht werden kann. Der Einfachheit halber bezeichnet der Autor den Angriff von Theorem 1 als strategischen Angriff und verwendet das PGD-Algorithmus-Framework, um den optimalen strategischen Angriff zu berechnen. Das spezifische Algorithmus-Flussdiagramm ist in Algorithmus 1 unten dargestellt.

Das Flussdiagramm des vom Autor vorgeschlagenen robusten Optimierungsalgorithmus zur Abwehr von Störungen ist in Algorithmus 2 unten dargestellt. Dieser Algorithmus wird als strategisches Angriffsgegnertraining bezeichnet. Während der Trainingsphase wird die Störungsrichtlinie verwendet, um mit der Umgebung zu interagieren, und gleichzeitig wird geschätzt, dass die Aktionswertfunktion 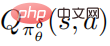 der Störungsrichtlinie das Richtlinientraining unterstützt.
der Störungsrichtlinie das Richtlinientraining unterstützt.
Die konkreten Details sind, dass der Autor zunächst strategische Angriffe einsetzt, um Störungen während der Trainingsphase zu erzeugen, auch wenn eine Reduzierung der Wertfunktion nicht garantiert werden kann. In den frühen Phasen des Trainings hängt die Richtlinie möglicherweise nicht mit der Aktionswertfunktion zusammen. Mit fortschreitendem Training wird die Softmax-Beziehung schrittweise erfüllt.
Andererseits müssen die Autoren die Aktionswertfunktion 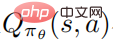 genau schätzen, was schwierig zu handhaben ist, da die Trajektorien durch die Ausführung der gestörten Richtlinie erfasst werden und die Verwendung dieser Daten zur Schätzung der Aktionswertfunktion der ungestörten Richtlinie sehr schwierig sein kann ungenau.
genau schätzen, was schwierig zu handhaben ist, da die Trajektorien durch die Ausführung der gestörten Richtlinie erfasst werden und die Verwendung dieser Daten zur Schätzung der Aktionswertfunktion der ungestörten Richtlinie sehr schwierig sein kann ungenau.

Die Zielfunktion der optimierten Störungsstrategie 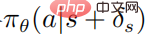 unter Verwendung von PPO ist
unter Verwendung von PPO ist
wobei 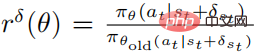 und
und 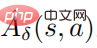 eine Schätzung der Durchschnittsfunktion
eine Schätzung der Durchschnittsfunktion 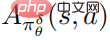 der Störungsstrategie ist. In der Praxis wird
der Störungsstrategie ist. In der Praxis wird 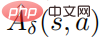 nach der Methode GAE geschätzt. Das spezifische Algorithmus-Flussdiagramm ist in der folgenden Abbildung dargestellt.
nach der Methode GAE geschätzt. Das spezifische Algorithmus-Flussdiagramm ist in der folgenden Abbildung dargestellt.

Die drei Unterabbildungen rechts unten zeigen die Ergebnisse verschiedener Angriffsstörungen. Es kann festgestellt werden, dass sowohl die umgekehrt trainierte Richtlinie als auch die Standardrichtlinie resistent gegen zufällige Störungen sind. Im Gegensatz dazu beeinträchtigen gegnerische Angriffe die Leistung verschiedener Strategien. Die Ergebnisse hängen von der Testumgebung und dem Verteidigungsalgorithmus ab. Darüber hinaus lässt sich feststellen, dass die Leistungslücke zwischen den drei gegnerischen Angriffsalgorithmen gering ist.
Im Gegensatz dazu führt die von den Autoren des Papiers vorgeschlagene Strategie zur Bekämpfung von Algorithmusinterferenzen in relativ schwierigen Situationen zu viel geringeren Erträgen. Insgesamt liefert der in der Arbeit vorgeschlagene strategische Angriffsalgorithmus in den meisten Fällen die geringste Belohnung, was darauf hindeutet, dass er tatsächlich der effizienteste aller getesteten gegnerischen Angriffsalgorithmen ist.

Wie in der folgenden Abbildung dargestellt, werden die Lernkurven verschiedener Verteidigungsalgorithmen und Standard-PPO dargestellt. Es ist wichtig zu beachten, dass die Leistungskurve lediglich die erwartete Rendite der zur Interaktion mit der Umgebung verwendeten Strategie darstellt. Unter allen Trainingsalgorithmen weist der in der Arbeit vorgeschlagene ATPA die geringste Trainingsvarianz auf und ist daher stabiler als andere Algorithmen. Beachten Sie auch, dass ATPA viel langsamer voranschreitet als Standard-PPO, insbesondere in den frühen Trainingsphasen. Dies führt dazu, dass das Strategietraining in den frühen Trainingsphasen durch Störungen durch ungünstige Faktoren sehr instabil werden kann. Die Tabelle
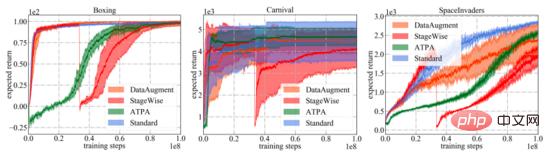
fasst die erwarteten Renditen von Strategien zusammen, die unterschiedliche Algorithmen unter unterschiedlichen Störungen verwenden. Es kann festgestellt werden, dass ATPA-trainierte Strategien gegenüber verschiedenen gegnerischen Eingriffen resistent sind. Im Vergleich dazu haben StageWise und DataAugment zwar gelernt, bis zu einem gewissen Grad mit gegnerischen Angriffen umzugehen, sie sind jedoch nicht in allen Fällen so effektiv wie ATPA.
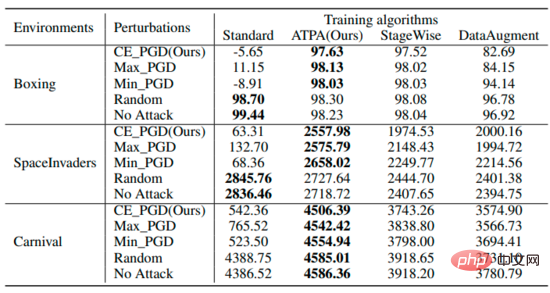
Für einen breiteren Vergleich bewerten die Autoren auch die Robustheit dieser Verteidigungsalgorithmen gegenüber unterschiedlich starken gegnerischen Eingriffen, die von den effektivsten strategischen Angriffsalgorithmen erzeugt werden. Wie unten gezeigt, erhielt ATPA erneut in allen Fällen die höchsten Bewertungen. Darüber hinaus ist die Bewertungsvarianz von ATPA viel geringer als die von StageWise und DataAugment, was darauf hinweist, dass ATPA über eine stärkere generative Fähigkeit verfügt.
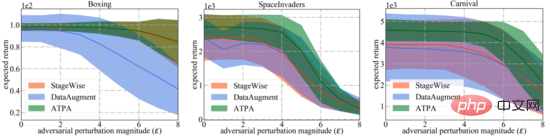
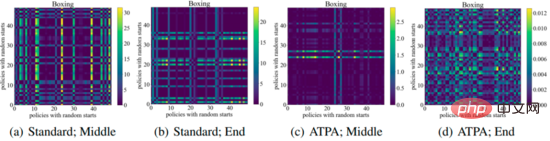
Um eine ähnliche Leistung zu erzielen, benötigt ATPA mehr Trainingsdaten als der Standard-PPO-Algorithmus. Die Autoren gehen dieser Frage nach, indem sie die Stabilität der Störungsstrategie untersuchen. Die Autoren berechneten die KL-Divergenzwerte der Störungsrichtlinie, die durch die Durchführung von Richtlinienangriffen mithilfe von PGD mit unterschiedlichen zufälligen Anfangspunkten in der Mitte und am Ende des Trainingsprozesses erhalten wurden. Wie in der folgenden Abbildung dargestellt, werden ohne kontradiktorisches Training ständig große KL-Divergenzwerte beobachtet, selbst wenn der Standard-PPO konvergiert hat, was darauf hinweist, dass die Richtlinie gegenüber den Störungen, die durch die Durchführung der PGD mit unterschiedlichen Anfangspunkten entstehen, sehr instabil ist.
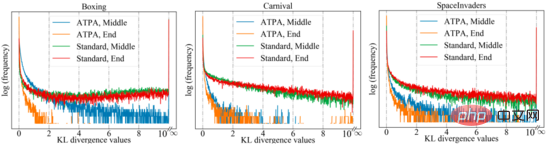
Die folgende Abbildung zeigt das KL-Divergenzdiagramm von Störungsstrategien mit unterschiedlichen Anfangspunkten. Es kann festgestellt werden, dass jedes Pixel in der Abbildung den KL-Divergenzwert zweier Störungsstrategien darstellt. Die Kernformel des Algorithmus ist gegeben. Beachten Sie, dass diese Zuordnungen auch asymmetrisch sind, da es sich bei der KL-Divergenz um eine asymmetrische Metrik handelt.
Das obige ist der detaillierte Inhalt vonGegnerische Angriffe und Abwehrmaßnahmen beim Deep Reinforcement Learning. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 IIS unerwarteter Fehler 0x8ffe2740 Lösung
IIS unerwarteter Fehler 0x8ffe2740 Lösung
 flac-Format
flac-Format
 Welche E-Commerce-Plattformen gibt es?
Welche E-Commerce-Plattformen gibt es?
 Der Unterschied zwischen ++a und a++ in der C-Sprache
Der Unterschied zwischen ++a und a++ in der C-Sprache
 Wo soll ich meinen Geburtsort angeben: Provinz, Stadt oder Kreis?
Wo soll ich meinen Geburtsort angeben: Provinz, Stadt oder Kreis?
 Was ist der Unterschied zwischen 5g und 4g?
Was ist der Unterschied zwischen 5g und 4g?
 So verwenden Sie die magnetische Btbook-Suche
So verwenden Sie die magnetische Btbook-Suche
 So konfigurieren Sie die Pfadumgebungsvariable in Java
So konfigurieren Sie die Pfadumgebungsvariable in Java




