 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Sechs Clustering-Algorithmen, die Datenwissenschaftler kennen müssen
Sechs Clustering-Algorithmen, die Datenwissenschaftler kennen müssen
Sechs Clustering-Algorithmen, die Datenwissenschaftler kennen müssen
Derzeit verwenden viele Anwendungen wie Google News Clustering-Algorithmen als Hauptimplementierungsmethode. Sie können große Mengen unbeschrifteter Daten verwenden, um leistungsstarkes Themen-Clustering zu erstellen. In diesem Artikel werden 6 Arten gängiger Methoden vorgestellt, vom grundlegendsten K-Means-Clustering bis hin zu leistungsstarken dichtebasierten Methoden. Sie haben jeweils ihre eigenen Fachgebiete und Szenarien, und die Grundideen sind nicht unbedingt auf Clustering-Methoden beschränkt.

Dieser Artikel beginnt mit einem einfachen und effizienten K-Means-Clustering und stellt dann Mean-Shift-Clustering, dichtebasiertes Clustering, Clustering mit Gaußschen Mischungs- und Maximum-Erwartungs-Methoden, hierarchisches Clustering und Methoden vor, die für strukturierte Datengruppen geeignet sind Erkennung. Wir analysieren nicht nur die grundlegenden Implementierungskonzepte, sondern geben auch die Vor- und Nachteile jedes Algorithmus an, um tatsächliche Anwendungsszenarien zu verdeutlichen.
Clustering ist eine Technik des maschinellen Lernens, bei der Datenpunkte gruppiert werden. Bei einer gegebenen Menge von Datenpunkten können wir einen Clustering-Algorithmus verwenden, um jeden Datenpunkt einer bestimmten Gruppe zuzuordnen. Theoretisch sollten Datenpunkte, die zur gleichen Gruppe gehören, ähnliche Eigenschaften und/oder Merkmale haben, während Datenpunkte, die zu verschiedenen Gruppen gehören, sehr unterschiedliche Eigenschaften und/oder Merkmale haben sollten. Clustering ist eine unbeaufsichtigte Lernmethode und eine Technik zur statistischen Datenanalyse, die in vielen Bereichen häufig verwendet wird.
K-Means (K-Means) Clustering
K-Means ist wahrscheinlich der bekannteste Clustering-Algorithmus. Es ist Teil vieler Einführungskurse in die Datenwissenschaft und das maschinelle Lernen. Sehr einfach zu verstehen und im Code zu implementieren! Bitte sehen Sie sich das Bild unten an.
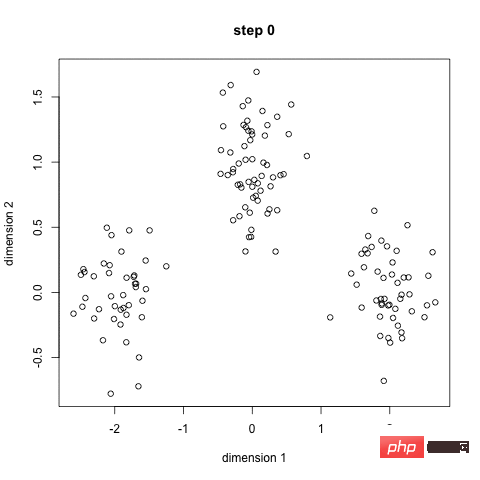
K-Means Clustering
Zuerst wählen wir einige Klassen/Gruppen aus und initialisieren ihre jeweiligen Mittelpunkte zufällig. Um die Anzahl der zu verwendenden Klassen zu ermitteln, empfiehlt es sich, einen kurzen Blick auf die Daten zu werfen und zu versuchen, die verschiedenen Gruppen zu identifizieren. Der Mittelpunkt ist der Ort mit der gleichen Länge wie jeder Datenpunktvektor, der im obigen Bild „X“ ist.
Klassifizieren Sie jeden Punkt, indem Sie den Abstand zwischen dem Datenpunkt und der Mitte jeder Gruppe berechnen, und klassifizieren Sie dann den Punkt in die Gruppe, der die Gruppenmitte am nächsten liegt.
Basierend auf diesen Klassifizierungspunkten verwenden wir den Mittelwert aller Vektoren in der Gruppe, um das Gruppenzentrum neu zu berechnen.
Wiederholen Sie diese Schritte für eine bestimmte Anzahl von Iterationen oder bis sich das Gruppenzentrum nach jeder Iteration kaum ändert. Sie können das Gruppenzentrum auch einige Male nach dem Zufallsprinzip initialisieren und dann den Lauf auswählen, der die besten Ergebnisse zu liefern scheint.
K-Means hat den Vorteil, dass es schnell ist, da wir eigentlich nur den Abstand zwischen dem Punkt und dem Mittelpunkt der Gruppe berechnen: sehr wenig Rechenaufwand! Es hat also eine lineare Komplexität O(n).
Andererseits hat K-Means einige Nachteile. Zuerst müssen Sie auswählen, wie viele Gruppen/Klassen es gibt. Dies geschieht nicht immer sorgfältig, und im Idealfall möchten wir, dass der Clustering-Algorithmus uns bei der Lösung des Problems hilft, wie viele Klassen zu klassifizieren sind, da sein Zweck darin besteht, Erkenntnisse aus den Daten zu gewinnen. K-Means startet auch von zufällig ausgewählten Clusterzentren, sodass es in verschiedenen Algorithmen zu unterschiedlichen Clustering-Ergebnissen führen kann. Daher sind die Ergebnisse möglicherweise nicht reproduzierbar und nicht konsistent. Andere Clustering-Methoden sind konsistenter.
K-Medians ist ein weiterer Clustering-Algorithmus im Zusammenhang mit K-Means, mit der Ausnahme, dass die Gruppenzentren nicht anhand des Mittelwerts, sondern mithilfe des Medianvektors der Gruppe neu berechnet werden. Diese Methode ist unempfindlich gegenüber Ausreißern (da der Median verwendet wird), ist jedoch bei größeren Datensätzen viel langsamer, da bei der Berechnung des Medianvektors bei jeder Iteration eine Sortierung erforderlich ist.
Mean Shift Clustering
Mean Shift Clustering ist ein auf Schiebefenstern basierender Algorithmus, der versucht, dichte Bereiche von Datenpunkten zu finden. Hierbei handelt es sich um einen Schwerpunkt-basierten Algorithmus, dessen Ziel es ist, den Mittelpunkt jeder Gruppe/Klasse zu lokalisieren. Dies wird erreicht, indem die Kandidatenpunkte des Mittelpunkts auf den Mittelwert der Punkte innerhalb des Schiebefensters aktualisiert werden. Diese Kandidatenfenster werden dann in einer Nachbearbeitungsphase gefiltert, um Beinahe-Duplikate zu eliminieren und so den endgültigen Satz von Mittelpunkten und ihren entsprechenden Gruppen zu bilden. Bitte beachten Sie die Legende unten.

Mean-Shift-Clustering für ein einzelnes Schiebefenster
- Um die mittlere Verschiebung zu erklären, betrachten wir eine Menge von Punkten in einem zweidimensionalen Raum, wie in der Abbildung oben gezeigt. Wir beginnen mit einem kreisförmigen Schiebefenster mit Mittelpunkt am Punkt C (zufällig ausgewählt) und einem Kern mit dem Radius r. Die mittlere Verschiebung ist ein Bergsteigeralgorithmus, bei dem bei jedem Schritt bis zur Konvergenz iterativ auf Regionen mit höherer Dichte zugegriffen wird.
- In jeder Iteration bewegt sich das Schiebefenster zu Bereichen mit höherer Dichte, indem der Mittelpunkt in Richtung des Mittelwerts der Punkte innerhalb des Fensters verschoben wird (daher der Name). Die Dichte innerhalb eines Schiebefensters ist proportional zur Anzahl der darin enthaltenen Punkte. Durch die Annäherung an den Mittelwert der Punkte innerhalb des Fensters bewegt es sich natürlich allmählich in Richtung Bereiche mit höherer Punktdichte.
- Wir verschieben das Schiebefenster weiterhin entsprechend dem Mittelwert, bis es keine Richtung mehr gibt, die mehr Punkte im Kernel aufnehmen kann. Schauen Sie sich das Bild oben an; wir bewegen den Kreis so lange, bis die Dichte (d. h. die Anzahl der Punkte im Fenster) nicht mehr zunimmt.
- Der Prozess der Schritte 1 bis 3 wird über viele Schiebefenster durchlaufen, bis sich alle Punkte in einem Fenster befinden. Wenn sich mehrere Schiebefenster überlappen, wird das Fenster mit den meisten Punkten beibehalten. Anschließend wird das Clustering basierend auf dem Schiebefenster durchgeführt, in dem sich die Datenpunkte befinden.
Der gesamte Prozess von Anfang bis Ende für alle Schiebefenster ist unten dargestellt. Jeder schwarze Punkt repräsentiert den Schwerpunkt des Schiebefensters und jeder graue Punkt repräsentiert einen Datenpunkt.

Der gesamte Prozess des Mean-Shift-Clusterings
Im Vergleich zum K-Means-Clustering erfordert diese Methode nicht die Auswahl der Anzahl der Cluster, da die Mean-Shift dies automatisch erkennt. Das ist ein großer Vorteil. Die Tatsache, dass sich die Clusterzentren in Richtung der maximalen Punktdichte gruppieren, ist ebenfalls sehr zufriedenstellend, da es sehr intuitiv ist, die natürlichen datengesteuerten Implikationen zu verstehen und sich daran anzupassen. Der Nachteil besteht darin, dass die Wahl der Fenstergröße/des Fensterradius „r“ möglicherweise unwichtig ist.
Density-Based Clustering Method (DBSCAN)
DBSCAN ist ein dichtebasierter Clustering-Algorithmus, der dem Mean Shift ähnelt, aber einige erhebliche Vorteile bietet. Schauen Sie sich unten eine weitere lustige Grafik an und legen Sie los!
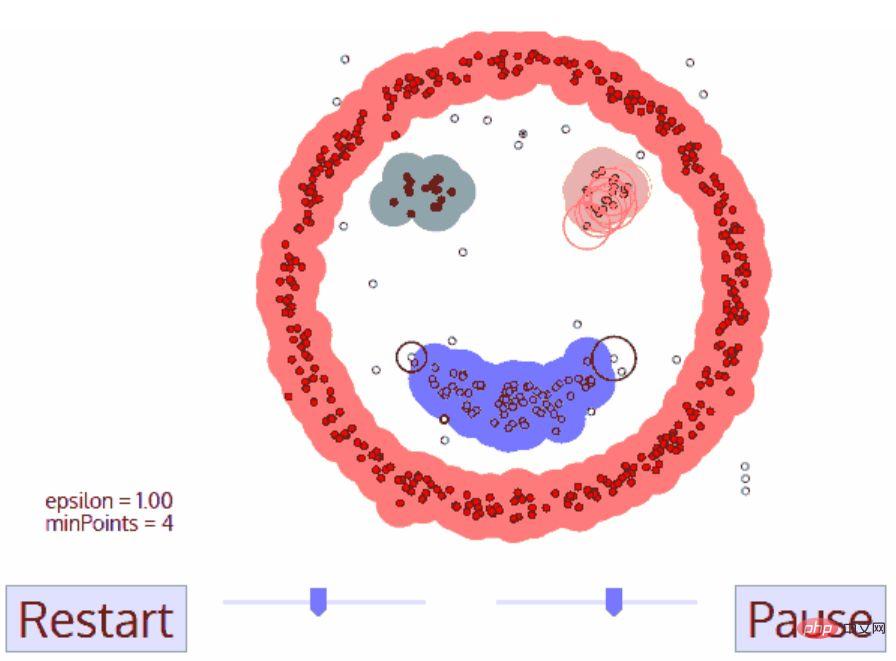
DBSCAN-Clustering
- DBSCAN startet von einem beliebigen Startdatenpunkt, der noch nicht besucht wurde. Die Umgebung dieses Punktes wird mit der Entfernung ε extrahiert (alle Punkte innerhalb der Entfernung ε sind Nachbarpunkte).
- Wenn in dieser Nachbarschaft genügend Punkte vorhanden sind (gemäß minPoints), startet der Clustering-Prozess und der aktuelle Datenpunkt wird zum ersten Punkt des neuen Clusters. Andernfalls wird der Punkt als Rauschen markiert (später kann dieser Rauschpunkt dennoch Teil des Clusters werden). In beiden Fällen wird der Punkt als „Besucht“ markiert.
- Für den ersten Punkt in einem neuen Cluster werden auch Punkte innerhalb seiner ε-Distanz-Nachbarschaft Teil des Clusters. Dieser Vorgang, bei dem alle Punkte in der ε-Nachbarschaft zum selben Cluster gehören, wird für alle neuen Punkte wiederholt, die gerade zum Cluster hinzugefügt wurden.
- Wiederholen Sie die Schritte 2 und 3, bis alle Punkte im Cluster ermittelt sind, d. h. alle Punkte in der ε-Nachbarschaft des Clusters besucht und markiert wurden.
- Sobald wir mit dem aktuellen Cluster fertig sind, wird ein neuer, nicht besuchter Punkt abgerufen und verarbeitet, was zur Entdeckung eines anderen Clusters oder Rauschens führt. Dieser Vorgang wird wiederholt, bis alle Punkte als besucht markiert sind. Da alle Punkte besucht wurden, gehört jeder Punkt zu einem Cluster oder Rauschen.
DBSCAN hat viele Vorteile gegenüber anderen Clustering-Algorithmen. Erstens ist überhaupt keine feste Anzahl von Clustern erforderlich. Außerdem werden Ausreißer als Rauschen identifiziert, im Gegensatz zur Mittelwertverschiebung, bei der Datenpunkte einfach in Clustern gruppiert werden, selbst wenn sie sehr unterschiedlich sind. Darüber hinaus ist es sehr gut in der Lage, Cluster jeder Größe und Form zu finden.
Der Hauptnachteil von DBSCAN besteht darin, dass es nicht so gut funktioniert wie andere Clustering-Algorithmen, wenn die Dichte der Cluster unterschiedlich ist. Dies liegt daran, dass sich die Einstellungen des Entfernungsschwellenwerts ε und minPoints, die zur Identifizierung von Nachbarschaftspunkten verwendet werden, mit Clustern ändern, wenn sich die Dichte ändert. Dieser Nachteil tritt auch bei sehr hochdimensionalen Daten auf, da der Abstandsschwellenwert ε wiederum schwer abzuschätzen ist.
Expectation Maximum (EM) Clustering mit Gaußschen Mischungsmodellen (GMM)
Ein großer Nachteil von K-Means ist die einfache Verwendung von Cluster-Center-Mitteln. Aus dem Diagramm unten können wir ersehen, warum dies nicht der beste Ansatz ist. Auf der linken Seite können Sie sehr deutlich erkennen, dass es zwei kreisförmige Cluster mit unterschiedlichen Radien gibt, deren Mittelpunkt auf dem gleichen Mittelwert liegt. K-Means kann diese Situation nicht bewältigen, da die Mittelwerte dieser Cluster sehr nahe beieinander liegen. K-Means schlägt auch in Fällen fehl, in denen die Cluster nicht kreisförmig sind, wiederum aufgrund der Verwendung des Mittelwerts als Clusterzentrum.

Zwei Fehlerfälle von K-Means
Gaußsche Mischungsmodelle (GMMs) geben uns mehr Flexibilität als K-Means. Für GMMs gehen wir davon aus, dass die Datenpunkte gaußverteilt sind; dies ist eine weniger restriktive Annahme als die Verwendung des Mittelwerts zur Annahme, dass sie kreisförmig sind. Auf diese Weise haben wir zwei Parameter, um die Form des Clusters zu beschreiben: Mittelwert und Standardabweichung! Am Beispiel von 2D bedeutet dies, dass die Cluster jede Art von elliptischer Form annehmen können (da wir Standardabweichungen sowohl in x- als auch in y-Richtung haben). Daher wird jede Gaußsche Verteilung einem einzelnen Cluster zugeordnet.
Um die Gaußschen Parameter (wie Mittelwert und Standardabweichung) jedes Clusters zu ermitteln, verwenden wir einen Optimierungsalgorithmus namens Expectation Maximum (EM). Schauen Sie sich das Diagramm unten an, das ein Beispiel für eine Gaußsche Anpassung an einen Cluster ist. Anschließend können wir den Prozess des Maximum-Expectation-Clusterings mithilfe von GMMs fortsetzen.
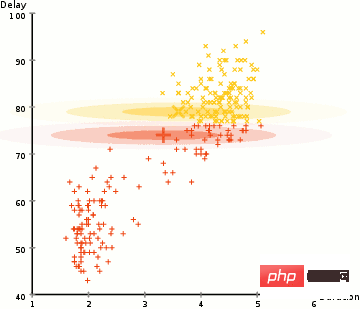
EM-Clustering mit GMMs
- Wir wählen zunächst die Anzahl der Cluster (wie bei K-Means) und initialisieren zufällig die Gaußschen Verteilungsparameter für jeden Cluster. Sie können auch versuchen, durch einen kurzen Blick auf die Daten eine gute Schätzung der Anfangsparameter abzugeben. Beachten Sie jedoch, dass dies, wie Sie oben sehen können, nicht zu 100 % notwendig ist, da die Gaußsche Funktion zunächst sehr schlecht ist, aber schnell optimiert wird.
- Berechnen Sie anhand der Gaußschen Verteilung jedes Clusters die Wahrscheinlichkeit, dass jeder Datenpunkt zu einem bestimmten Cluster gehört. Je näher ein Punkt am Zentrum der Gaußschen Kurve liegt, desto wahrscheinlicher ist es, dass er zu diesem Cluster gehört. Dies sollte intuitiv sein, da wir bei einer Gauß-Verteilung davon ausgehen, dass die meisten Daten näher am Zentrum des Clusters liegen.
- Basierend auf diesen Wahrscheinlichkeiten berechnen wir einen neuen Satz von Gaußschen Verteilungsparametern, die die Wahrscheinlichkeit von Datenpunkten innerhalb des Clusters maximieren. Wir berechnen diese neuen Parameter anhand einer gewichteten Summe der Datenpunktpositionen, wobei das Gewicht die Wahrscheinlichkeit ist, dass der Datenpunkt zu diesem bestimmten Cluster gehört. Um es visuell zu erklären, können wir einen Blick auf das Bild oben werfen, insbesondere auf den gelben Cluster, den wir als Beispiel verwenden. Die Verteilung beginnt sofort bei der ersten Iteration, aber wir können sehen, dass sich die meisten gelben Punkte auf der rechten Seite der Verteilung befinden. Wenn wir eine wahrscheinlichkeitsgewichtete Summe berechnen, liegen einige Punkte zwar in der Nähe der Mitte, aber größtenteils auf der rechten Seite. Daher liegt der Mittelwert der Verteilung natürlich nahe an diesen Punkten. Wir können auch sehen, dass die meisten Punkte „von rechts oben nach links unten“ verteilt sind. Daher wird die Standardabweichung geändert, um eine Ellipse zu erstellen, die besser zu den Punkten passt, um die gewichtete Summe der Wahrscheinlichkeiten zu maximieren.
- Wiederholen Sie die Schritte 2 und 3 bis zur Konvergenz, bei der sich die Verteilung zwischen den Iterationen kaum ändert.
Der Einsatz von GVMs bietet zwei wesentliche Vorteile. Erstens sind GMMs hinsichtlich der Cluster-Kovarianz flexibler als K-Means; aufgrund des Standardabweichungsparameters können Cluster jede elliptische Form annehmen, anstatt auf Kreise beschränkt zu sein. K-Means ist eigentlich ein Sonderfall von GMM, bei dem die Kovarianz jedes Clusters in allen Dimensionen nahe bei 0 liegt. Zweitens kann es viele Cluster pro Datenpunkt geben, da GMMs Wahrscheinlichkeiten verwenden. Wenn sich ein Datenpunkt also in der Mitte zweier überlappender Cluster befindet, können wir seine Klasse einfach dadurch definieren, dass wir sagen, dass X Prozent davon zur Klasse 1 und Y Prozent zur Klasse 2 gehören. Das heißt, GMMs unterstützen hybride Qualifikationen.
Agglomeratives hierarchisches Clustering
Hierarchische Clustering-Algorithmen werden tatsächlich in zwei Kategorien unterteilt: Top-Down oder Bottom-Up. Bottom-up-Algorithmen behandeln zunächst jeden Datenpunkt als einen einzelnen Cluster und führen dann nacheinander zwei Cluster zusammen (oder aggregieren), bis alle Cluster zu einem einzigen Cluster zusammengeführt sind, der alle Datenpunkte enthält. Daher wird hierarchisches Bottom-up-Clustering als agglomeratives hierarchisches Clustering oder HAC bezeichnet. Diese Clusterhierarchie wird durch einen Baum (oder ein Dendrogramm) dargestellt. Die Wurzel des Baumes ist der einzige Cluster, der alle Proben sammelt, und die Blätter sind die Cluster mit nur einer Probe. Bevor Sie mit den Schritten des Algorithmus beginnen, sehen Sie sich bitte die Legende unten an.
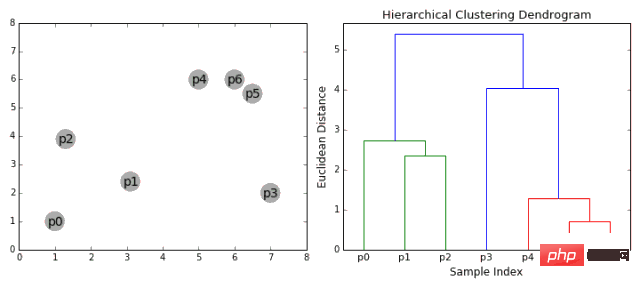
Agglomerative hierarchische Clusterbildung
- Wir behandeln zunächst jeden Datenpunkt als einen einzelnen Cluster, d. h. wenn wir X Datenpunkte in unserem Datensatz haben, dann haben wir X Cluster. Anschließend wählen wir eine Distanzmetrik, die die Distanz zwischen zwei Clustern misst. Als Beispiel verwenden wir die durchschnittliche Verknüpfung, die den Abstand zwischen zwei Clustern als den durchschnittlichen Abstand zwischen Datenpunkten im ersten Cluster und Datenpunkten im zweiten Cluster definiert.
- In jeder Iteration verschmelzen wir zwei Cluster zu einem. Die beiden zusammenzuführenden Cluster sollten die kleinste durchschnittliche Verknüpfung aufweisen. Das heißt, gemäß der von uns gewählten Distanzmetrik haben die beiden Cluster den kleinsten Abstand zwischen sich und sind daher am ähnlichsten und sollten zusammengeführt werden.
- Wiederholen Sie Schritt 2, bis wir die Wurzel des Baums erreichen, d. h. wir haben nur noch einen Cluster, der alle Datenpunkte enthält. Auf diese Weise müssen wir nur entscheiden, wann wir mit dem Zusammenführen von Clustern aufhören möchten, das heißt, wann wir mit dem Aufbau des Baums aufhören möchten, um zu entscheiden, wie viele Cluster wir am Ende benötigen!
Hierarchisches Clustering erfordert nicht, dass wir die Anzahl der Cluster angeben. Wir können sogar auswählen, welche Anzahl von Clustern am besten aussieht, da wir einen Baum erstellen. Darüber hinaus ist der Algorithmus nicht empfindlich gegenüber der Wahl der Distanzmetrik; sie funktionieren alle gleich gut, wohingegen bei anderen Clustering-Algorithmen die Wahl der Distanzmetrik entscheidend ist. Ein besonders gutes Beispiel für hierarchische Clustering-Methoden ist, wenn die zugrunde liegenden Daten eine hierarchische Struktur haben und Sie die Hierarchie wiederherstellen möchten; andere Clustering-Algorithmen können dies nicht. Im Gegensatz zur linearen Komplexität von K-Means und GMM gehen diese Vorteile der hierarchischen Clusterbildung auf Kosten einer geringeren Effizienz, da sie eine zeitliche Komplexität von O(n³) aufweist.
Graph-Community-Erkennung
Wenn unsere Daten als Netzwerk oder Diagramm dargestellt werden können, können wir die Graph-Community-Erkennungsmethode verwenden, um das Clustering abzuschließen. In diesem Algorithmus wird eine Graphengemeinschaft normalerweise als eine Teilmenge von Eckpunkten definiert, die enger miteinander verbunden sind als andere Teile des Netzwerks.
Der vielleicht intuitivste Fall sind soziale Netzwerke. Die Eckpunkte stellen Personen dar, und die die Eckpunkte verbindenden Kanten stellen Benutzer dar, die Freunde oder Fans sind. Um ein System jedoch als Netzwerk zu modellieren, müssen wir einen Weg finden, die verschiedenen Komponenten effizient zu verbinden. Zu den innovativen Anwendungen der Graphentheorie für die Clusterbildung gehören die Merkmalsextraktion von Bilddaten, die Analyse von Genregulationsnetzwerken usw.
Unten sehen Sie ein einfaches Diagramm, das 8 kürzlich aufgerufene Websites zeigt, die über Links auf ihren Wikipedia-Seiten miteinander verbunden sind.
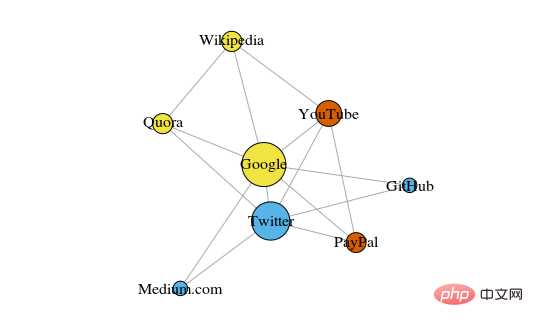
Die Farbe dieser Eckpunkte zeigt ihre Gruppenbeziehung an und die Größe wird anhand ihrer Zentralität bestimmt. Diese Cluster machen auch im wirklichen Leben Sinn, wo die gelben Scheitelpunkte normalerweise Referenz-/Suchseiten und die blauen Scheitelpunkte alle Online-Veröffentlichungsseiten (Artikel, Tweets oder Code) sind.
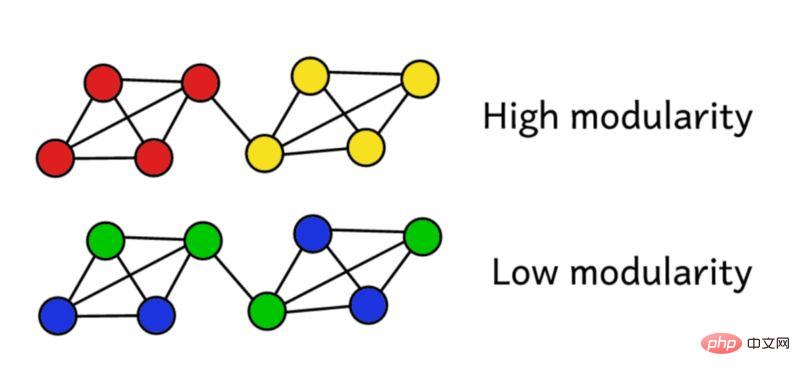
Angenommen, wir haben das Netzwerk in Gruppen gruppiert. Diesen Modularitätswert können wir dann verwenden, um die Qualität des Clusterings zu bewerten. Eine höhere Punktzahl bedeutet, dass wir das Netzwerk in „genaue“ Gruppen segmentiert haben, während eine niedrige Punktzahl bedeutet, dass unsere Clusterbildung eher zufällig ist. Wie in der folgenden Abbildung gezeigt:
Modularität kann mit der folgenden Formel berechnet werden:
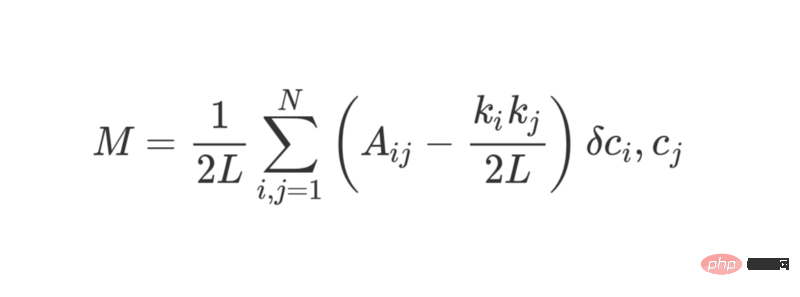
wobei L die Anzahl der Kanten im Netzwerk darstellt, k_i und k_j sich auf den Grad jedes Scheitelpunkts beziehen, der möglich ist berechnet werden, indem jede Zeile addiert wird. Sie wird durch Addition der Elemente in jeder Spalte erhalten. Die Multiplikation der beiden und die Division durch 2L stellt die erwartete Anzahl von Kanten zwischen den Eckpunkten i und j dar, wenn das Netzwerk zufällig zugewiesen wird.
Insgesamt stellen die Begriffe in Klammern den Unterschied zwischen der wahren Struktur des Netzwerks und der erwarteten Struktur dar, wenn sie zufällig kombiniert werden. Die Untersuchung seines Werts zeigt, dass er den höchsten Wert zurückgibt, wenn A_ij = 1 und ( k_i k_j ) / 2L klein ist. Dies bedeutet, dass bei einer „unerwarteten“ Kante zwischen den Fixpunkten i und j der resultierende Wert höher ist.
Das letzte δc_i, c_j ist die berühmte Kronecker-δ-Funktion (Kronecker-Delta-Funktion). Hier ist die Python-Erklärung:

Die Modularität des Diagramms kann mit der obigen Formel berechnet werden. Je höher die Modularität, desto besser ist der Grad der Gruppierung des Netzwerks in verschiedene Gruppen. Der beste Weg, das Netzwerk zu gruppieren, kann daher gefunden werden, indem durch Optimierungsmethoden nach maximaler Modularität gesucht wird.
Kombinatorik sagt uns, dass es für ein Netzwerk mit nur 8 Eckpunkten 4140 verschiedene Clustering-Methoden gibt. Ein Netzwerk aus 16 Eckpunkten würde auf über 10 Milliarden Arten gruppiert werden. Die möglichen Clustering-Methoden eines Netzwerks mit 32 Eckpunkten werden 128 Septillionen (10^21) überschreiten; wenn Ihr Netzwerk 80 Eckpunkte hat, übersteigt die Anzahl der möglichen Clustering-Methoden die Anzahl der Clustering-Methoden im beobachtbaren Universum.
Wir müssen also auf eine Heuristik zurückgreifen, die bei der Bewertung der Cluster mit den höchsten Modularitätswerten gut funktioniert, ohne jede Möglichkeit auszuprobieren. Hierbei handelt es sich um einen Algorithmus namens Fast-Greedy Modularity-Maximization, der dem oben beschriebenen agglomerativen hierarchischen Clustering-Algorithmus etwas ähnelt. Es ist nur so, dass Mod-Max Gruppen nicht basierend auf der Entfernung zusammenfasst, sondern Gruppen basierend auf Änderungen in der Modularität.
So funktioniert es:
- Ordnen Sie zunächst jeden Knoten einer eigenen Gruppe zu und berechnen Sie dann die Modularität M des gesamten Netzwerks.
- Schritt 1 erfordert, dass jedes Community-Paar durch mindestens eine einseitige Verbindung verbunden ist. Wenn zwei Communities zusammengeführt werden, berechnet der Algorithmus die resultierende Modularitätsänderung ΔM.
- Schritt 2 besteht darin, die Gruppenpaare mit dem größten Wachstum in ΔM auszuwählen und sie dann zu fusionieren. Anschließend wird für diesen Cluster eine neue Modularität M berechnet und aufgezeichnet.
- Wiederholen Sie die Schritte 1 und 2 – fusionieren Sie jedes Mal die Gruppenpaare so, dass Sie am Ende den maximalen Gewinn in ΔM erzielen, und zeichnen Sie dann das neue Clustermuster und den entsprechenden Modularitätswert M auf.
- Sie können aufhören, wenn alle Eckpunkte zu einem riesigen Cluster zusammengefasst sind. Der Algorithmus untersucht dann die Datensätze in diesem Prozess und findet das Clustermuster, in dem der höchste M-Wert zurückgegeben wurde. Dies ist die zurückgegebene Gruppenstruktur.
Community-Erkennung ist ein beliebtes Forschungsgebiet in der Graphentheorie. Ihre Einschränkungen spiegeln sich hauptsächlich darin wider, dass sie einige kleine Cluster ignoriert und nur auf strukturierte Graphenmodelle anwendbar ist. Allerdings weist diese Art von Algorithmus eine sehr gute Leistung bei typischen strukturierten Daten und realen Netzwerkdaten auf.
Fazit
Das Obige sind die 6 wichtigsten Clustering-Algorithmen, die Datenwissenschaftler kennen sollten! Am Ende dieses Artikels zeigen wir Visualisierungen verschiedener Algorithmen!
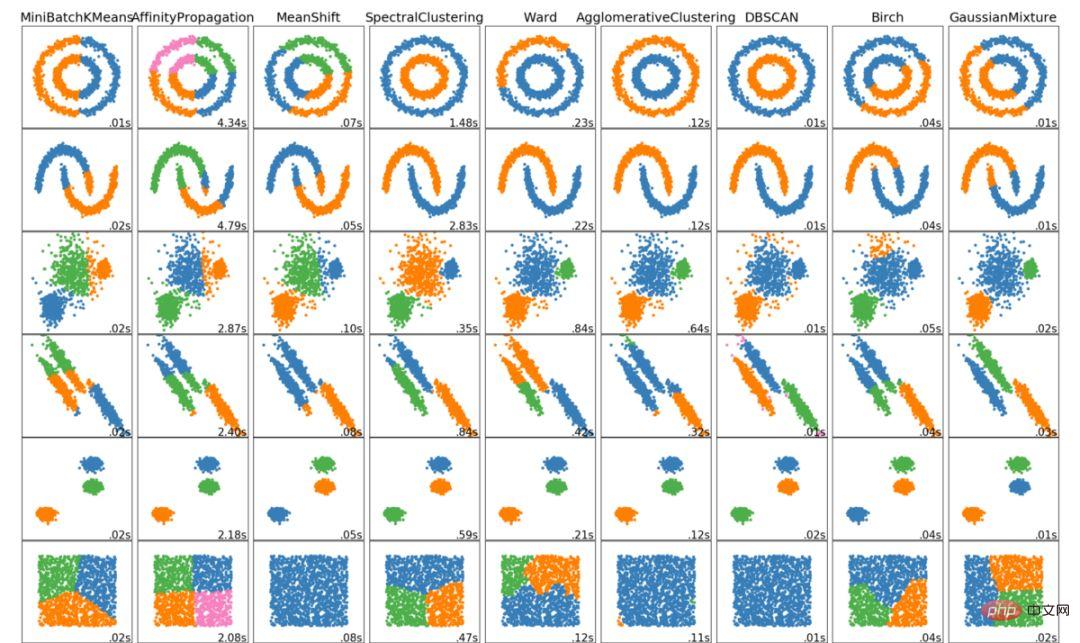
Das obige ist der detaillierte Inhalt vonSechs Clustering-Algorithmen, die Datenwissenschaftler kennen müssen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In den Bereichen maschinelles Lernen und Datenwissenschaft stand die Interpretierbarkeit von Modellen schon immer im Fokus von Forschern und Praktikern. Mit der weit verbreiteten Anwendung komplexer Modelle wie Deep Learning und Ensemble-Methoden ist das Verständnis des Entscheidungsprozesses des Modells besonders wichtig geworden. Explainable AI|XAI trägt dazu bei, Vertrauen in maschinelle Lernmodelle aufzubauen, indem es die Transparenz des Modells erhöht. Eine Verbesserung der Modelltransparenz kann durch Methoden wie den weit verbreiteten Einsatz mehrerer komplexer Modelle sowie der Entscheidungsprozesse zur Erläuterung der Modelle erreicht werden. Zu diesen Methoden gehören die Analyse der Merkmalsbedeutung, die Schätzung des Modellvorhersageintervalls, lokale Interpretierbarkeitsalgorithmen usw. Die Merkmalswichtigkeitsanalyse kann den Entscheidungsprozess des Modells erklären, indem sie den Grad des Einflusses des Modells auf die Eingabemerkmale bewertet. Schätzung des Modellvorhersageintervalls
 Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Zu den häufigsten Herausforderungen, mit denen Algorithmen für maschinelles Lernen in C++ konfrontiert sind, gehören Speicherverwaltung, Multithreading, Leistungsoptimierung und Wartbarkeit. Zu den Lösungen gehören die Verwendung intelligenter Zeiger, moderner Threading-Bibliotheken, SIMD-Anweisungen und Bibliotheken von Drittanbietern sowie die Einhaltung von Codierungsstilrichtlinien und die Verwendung von Automatisierungstools. Praktische Fälle zeigen, wie man die Eigen-Bibliothek nutzt, um lineare Regressionsalgorithmen zu implementieren, den Speicher effektiv zu verwalten und leistungsstarke Matrixoperationen zu nutzen.
 Ist Flash Attention stabil? Meta und Harvard stellten fest, dass die Gewichtsabweichungen ihrer Modelle um Größenordnungen schwankten
May 30, 2024 pm 01:24 PM
Ist Flash Attention stabil? Meta und Harvard stellten fest, dass die Gewichtsabweichungen ihrer Modelle um Größenordnungen schwankten
May 30, 2024 pm 01:24 PM
MetaFAIR hat sich mit Harvard zusammengetan, um einen neuen Forschungsrahmen zur Optimierung der Datenverzerrung bereitzustellen, die bei der Durchführung groß angelegten maschinellen Lernens entsteht. Es ist bekannt, dass das Training großer Sprachmodelle oft Monate dauert und Hunderte oder sogar Tausende von GPUs verwendet. Am Beispiel des Modells LLaMA270B erfordert das Training insgesamt 1.720.320 GPU-Stunden. Das Training großer Modelle stellt aufgrund des Umfangs und der Komplexität dieser Arbeitsbelastungen einzigartige systemische Herausforderungen dar. In letzter Zeit haben viele Institutionen über Instabilität im Trainingsprozess beim Training generativer SOTA-KI-Modelle berichtet. Diese treten normalerweise in Form von Verlustspitzen auf. Beim PaLM-Modell von Google kam es beispielsweise während des Trainingsprozesses zu Instabilitäten. Numerische Voreingenommenheit ist die Hauptursache für diese Trainingsungenauigkeit.
 Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Maschinelles Lernen ist ein wichtiger Zweig der künstlichen Intelligenz, der Computern die Möglichkeit gibt, aus Daten zu lernen und ihre Fähigkeiten zu verbessern, ohne explizit programmiert zu werden. Maschinelles Lernen hat ein breites Anwendungsspektrum in verschiedenen Bereichen, von der Bilderkennung und der Verarbeitung natürlicher Sprache bis hin zu Empfehlungssystemen und Betrugserkennung, und es verändert unsere Lebensweise. Im Bereich des maschinellen Lernens gibt es viele verschiedene Methoden und Theorien, von denen die fünf einflussreichsten Methoden als „Fünf Schulen des maschinellen Lernens“ bezeichnet werden. Die fünf Hauptschulen sind die symbolische Schule, die konnektionistische Schule, die evolutionäre Schule, die Bayes'sche Schule und die Analogieschule. 1. Der Symbolismus, auch Symbolismus genannt, betont die Verwendung von Symbolen zum logischen Denken und zum Ausdruck von Wissen. Diese Denkrichtung glaubt, dass Lernen ein Prozess der umgekehrten Schlussfolgerung durch das Vorhandene ist
 Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Übersetzer |. Rezensiert von Li Rui |. Chonglou Modelle für künstliche Intelligenz (KI) und maschinelles Lernen (ML) werden heutzutage immer komplexer, und die von diesen Modellen erzeugten Ergebnisse sind eine Blackbox, die den Stakeholdern nicht erklärt werden kann. Explainable AI (XAI) zielt darauf ab, dieses Problem zu lösen, indem es Stakeholdern ermöglicht, die Funktionsweise dieser Modelle zu verstehen, sicherzustellen, dass sie verstehen, wie diese Modelle tatsächlich Entscheidungen treffen, und Transparenz in KI-Systemen, Vertrauen und Verantwortlichkeit zur Lösung dieses Problems gewährleistet. In diesem Artikel werden verschiedene Techniken der erklärbaren künstlichen Intelligenz (XAI) untersucht, um ihre zugrunde liegenden Prinzipien zu veranschaulichen. Mehrere Gründe, warum erklärbare KI von entscheidender Bedeutung ist. Vertrauen und Transparenz: Damit KI-Systeme allgemein akzeptiert und vertrauenswürdig sind, müssen Benutzer verstehen, wie Entscheidungen getroffen werden
 Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
01Ausblicksübersicht Derzeit ist es schwierig, ein angemessenes Gleichgewicht zwischen Detektionseffizienz und Detektionsergebnissen zu erreichen. Wir haben einen verbesserten YOLOv5-Algorithmus zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern entwickelt, der mehrschichtige Merkmalspyramiden, Multierkennungskopfstrategien und hybride Aufmerksamkeitsmodule verwendet, um die Wirkung des Zielerkennungsnetzwerks in optischen Fernerkundungsbildern zu verbessern. Laut SIMD-Datensatz ist der mAP des neuen Algorithmus 2,2 % besser als YOLOv5 und 8,48 % besser als YOLOX, wodurch ein besseres Gleichgewicht zwischen Erkennungsergebnissen und Geschwindigkeit erreicht wird. 02 Hintergrund und Motivation Mit der rasanten Entwicklung der Fernerkundungstechnologie wurden hochauflösende optische Fernerkundungsbilder verwendet, um viele Objekte auf der Erdoberfläche zu beschreiben, darunter Flugzeuge, Autos, Gebäude usw. Objekterkennung bei der Interpretation von Fernerkundungsbildern
 Maschinelles Lernen in C++: Ein Leitfaden zur Implementierung gängiger Algorithmen für maschinelles Lernen in C++
Jun 03, 2024 pm 07:33 PM
Maschinelles Lernen in C++: Ein Leitfaden zur Implementierung gängiger Algorithmen für maschinelles Lernen in C++
Jun 03, 2024 pm 07:33 PM
In C++ umfasst die Implementierung von Algorithmen für maschinelles Lernen: Lineare Regression: Wird zur Vorhersage kontinuierlicher Variablen verwendet. Zu den Schritten gehören das Laden von Daten, das Berechnen von Gewichtungen und Verzerrungen, das Aktualisieren von Parametern und die Vorhersage. Logistische Regression: Wird zur Vorhersage diskreter Variablen verwendet. Der Prozess ähnelt der linearen Regression, verwendet jedoch die Sigmoidfunktion zur Vorhersage. Support Vector Machine: Ein leistungsstarker Klassifizierungs- und Regressionsalgorithmus, der die Berechnung von Support-Vektoren und die Vorhersage von Beschriftungen umfasst.
 Anwendung von Algorithmen beim Aufbau einer 58-Porträt-Plattform
May 09, 2024 am 09:01 AM
Anwendung von Algorithmen beim Aufbau einer 58-Porträt-Plattform
May 09, 2024 am 09:01 AM
1. Hintergrund des Baus der 58-Portrait-Plattform Zunächst möchte ich Ihnen den Hintergrund des Baus der 58-Portrait-Plattform mitteilen. 1. Das traditionelle Denken der traditionellen Profiling-Plattform reicht nicht mehr aus. Der Aufbau einer Benutzer-Profiling-Plattform basiert auf Data-Warehouse-Modellierungsfunktionen, um Daten aus mehreren Geschäftsbereichen zu integrieren, um genaue Benutzerporträts zu erstellen Und schließlich muss es über Datenplattformfunktionen verfügen, um Benutzerprofildaten effizient zu speichern, abzufragen und zu teilen sowie Profildienste bereitzustellen. Der Hauptunterschied zwischen einer selbst erstellten Business-Profiling-Plattform und einer Middle-Office-Profiling-Plattform besteht darin, dass die selbst erstellte Profiling-Plattform einen einzelnen Geschäftsbereich bedient und bei Bedarf angepasst werden kann. Die Mid-Office-Plattform bedient mehrere Geschäftsbereiche und ist komplex Modellierung und bietet allgemeinere Funktionen. 2.58 Benutzerporträts vom Hintergrund der Porträtkonstruktion im Mittelbahnsteig 58





