Das kürzlich beliebte Diffusionsmodell, die erste Übersicht über Diffusionserzeugungsmodelle!

Diese Rezension (Diffusion Models: A Comprehensive Survey of Methods and Applications) stammt von Ming-Hsuan Yang von der University of California & Google Research, Cui Bin Laboratory der Peking University und Forschungsteams wie CMU, UCLA, und dem Montreal Mila Research Institute wurde erstmals eine umfassende Zusammenfassung und Analyse der vorhandenen Diffusionsmodelle durchgeführt, beginnend mit der detaillierten Klassifizierung des Diffusionsmodellalgorithmus, seiner Verknüpfung mit anderen fünf großen generativen Modellen und seiner Anwendung in sieben Hauptmodellen Schließlich wurde das Diffusionsmodell vorgeschlagen. Die bestehenden Einschränkungen des Modells und zukünftige Entwicklungsrichtungen.

Artikellink: https://arxiv.org/abs/2209.00796 Diese Überprüfung der Papierklassifizierungszusammenfassung von Diffusionsmodellen Github-Link: https://github.com/YangLing0818/Diffusion-Models-Papers-Survey-Taxonomy

1 Einführung

Diffusionsmodelle sind die neuen SOTA in tiefen generativen Modellen. Das Diffusionsmodell übertrifft das ursprüngliche SOTA: GAN bei Bilderzeugungsaufgaben und weist in vielen Anwendungsbereichen wie Computer Vision, NLP, Wellenformsignalverarbeitung, multimodaler Modellierung, molekularer Graphenmodellierung und Zeitreihenmodellierung eine hervorragende Leistung auf Reinigung usw. Darüber hinaus stehen Diffusionsmodelle in engem Zusammenhang mit anderen Forschungsfeldern wie Robust Learning, Repräsentationslernen und Reinforcement Learning.

Das ursprüngliche Diffusionsmodell weist jedoch auch Mängel auf und erfordert normalerweise Tausende von Bewertungsschritten, um eine Stichprobe zu ziehen. Es ist nicht mit der Wahrscheinlichkeitsschätzung vergleichbar Der Zugriff auf verschiedene Datentypen ist schlecht. Heutzutage haben viele Studien große Anstrengungen unternommen, um die oben genannten Einschränkungen aus der Perspektive praktischer Anwendungen zu lösen, oder die Modellfähigkeiten aus theoretischer Sicht analysiert.

Allerdings mangelt es an einer systematischen Überprüfung der jüngsten Fortschritte bei Diffusionsmodellen von Algorithmen bis hin zu Anwendungen. Um den Fortschritt in diesem schnell wachsenden Bereich widerzuspiegeln, präsentieren wir die erste umfassende Übersicht über Diffusionsmodelle. Wir gehen davon aus, dass unsere Arbeit Licht auf die Designüberlegungen und fortschrittlichen Methoden von Diffusionsmodellen werfen, ihre Anwendungen in verschiedenen Bereichen demonstrieren und zukünftige Forschungsrichtungen aufzeigen wird. Die Zusammenfassung dieser Überprüfung ist in der folgenden Abbildung dargestellt:

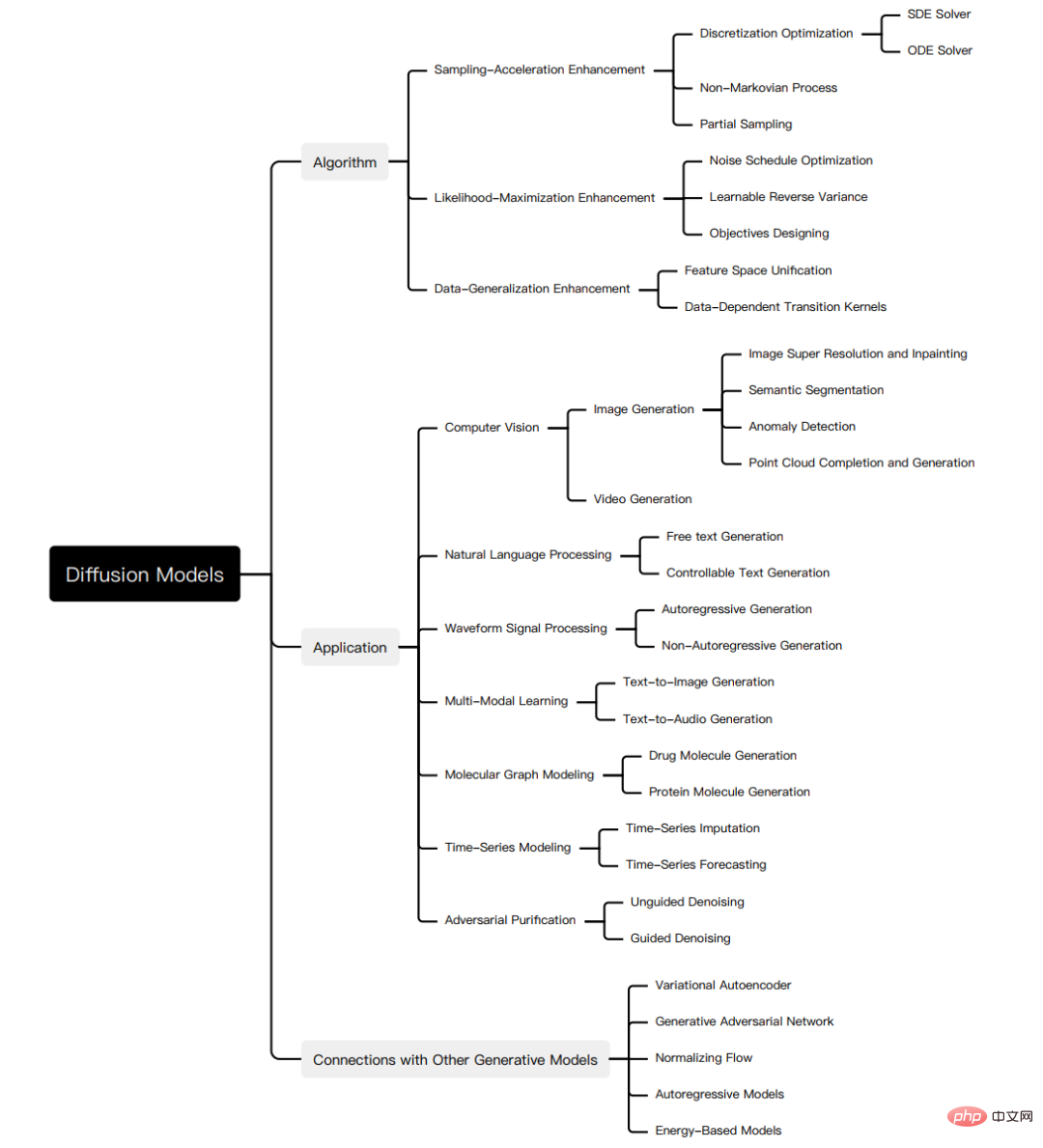
Obwohl das Diffusionsmodell bei verschiedenen Aufgaben eine hervorragende Leistung aufweist, weist es immer noch seine eigenen Mängel auf, und viele Studien haben das Diffusionsmodell verbessert.

Um den Forschungsfortschritt von Diffusionsmodellen systematisch zu klären, haben wir die drei Hauptmängel des ursprünglichen Diffusionsmodells, langsame Abtastgeschwindigkeit, maximale Wahrscheinlichkeitsdifferenz und schwache Fähigkeit zur Datenverallgemeinerung, zusammengefasst und Forschungsarbeiten zur Verbesserung von Diffusionsmodellen vorgeschlagen. Unterteilt in drei entsprechende Kategorien: Verbesserung der Abtastgeschwindigkeit, Verbesserung der maximalen Wahrscheinlichkeit und Verbesserung der Datengeneralisierung.

Wir erläutern zunächst die Motivation zur Verbesserung und klassifizieren dann die Forschung in jeder Verbesserungsrichtung entsprechend den Merkmalen der Methode weiter, um die Zusammenhänge und Unterschiede zwischen den Methoden klar aufzuzeigen. Hier werden nur einige wichtige Methoden als Beispiele ausgewählt, wie in der Abbildung gezeigt:

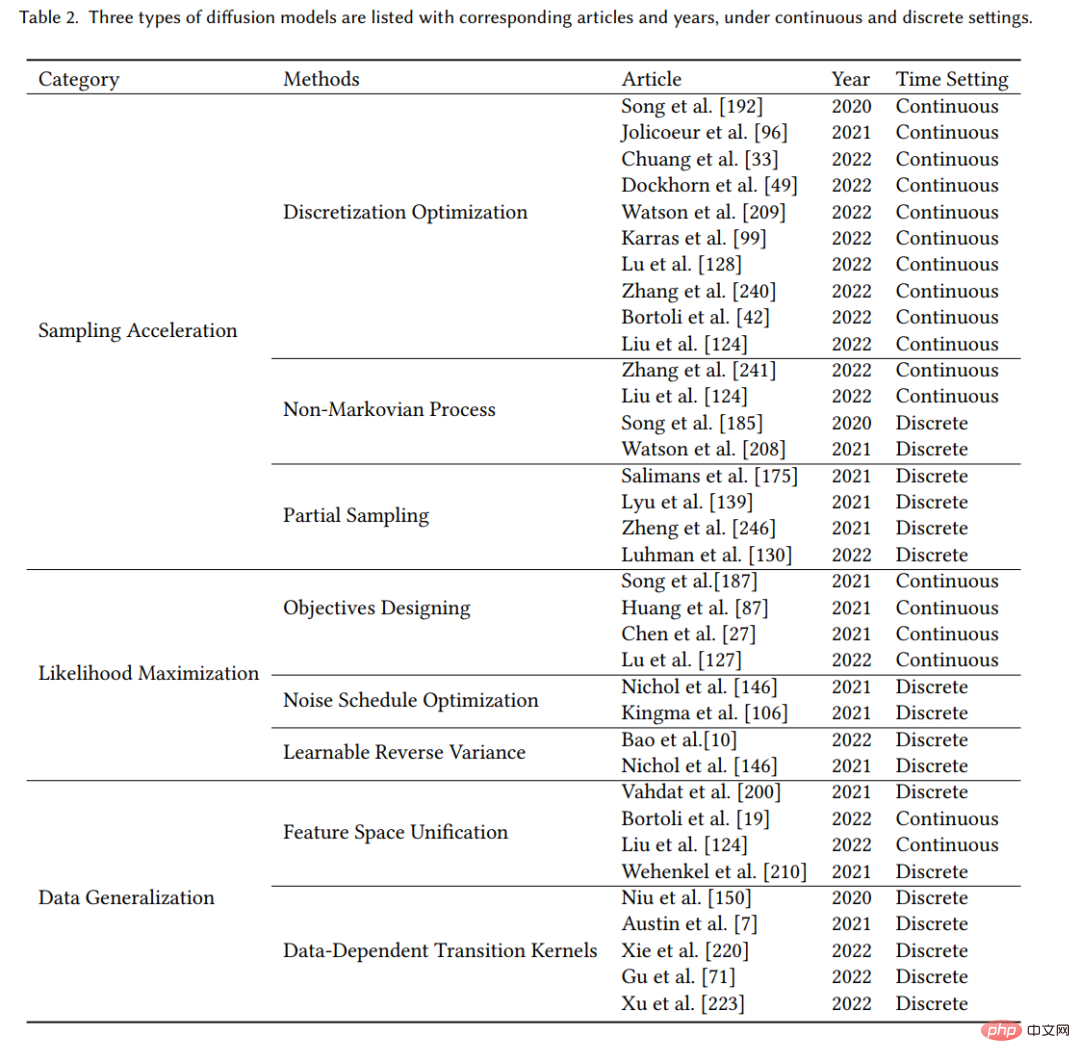
Nach der Analyse der drei Arten von Diffusionsmodellen stellen wir die anderen fünf vor generative Modelle GAN, VAE, autoregressives Modell, normalisierender Fluss und energiebasiertes Modell.

Angesichts der hervorragenden Eigenschaften des Diffusionsmodells haben Forscher das Diffusionsmodell entsprechend seinen Eigenschaften mit anderen generativen Modellen kombiniert. Um die Eigenschaften und Verbesserungsarbeiten des Diffusionsmodells weiter zu demonstrieren, haben wir das Diffusionsmodell eingeführt und andere generative Modelle im Detail Die Modellkombination funktioniert und zeigt Verbesserungen gegenüber dem ursprünglichen generativen Modell.

Das Diffusionsmodell weist in vielen Bereichen eine hervorragende Leistung auf. Angesichts der Tatsache, dass das Diffusionsmodell bei Anwendungen in verschiedenen Bereichen unterschiedliche Verformungen aufweist, haben wir systematisch die Anwendungsforschung des Diffusionsmodells eingeführt, einschließlich der folgenden Bereiche: Computer Vision, NLP, Wellenformsignalverarbeitung , multimodale Modellierung, molekulare Graphenmodellierung, Zeitreihenmodellierung, kontradiktorische Reinigung. Für jede Aufgabe definieren wir die Aufgabe und stellen die Arbeit vor, die das Diffusionsmodell zur Bewältigung der Aufgabe nutzt. Wir fassen die Hauptbeiträge dieser Arbeit wie folgt zusammen:

• Neue Klassifizierungsmethode: Wir schlagen eine neue, systematische Taxonomie von Diffusionsmodellen und ihren Anwendungen vor. Konkret unterteilen wir die Modelle in drei Kategorien: Verbesserung der Abtastgeschwindigkeit, Verbesserung der Maximum-Likelihood-Schätzung und Verbesserung der Datengeneralisierung. Darüber hinaus klassifizieren wir die Anwendungen von Diffusionsmodellen in sieben Kategorien: Computer Vision, NLP, Wellenformsignalverarbeitung, multimodale Modellierung, molekulare Graphenmodellierung, Zeitreihenmodellierung und kontradiktorische Reinigung.
• Umfassender Überblick: Wir bieten den ersten umfassenden Überblick über moderne Diffusionsmodelle und ihre Anwendungen. Wir stellen die wichtigsten Verbesserungen für jedes Diffusionsmodell vor, führen notwendige Vergleiche mit dem Originalmodell durch und fassen die entsprechenden Beiträge zusammen. Für jede Art der Anwendung von Diffusionsmodellen stellen wir die Hauptprobleme vor, mit denen sich Diffusionsmodelle befassen, und erläutern, wie sie diese Probleme lösen.
• Zukünftige Forschungsrichtungen: Wir werfen offene Fragen für zukünftige Forschung auf und geben einige Vorschläge für die zukünftige Entwicklung von Diffusionsmodellen in Bezug auf Algorithmen und Anwendungen.

2 Grundlagen des Diffusionsmodells

Ein Kernproblem bei der generativen Modellierung ist der Kompromiss zwischen Modellflexibilität und Berechenbarkeit. Die Grundidee des Diffusionsmodells besteht darin, die Verteilung in den Daten durch den Vorwärtsdiffusionsprozess systematisch zu stören und dann die Verteilung der Daten durch Erlernen des Rückwärtsdiffusionsprozesses wiederherzustellen, wodurch ein äußerst flexibles und einfach zu berechnendes Modell entsteht generatives Modell. (1) Denoising Diffusion Probabilistic Models (DDPM) Die Funktion der Vorwärtskette besteht darin, die Daten zu stören. Sie fügt den Daten gemäß dem vorgefertigten Rauschplan schrittweise Gaußsches Rauschen hinzu, bis sich die Verteilung der Daten der vorherigen Verteilung, also der Standard-Gaußschen Verteilung, annähert. Die Rückwärtskette beginnt bei einem bestimmten Prior und verwendet einen parametrisierten Gaußschen Transformationskernel, der lernt, die ursprüngliche Datenverteilung schrittweise wiederherzustellen. stellt die Originaldaten und ihre Verteilung dar, dann kann die Verteilung der Vorwärtskette durch die folgende Formel ausgedrückt werden:

Dies zeigt, dass die Vorwärtskette ein Markov-Prozess ist, der nach dem Hinzufügen von t Schritten eine Stichprobe ist Lärm, und es werden im Voraus bestimmte Parameter angegeben, die den Verlauf des Lärms steuern. Wenn sie gegen 1 tendiert, kann davon ausgegangen werden, dass sie der Standard-Gauß-Verteilung entspricht. Wenn er klein ist, kann der Übertragungskern des umgekehrten Prozesses näherungsweise als Gaußscher betrachtet werden:

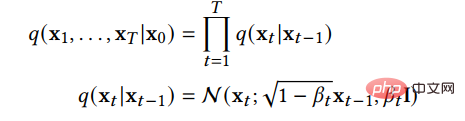Wir können die Variationsuntergrenze als Verlustfunktion lernen:

(2) Punkte- Basierend auf generativen Modellen (SGM)

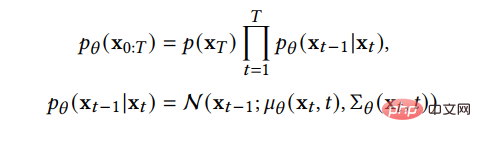
Das obige DDPM kann als diskrete Form von SGM angesehen werden. SGM erstellt eine stochastische Differentialgleichung (SDE), um die Datenverteilung sanft zu stören und die ursprüngliche Datenverteilung in eine bekannte vorherige Verteilung umzuwandeln: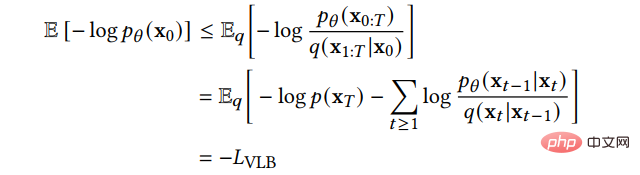

und eine entsprechende inverse SDE, um die vorherige Verteilung zurück in die Rohdatenverteilung umzuwandeln:

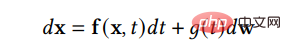Um den Diffusionsprozess umzukehren und Daten zu generieren, benötigen wir also nur die Bruchfunktion zu jedem Zeitpunkt. Mithilfe der Score-Matching-Technik können wir die Score-Funktion durch die folgende Verlustfunktion lernen:

Eine weitere Einführung in die beiden Methoden und die Beziehung zwischen beiden finden Sie in unserem Artikel. Die drei Hauptnachteile des ursprünglichen Diffusionsmodells sind eine langsame Abtastgeschwindigkeit, eine schlechte Wahrscheinlichkeitsmaximierung und eine schwache Fähigkeit zur Datenverallgemeinerung. Viele neuere Studien haben sich mit diesen Mängeln befasst, daher klassifizieren wir verbesserte Diffusionsmodelle in drei Kategorien: Verbesserung der Abtastgeschwindigkeit, Verbesserung der maximalen Wahrscheinlichkeit und Verbesserung der Datenverallgemeinerung. In den nächsten drei, vier und fünf Abschnitten werden wir diese drei Modelltypen im Detail vorstellen.

3 Probenbeschleunigungsmethode

Um die Qualität der neuen Probe zu optimieren, erfordert das Diffusionsmodell bei seiner Anwendung oft Tausende von Berechnungsschritten, um eine neue Probe zu erhalten. Dies schränkt den praktischen Anwendungswert des Diffusionsmodells ein, da wir in der tatsächlichen Anwendung häufig eine große Anzahl neuer Proben generieren müssen, um Materialien für den nächsten Verarbeitungsschritt bereitzustellen.

Forscher haben umfangreiche Untersuchungen zur Verbesserung der Abtastgeschwindigkeit des Diffusionsmodells durchgeführt. Wir beschreiben diese Studien im Detail. Wir verfeinern es in drei Methoden: Diskretisierungsoptimierung, Nicht-Markovian-Prozess und Teilabtastung.

(1) Die Diskretisierungsoptimierungsmethode optimiert die Methode zur Lösung von Diffusions-SDE. Da bei der Lösung komplexer SDE in der Realität nur diskrete Lösungen zur Annäherung an die reale Lösung verwendet werden können, versucht diese Art von Methode, die Diskretisierungsmethode von SDE zu optimieren, um die Anzahl diskreter Schritte zu reduzieren und gleichzeitig die Probenqualität sicherzustellen. SGM schlägt eine allgemeine Methode zur Lösung des Rückwärtsprozesses vor, d. h. die gleiche Diskretisierungsmethode wird für den Vorwärts- und Rückwärtsprozess angewendet. Wenn die Diskretisierungsmethode der Vorwärts-SDE gegeben ist:

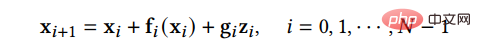
, dann können wir die inverse SDE auf die gleiche Weise diskretisieren:

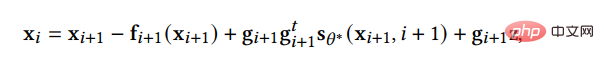
Diese Methode ist etwas besser als das naive DDPM. Darüber hinaus fügt SGM dem SDE-Löser einen Korrektor hinzu, sodass die bei jedem Schritt generierten Stichproben die richtige Verteilung aufweisen. Bei jedem Schritt der Lösung, nachdem dem Löser eine Stichprobe gegeben wurde, verwendet der Geraderichter eine Markov-Ketten-Monte-Carlo-Methode, um die Verteilung der gerade generierten Stichprobe zu glätten. Experimente zeigen, dass das Hinzufügen eines Korrektors zum Löser effizienter ist, als die Anzahl der Schritte im Löser direkt zu erhöhen.

(2) Die Nicht-Markovian-Prozessmethode durchbricht die Einschränkungen des ursprünglichen Markovian-Prozesses. Jeder Schritt des umgekehrten Prozesses kann auf mehr vergangene Proben zurückgreifen, um neue Proben vorherzusagen, sodass dies auch bei der Schrittgröße möglich ist ist groß, um bessere Vorhersagen zu erzielen und dadurch den Stichprobenprozess zu beschleunigen. Unter diesen geht das Hauptwerk DDIM nicht mehr davon aus, dass der Vorwärtsprozess ein Markov-Prozess ist, sondern folgt der folgenden Verteilung:

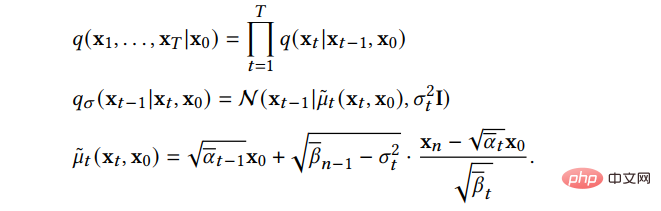
Der Abtastprozess von DDIM kann als diskretisierte göttliche reguläre Differentialgleichung betrachtet werden Der Sampling-Prozess ist effizienter und unterstützt die Sample-Interpolation. Weitere Untersuchungen ergaben, dass DDIM als Sonderfall des On-Manifold-Diffusionsmodells PNDM angesehen werden kann.

(3) Die Partial-Sampling-Methode reduziert direkt die Sampling-Zeit, indem sie einen Teil der Zeitknoten im Generierungsprozess ignoriert und nur die verbleibenden Zeitknoten zum Generieren von Samples verwendet. Beispielsweise destilliert die progressive Destillation ein effizienteres Diffusionsmodell aus einem trainierten Diffusionsmodell. Für ein trainiertes Diffusionsmodell trainiert Progressive Distillation ein Diffusionsmodell neu, sodass ein Schritt des neuen Diffusionsmodells den beiden Schritten des trainierten Diffusionsmodells entspricht, sodass das neue Modell die Hälfte des Probenahmeprozesses des alten Modells einsparen kann. Der spezifische Algorithmus lautet wie folgt:

Durch die kontinuierliche Schleife dieses Destillationsprozesses können die Probenahmeschritte exponentiell reduziert werden.

4 Verbesserung der Maximum-Likelihood-Schätzung

Die Leistung des Diffusionsmodells bei der Maximum-Likelihood-Schätzung ist schlechter als die des generativen Modells basierend auf der Likelihood-Funktion , aber die Maximierung der Wahrscheinlichkeitsschätzung ist in vielen Anwendungsszenarien von großer Bedeutung, wie z. B. Bildkomprimierung, halbüberwachtes Lernen und gegnerische Reinigung. Da es schwierig ist, die Log-Likelihood direkt zu berechnen, konzentriert sich die Forschung hauptsächlich auf die Optimierung und Analyse der Variationsuntergrenzen (VLB). Wir arbeiten an Modellen, die die Maximum-Likelihood-Schätzungen von Diffusionsmodellen verbessern. Wir verfeinern es in drei Kategorien von Methoden: Zielentwurf, Lärmplanungsoptimierung und erlernbare umgekehrte Varianz.

(1) Ziele Die Entwurfsmethode verwendet Diffusions-SDE, um die Beziehung zwischen der Protokollwahrscheinlichkeit der generierten Daten und der Verlustfunktion abzuleiten, die mit der Bewertungsfunktion übereinstimmt. Auf diese Weise können durch geeignete Gestaltung der Verlustfunktion VLB und Log-Likelihood maximiert werden. Song et al. haben bewiesen, dass die Gewichtsfunktion der Verlustfunktion so gestaltet werden kann, dass der Wahrscheinlichkeitsfunktionswert der durch Plug-in-Reverse-SDE erzeugten Stichprobe kleiner oder gleich dem Verlustfunktionswert ist, d. h. die Verlustfunktion die Obergrenze der Wahrscheinlichkeitsfunktion. Die Verlustfunktion für die Teilfunktionsanpassung lautet wie folgt:

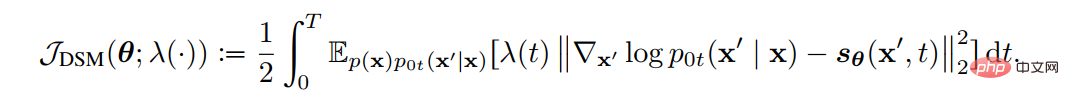
Wir müssen nur die Gewichtsfunktion auf die Diffusion einstellen Der Koeffizient g(t) kann dazu führen, dass die Verlustfunktion zum VLB der Wahrscheinlichkeitsfunktion wird, das heißt: 🎜🎜##🎜🎜 #

(2) Die Optimierung des Geräuschplans erhöht die VLB, indem der Geräuschplan des Vorwärtsprozesses entworfen oder gelernt wird. VDM beweist, dass die Verlustfunktion vollständig durch den Endpunkt der Signal-Rausch-Verhältnis-Funktion SNR(t) bestimmt wird, wenn sich die diskreten Schritte der Unendlichkeit nähern: #

Wenn sich die diskreten Schritte dann der Unendlichkeit nähern, kann VLB optimiert werden Durch Erlernen des Endpunkts der Signal-Rausch-Verhältnis-Funktion SNR(t) können andere Aspekte des Modells durch Erlernen des Funktionswerts des mittleren Teils der Signal-Rausch-Verhältnis-Funktion verbessert werden. 3. Die Methode „Learnable Reverse Variance“ lernt die Varianz des umgekehrten Prozesses, reduziert dadurch Anpassungsfehler und kann VLB effektiv maximieren. Analytic-DPM beweist, dass es im umgekehrten Prozess in DDPM und DDIM einen optimalen Erwartungswert und eine optimale Varianz gibt: Mit der obigen Formel und der trainierten Bruchfunktion kann der optimale VLB unter dem gegebenen Vorwärtsprozess näherungsweise erreicht werden. 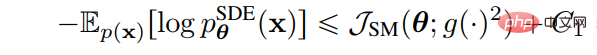5 Verbesserung der Datengeneralisierung

Das Diffusionsmodell geht davon aus, dass die Daten im euklidischen Raum existieren Wenn eine Mannigfaltigkeit mit planarer Geometrie vorhanden ist und Gaußsches Rauschen hinzugefügt wird, werden die Daten unweigerlich in einen kontinuierlichen Zustandsraum umgewandelt, sodass das Diffusionsmodell zunächst nur kontinuierliche Daten wie Bilder verarbeiten kann und weniger effektiv ist, wenn es direkt auf diskrete Daten oder andere Datentypen angewendet wird . Dies schränkt die Anwendungsszenarien des Diffusionsmodells ein.

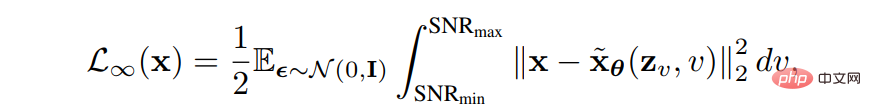Mehrere Forschungsarbeiten verallgemeinern das Diffusionsmodell auf andere Datentypen, und wir erklären diese Methoden im Detail. Wir klassifizieren es in zwei Arten von Methoden: Feature Space Unification und Data-Dependent Transition Kernels.

(1) Die Feature Space Unification-Methode wandelt die Daten in einen einheitlichen latenten Raum um und verteilt sie dann im latenten Raum. LSGM schlägt vor, die Daten über das VAE-Framework in einen kontinuierlichen latenten Raum umzuwandeln und sie dann darauf zu verteilen. Die Schwierigkeit dieser Methode besteht darin, VAE und Diffusionsmodell gleichzeitig zu trainieren. LSGM zeigt, dass der fraktionelle Matching-Verlust nicht mehr gilt, da der zugrunde liegende Prior unlösbar ist. LSGM verwendet direkt die traditionelle Verlustfunktion ELBO in VAE als Verlustfunktion und leitet die Beziehung zwischen ELBO und Score-Matching ab:

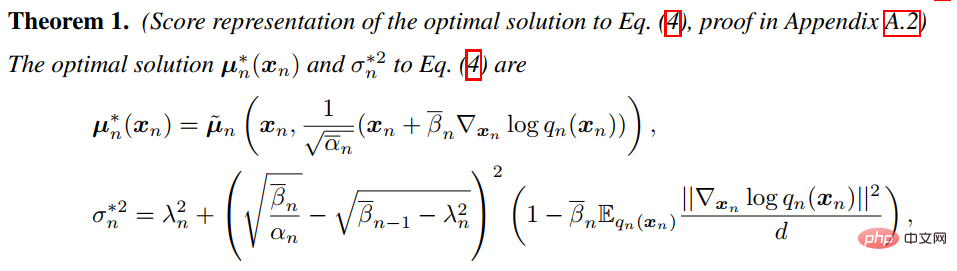
# 🎜 🎜#Diese Formel gilt, wenn Konstanten ignoriert werden. Durch Parametrisieren der Bruchfunktion der Probe im Diffusionsprozess kann LSGM ELBO effizient lernen und optimieren.

(2) Die Methode der datenabhängigen Übergangskerne entwirft die Übergangskerne im Diffusionsprozess entsprechend den Merkmalen des Datentyps, sodass das Diffusionsmodell direkt auf bestimmte Datentypen angewendet werden kann. D3PM hat einen Übergangskernel für diskrete Daten entwickelt, der auf Lazy Random Walk, Absorbing State usw. eingestellt werden kann. GEODIFF entwarf ein translatorisch-rotationsinvariantes graphisches neuronales Netzwerk für 3D-Molekülgraphendaten und bewies, dass die invariante Anfangsverteilung und der Übergangskern eine invariante Randverteilung ableiten können. Angenommen, es handelt sich um eine Translations-Rotations-Transformation, wie zum Beispiel:

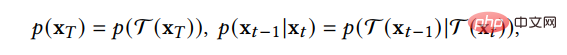
Dann weist die generierte Stichprobenverteilung auch eine Translationsrotation auf Invarianz:

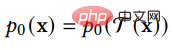
6 Verbinden mit anderen generativen Modellen

#🎜 🎜 #In jedem Unterabschnitt unten stellen wir zunächst die anderen fünf wichtigen Kategorien generativer Modelle vor und analysieren ihre Vorteile und Einschränkungen. Anschließend stellen wir vor, wie Diffusionsmodelle damit zusammenhängen und veranschaulichen, wie diese generativen Modelle durch die Einbeziehung von Diffusionsmodellen verbessert werden können. Die Beziehung zwischen VAE, GAN, autoregressivem Modell, normalisierendem Fluss, energiebasiertem Modell und Diffusionsmodell ist in der folgenden Abbildung dargestellt:

#🎜🎜 ##🎜 🎜#

DDPM kann als hierarchisches Markovian VAE betrachtet werden. Es gibt aber auch Unterschiede zwischen DDPM und allgemeiner VAE. Als VAE gehorchen sowohl der Encoder als auch der Decoder von DDPM der Gaußschen Verteilung und haben die gleiche Dimension wie die Datendimension aller Schichten des Decoders.

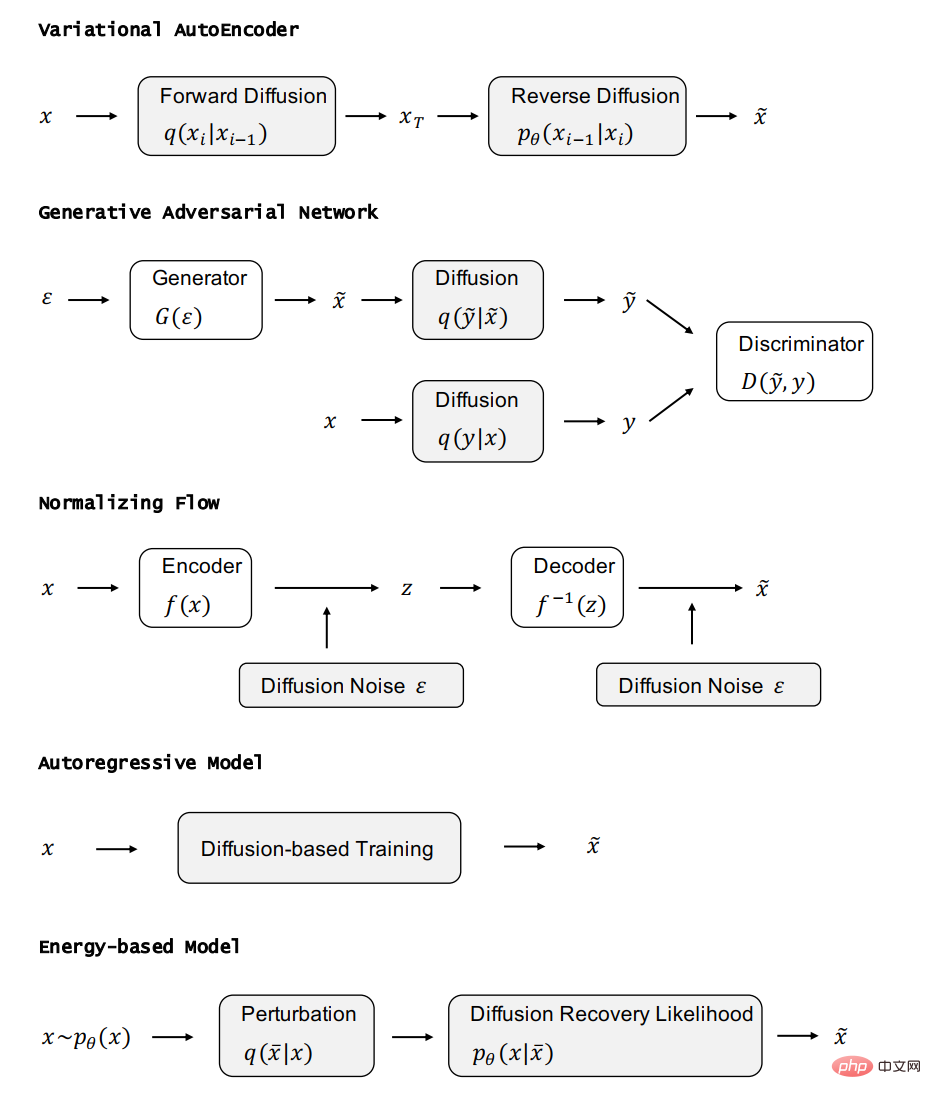• DDPM kann GAN dabei helfen, das Problem des instabilen Trainings zu lösen. Da sich die Daten in einer niedrigdimensionalen Mannigfaltigkeit in einem hochdimensionalen Raum befinden, weist die Verteilung der von GAN generierten Daten eine geringe Überlappung mit der Verteilung der realen Daten auf, was zu einem instabilen Training führt. Das Diffusionsmodell bietet einen Prozess zum systematischen Hinzufügen von Rauschen. Das Diffusionsmodell fügt den generierten Daten und den realen Daten Rauschen hinzu und sendet dann die mit Rauschen versehenen Daten an den Diskriminator. Dadurch kann das Problem, dass GAN nicht trainiert werden kann, effektiv gelöst werden Training ist instabil.
• Normalisierungsfluss wandelt die Daten über eine Bijektionsfunktion in eine vorherige Verteilung um. Dieser Ansatz schränkt die Ausdrucksfähigkeit von Normalisierungsfluss ein, was zu schlechten Anwendungsergebnissen führt. Das analoge Diffusionsmodell fügt dem Encoder Rauschen hinzu, was die Ausdrucksfähigkeit des Normalisierungsflusses erhöhen kann. Aus einer anderen Perspektive besteht dieser Ansatz darin, das Diffusionsmodell auf ein Modell zu erweitern, das auch im Vorwärtsprozess gelernt werden kann.
• Autoregressives Modell muss sicherstellen, dass die Daten eine bestimmte Struktur haben, was es sehr schwierig macht, das autoregressive Modell zu entwerfen und zu parametrisieren. Das Training von Diffusionsmodellen inspirierte das Training autoregressiver Modelle, die durch spezifische Trainingsmethoden Entwurfsschwierigkeiten vermeiden.
• Energiebasiertes Modell modelliert direkt die Verteilung der Originaldaten, aber die direkte Modellierung erschwert das Lernen und die Stichprobenerhebung. Mithilfe der Diffusionswiederherstellungswahrscheinlichkeit kann das Modell der Probe zunächst leichtes Rauschen hinzufügen und dann aus der leicht verrauschten Probenverteilung auf die Verteilung der Originalprobe schließen, wodurch der Lern- und Probenahmeprozess einfacher und stabiler wird.
7

Anwendung des Diffusionsmodells

In diesem Abschnitt stellen wir sie jeweils vor Anwendung des Diffusionsmodells in sieben Hauptanwendungsrichtungen, einschließlich Computer Vision, Verarbeitung natürlicher Sprache, Wellenformsignalverarbeitung, multimodales Lernen, Generierung molekularer Graphen, Zeitreihen und kontradiktorisches Lernen, und die Methoden in jedem Anwendungstyp werden unterteilt und zusammengefasst. Beispielsweise kann in der Bildverarbeitung das Diffusionsmodell zur Bildvervollständigung und -reparatur (RePaint) verwendet werden: Multimodal In der Aufgabe können Sie das Diffusionsmodell verwenden, um Text zu Bild (GLIDE) zu generieren:

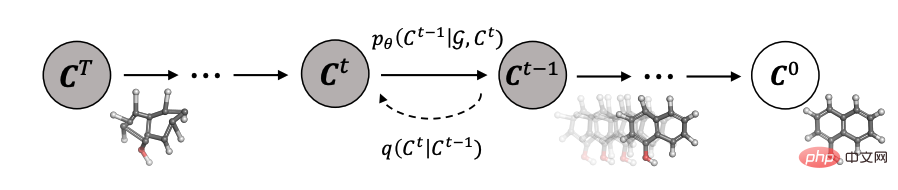
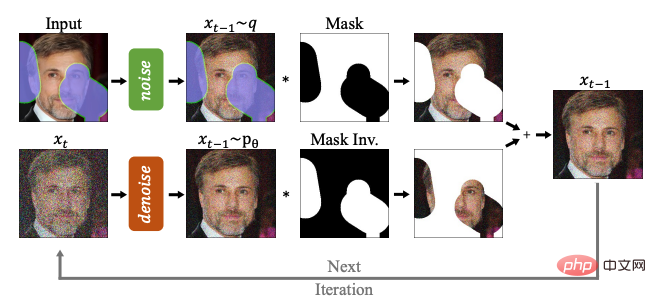kann Kann auch zur Generierung molekularer Diagramme verwendet werden. Verwenden Sie das Diffusionsmodell, um Arzneimittelmoleküle und Proteinmoleküle (GeoDiff) zu generieren:

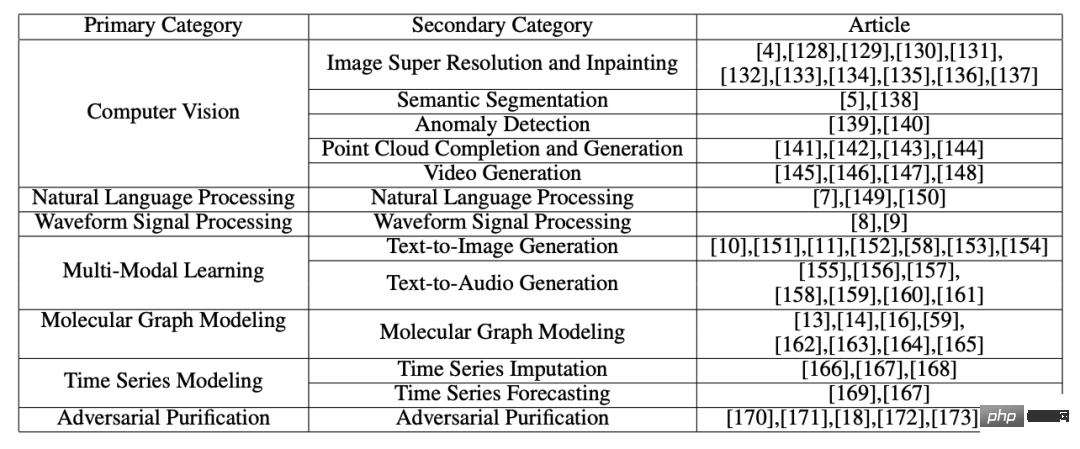
Die Zusammenfassung der Anwendungsklassifizierung wird in der Tabelle angezeigt:

# 🎜🎜#

8 Zukünftige Forschungsrichtung​

#🎜 🎜## 🎜🎜# Wiederholtes Hypothesentesten anwenden. Wir müssen die allgemein akzeptierten Annahmen, die wir in unseren Bewerbungen treffen, prüfen. In der Praxis wird beispielsweise allgemein davon ausgegangen, dass der Vorwärtsprozess des Diffusionsmodells die Daten in eine Standard-Gauß-Verteilung umwandelt. Dies ist jedoch nicht der Fall. Durch weitere Vorwärtsdiffusionsschritte wird die endgültige Stichprobenverteilung näher an die Standard-Gauß-Verteilung herangeführt Verteilung, im Einklang mit dem Stichprobenverfahren, aber mehr Vorwärtsdiffusionsschritte erschweren auch die Schätzung der Bruchfunktion. Theoretische Voraussetzungen sind schwer zu erlangen, was in der Praxis zu einem Missverhältnis zwischen Theorie und Praxis führt. Wir sollten uns dieser Situation bewusst sein und geeignete Diffusionsmodelle entwerfen.

• Von der diskreten Zeit zur kontinuierlichen Zeit. Aufgrund der Flexibilität von Diffusionsmodellen können viele empirische Methoden durch weitere Analysen verbessert werden. Diese Forschungsidee ist vielversprechend, indem sie zeitdiskrete Modelle in entsprechende zeitkontinuierliche Modelle umwandelt und dann mehr und bessere diskrete Methoden entwirft.
• Prozess der neuen Generation. Diffusionsmodelle erzeugen Proben durch zwei Hauptmethoden: Eine besteht darin, die inverse Diffusions-SDE zu diskretisieren und die Proben dann durch die diskretisierte inverse SDE zu erzeugen. Die andere besteht darin, die Markov-Eigenschaften des inversen Prozesses zu verwenden, um die Proben schrittweise zu entrauschen. Für einige Aufgaben ist es jedoch schwierig, diese Methoden zur Generierung von Proben in der Praxis anzuwenden. Daher ist weitere Forschung zu neuen generativen Prozessen und Perspektiven erforderlich.
• Verallgemeinerung auf komplexere Szenarien und mehr Forschungsbereiche. Obwohl das Diffusionsmodell auf viele Szenarien angewendet wurde, sind die meisten davon auf Szenarien mit einer Eingabe und einer Ausgabe beschränkt. In Zukunft können Sie erwägen, es auf komplexere Szenarien wie die Synthese von Text in audiovisueller Sprache anzuwenden. Sie können es auch mit weiteren Forschungsfeldern kombinieren.

Das obige ist der detaillierte Inhalt vonDas kürzlich beliebte Diffusionsmodell, die erste Übersicht über Diffusionserzeugungsmodelle!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!