Menschen müssen viele Wissenspunkte beherrschen, um in verschiedenen Phasen ihres Wachstumsprozesses eine große Anzahl mathematischer Probleme zu lösen. Allerdings bedeutet das Verstehen der Wissenspunkte nicht, dass man sie wirklich versteht. Nur wenn man in der Lage ist, die Probleme zu lösen, kann man menschliche Weisheit widerspiegeln. In den letzten Jahren haben neuronale Netze große Erfolge in den Bereichen Computer Vision, Mustervergleich, Verarbeitung natürlicher Sprache, verstärkendes Lernen usw. erzielt. Allerdings ist die Fähigkeit neuronaler Netze zum Denken über diskrete Kombinationen weitaus geringer als die des Menschen. Können neuronale Netze also mathematische Probleme verstehen und lösen? Wenn ja, wie gut ist die Problemlösungsfähigkeit neuronaler Netze?
In Bezug auf die Datenform kann ein mathematisches Problem als Sequenz betrachtet werden, und seine Lösung (Problemlösungsschritte oder Ausdrücke) wird häufig in Form einer Sequenz dargestellt. Dann kann das Lösen mathematischer Probleme als Übersetzungsproblem von der natürlichen Sprache in die mathematische Sprache betrachtet werden. Das neuronale Netzwerkmodell kann mathematische Probleme formal lösen. Aus verschiedenen früheren Forschungsarbeiten ist bekannt, dass neuronale Netze bei Übersetzungsproblemen eine sehr gute Leistung erzielen können und die menschliche Leistung bei mehreren Datensätzen übertroffen haben. Es unterscheidet sich jedoch erheblich von der maschinellen Übersetzung. Zusätzlich zur Fähigkeit, die Semantik der Frage zu verstehen, erfordert die Lösung mathematischer Probleme häufig die Fähigkeit des Modells, über diskrete Kombinationen algebraischer verallgemeinerter Objekte und Entitäten nachzudenken.
Um die Fähigkeit tiefer Modelle zur Lösung mathematischer Probleme zu erforschen, führte das Human-Machine Intelligence Integration Laboratory der Sun Yat-sen-Universität eine Reihe von Experimenten durch, die auf früheren Forschungsergebnissen basierten und dabei mathematische Anwendungsprobleme und geometrische Berechnungsprobleme in der Grundschule verwendeten und weiterführende Schulen als Ausgangspunkt Forschung verbessert das semantische Verständnis, das kognitive Denken und die mathematischen Problemlösungsfähigkeiten tiefer Modelle. In diesem Artikel wird kurz eine Reihe von Forschungsarbeiten auf dem Gebiet der mathematischen Problemlösung durch das Human-Machine-Object Intelligent Integration Laboratory der Sun Yat-sen-Universität vorgestellt.
Aufsatz 1: Semantisch ausgerichteter universeller Baumstrukturlöser für mathematische Wortprobleme
Die Konferenz 2020 über empirische Methoden in der Verarbeitung natürlicher Sprache
.Papieradresse: https://aclanthology.org/2020.emnlp-main.309.pdf
Ein praktischer Mathe-Wortproblemlöser sollte in der Lage sein, verschiedene Arten von Mathe-Wortproblemen zu lösen, wie zum Beispiel lineare Gleichungen einer Variablen, lineare Gleichungen von zwei Variablengruppen, quadratischen Gleichungen usw. Die meisten Arbeiten zur Lösung mathematischer Anwendungsprobleme sind jedoch nur auf vier arithmetische Operationen ausgelegt, und es ist oft schwierig, diese Art von Entwurf auf weitere Fragetypen zu erweitern. Es ist unmöglich, einen einheitlichen Problemlöser für mathematische Anwendungen zu verwenden, um verschiedene Arten von Ausdrücken gleichzeitig zu lösen gleichzeitig. Bewerbungsfragen. Darüber hinaus fehlen den meisten aktuellen mathematischen Wortproblemlösern semantische Einschränkungen zwischen dem Problemtext und dem Lösungsausdruck.
Als Reaktion auf die oben genannten Probleme schlug das Team des Human-Machine Intelligence Integration Laboratory der Sun Yat-sen University ein einheitliches Ausdrucksbaumdarstellungsschema vor, indem es zusätzliche Operatoren einführte, um mehrere Ausdrücke, eine lineare Gleichung einer Variablen und ein System zu verbinden von linearen Gleichungen zweier Variablen sind, quadratische Gleichungen und andere Arten von Ausdrücken werden auf einheitliche Weise ausgedrückt, was den Entwurf des Lösers vereinfachen und verschiedene Arten von Anwendungsproblemen lösen kann, wie in Abbildung 1 dargestellt. Abbildung 1: Entwurf eines einheitlichen Ausdrucksbaum-Darstellungsschemas in Abbildung 2. Unser baumstrukturierter Universallöser besteht aus zwei Teilen: einem Problem-Encoder, der auf einer zweischichtigen GRU basiert, und einem baumstrukturierten Decoder, der auf einer einheitlichen Ausdrucksbaumdarstellung basiert. Und während des Trainingsprozesses haben wir die Regularisierung der semantischen Ausrichtung eingeführt. Durch die Einschränkung der Konsistenz des Ausdrucksteilbaums und des Fragekontexts kann unser allgemeiner Löser die semantische Beziehung zwischen dem Problem und dem Ausdruck besser berücksichtigen und verschiedene Arten von Problemen untersuchen Wissen, wodurch die Ausdrucksgenerierungsfähigkeiten des Lösers verbessert werden.
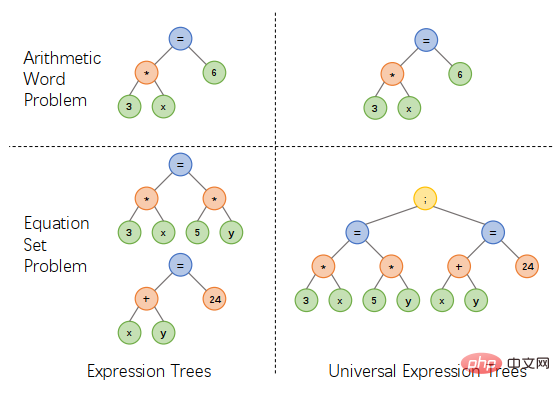
Abbildung 2 Semantischer Ausrichtungsbaumstrukturlöser
Um die Vielseitigkeit und Lösungsfähigkeit des Lösers besser zu messen, haben wir außerdem einen mittelgroßen Datensatz mit mehreren Fragen (HMWP) für Probleme mit einem einzigen Fragentyp im aktuellen Annotationsdatensatz erstellt Beinhaltet das Lösen Tausender mathematischer Textfragen verschiedener Ausdruckstypen, z. B. lineare Gleichungen einer Variablen, lineare Gleichungssysteme zweier Variablen, quadratische Gleichungen einer Variablen usw. Unsere Experimente zeigen, dass Datensätze mit mehreren Fragetypen für Löser eine größere Herausforderung darstellen als Datensätze mit einem einzigen Typ. Sie können auch die Problemlösungsfähigkeit des Lösers besser messen und die Forschung in der Löser-Community fördern.
Im Experiment verglich der Artikel den vorgeschlagenen SAU-Solver mit vorhandenen Methoden in HMWP, Math23K, ALG514 und Dolphin18K-Manual. Die experimentellen Ergebnisse sind in der folgenden Abbildung dargestellt, was die Vielseitigkeit und bessere Fähigkeit unserer Methode zur mathematischen Problemlösung beweist.
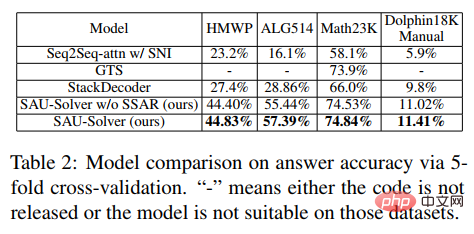
Weitere Forschungsdetails finden Sie im Originalpapier.
Aufsatz 2: Neuronal-symbolischer Löser für mathematische Wortprobleme mit Hilfsaufgaben
Die 59. Jahrestagung der Association for Computational Linguistics und die 11. Internationale gemeinsame Konferenz zur Verarbeitung natürlicher Sprache
Papieradresse: https://arxiv.org/abs/2107.01431
Aktuelle Problemlöser für Elementarmathematik berücksichtigen nicht verschiedene mathematische Symbolbeschränkungen, sondern verwenden einfach Encoder – Probleme mit dem Decoder-Framework, was zu unrealistischen Vorhersagen führt. Die Einführung symbolischer Einschränkungen und symbolischer Argumentation ist für die automatische Lösung mathematischer Anwendungsprobleme von entscheidender Bedeutung.
Daher führte das Team des Human-Machine Intelligence Integration Laboratory der Sun Yat-sen University das neurosymbolische Rechenparadigma ein und schlug einen neuen neurosymbolischen Löser (NS-Solver) vor, um eine explizite Wissensinjektion in Form von Hilfsaufgaben durchzuführen Dadurch werden symbolische Einschränkungen auf verschiedenen Ebenen implementiert. Die technische Architektur ist in Abbildung 3 dargestellt. NS-Solver basiert auf dem Rückgrat des Netzwerks und besteht aus drei Komponenten: 1) Problem Reader, der ein effizientes semantisches Verständnis und die Darstellung mathematischer Probleme durch ein zweischichtiges bidirektionales GRU-Netzwerk durchführt; 2) Programmierer, der für das symbolische Denken verantwortlich ist; Generieren Sie anhand der Problemsemantik und der Vorhersageergebnisse des gesunden Menschenverstandes den Lösungsausdruck. 3) Ausführender, verwenden Sie die Sympy-Bibliothek, um Ausdrücke zu lösen und die endgültige Antwort zu erhalten.
In Bezug auf Symbolbeschränkungen schlagen wir eine Vielzahl von Hilfsaufgaben vor, um zusätzliche Trainingssignale zu nutzen und die Ergebnisse der Vorhersage des gesunden Menschenverstands zu verwenden, um die Symboltabelle explizit einzuschränken und den Suchraum zur Problemlösung zu reduzieren: 1) Selbstüberwachte Ziffernvorhersageaufgabe: durch Sagen Sie die Position und Anzahl der Zahlen in der Frage voraus, um die Semantik der Frage besser zu verstehen. 2) Aufgabe zur Vorhersage des gesunden Menschenverstandes: Fügen Sie gesundes Menschenverstandswissen hinzu und verwenden Sie die Vorhersageergebnisse, um die Symboltabelle einzuschränken, wodurch der Suchraum verringert wird Überprüfen: Überprüfen Sie die Problemlösung auf semantischer Ebene. Die Konsistenz zwischen der Ausgabe des Lösers und dem Zielausdruck. 4) Aufgabe mit doppelter Nutzung: Stärken Sie das semantische Verständnis des Problems durch den Problemlöser durch die bidirektionalen Einschränkungen vom Problem zum Ausdruck und zum Ausdruck zum Problem.
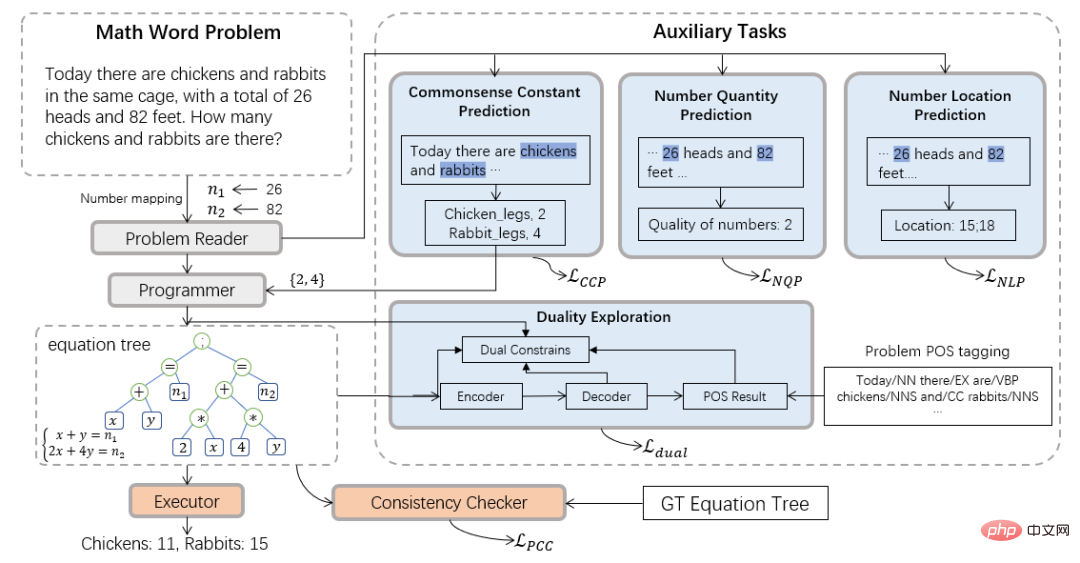
Abbildung 3 Neuronal-Symbolischer Löser (NS-Löser)
Um die Leistung des Lösers besser zu überprüfen, haben wir außerdem ein größeres Multiproblem konstruiert Typ Mathematik-Anwendungsproblemdatensatz CM17K, wodurch die Forschung in der Mathematik-Problemlösungsgemeinschaft besser gefördert wird. CM17K enthält 6215 arithmetische Probleme mit vier Variablen, 5193 lineare Gleichungen einer Variablen, 3129 nichtlineare Gleichungen einer Variablen und 2498 Gleichungsprobleme. Die Datenstatistiken von CM17K und Math23K sind in der folgenden Tabelle aufgeführt. Aus den Statistiken geht hervor, dass CM17K längere Frageninformationen und längere Lösungsausdrücke enthält und mehr gesunden Menschenverstand beinhaltet als Math23K, was bedeutet, dass CM17K die Leistung des Problemlösers in Bezug auf die Lösungsschwierigkeit besser charakterisiert.
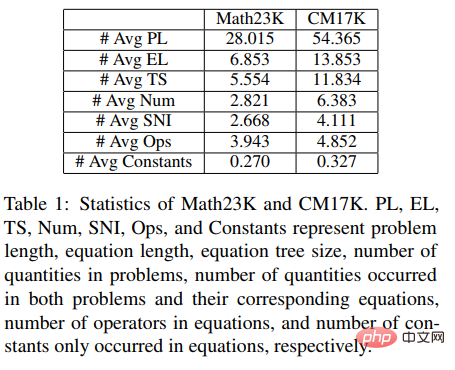
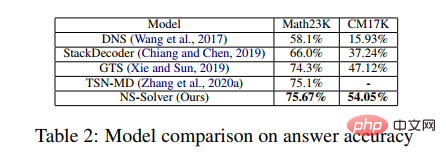
In dem Experiment verglich der Artikel den vorgeschlagenen NS-Solver mit vorhandenen Methoden für Math23K und CM17K und führte Ablationsexperimente durch, die die gute Problemlösungsfähigkeit und Vielseitigkeit von NS-Solver bewiesen. Die Versuchsergebnisse sind in den folgenden beiden Tabellen dargestellt.
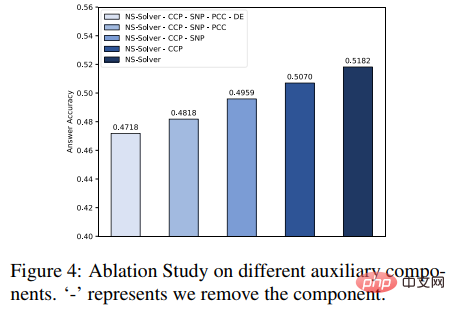
Darüber hinaus haben wir auch Ablationsexperimente zu Hilfsaufgaben durchgeführt, wie in der Abbildung unten dargestellt. Die experimentellen Ergebnisse belegen, dass jede Hilfsaufgabe die Problemlösungsfähigkeit von NS-Solver verbessern kann.
Weitere Forschungsdetails finden Sie im Originalpapier.
Aufsatz 3: GeoQA – Ein geometrischer Frage-Antwort-Benchmark für multimodales numerisches Denken
Ergebnisse der Association for Computational Linguistics: ACL-IJCNLP 2021.
Papieradresse : https://arxiv.org/pdf/2105.14517.pdf
Automatische mathematische Problemlösung hat in letzter Zeit immer mehr Aufmerksamkeit erlangt. Automatisches Lösen mathematischer Probleme Die meisten Arbeiten konzentrieren sich auf das automatische Lösen mathematischer Textprobleme. Allerdings konzentrieren sich nur wenige Arbeiten auf Geometrieprobleme. Im Vergleich zu Mathematikanwendungsfragen erfordern Geometriefragen gleichzeitig das Verständnis von Textbeschreibungen sowie Grafiken und Diagrammen, da sich bei Geometriefragen der Fragetext sowie Grafiken und Diagramme normalerweise ergänzen und unverzichtbar sind. Bestehende Methoden zur automatischen Lösung von Geometrieproblemen sind stark regelabhängig und werden nur an kleinen Datensätzen evaluiert.
... von 5010 Multiple-Choice-Fragen Der Frage-Antwort-Datensatz GeoQA. Wie in Abbildung 4 dargestellt, verfügt jede Probe im GeoQA-Datensatz über eine Fragenbeschreibung, ein geometrisches Bild, Frageoptionen, Antworten, Fragetypen, Wissenspunkte, Lösungsanalyse und formale Verfahren, die durch Problemlösungsschritte gekennzeichnet sind. In Bezug auf die Problemgröße ist dieser Datensatz 25-mal größer als der in früheren Arbeiten häufig verwendete GeoS-Datensatz. Die relevanten statistischen Informationen des GeoQA-Datensatzes sind in der folgenden Tabelle aufgeführt.
Die formalen Programmoperatoren und die beteiligten Konstanten, die vom GeoQA-Datensatz verwendet werden, sind in der folgenden Tabelle aufgeführt.
Um die Forschung zu Geometrieproblemlösern besser zu fördern, haben wir neben der Erstellung einiger Basismodelle auf Basis des GeoQA-Datensatzes auch den Neurogeometrie-Problemlöser NGS vorgeschlagen, um multimodale Semantikinformationen zu verstehen und zu generieren interpretierbare formale Programme. Der Gesamtaufbau des neurogeometrischen Problemlösers NGS ist in Abbildung 5 dargestellt.
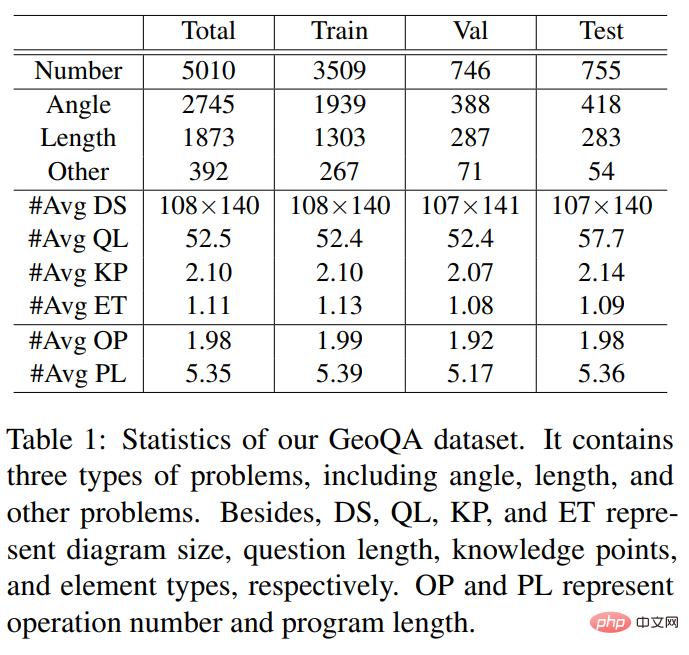
Abbildung 5 Schematische Darstellung des Neurogeometry Problem Solver (NGS) 
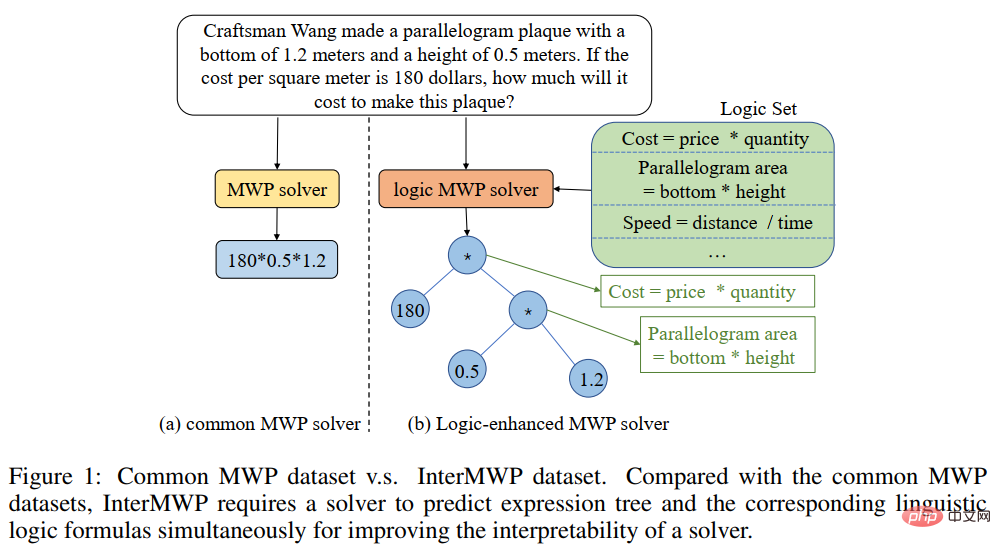
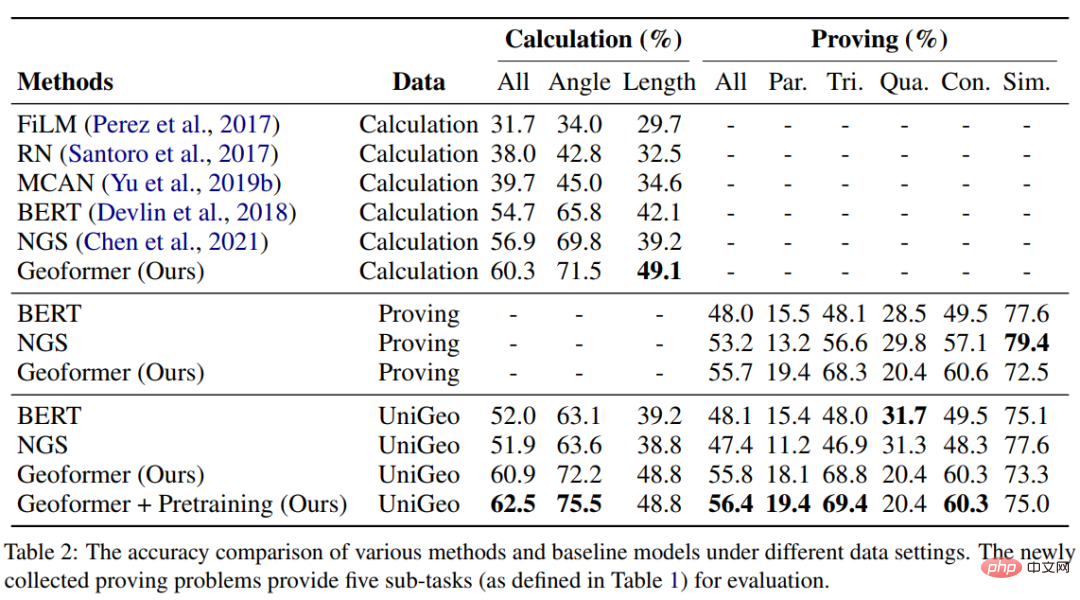
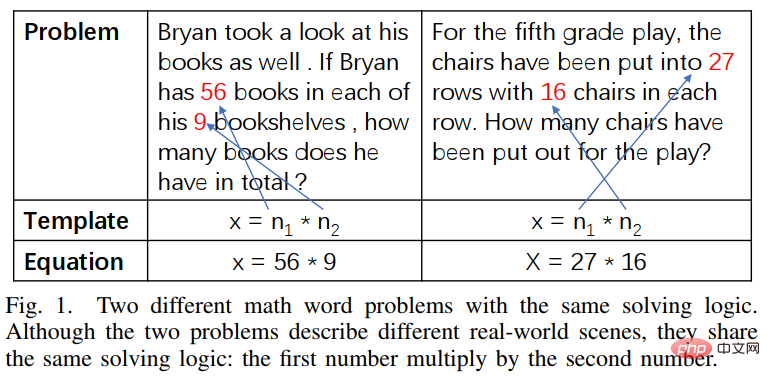
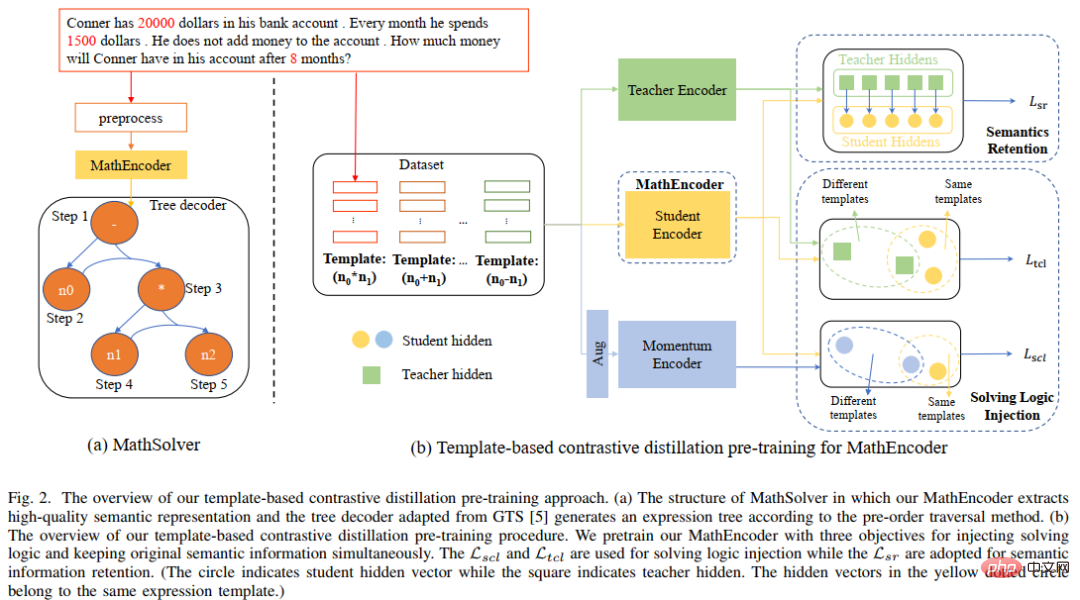
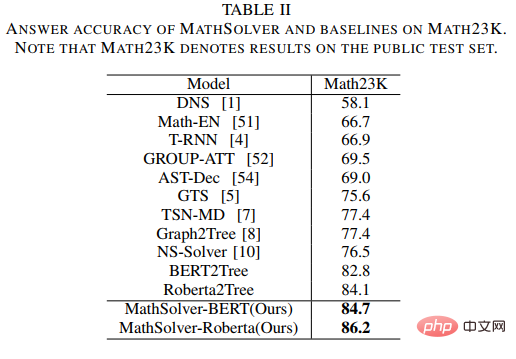
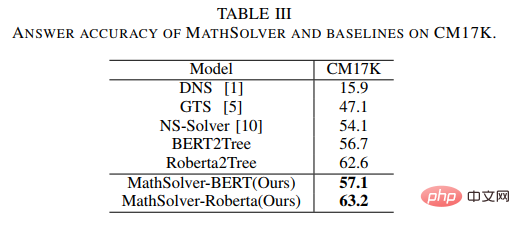
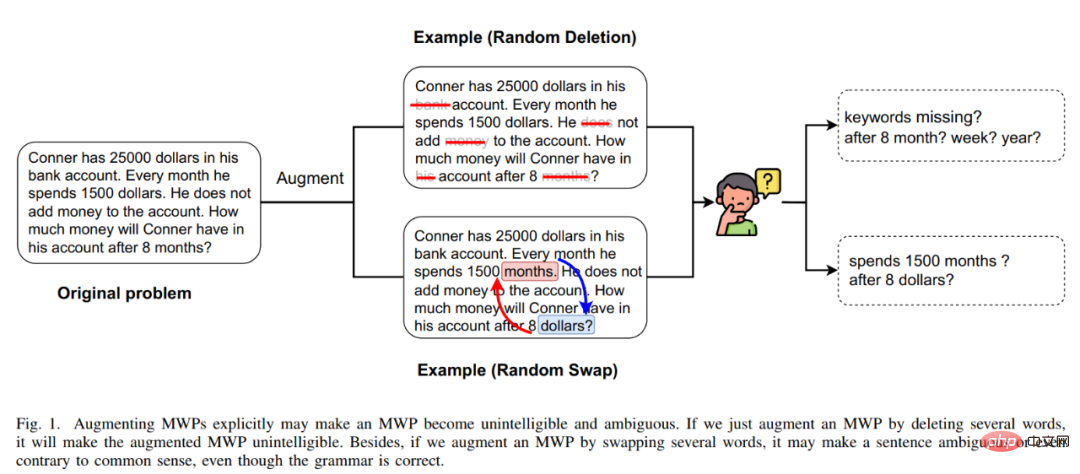
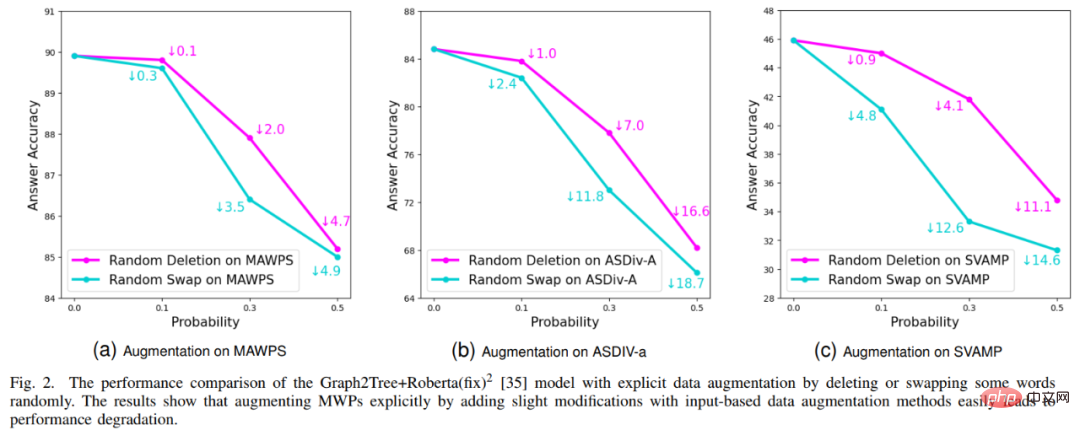
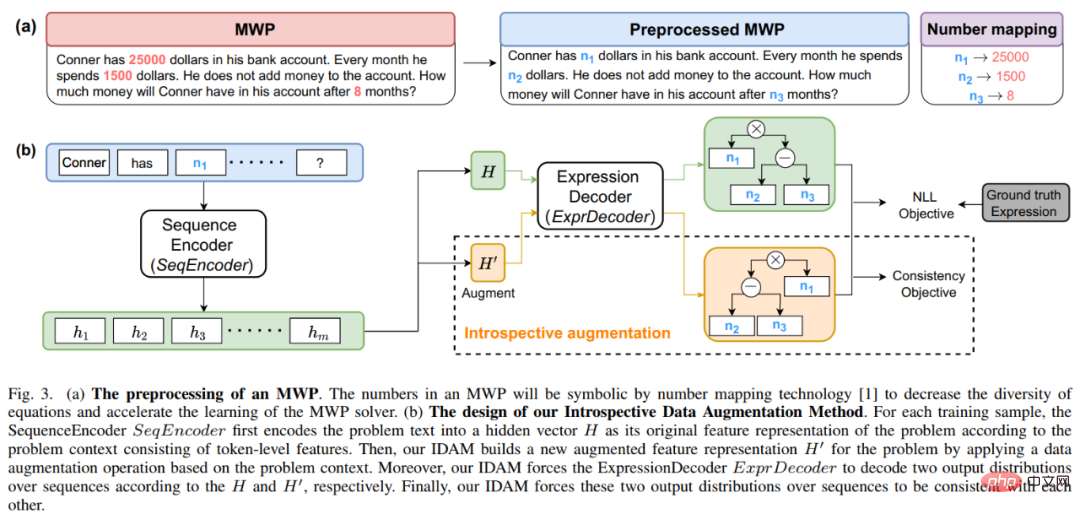
Unser NGS besteht hauptsächlich aus einem Text-Encoder, einem Geometrie-Encoder, einem gemeinsamen Argumentationsmodul und einem Programm-Decoder. Der Text-Encoder ist für die semantische Darstellung des Fragetextes zuständig, der geometrische Figuren-Encoder für die Darstellung geometrischer Figuren. Sowohl die Textdarstellung als auch die grafische Darstellung werden in das gemeinsame Argumentationsmodell für die multimodale semantische Darstellung eingegeben und dem Programmdecoder zur Programmdecodierung zugeführt, und es wird ein interpretierbares und ausführbares formales Lösungsprogramm ausgegeben. Um die Darstellungsfähigkeit geometrischer Figuren durch den Encoder für geometrische Figuren zu verbessern und das gemeinsame Argumentationsmodul zu fördern, um die in der Frage enthaltenen multimodalen Informationen vollständig zu integrieren und effizient auszudrücken, haben wir außerdem eine Vielzahl von eingeführt Hilfsaufgaben zur Verbesserung der Darstellungsfähigkeiten des Modells und zur Einführung von Theoremwissen. Zu diesen Hilfsaufgaben gehören: 1) Puzzle-Positionsvorhersage: Das grafische Verständnis geometrischer Figuren auf Pixelebene wird erreicht, indem die geometrischen Figuren in mehrere Felder geschnitten, zufällig angeordnet werden und sie dann vom Geometrie-Encoder neu angeordnet werden. 2) Geometrische Elemente Vorhersage: Let Der Encoder für geometrische Figuren lernt, vorherzusagen, welche geometrischen Elemente in der aktuellen geometrischen Figur vorkommen, um ein Grafikverständnis auf Objektebene zu erreichen. 3) Wissenspunktvorhersage: Führen Sie eine multimodale Fusion der Fragetextdarstellung und der geometrischen Figurendarstellung im gemeinsamen Argumentationsmodul durch Gleichzeitig wird die Aufgabe der Wissenspunktklassifizierung eingeführt, um die Gesamtproblemdarstellung zu verbessern. In NGS trainieren wir den Geometrie-Encoder vorab mithilfe der Vorhersage der Puzzle-Position und der Vorhersage der Geometrieelemente. Die Wissenspunktvorhersageaufgabe wird als Unteraufgabe für das Multitask-Training mit NGS verwendet. In dem Experiment erstellte der Artikel mehrere auf GeoQA basierende Basismodelle auf Basis neuronaler Netzwerke und verglich NGS mit ihnen. Die experimentellen Ergebnisse von NGS- und Basismodellen für GeoQA sind in der folgenden Tabelle aufgeführt. Wie aus der obigen Tabelle ersichtlich ist, kann NGS bei GeoQA eine bessere Problemlösungsleistung erzielen als das Basismodell. Wir können jedoch auch erkennen, dass bei der Lösung geometrischer Probleme immer noch eine große Lücke zwischen verschiedenen Modellen und Menschen besteht. Darüber hinaus haben wir auch verschiedene Ablationsexperimente durchgeführt, um die Wirksamkeit verschiedener Designs bei NGS zu überprüfen. Weitere Forschungsdetails finden Sie im Originalpapier. 🎞 Papieradresse: https:/ /aclanthology.org/2022.findings-naacl.104.pdf In dieser Arbeit untersucht das Team des Human-Machine Intelligence Integration Laboratory der Sun Yat-sen University die Problemlösungsmethode zur Bewertung des aktuellen Modells erneut Maßstab für die Lösung mathematischer Anwendungsprobleme Bias (Lösungsbias). Diese Problemlösungsverzerrung wird hauptsächlich durch Datenverzerrung und Lernverzerrung verursacht. Datenverzerrung bezieht sich auf das Problem, dass der Trainingsdatensatz nicht alle unterschiedlichen Erzählmethoden jeder Frage abdeckt. Infolgedessen kann das Problemlösungsmodell nur die oberflächliche Semantik erlernen und die tiefe Semantik der Fragebedeutung nicht verstehen Wie in Abbildung 6(a) gezeigt, kann der Problemlöser, selbst nachdem wir den Problemteil des Problems entfernt haben, immer noch 69,4 % erreichen, da das Problemlösungsmodell nur flache Semantik lernt und diese zur Lösung von Problemen verwendet. Die Lernverzerrung bedeutet, dass ein MWP durch mehrere äquivalente Ausdrücke gelöst werden kann, die aktuellen Datensätze jedoch nur eine der äquivalenten Gleichungen als Bezeichnung verwenden, was das Modell dazu zwingt, die Bezeichnung zu lernen und andere äquivalente Gleichungen zu ignorieren, was dazu führt zu einer Voreingenommenheit im Lerntraining. Wie in Abbildung 6(b) dargestellt, generiert das Modell während des Trainingsprozesses möglicherweise einen Ausdruck, der nicht mit dem GroundTruth-Ausdruck übereinstimmt, aber die Antwort ist korrekt. Da der Datensatz jedoch nur einen bestimmten äquivalenten Ausdruck als Bezeichnung verwendet führt dazu: Bei der Berechnung der Verlustfunktion wird der Ausdruck als falscher Ausdruck betrachtet und der Verlust zwischen den beiden korrekten Ausdrücken wird auf das Lösungsmodell zurückpropagiert, was zu einer Überkorrektur des Modells führt. Abbildung 6 Beispiele für Datenverzerrung und Lernverzerrung Um Datenverzerrungen zu mildern, hat das Team des Human-Machine Intelligence Integration Laboratory der Sun Yat-sen University einen neuen Versuch unternommen. Wir haben einen neuen MWP-Benchmark so umbenannt, dass er die Fragen so weit wie möglich abdeckt. Wir haben 2907 Textaufgaben als Basisfragen gesammelt und dann so viele Fragen wie möglich zu den in jeder Frage enthaltenen Geschichten kommentiert. Um den manuellen Anmerkungsprozess zu vereinfachen, generieren wir zunächst einige sinnvolle Ausdrücke basierend auf dem Grundinhalt der Frage und schreiben die Frage dann in umgekehrter Reihenfolge um. Um sinnvolle Ausdrücke zu generieren, haben wir drei Ausdrucksvarianten entworfen: 1) Variablensortiment-Variante (Va): Wählen Sie zufällig zwei numerische Variablen aus dem Grundgerüst der Frage aus und verwenden Sie mathematische Operatoren (+, -, *, /). Kombinieren Sie sie, z als n0 + n1, n0 − n1 usw. 2) Unterausdruckstransformation (Unterausdruck): Alle im Zielausdruck der ursprünglichen Frage enthaltenen Unterausdrücke werden durch Operatoren geändert, wodurch ein neuer Ausdruck erhalten wird. 3) Deformation des gesamten Ausdrucks (Ganze): Erhalten Sie einen neuen Ausdruck, indem Sie die im Zielausdruck der ursprünglichen Frage enthaltenen Operatoren ändern. Die aus den oben genannten drei Varianten erhaltenen neuen Ausdruckssätze werden manuell gefiltert, Ausdrücke, die nicht mit neuen Fragen annotiert werden können, werden herausgefiltert und die verbleibenden Ausdrücke werden manuell mit Fragen annotiert. Um die Lernverzerrung zu mildern, schlagen wir eine dynamische Zielauswahlstrategie vor. Während des Trainingsprozesses wird basierend auf den Ergebnissen der Modellausgabe ein näher daran liegender Zielausdruck als GroundTruth ausgewählt. Um äquivalente Ausdrücke zu erhalten, verwenden wir das Kommutativgesetz in mathematischen Operationen, um den Ausdrucksbaum zu verformen, um mehrere äquivalente Ausdrücke zu erhalten. Wie in Abbildung 7 dargestellt. Abbildung 7 Schematische Darstellung der Generierung äquivalenter Ausdrucksbäume Im Experiment verifizierte der Artikel zunächst den UnbiasedMWP-Datensatz an mehreren SOTA-Basismodellen. Die experimentellen Ergebnisse sind in der folgenden Tabelle aufgeführt. Aus den experimentellen Ergebnissen ist ersichtlich, dass unser Datensatz UnbiasedMWP im Vergleich zum vorhandenen Math23K eine geringere Datenverzerrung aufweist, da die Lösungsleistung des Modells stark abnimmt, wenn wir das Frageproblem entfernen Die Seite, auf der unser Datensatz besser geeignet ist, das Modell zu erstellen, muss auf tiefe semantische Informationen achten, um das Problem zu lösen. Um zu überprüfen, ob unsere dynamische Zielauswahlstrategie Lernverzerrungen reduzieren kann, haben wir die dynamische Zielauswahlstrategie auf mehrere Problemlösungsmodelle angewendet. Die experimentellen Ergebnisse sind in der folgenden Tabelle aufgeführt. Aus den experimentellen Ergebnissen geht hervor, dass unsere dynamische Zielauswahlstrategie die Lernverzerrung wirksam reduzieren und den Lösungseffekt des Modells verbessern kann. Weitere Forschungsdetails finden Sie im Originalpapier. 🔜 Papier Adresse: https://arxiv.org/pdf/2205.08232.pdf Um dieses Problem zu lösen und die Entwicklung des Bereichs der interpretierbaren mathematischen Wortproblemlösung voranzutreiben, hat das Team des Human-Machine Intelligence Integration Laboratory der Sun Yat-sen University den ersten hochwertigen erklärten mathematischen Wortproblemdatensatz InterMWP erstellt. Dieser Datensatz enthält 11.495 mathematische Wortaufgaben und 210 logische Formeln, die auf algebraischem Wissen basieren. Der Lösungsausdruck jeder Wortaufgabe ist mit logischen Formeln versehen. Im Gegensatz zu vorhandenen Datensätzen zur Lösung mathematischer Anwendungsprobleme erfordert unser InterMWP nicht nur, dass der Löser den Lösungsausdruck ausgibt, sondern auch, dass der Problemlöser den logischen Ausdruck basierend auf algebraischem Wissen ausgibt, der dem Lösungsausdruck entspricht, wodurch die Modellerklärung realisiert wird die Ausgabe. Die Ähnlichkeiten und Unterschiede zwischen dem InterMWP-Datensatz und anderen Problemlösungsdatensätzen sind in Abbildung 8 zu sehen. Informationen zum spezifischen Anmerkungsprozess finden Sie im Originaltext. Abbildung 8 Beispiel eines InterMWP-Datensatzes siehe Abbildung 9. Dieses Framework extrahiert relevantes logisches Wissen aus der Bibliothek logischer Formeln als sofortige Informationen durch Abruf, verbessert die semantische Darstellung des MWP durch den Fragen-Encoder und verbessert die Generierungsfähigkeit der logischen Erklärung des MWP. Abbildung 9: LogicSolver-Designdiagramm Logische Wissensabrufkomponente. Für jedes MWP rufen wir die wichtigsten hochrelevanten logischen Formeln aus 210 logischen Formeln als Hinweise zur Verbesserung der MWP-Lösung ab. Wir verbinden logische Formelaufforderungen mit Fragetext als Eingabe, um das MWP-Modell zur Generierung von Lösungsausdrücken anzutreiben. Um schließlich Erklärungen auf der Grundlage logischer Formeln zu erhalten, setzen wir einen Logikgenerator ein, um die logische Formel, die jedem internen Knoten (d. h. Operator) des logischen Ausdrucksbaums entspricht, als Erklärung für die Lösung vorherzusagen. Aus den experimentellen Ergebnissen geht hervor, dass unser LogicSolver in der Antwortgenauigkeit, Formelgenauigkeit und Logikformelgenauigkeit verbessert werden kann, was zeigt, dass unser LogicSolver die Lösungsleistung (Answer Acc und Formula Acc) verbessert mit besserer logischer Interpretierbarkeit (Logic Acc). Weitere Forschungsdetails finden Sie im Originalpapier. Aufsatz 6: UniGeo: Vereinheitlichung des logischen Denkens in der Geometrie durch Neuformulierung mathematischer Ausdrücke Jiaqi Chen, Tong Li, Jinghui Qin, Pan Lu, Liang Lin, Chongyu Chen und Xiaodan Liang Die Konferenz 2022 über empirische Methoden in der Verarbeitung natürlicher Sprache Automatische Geometrieproblemlösung ist ein Maßstab für die Bewertung der multimodalen Argumentationsfähigkeiten tiefer Modelle. In den meisten vorhandenen Arbeiten werden jedoch die automatische Lösung geometrischer Berechnungsprobleme und der automatische Beweis geometrischer Probleme als zwei verschiedene Aufgaben betrachtet, und es werden unterschiedliche Annotationsverarbeitungen angewendet, was die einheitliche Argumentation tiefer Modelle in verschiedenen mathematischen Forschungsfortschritten behindert. Im Wesentlichen haben geometrische Berechnungsfragen und geometrische Beweisfragen ähnliche Problemausdrücke und überschneiden sich in den zu ihrer Lösung erforderlichen mathematischen Kenntnissen. Daher kann die einheitliche Darstellung und das Erlernen der beiden Aufgaben der automatischen Lösung geometrischer Berechnungsprobleme und der automatischen Lösung geometrischer Probleme dazu beitragen, das semantische Verständnis und die symbolische Argumentation tiefer Modelle für diese beiden Probleme zu verbessern. Zu diesem Zweck hat das Team des Human-Machine Intelligence Fusion Laboratory der Sun Yat-sen University einen Benchmark-Datensatz UniGeo erstellt, der Tausende von Geometriefragen enthält. UniGeo umfasst 4.998 geometrische Berechnungsaufgaben und 9.543 geometrische Beweisprobleme. Für jedes Beweisproblem stellen wir mehrstufige Beweisanmerkungen bereit, die problemlos in ausführbare symbolische Programme umgewandelt werden können. Auch die Berechnungsfragen verwenden ähnliche Anmerkungen, wie in Abbildung 10 dargestellt. Nach der Annotation, wie in Abbildung 10 dargestellt, kann UniGeo geometrische Berechnungsprobleme und geometrische Beweisprobleme gut in einer formalen Symbolsprache darstellen. Abbildung 10 UniGeo-Datenbeispiel Nachdem die formale Symbolsprache verwendet wurde, um geometrische Berechnungsfragen und geometrische Beweisfragen einheitlich zu kommentieren, um die einheitliche Darstellungsfähigkeit dieser beiden Fragen effektiv zu überprüfen fördert das semantische Verständnis und die symbolischen Argumentationsfähigkeiten des Modells für geometrische Berechnungsprobleme und geometrische Beweisprobleme und erzielt so effizientere Lösungen für Berechnungsprobleme und Beweisprobleme. Das Team des Human-Machine-Object Intelligent Integration Laboratory der Sun Yat-sen University hat Geoformer für die einheitliche Verarbeitung von geometrischen Problemlösungen und Beweisen entwickelt, um geometrische Berechnungsprobleme und geometrische Beweisprobleme gleichzeitig zu bearbeiten, wie in Abbildung 11 dargestellt. Abbildung 11 GeoFormer-Schema Um einen effizienten Geoformer zu erlernen und ein einheitliches geometrisches Denken zu erreichen, schlug das Team des Human-Machine Intelligence Integration Laboratory der Sun Yat-sen-Universität außerdem weitere Vorschläge vor Mathematische Ausdrucksvorhersage Trainingsaufgaben führen in Kombination mit MLM-Aufgaben ein Aufgabenvortraining auf Geoformer durch, wie in Abbildung 12 dargestellt. Abbildung 12 Schematische Darstellung des Vortrainings für mathematische Ausdrücke Im Experiment haben wir mehrere Basismodelle basierend auf dem UniGeo-Benchmark erstellt und die Leistung unseres vorgeschlagenen GeoFormer verglichen. Die experimentellen Ergebnisse sind in der folgenden Tabelle aufgeführt. Wie aus den experimentellen Ergebnissen hervorgeht, kann der von uns vorgeschlagene GeoFormer sowohl bei Berechnungs- als auch bei Beweisproblem-Unterdatensätzen eine bessere Gesamtleistung als das Basismodell erzielen. Ebenso ist GeoFormer den NGS- und BERT-Basismodellen für den gesamten Datensatz überlegen, der eine einheitliche Lösung von Berechnungs- und Beweisproblemen erfordert. Nach dem Vortraining für mathematische Ausdrücke und dem MLM-Vortraining wird GeoFormer+Pretraining im Vergleich zu GeoFormer weitere Leistungsverbesserungen aufweisen. Diese experimentellen Ergebnisse beweisen vollständig die Wirksamkeit von GeoFormer und veranschaulichen auch, dass einheitliche Modellbegründungen für geometrische Berechnungsprobleme und geometrische Beweisprobleme auch für ihre jeweiligen Aufgaben hilfreich sind. Diese Arbeit wurde in die Hauptkonferenz von EMNLP2022 aufgenommen, bitte bleiben Sie auf dem Laufenden für weitere Forschungsdetails. Papier 7: Vorlagenbasierte kontrastive Destillation Vorschulung für die Lösung mathematischer Wortprobleme Jinghui Qin*, Zhicheng Yang*, Jiaqi Chen, Xiaodan Liang und Liang Lin Obwohl tiefgründig Lernmodelle haben im Bereich der mathematischen Problemlösung gute Fortschritte gemacht, diese Modelle ignorieren jedoch die in der Problembeschreibung enthaltene Lösungslogik, und diese Problemlösungslogik kann häufig der Problemvorlage (Lösung) entsprechen. Wie in Abbildung 13 dargestellt, können zwei verschiedene Textaufgaben jeweils derselben Lösung entsprechen. Abbildung 13 Beispiele für Textaufgaben mit unterschiedlichen Sprachbeschreibungen, aber der gleichen Lösung Darüber hinaus enthalten vorab trainierte Sprachmodelle (PLM) umfangreiches Wissen und verfügen über die Fähigkeit zu einer qualitativ hochwertigen semantischen Darstellung, die bei der Lösung von MWP-Problemen hilfreich sein wird. Um das reichhaltige Wissen des vorab trainierten Sprachmodells voll auszunutzen und Lösungslogik zur effizienteren Lösung von Anwendungsproblemen zu verwenden, schlug das Team des Human-Machine Intelligence Integration Laboratory der Sun Yat-sen University eine vergleichende Destillation vor Basierend auf Lösungsvorlagen und vorab trainierten Sprachmodellen. Die Vortrainingsmethode führt ein Domänenvortraining für den Problemencoder im Löser durch, wie in Abbildung 14 dargestellt. Diese Methode nutzt multiperspektivisches kontrastives Lernen, um mathematisches Logikwissen effektiv zu berücksichtigen, und nutzt gleichzeitig die Wissensdestillation, um das Wissen und die hochwertigen semantischen Darstellungsfähigkeiten im vorab trainierten Sprachmodell effektiv beizubehalten. Konkret verwenden wir zunächst die Konsistenz der Lösungsvorlagen zwischen den beiden Fragen als Zeichen, um zu bestimmen, ob die beiden Fragen im Darstellungsraum nahe beieinander liegen sollten. Anschließend schlagen wir multiperspektivisches vergleichendes Lernen vor, das vergleichendes Lernen von Lehrer-Encodern, Schüler-Encodern und ihren entsprechenden Momentum-Encodern umfasst, sodass zwei Fragedarstellungen mit derselben Lösungsvorlage im Lehrer-Repräsentationsraum und in der Schüler-Repräsentation miteinander interagieren können Raum erreichen, um die Injektion von Lösungslogik zu erreichen. Um das Wissen und die hochwertigen Darstellungsmöglichkeiten des Student-Encoders, der mit einem vorab trainierten Sprachmodell initialisiert wurde, so weit wie möglich beizubehalten, verwenden wir außerdem die Wissensdestillation, um die Darstellung des Student-Encoders mithilfe der Merkmalsdarstellung einzuschränken des Lehrer-Encoders als Aufsicht, um die gleichen Darstellungsfähigkeiten wie der ausgebildete Lehrer-Encoder zu haben und dadurch semantische Erhaltung zu erreichen. Abbildung 14 Vergleichende Destillations-Vortrainingsmethode basierend auf Lösungsvorlage und vorab trainiertem Sprachmodell Im Experiment verwenden wir verschiedene vorab trainierte Sprachmodelle als Initialisierung und überprüfen unsere Methode Wirkung. Wir initialisieren den Problem-Encoder MathEncoder mit BERT-Basis- bzw. Roberta-Basis-Gewichten und verwenden den Decoder in GTS als Ausdrucksdecoder. Wir bezeichnen Solver, die auf MathEncoder basieren, zusammenfassend als MathSolver. Wir haben MathSolver mit mehreren Methoden auf Math23K und CM17K verglichen. Die experimentellen Ergebnisse sind in der folgenden Tabelle aufgeführt. Wie aus den experimentellen Ergebnissen hervorgeht, kann die von uns vorgeschlagene Methode die Problemlösungsfähigkeit des Lösers effektiv verbessern und auf eine Vielzahl verschiedener vorab trainierter Sprachmodelle angewendet werden. Die Ergebnisse wurden an IEEE Transactions on Neural Networks and Learning Systems übermittelt. Weitere Einzelheiten erfahren Sie hier. Aufsatz 8: Eine introspektive Datenerweiterungsmethode zum Trainieren von Problemlösern für mathematische Wörter Jinghui Qin, Zhongzhan Huang, Ying Zeng und Liang Lin In den letzten Jahren haben immer mehr Forscher begann, Methoden zu studieren, die auf Deep Learning basieren, um mathematische Anwendungsprobleme automatisch zu lösen, da die automatische Lösung mathematischer Anwendungsprobleme den Grad der maschinellen Intelligenz vollständig demonstrieren kann. Da die Annotation hochwertiger und umfangreicher MWP-Datensätze sehr kostspielig ist und beispielsweise Fachwissen mit entsprechenden Bildungsniveaus und groß angelegten zugänglichen Fragedaten erfordert, reicht der Umfang der vorhandenen hochwertigen MWP-Datensätze nicht aus, um einen effizienten MWP zu trainieren Lösung. Fragemaschinen reichen nicht aus. Das Datenengpassproblem von MWP ermutigt uns, darüber nachzudenken, wie wir kostengünstige Methoden zur Datenerweiterung nutzen können, um die Effizienz der Datennutzung und die Löserleistung zu verbessern. Die direkteste Datenverbesserungsmethode ist die auf Eingaben basierende Datenverbesserungsmethode, z. B. häufig verwendete Zeichenersetzung, Zeichenlöschung usw. Diese Art von Methode ist jedoch nicht für MWP geeignet, da MWP die Merkmale Prägnanz und Prägnanz aufweist Andernfalls wird der Eingabetext gestört. Oder eine Änderung kann dazu führen, dass die Bedeutung der Frage unklar wird. Darüber hinaus kann die in der Bedeutung der Frage enthaltene mathematische Beziehung nicht geändert werden, aber diese Art von Methode wird wahrscheinlich die in der Bedeutung der Frage enthaltene mathematische Beziehung ändern, wie in Abbildung 15 dargestellt. Abbildung 15 Beispiel für die eingabebasierte Datenverbesserungsmethode, die nicht für MWP-Aufgaben geeignet ist Darüber hinaus führte das Team des Human-Machine-Object Intelligence Fusion Laboratory der Sun Yat-sen University auch Untersuchungen durch Die experimentellen Ergebnisse zur eingabebasierten Datenverbesserungsmethode sind in Abbildung 16 dargestellt. Experimentelle Ergebnisse zeigen, dass die eingabebasierte explizite Datenerweiterungsmethode nicht auf die MWP-Aufgabe anwendbar ist und das bei der MWP-Aufgabe auftretende Datenengpassproblem nicht wirksam lindern kann. Abbildung 16 Die eingabebasierte Datenverbesserungsmethode kann den MWP-Problemlösungseffekt nicht verbessern Aus diesem Grund schlagen wir eine einfache und effiziente Datenverbesserungsmethode vor, die für MWP-Daten geeignet ist – Selbstbeobachtung Die integrierte Datenerweiterungsmethode (IDAM) verbessert die Darstellung der Frage im latenten Raum während des Trainingsprozesses und löst dadurch die Probleme, die bei eingabebasierten Datenerweiterungsmethoden bei MWP-Lösungsaufgaben auftreten. Die IDAM-Methode führt verschiedene Darstellungskonstruktionsmethoden durch (mittleres Pooling, hierarchische Aggregation, zufälliges Verwerfen, zufälliger Austausch usw.), indem sie die Darstellung des Problems codiert, um eine neue Problemdarstellung zu erhalten, und dann die Konsistenzzielfunktion (basierend auf dem Ausdruck) verwendet zwischen JS-Divergenz), um die Ausdrucksdekodierungsausgabe des Lösers basierend auf der neuen Problemdarstellung so einzuschränken, dass sie mit der Ausdrucksdekodierungsausgabe basierend auf der ursprünglichen Problemdarstellung übereinstimmt. Ein schematisches Diagramm der Methode ist in Abbildung 17 dargestellt. Abbildung 17 Schematische Darstellung der introspektiven Datenerweiterungsmethode (IDAM) Im Experiment haben wir IDAM in mehrere SOTA-Methoden eingebettet und sie anhand mehrerer Datensätze verglichen, was die Wirksamkeit bestätigt und Vielseitigkeit unserer IDAM-Methode. Die experimentellen Ergebnisse sind in der folgenden Tabelle aufgeführt. Aus den experimentellen Ergebnissen ist ersichtlich, dass unser IDAM unter derselben experimentellen Konfiguration die Leistung verschiedener Solver-Basismodelle für verschiedene MWP-Datensätze verbessern kann. Dies verdeutlicht vollständig die Wirksamkeit unseres IDAM-Ansatzes für das MWP-Problem. Dieses Ergebnis wurde an IEEE/ACM Transactions on Audio, Speech and Language Processing übermittelt, bitte bleiben Sie auf dem Laufenden, um weitere Einzelheiten zu erfahren. Einführung in das Labor Das Human-Computer Intelligence Convergence Laboratory (HCP Lab) der Sun Yat-sen University wurde 2010 von Professor Lin Li gegründet. Es konzentriert sich auf Forschungsthemen zu modernster Technologie der künstlichen Intelligenz und gewann den ersten Preis für Wissenschaft und Technologie des Chinese Society of Image and Graphics Award, den Wu Wenjun Natural Science Award, den ersten Preis der Provinz für Naturwissenschaften und andere Auszeichnungen und hat junge Talente auf nationaler Ebene wie Liang Xiaodan und Wang Keze ausgebildet .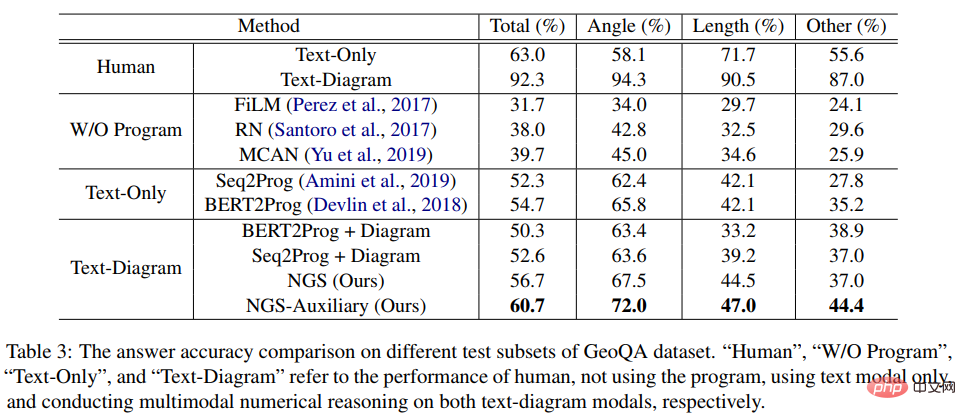 
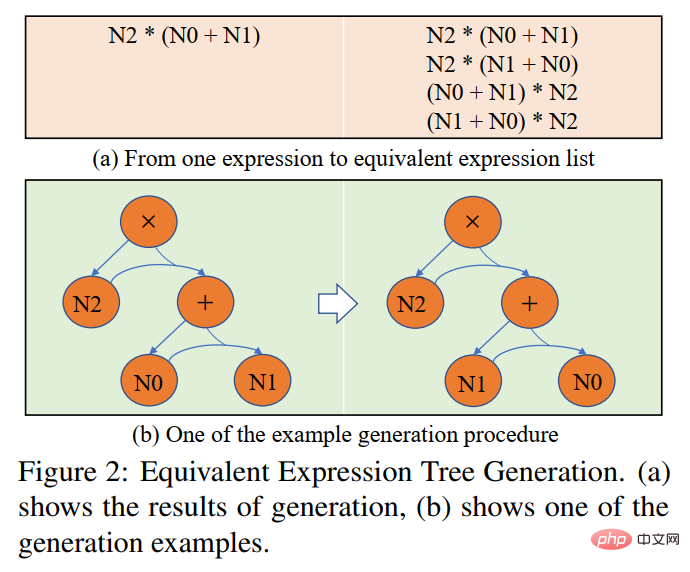
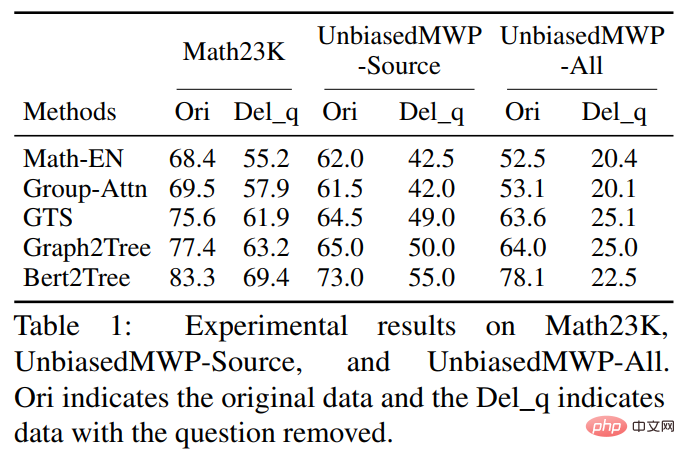
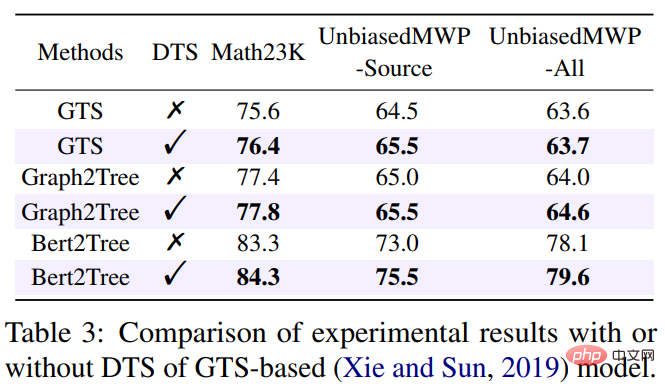
In den Experimenten haben wir mehrere Basismodelle auf dem InterMWP-Datensatz erstellt und unseren LogicSolver mit diesen Basismodellen verglichen. Die experimentellen Ergebnisse sind in der folgenden Tabelle aufgeführt.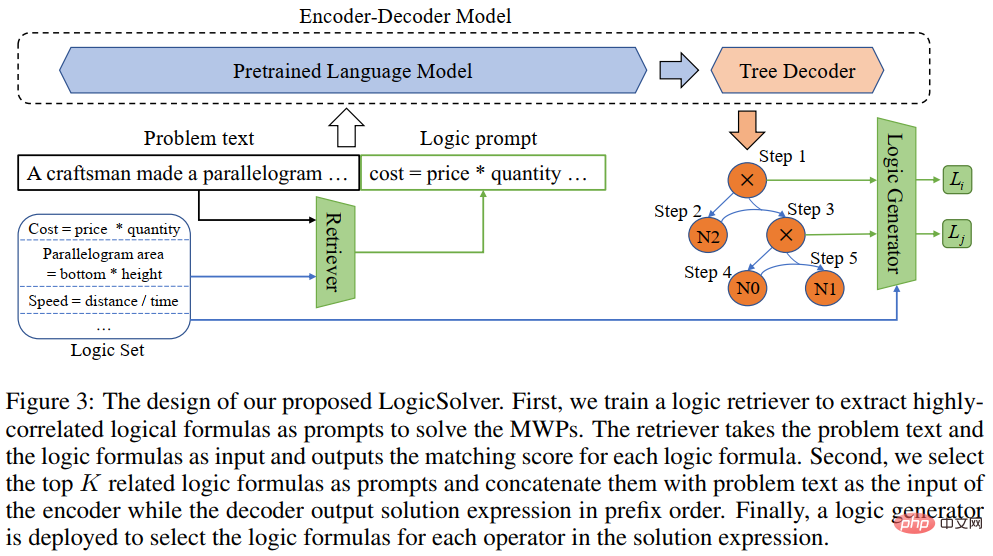 
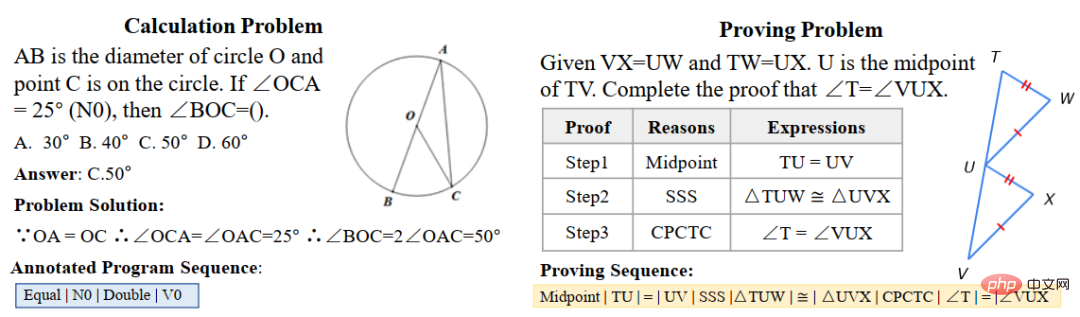
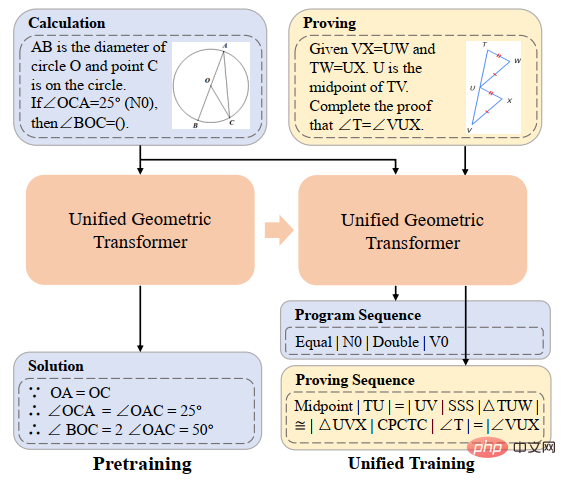
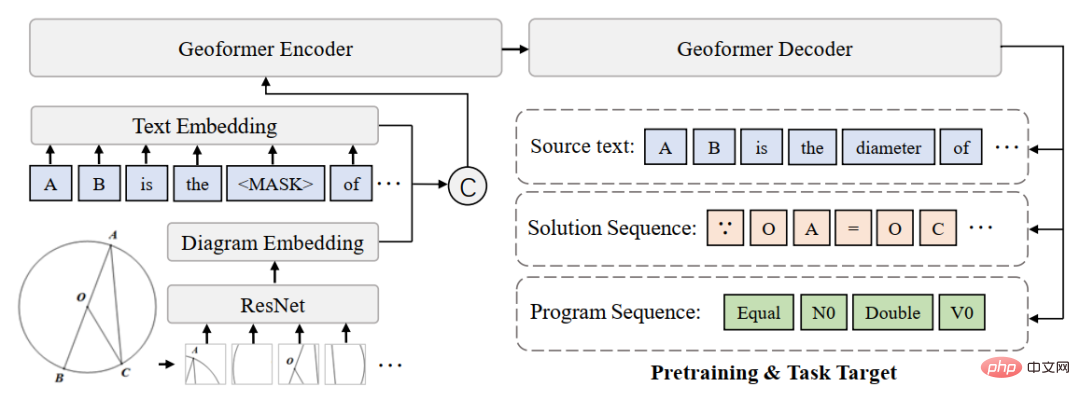
Das obige ist der detaillierte Inhalt vonHCP Lab-Team der Sun Yat-sen-Universität: Neue Durchbrüche bei der KI-Problemlösung und neuronalen Netzen öffnen die Tür zum mathematischen Denken. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
Der Unterschied zwischen mpvue und vue
So lösen Sie verstümmelte Zeichen in PHP
Was sind die SEO-Keyword-Ranking-Tools?
Können aufgeladene Telefonrechnungen von Douyin erstattet werden?
Mobile Festplattenpartitionssoftware
Das Anmeldetoken ist ungültig
Der Unterschied zwischen Pfeilfunktionen und gewöhnlichen Funktionen
So öffnen Sie eine MDS-Datei
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
