
Graphenbasiertes maschinelles Lernen hat in den letzten Jahren große Fortschritte gemacht. Graphbasierte Methoden finden bei vielen gängigen Problemen in der Datenwissenschaft Anwendung, wie z. B. Linkvorhersage, Community-Erkennung, Knotenklassifizierung usw. Es gibt viele Möglichkeiten, ein Problem zu lösen, je nachdem, wie Sie es organisieren und welche Daten Sie haben. Dieser Artikel bietet einen allgemeinen Überblick über graphbasierte Einbettungsalgorithmen. Abschließend stellen wir Ihnen auch vor, wie Sie Python-Bibliotheken (z. B. node2vec) verwenden, um verschiedene Einbettungen in Diagrammen zu generieren. Es gibt verschiedene Arten von Zweigen der künstlichen Intelligenz, die von Empfehlungssystemen, Zeitreihen, Verarbeitung natürlicher Sprache, Computer Vision, maschinellem Graphenlernen usw. reichen. Es gibt mehrere Möglichkeiten, häufige Probleme mit graphbasiertem maschinellen Lernen zu lösen. Einschließlich Community-Erkennung, Linkvorhersage, Knotenklassifizierung usw.
Ein großes Problem beim maschinellen Lernen mit Diagrammen besteht darin, eine Möglichkeit zu finden, die Diagrammstruktur darzustellen (oder zu kodieren), damit Modelle für maschinelles Lernen sie problemlos nutzen können [1]. Typischerweise erfordert die Lösung dieses Problems beim maschinellen Lernen das Erlernen einer Art Darstellung durch strukturierte Tabellendaten, die mit dem Modell verknüpft sind, was zuvor durch statistische Messungen oder Kernelfunktionen erfolgte. In den letzten Jahren ging der Trend dahin, Diagramme zu kodieren, um Einbettungsvektoren für das Training von Modellen für maschinelles Lernen zu generieren. 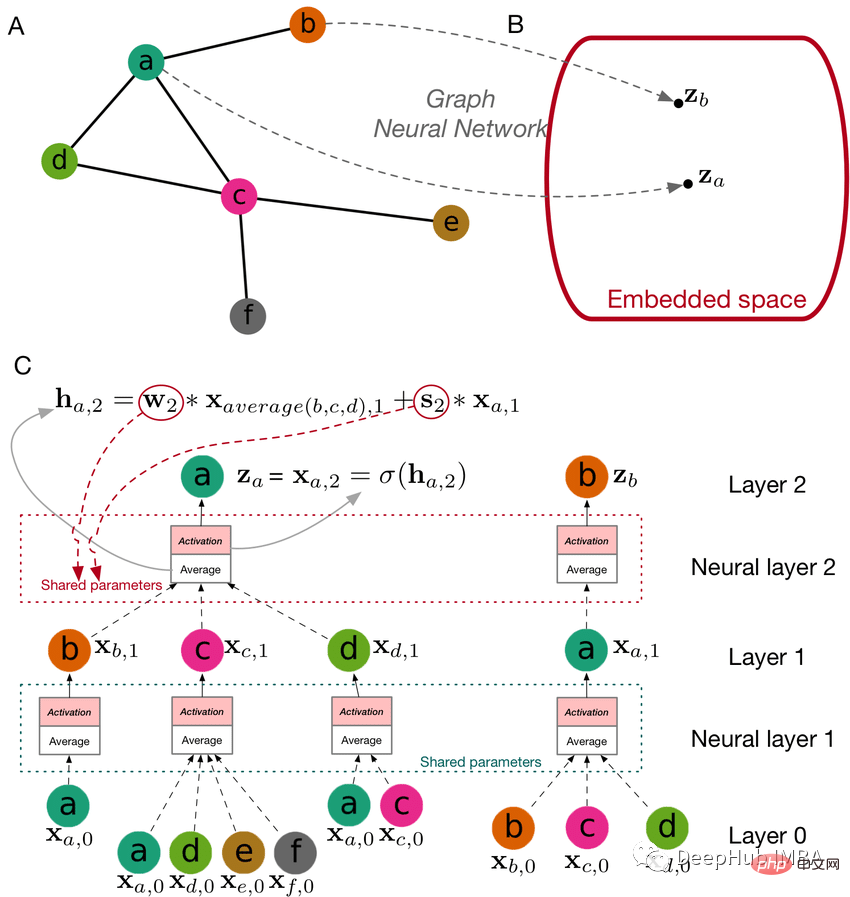
Wir könnten daran interessiert sein, demografische Informationen zu Benutzern in sozialen Netzwerken zu ermitteln. Zu den demografischen Daten gehören Alter, Geschlecht, Rasse usw. Soziale Netzwerke für Unternehmen wie Facebook oder Twitter umfassen Millionen bis Milliarden Nutzer und Billionen Seiten. Es wird definitiv mehrere Muster im Zusammenhang mit der Demografie der Benutzer in diesem Netzwerk geben, die für Menschen oder Algorithmen nicht leicht erkennbar sind, aber das Modell sollte in der Lage sein, sie zu lernen. In ähnlicher Weise möchten wir möglicherweise zwei Benutzern empfehlen, Freunde zu werden, die jedoch noch keine Freunde sind. Dies liefert Futter für die Linkvorhersage, eine weitere Anwendung des graphbasierten maschinellen Lernens.
Feature Engineering bezieht sich auf die gängige Methode zur Verarbeitung von Eingabedaten, um eine Reihe von Features zu bilden, die eine kompakte und aussagekräftige Darstellung des Originaldatensatzes liefern. Die Ergebnisse der Feature-Engineering-Phase dienen als Input für das maschinelle Lernmodell. Bei der Arbeit mit tabellarisch strukturierten Datensätzen ist dies ein notwendiger Prozess, bei der Arbeit mit Diagrammdaten jedoch ein schwieriger Ansatz, da eine Möglichkeit gefunden werden muss, eine geeignete Darstellung für alle Diagrammdaten zu generieren.
Es gibt viele Möglichkeiten, Features zu generieren, die Strukturinformationen aus Diagrammen darstellen. Die gebräuchlichste und einfachste Methode besteht darin, Statistiken aus einem Diagramm zu extrahieren. Dazu können Erkennungsverteilung, Seitenrang, Zentralitätsmetriken, Jaccard-Score usw. gehören. Die benötigten Attribute werden dann über eine Kernel-Funktion in das Modell eingearbeitet, allerdings besteht bei Kernel-Funktionen das Problem, dass der damit verbundene Zeitaufwand für die Generierung der Ergebnisse hoch ist.
Neueste Forschungstrends haben sich der Suche nach aussagekräftigen Diagrammdarstellungen und der Generierung eingebetteter Darstellungen für Diagramme zugewandt. Diese Einbettungen erlernen Diagrammdarstellungen, die die ursprüngliche Struktur des Netzwerks bewahren. Wir können es uns als eine Abbildungsfunktion vorstellen, die dazu dient, einen diskreten Graphen in einen kontinuierlichen Bereich umzuwandeln. Sobald eine Funktion gelernt ist, kann sie auf ein Diagramm angewendet werden und die resultierende Zuordnung kann als Funktionssatz für Algorithmen für maschinelles Lernen verwendet werden.
Arten der Diagrammeinbettung
Knoteneinbettung
Generieren Sie auf Knotenebene einen Einbettungsvektor, der jedem Knoten im Diagramm zugeordnet ist. Dieser Einbettungsvektor kann die Darstellung und Struktur des Diagramms berücksichtigen. Im Wesentlichen sollten Knoten, die nahe beieinander liegen, auch Vektoren haben, die nahe beieinander liegen. Dies ist eines der Grundprinzipien beliebter Knoteneinbettungsmodelle wie Node2Vec.
Kanteneinbettung In der Kantenebene wird ein Einbettungsvektor für jede Kante im Diagramm generiert. Das Link-Vorhersageproblem ist eine häufige Anwendung, die Kanteneinbettung verwendet. Unter Link-Vorhersage versteht man die Vorhersage der Wahrscheinlichkeit, ob eine Kante ein Knotenpaar verbindet. Diese Einbettungen können vom Diagramm bereitgestellte Kanteneigenschaften lernen. Beispielsweise können Sie in einem Diagramm eines sozialen Netzwerks ein Diagramm mit mehreren Kanten haben, in dem Knoten durch Kanten verbunden werden können, basierend auf Altersgruppe, Geschlecht usw. Diese Kanteneigenschaften können durch Darstellung des Korrelationsvektors der Kante gelernt werden.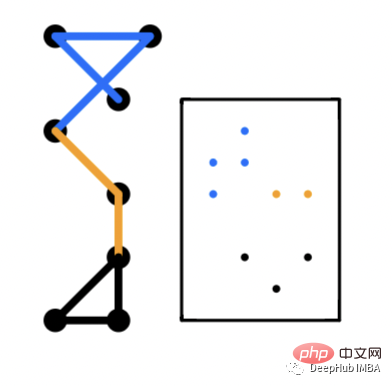
Einbettungen auf Diagrammebene sind ungewöhnlich. Sie bestehen aus der Generierung eines Einbettungsvektors, der jedes Diagramm darstellt. Beispielsweise verfügt in einem großen Diagramm mit mehreren Untergraphen jeder entsprechende Untergraph über einen Einbettungsvektor, der die Diagrammstruktur darstellt. Klassifizierungsprobleme sind eine häufige Anwendung, bei der die Einbettung von Graphen nützlich sein kann. Bei dieser Art von Problemen geht es darum, Diagramme in bestimmte Kategorien zu klassifizieren.
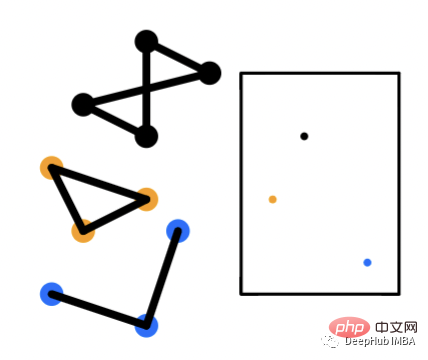
Verwenden Sie Python-Code, um die folgenden von uns benötigten Bibliotheken zu implementieren
Pythnotallow=3.9 networkx>=2.5 pandas>=1.2.4 numpy>=1.20.1 node2vec>=0.4.4 karateclub>=1.3.3 matplotlib>=3.3.4
Wenn Sie das node2vec-Paket nicht installiert haben, lesen Sie bitte die Dokumentation. Die Installation des Karateclub-Pakets ähnelt der Knoteneinbettung , usw. Hier wird node2vec verwendet. „Edge Embedding“: /edges .py#L91).
import random
import networkx as nx
import matplotlib.pyplot as plt
from node2vec import Node2Vec
from node2vec.edges import HadamardEmbedder
from karateclub import Graph2Vec
plt.style.use("seaborn")
# generate barbell network
G = nx.barbell_graph(
m1 = 13,
m2 = 7
)
# node embeddings
def run_n2v(G, dimensions=64, walk_length=80, num_walks=10, p=1, q=1, window=10):
"""
Given a graph G, this method will run the Node2Vec algorithm trained with the
appropriate parameters passed in.
Args:
G (Graph) : The network you want to run node2vec on
Returns:
This method will return a model
Example:
G = np.barbell_graph(m1=5, m2=3)
mdl = run_n2v(G)
"""
mdl = Node2Vec(
G,
dimensions=dimensions,
walk_length=walk_length,
num_walks=num_walks,
p=p,
q=q
)
mdl = mdl.fit(window=window)
return mdl
mdl = run_n2v(G)
# visualize node embeddings
x_coord = [mdl.wv.get_vector(str(x))[0] for x in G.nodes()]
y_coord = [mdl.wv.get_vector(str(x))[1] for x in G.nodes()]
plt.clf()
plt.scatter(x_coord, y_coord)
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Node2Vec Algorithm on Barbell Network")
plt.show()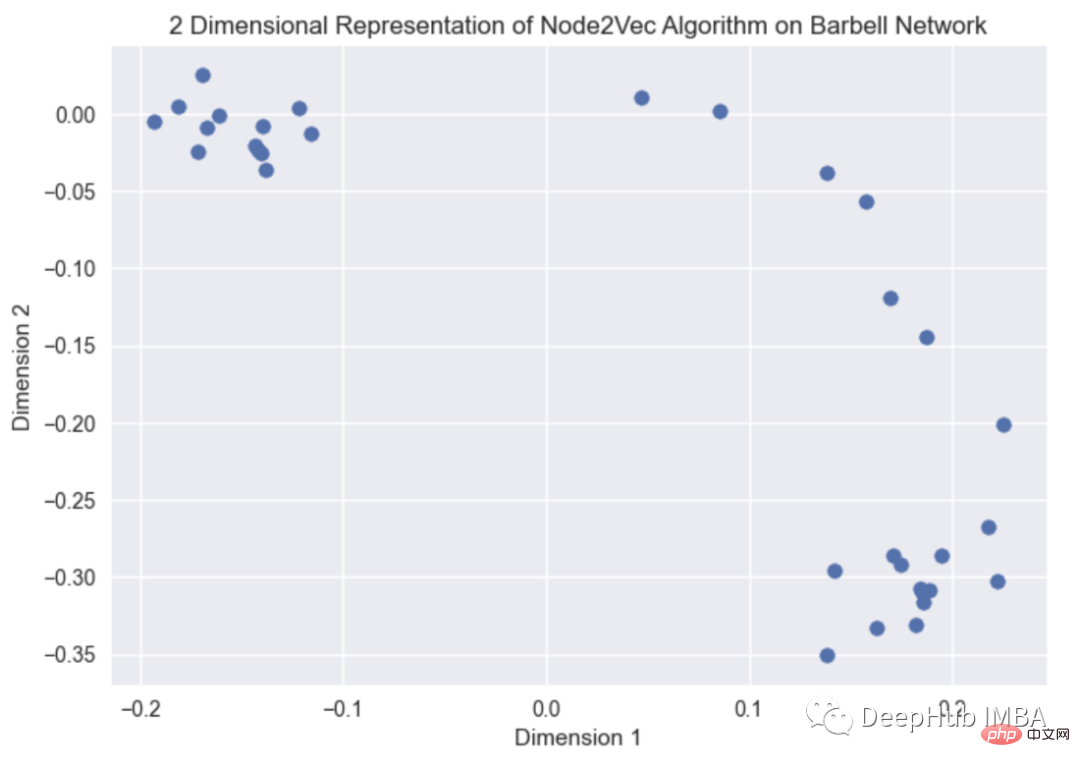
Dies ist eine Grafikeinbettungsvisualisierung von zufällig generierten Grafiken. Den Quellcode des graph2vec-Algorithmus finden Sie hier. (https://karateclub.readthedocs.io/en/latest/_modules/karateclub/graph_embedding/graph2vec.html)
Embedding ist eine Funktion, die diskrete Diagramme Vektordarstellungen zuordnet. Aus Diagrammdaten können verschiedene Formen von Einbettungen generiert werden: Knoteneinbettungen, Kanteneinbettungen und Diagrammeinbettungen. Alle drei Einbettungsarten bieten eine Vektordarstellung, die die anfängliche Struktur und die Merkmale des Diagramms auf numerische Werte in der X-Dimension abbildet.
Das obige ist der detaillierte Inhalt vonÜberblick über das Einbetten von Graphen: Methoden zum Einbetten von Knoten, Kanten und Graphen sowie Python-Implementierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




