Mathematische Programmierlöser werden aufgrund ihrer Bedeutung und Vielseitigkeit im Bereich Operations Research und Optimierung als „Lithographiemaschinen“ bezeichnet.
Unter diesen ist die Mixed-Integer Linear Programming (MILP) eine Schlüsselkomponente mathematischer Programmierlöser und kann eine Vielzahl praktischer Anwendungen modellieren, wie z. B. industrielle Produktionsplanung, Logistikplanung, Chipdesign, Pfadplanung, Finanzinvestitionen usw . Hauptbereiche.
Kürzlich haben das Team von Professor Wang Jie am MIRA Lab der Universität für Wissenschaft und Technologie von China und das Noah's Ark Laboratory von Huawei gemeinsam das Hierarchical Sequence Model (HEM) vorgeschlagen, das die Lösungseffizienz des gemischt-ganzzahligen linearen Programmierlösers erheblich verbessert. Die entsprechenden Ergebnisse wurden im ICLR 2023 veröffentlicht.
Derzeit ist der Algorithmus in Huaweis MindSpore ModelZoo-Modellbibliothek integriert, und verwandte Technologien und Funktionen werden noch in diesem Jahr in Huaweis OptVerse AI Solver integriert. Dieser Solver zielt darauf ab, Operations Research und KI zu kombinieren, um die Optimierungsgrenzen der Operational Research in der Branche zu durchbrechen, Unternehmen bei quantitativen Entscheidungen und verfeinerten Abläufen zu unterstützen und Kostensenkungen und Effizienzsteigerungen zu erreichen!
Autorenliste: Wang Zhihai*, Li Xijun*, Wang Jie**, Kuang Yufei, Yuan Mingxuan, Zeng Jia, Zhang Yongdong, Wu Feng
Link zum Papier: https://openreview.net/ forum?id=Zob4P9bRNcK
Open-Source-Datensatz: https://drive.google.com/drive/folders/1LXLZ8vq3L7v00XH-Tx3U6hiTJ79sCzxY?usp=sharing
PyTorch-Version Open-Source-Code: https://github.com/MIRALab -USTC/L2O-HEM- Torch
MindSpore-Version, offener Quellcode: https://gitee.com/mindspore/models/tree/master/research/l2o/hem-learning-to-cut
Tianchou (OptVerse) AI Solver: https://www.huaweicloud.com/product/modelarts/optverse.html
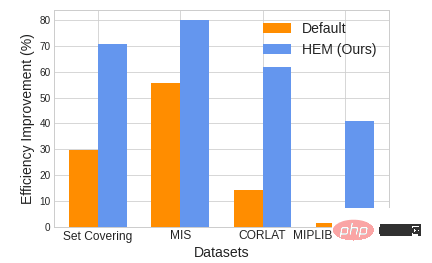
Abbildung 1. Vergleich der Lösungseffizienz zwischen HEM und der Solver-Standardstrategie (Standard). um bis zu 47,28 %
Schnittebenen (Schnitte) sind entscheidend für die effiziente Lösung gemischt-ganzzahliger linearer Programmierprobleme.
Die Schnittebenenauswahl (Schnittauswahl) zielt darauf ab, eine geeignete Teilmenge der auszuwählenden Schnittebenen auszuwählen, um die Effizienz der Lösung von MILP zu verbessern. Die Auswahl der Schnittebene hängt stark von zwei Teilproblemen ab: (P1) welche Schnittebenen bevorzugt werden sollten und (P2) wie viele Schnittebenen ausgewählt werden sollten.
Während viele moderne MILP-Löser (P1) und (P2) mit manuell entworfenen Heuristiken verarbeiten, haben maschinelle Lernmethoden das Potenzial, effizientere Heuristiken zu erlernen.
Viele bestehende Lernmethoden konzentrieren sich jedoch darauf, zu lernen, welche Schnittebenen priorisiert werden sollten, ignorieren jedoch das Lernen, wie viele Schnittebenen ausgewählt werden sollten. Darüber hinaus haben wir anhand einer Vielzahl experimenteller Ergebnisse beobachtet, dass ein weiteres Teilproblem, nämlich (P3), welche Reihenfolge der Schnittebenen bevorzugt werden sollte, ebenfalls einen erheblichen Einfluss auf die Effizienz der Lösung von MILP hat.
Um diese Herausforderungen anzugehen, schlagen wir ein neuartiges hierarchisches Sequenzmodell (HEM) vor und erlernen die Strategie zur Auswahl der Schnittebene durch ein Rahmenwerk für verstärkendes Lernen.
Nach unserem besten Wissen ist HEM die erste Lernmethode, die (P1), (P2) und (P3) gleichzeitig verarbeiten kann. Experimente zeigen, dass HEM die Effizienz der Lösung von MILP im Vergleich zu manuell entworfenen und erlernten Basislinien auf künstlich generierten und groß angelegten MILP-Datensätzen aus der realen Welt erheblich verbessert.
Mixed-Integer Linear Programming (MILP) ist ein allgemeines Optimierungsmodell, das in einer Vielzahl praktischer Anwendungsbereiche, wie beispielsweise dem Supply Chain Management, weit verbreitet eingesetzt werden kann [1], Produktionsplanung [2], Planung und Versand [3], Auswahl des Fabrikstandorts [4], Verpackungsproblem [5] usw.
Das Standard-MILP hat die folgende Form:
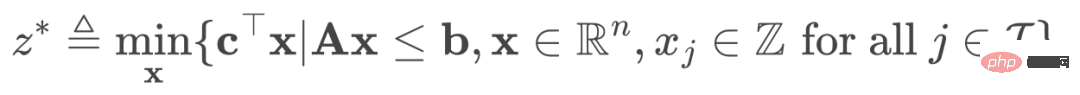
(1)
Gegebenes Problem (1) verwerfen wir alle seine ganzzahligen Einschränkungen und erhalten das Problem der linearen Programmierrelaxation (LPR). Seine Form ist:
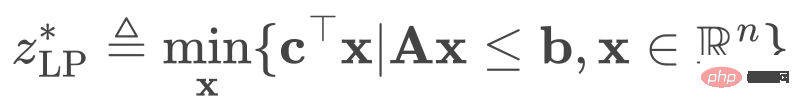
(2)
Da Problem (2) die zulässige Menge von Problem (1) erweitert, können wir annehmen, dass der optimale Wert des LPR-Problems das ursprüngliche MILP-Problem Nether ist.
Angesichts des LPR-Problems in (2) sind Schnittebenen (Schnitte) eine Klasse legaler linearer Ungleichungen, die, wenn sie zum Relaxationsproblem der linearen Programmierung hinzugefügt werden, den zulässigen Domänenraum im LPR-Problem verkleinern und keine entfernen können ganzzahlige zulässige Lösungen für das ursprüngliche MILP-Problem.
Der MILP-Löser kann im Prozess der Lösung des MILP-Problems eine große Anzahl von Schnittebenen generieren und fügt dem ursprünglichen Problem in aufeinanderfolgenden Runden weiterhin Schnittebenen hinzu.
Im Einzelnen umfasst jede Runde fünf Schritte:
(1) Lösen Sie das aktuelle LPR-Problem;
(2) Erzeugen Sie eine Reihe auszuwählender Schnittebenen;
(3) Wählen Sie aus den auszuwählenden Schnittebenen a geeignete Teilmenge;
(4) Fügen Sie die ausgewählte Teilmenge zum LPR-Problem in (1) hinzu, um ein neues LPR-Problem zu erhalten.
(5) Wiederholen Sie den Zyklus, basierend auf dem neuen LPR-Problem, und geben Sie die nächste Runde ein.
Durch das Hinzufügen aller generierten Schnittebenen zum LPR-Problem wird der realisierbare Regionsraum des Problems so weit wie möglich verkleinert, um die Untergrenze zu maximieren.
Das Hinzufügen zu vieler Schnittebenen kann jedoch dazu führen, dass das Problem zu viele Einschränkungen aufweist, den Rechenaufwand für die Problemlösung erhöht und numerische Instabilität verursacht [6,7].
Daher haben Forscher die Auswahl der Schnittebene (Schnittauswahl) vorgeschlagen, die darauf abzielt, eine geeignete Teilmenge der Kandidaten-Schnittebenen auszuwählen, um die Effizienz der MILP-Problemlösung so weit wie möglich zu verbessern. Die Auswahl der Schnittebene ist entscheidend für die Verbesserung der Effizienz bei der Lösung gemischter ganzzahliger linearer Programmierprobleme [8, 9, 10].
Wir haben zwei heuristische Algorithmen für die Auswahl von Schnittebenen entworfen, nämlich RandomAll und RandomNV (Einzelheiten finden Sie in Kapitel 3 des Originalpapiers).
Sie alle fügen die ausgewählten Schnitte in zufälliger Reihenfolge zum MILP-Problem hinzu, nachdem sie eine Reihe von Schnitten ausgewählt haben. Wie in den Ergebnissen in Abbildung 2 gezeigt, hat das Hinzufügen dieser ausgewählten Schnittebenen in unterschiedlicher Reihenfolge bei Auswahl derselben Schnittebene einen großen Einfluss auf die Lösungseffizienz des Lösers (eine detaillierte Ergebnisanalyse finden Sie in Kapitel 3 des Originalpapiers).
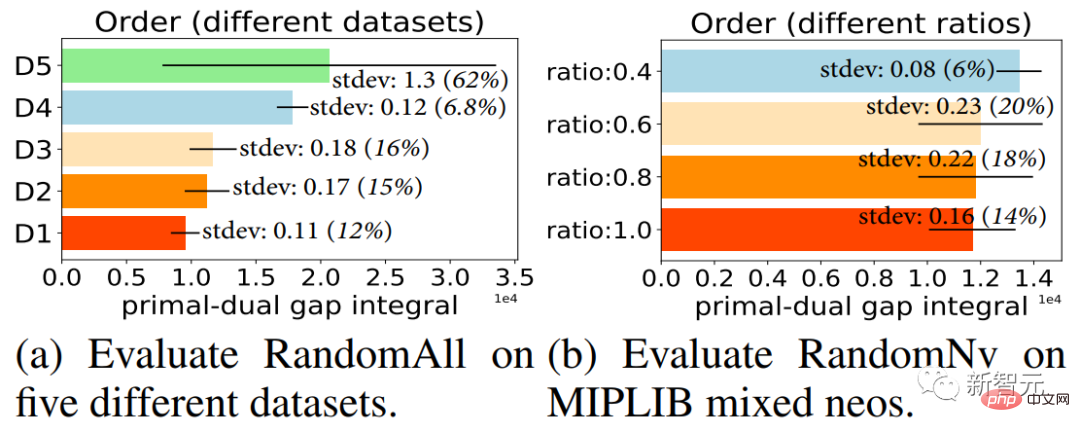
Abbildung 2. Jede Spalte stellt den Mittelwert der endgültigen Lösungseffizienz des Lösers dar, wenn der gleiche Stapel von Schnittebenen im Löser ausgewählt wird und diese ausgewählten Schnittebenen in 10 Runden unterschiedlicher Reihenfolge hinzugefügt werden Abweichungslinien in den Spalten stellen die Standardabweichung der Lösungseffizienz unter verschiedenen Ordnungen dar. Je größer die Standardabweichung ist, desto größer ist der Einfluss der Ordnung auf die Lösungseffizienz des Lösers.
Bei der Aufgabe zur Auswahl der Schnittebene kann die optimale Teilmenge, die ausgewählt werden sollte, nicht im Voraus ermittelt werden.
Wir können jedoch den Solver verwenden, um die Qualität einer beliebigen ausgewählten Teilmenge zu bewerten und diese Bewertung als Feedback für den Lernalgorithmus zu verwenden.
Daher verwenden wir das Reinforcement Learning (RL)-Paradigma, um die Strategie zur Auswahl der Schnittebene durch Versuch und Irrtum zu erlernen.
In diesem Abschnitt erläutern wir unser vorgeschlagenes RL-Framework.
Zuerst modellieren wir die Aufgabe zur Auswahl der Schnittebene als Markov-Entscheidungsprozess (MDP); dann stellen wir unser vorgeschlagenes hierarchisches Sequenzmodell (HEM) im Detail vor und leiten schließlich hierarchische Richtliniengradienten für ein effizientes Training von HEMs ab. Unser Gesamtdiagramm des RL-Rahmens ist in Abbildung 3 dargestellt.
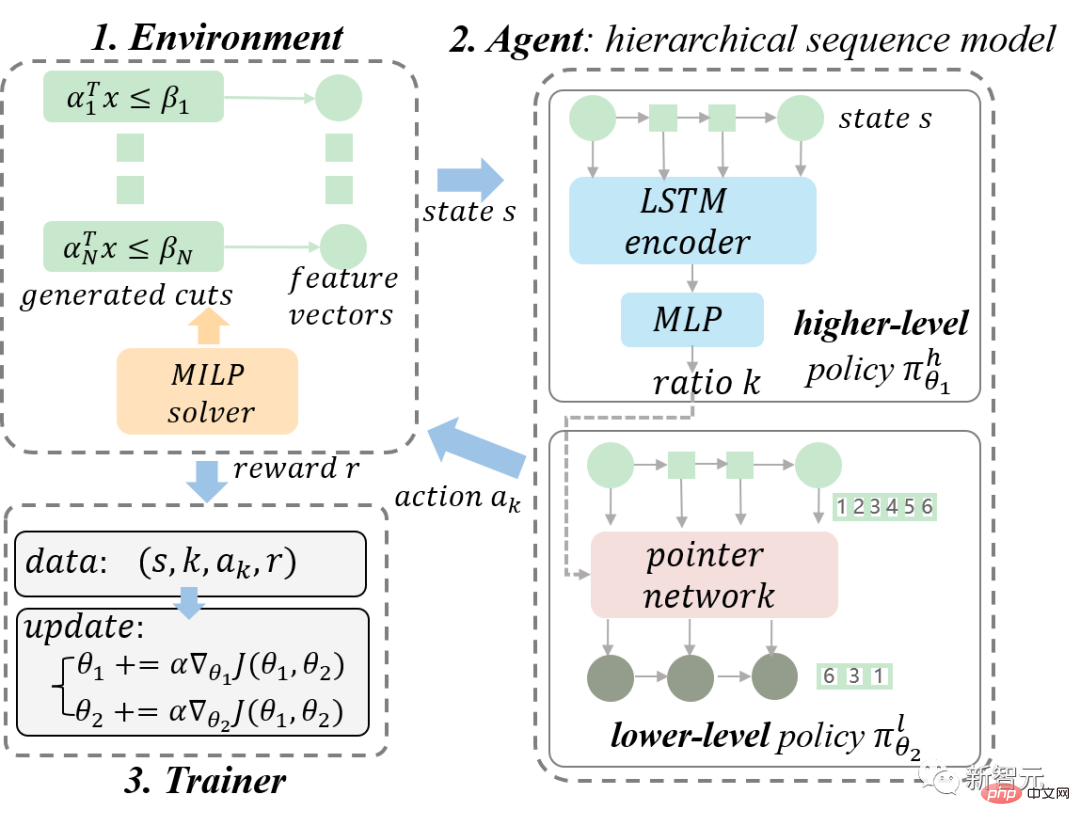
Abbildung 3. Diagramm unseres vorgeschlagenen RL-Gesamtrahmens. Wir modellieren den MILP-Löser als Umgebung und das HEM-Modell als Agent. Wir sammeln Trainingsdaten durch kontinuierliche Interaktion zwischen dem Agenten und der Umgebung und trainieren das HEM-Modell mithilfe eines hierarchischen Richtliniengradienten.
Zustandsraum: Da die aktuelle LP-Entspannung und die generierten Kandidatenschnitte die Kerninformationen der Schnittebenenauswahl enthalten, definieren wir den Zustand. Hier stellt das mathematische Modell der aktuellen LP-Relaxation dar, stellt die Menge der Kandidaten-Schnittebenen dar und stellt die optimale Lösung der LP-Relaxation dar. Um Zustandsinformationen zu kodieren, entwerfen wir basierend auf den Informationen 13 Merkmale für jede in Frage kommende Schnittebene. Das heißt, wir stellen den Zustand s durch einen 13-dimensionalen Merkmalsvektor dar. Weitere Einzelheiten finden Sie in Kapitel 4 des Originalartikels.
Aktionsraum: Um sowohl das Verhältnis als auch die Reihenfolge der ausgewählten Schnitte zu berücksichtigen, definieren wir den Aktionsraum als alle geordneten Teilmengen der Menge der Kandidatenschnitte.
Belohnungsfunktion: Um die Auswirkung des Hinzufügens von Schnitten auf die Lösung von MILP zu bewerten, können wir die Lösungszeit, das Primal-Dual-Gap-Integral und die Dual-Bound-Verbesserung verwenden. Weitere Einzelheiten finden Sie in Kapitel 4 des Originalartikels.
Übergangsfunktion: Die Übertragungsfunktion gibt den nächsten Zustand angesichts des aktuellen Zustands und der durchgeführten Aktion aus. Die Übertragungsfunktion in der Aufgabe zur Auswahl der Schnittebene wird implizit vom Löser bereitgestellt.
Weitere Modellierungsdetails finden Sie in Kapitel 4 des Originalartikels.
Wie in Abbildung 3 dargestellt, modellieren wir den MILP-Löser als Umgebung und den HEM als Agenten. Das vorgeschlagene HEM-Modell wird im Folgenden ausführlich vorgestellt. Um das Lesen zu erleichtern, vereinfachen wir die Motivation der Methode und konzentrieren uns auf die klare Erläuterung der Methodenimplementierung. Interessierte Leser können sich für relevante Details gerne auf Kapitel 4 des Originalpapiers beziehen.
Wie im Agentenmodul in Abbildung 3 dargestellt, besteht HEM aus oberen und unteren Richtlinienmodellen. Die Modelle der oberen und unteren Schicht lernen die Richtlinie der oberen Schicht (Richtlinie) bzw. die Richtlinie der unteren Schicht.
Zunächst lernt die übergeordnete Richtlinie die Anzahl der Kürzungen, die ausgewählt werden sollten, indem sie den entsprechenden Anteil vorhersagt. Unter der Annahme, dass die Zustandslänge ist und das Vorhersageverhältnis ist, dann ist die Anzahl der Schnitte, die für die Vorhersage ausgewählt werden sollten,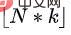 
, wobei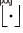 
die Abrundungsfunktion darstellt. Wir definieren 
.
Zweitens lernt die untergeordnete Richtlinie, eine geordnete Teilmenge einer bestimmten Größe auszuwählen. Die untergeordnete Richtlinie kann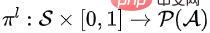 
definiert werden, wobei 
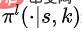die Wahrscheinlichkeitsverteilung über den Aktionsraum bei gegebenem Zustand S und dem Anteil K darstellt. Konkret modellieren wir die zugrunde liegende Richtlinie als Sequenz-zu-Sequenz-Modell (Sequenzmodell).
Schließlich wird die Schnittauswahlstrategie durch das Gesetz der Gesamtwahrscheinlichkeit abgeleitet, d . Hierarchischer Strategiegradient. Wir optimieren das HEM-Modell auf diese Weise mit stochastischem Gradientenabstieg.
4 Einführung in das Experiment
Unser Experiment besteht aus fünf Hauptteilen:
Experiment 4. Visualisieren Sie die Eigenschaften der durch unsere Methode und Basislinie ausgewählten Schnittebenen. 
Wir stellen in diesem Artikel nur Experiment 1 vor. Weitere experimentelle Ergebnisse finden Sie in Kapitel 5 des Originalpapiers. Bitte beachten Sie, dass alle in unserem Artikel berichteten experimentellen Ergebnisse Ergebnisse sind, die auf dem Training mit dem PyTorch-Versionscode basieren.
Das obige ist der detaillierte Inhalt vonKI-gesteuertes Operations Research optimiert „Lithographiemaschinen'! Die Universität für Wissenschaft und Technologie Chinas und andere schlugen ein hierarchisches Sequenzmodell vor, um die Effizienz der mathematischen Programmierlösung erheblich zu verbessern.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
location.hash
So verwenden Sie den ffdshow-Decoder
Warum startet mein Telefon ständig neu?
Was sind die Python-Bibliotheken für künstliche Intelligenz?
So lösen Sie Probleme beim Parsen von Paketen
So öffnen Sie eine DB-Datei
Was sind die CSS3-Gradienteneigenschaften?
Was ist eine NFC-Zugangskontrollkarte?
