 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Wie können Daten für kausale Schlussfolgerungen besser genutzt werden?
Wie können Daten für kausale Schlussfolgerungen besser genutzt werden?
Wie können Daten für kausale Schlussfolgerungen besser genutzt werden?

Einleitung: Der Titel dieser Weitergabe lautet „Wie können Daten bei kausalen Schlussfolgerungen besser genutzt werden?“ ", in dem hauptsächlich die jüngsten Arbeiten des Teams im Zusammenhang mit veröffentlichten Arbeiten zu Ursache und Wirkung vorgestellt werden. In diesem Bericht wird vorgestellt, wie wir mehr Daten verwenden können, um kausale Schlussfolgerungen aus zwei Aspekten zu ziehen: Zum einen können wir historische Kontrolldaten verwenden, um Verwirrungsverzerrungen explizit zu mildern, und zum anderen können wir kausale Schlussfolgerungen durch die Fusion von Daten aus mehreren Quellen ziehen.
Volltext-Inhaltsverzeichnis:
- Hintergrund der Kausalinferenz
- Korrigierter Kausalbaum GBCT
- Kausale Datenfusion
- Geschäftsanwendung in Ant ?? Bildklassifizierung usw. Frage. Bei der Frage nach der Kausalität geht es um den Mechanismus hinter den Daten. Häufige Fragen wie „Verursacht Rauchen Lungenkrebs?“ Ähnliche Fragen sind Kausalitätsfragen.
Beim Problem der Kausalwirkungsschätzung gibt es zwei sehr wichtige Datentypen: Ein Typ sind Beobachtungsdaten und der andere Typ sind experimentelle Daten, die durch randomisierte kontrollierte Experimente generiert werden.
Beobachtungsdaten sind die Daten, die in unserem tatsächlichen Leben oder in unseren Produkten gesammelt werden. Die Raucherdaten zeigen beispielsweise, dass manche Menschen gerne rauchen, während die Beobachtungsdaten sich auf Raucher beziehen. Am Ende erkranken einige der Raucher an Krebs. Das Problem der Vorhersage des maschinellen Lernens besteht darin, die bedingte Wahrscheinlichkeit P (Lungenkrebs bekommen | Rauchen) abzuschätzen, dh unter Berücksichtigung der Bedingungen des Rauchens die Wahrscheinlichkeit, dass ein Raucher an Lungenkrebs erkrankt. In den oben genannten Beobachtungsdaten ist die Verteilung des Rauchens tatsächlich nicht zufällig: Jeder Mensch hat eine andere Vorliebe für das Rauchen und wird auch von der Umgebung beeinflusst.
Der beste Weg, kausale Fragen zu beantworten, ist die Durchführung eines randomisierten kontrollierten Experiments. Experimentelle Daten werden durch randomisierte kontrollierte Experimente gewonnen. In einer randomisierten kontrollierten Studie erfolgt die Zuordnung zur Behandlung zufällig. Angenommen, Sie müssen ein Experiment durchführen, um die Schlussfolgerung zu erhalten, „ob Rauchen Lungenkrebs verursacht“. Zuerst müssen Sie genügend Menschen finden, die Hälfte von ihnen zum Rauchen zwingen und die andere Hälfte dazu zwingen, nicht zu rauchen, und die Wahrscheinlichkeit einer Lungenkrebserkrankung beobachten Krebs in beiden Gruppen. Obwohl randomisierte kontrollierte Studien in einigen Szenarien aufgrund von Faktoren wie Ethik und Richtlinien nicht möglich sind, können randomisierte kontrollierte Studien in einigen Bereichen dennoch durchgeführt werden, beispielsweise bei A/B-Tests in der Suchmaschinenwerbung.
- Der Hauptunterschied zwischen dem Kausalschätzproblem E(Y|do(X)) und dem traditionellen Vorhersage- oder Klassifizierungsproblem E(Y|X) besteht darin, dass: gegebene Bedingungen entstehen. Die von vorgeschlagene Intervention Judy Pearl repräsentiert das Symbol Do. Greifen Sie ein, um die X-Variable auf einen bestimmten Wert zu zwingen. Die Schätzung der kausalen Wirkungen in diesem Bericht bezieht sich hauptsächlich auf die Schätzung der kausalen Wirkungen anhand von Beobachtungsdaten.
 Wie können Daten besser für kausale Schlussfolgerungen genutzt werden? In diesem Bericht wird ein solches Thema anhand aktueller, von zwei Teams veröffentlichter Arbeiten als Beispiele vorgestellt.
Wie können Daten besser für kausale Schlussfolgerungen genutzt werden? In diesem Bericht wird ein solches Thema anhand aktueller, von zwei Teams veröffentlichter Arbeiten als Beispiele vorgestellt.
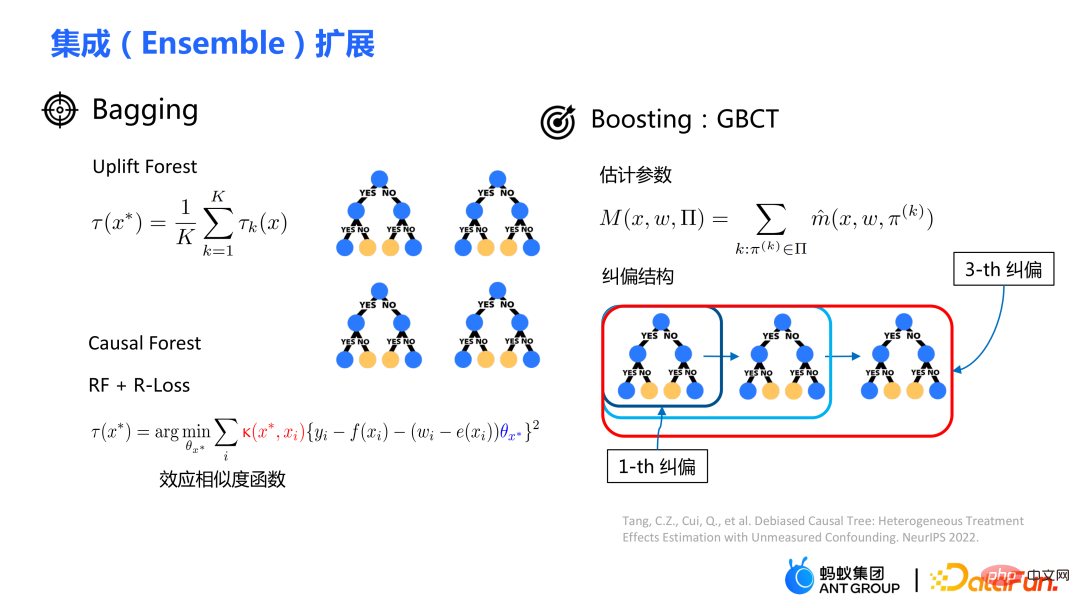
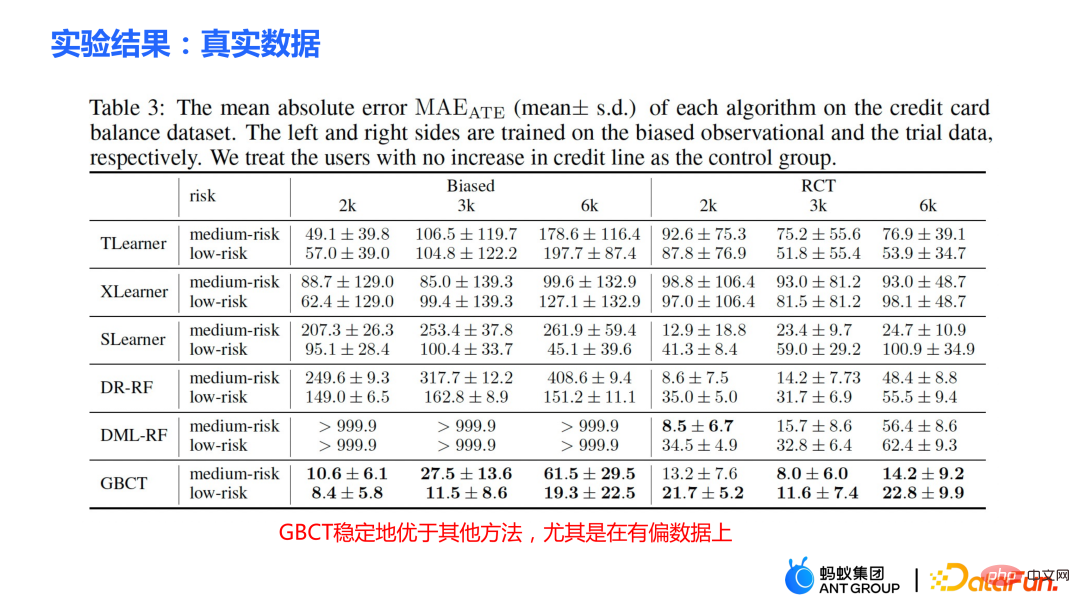
Der Baumalgorithmus besteht hauptsächlich aus zwei Modulen: Die übliche Methode zur Parameterschätzung besteht darin, das durchschnittliche Ergebnis der Kontrollgruppe direkt vom durchschnittlichen Ergebnis der Versuchsgruppe auf dem Split-Blatt-Knoten zu subtrahieren. als Schätzungen kausaler Wirkungen. Wenn es sich um ein randomisiertes kontrolliertes Experiment handelt, ist der Zuordnungsmechanismus für die Behandlung zufällig und die daraus berechnete durchschnittliche Differenz ist der kausale Effekt. Der Zufallszuteilungsmechanismus stellt sicher, dass die Datenverteilung der Versuchsgruppe und der Kontrollgruppe gleich ist, was als Homogenität bezeichnet wird. Weitere traditionelle kausale Effekte können Split geschätzt werden in zwei Teile: Selektionsbias/Confoundingbias kann definiert werden als: Die intuitive Bedeutung ist der geschätzte Wert, wenn Behandlung = 0 in der Versuchsgruppe, abzüglich des geschätzten Werts, wenn Behandlung = 0 in der Kontrollgruppe . In traditionellen Kausalbäumen ist die obige Verzerrung nicht charakterisiert, und die Auswahlverzerrung kann unsere Schätzungen beeinflussen und dazu führen, dass die endgültige Schätzung verzerrt ist. Die Integration traditioneller Baummodelle umfasst Methoden wie Bagging und Boosting. Die von Uplift Forest oder Causal Forest verwendete Integrationsmethode ist die Bagging-Methode. Die Integration von Uplift Forest ist eine direkte Summierung, während die Integration von Causal Forest die Lösung einer Verlustfunktion erfordert. Aufgrund des in GBCT entwickelten expliziten Korrekturmoduls unterstützt GBCT die Integration mithilfe der Boosting-Methode. Die Grundidee ähnelt dem Boosten: Nachdem der erste Baum korrigiert wurde, wird der zweite Baum korrigiert und der dritte Baum wird korrigiert ... Es wurden zwei Teile des Experiments durchgeführt: ① Simulationsexperiment. Testen Sie anhand von Simulationsexperimenten mit Ground Truth, ob die GBCT-Methode die erwarteten Ergebnisse erzielen kann. Die Datengenerierung für das Simulationsexperiment ist in zwei Teile unterteilt (die erste Spalte Φ in der Tabelle stellt die Auswahlverzerrung dar. Je größer der Φ-Wert, desto stärker die entsprechende Auswahlverzerrung; der Wert in der Tabelle ist MAE. Je kleiner der MAE-Wert , desto besser die Methode) : ② Echte Daten zur Erhöhung des Kreditkartenlimits. Es wurde ein randomisiertes, kontrolliertes Experiment durchgeführt und auf der Grundlage des randomisierten, kontrollierten Experiments wurden voreingenommene Daten erstellt. In verschiedenen Umgebungen übertrifft die GBCT-Methode durchweg herkömmliche Methoden, insbesondere bei verzerrten Daten, und schneidet deutlich besser ab als herkömmliche Methoden. Die zweite Aufgabe ist die kausale Datenfusion, das heißt, wenn mehrere Datenquellen vorhanden sind Situation, wie man kausale Auswirkungen besser abschätzen kann. Die Hauptsymbole: sind mehrere Datenquellen, Y ist das Ergebnis, A ist die Behandlung, X ist die interessierende Kovariate, Z sind die anderen Kovariaten jeder Datenquelle (Domäne) außer Zerlegen Sie das Ergebnis in den folgenden Ausdruck: Zielfunktion δ wird als Schätzung verwendet die kausale Wirkung auf jede Domäne. Darüber hinaus umfassen Störfunktionen Haupteffekte, Neigungswerte, Domänenneigungswerte, Varianzen von Effekten usw. Einige traditionelle Methoden, wie Meta-Learner usw., gehen alle davon aus Die Daten sind homolog, d. h. die Verteilung ist konsistent. Einige herkömmliche Datenfusionsmethoden können die Heterogenität von Populationen über Domänen hinweg bewältigen, können jedoch die Heterogenität von Interventionsergebnissen und kausalen Effekten über Domänen hinweg nicht explizit erfassen. Unsere Arbeit konzentriert sich auf den Umgang mit komplexerer domänenübergreifender Heterogenität, einschließlich domänenübergreifender Heterogenität bei Interventionsergebnissen und domänenübergreifender Heterogenität bei kausalen Effekten. Das Rahmendiagramm des WMDL-Algorithmus ist in der Abbildung oben dargestellt. Die Hauptmodule sind: Die drei Module werden kombiniert, um den endgültigen Kostenvoranschlag zu erhalten. Die drei Highlights des WMDL-Algorithmus sind: Die Formel wird auf der Grundlage der Zerlegungsformel abgeleitet. Ergebnis Y minus Haupteffekt dividiert durch Behandlung wird auf I(X) geschätzt, und die erhaltene optimale Lösung ist δ(X). Der Zähler in Diese Arbeit hat drei Vorteile: ① Durch unterschiedliche Designs kann sie nicht nur mit der Heterogenität der Interventionsergebnisse umgehen, sondern auch mit der Heterogenität der kausalen Wirkungen; von doppelter Robustheit. In der Arbeit wird der Beweis erbracht, dass die endgültige Schätzung unverzerrt sein wird, solange die Schätzung entweder des Propensity-Score-Modells der Domäne oder des Haupteffektmodells unvoreingenommen ist (die tatsächliche Situation ist etwas komplizierter, Einzelheiten finden Sie in der Arbeit). ; ③ Diese Arbeit entwirft hauptsächlich das semiparametrische Modellgerüst. Jedes Modul des Modells kann ein beliebiges Modell für maschinelles Lernen verwenden, und das gesamte Modell kann sogar in ein neuronales Netzwerk integriert werden, um ein durchgängiges Lernen zu erreichen. Das Modul der Gewichtung ist aus der Effizienzschrankentheorie der Statistik abgeleitet. Es enthält hauptsächlich zwei Informationsaspekte: ist ein Modul zur ausgewogenen Umrechnung von Verteilungsunterschieden zwischen Domänen; Durch die geschickte Kombination der oben genannten drei Teile können die Verteilungsunterschiede zwischen verschiedenen Domänen und die Leistung verschiedener Kausalinformationen in einer einheitlichen Domäne abgebildet werden. Unabhängig von homogenen Kausaleffekten oder heterogenen Kausaleffekten erzielt die WMDL-Methode (Weighted Multi-domain Direct Learning) bessere Ergebnisse. Das Bild rechts zeigt ein Ablationsexperiment am Gewichtungsmodul. Das Experiment zeigt die Wirksamkeit des Gewichtungsmoduls. Zusammenfassend lässt sich sagen, dass die WMDL-Methode durchweg eine bessere Leistung als andere Methoden erbringt und die geschätzte Varianz relativ gering ist. 4. Geschäftsanwendungen in Ant In Szenarien zur finanziellen Kreditrisikokontrolle wird erwartet, dass Interventionsmethoden wie Quotenerhöhungen und Preissenkungen erwartete Effekte wie Salden- oder Risikoänderungen erzielen. In einigen tatsächlichen Szenarien wird die GBCT-Korrekturarbeit die historische Leistung in der Zeit vor der Stirnstraffung nutzen (der Status der Versuchsgruppe und der Kontrollgruppe ohne Stirnstraffung kann ermittelt werden) und eine explizite Korrektur anhand historischer Informationen durchführen dass der Eingriff spätere Schätzungen genauer sein werden. Wenn GBCT in einen untergeordneten Knoten aufgeteilt wird, sodass die Verhaltensweisen vor dem Eingriff angeglichen werden, lässt sich der kausale Effekt nach dem Eingriff leichter abschätzen. (Erhalten nach der Korrektur) In der Abbildung ist die rote Farbe die Gruppe, die die Stirn hebt, die blaue Farbe ist die Gruppe, in der die Stirn nicht gehoben wird, und der graue Bereich in der Mitte ist der geschätzte kausale Effekt. GBCT hilft uns, bessere, intelligente Entscheidungen zu treffen und das Gleichgewicht und die Risiken von Kreditprodukten zu kontrollieren. A1: Die Hauptidee der GBCT-Korrektur besteht darin, historische Kontrollinformationen zu verwenden, um den Auswahlfehler explizit zu reduzieren. Die GBCT-Methode und die DID-Doppeldifferenzmethode weisen Ähnlichkeiten und Unterschiede auf: A2: Wenn alle Störvariablen beobachtet wurden und die Annahme der Ignorierbarkeit erfüllen, ist es bis zu einem gewissen Grad möglich, dass die Versuchsgruppe und die Kontrollgruppe durch herkömmliche Methoden getrennt werden, auch wenn der Selektionsbias nicht explizit reduziert wird Um eine Ausrichtung zu erreichen, zeigen Experimente, dass GBCT eine etwas bessere Leistung erbringt und die Ergebnisse durch explizite Korrektur stabiler sind. Gehen Sie davon aus, dass es in der Praxis einige unbeobachtete Störvariablen gibt, wie z. B. die Familiensituation und das Einkommen, bevor die Quote erhöht wird nicht beobachtet werden, aber das Finanzverhalten der Nutzer spiegelt sich in historischen Daten wider. Wir hoffen, die Auswahlverzerrung durch Methoden wie Verwirrungsentropie anhand historischer Leistungsinformationen explizit zu reduzieren, sodass beim Teilen des Baums die Heterogenität zwischen verwirrenden Variablen in den geteilten untergeordneten Knoten charakterisiert werden kann. Unter den untergeordneten Knoten liegen die unbeobachteten Störvariablen relativ nahe beieinander, sodass sie eine größere Wahrscheinlichkeit haben, sodass die geschätzten kausalen Effekte relativ genauer sind. A3: Ich habe einen Vergleich gemacht. Double Machine Learning ist eine semiparametrische Methode. Unsere Arbeit in diesem Artikel konzentriert sich mehr auf baumbasierte Methoden, sodass die ausgewählten Basislerner baum- oder waldbezogene Methoden sind. DML-RF in der Tabelle ist die Double Machine Learning-Version von Random Forest. Im Vergleich zu DML berücksichtigt GBCT hauptsächlich die Verwendung historischer Vergleichsdaten. Bei der Vergleichsmethode wird das historische Ergebnis direkt als Kovariate verarbeitet, diese Verarbeitungsmethode nutzt die Informationen jedoch offensichtlich nicht optimal aus. A4: Dieses Problem ist ein sehr wesentliches Problem in der Finanzszene. Bei der Suchmaschinenwerbung kann der Unterschied zwischen Offline und Online teilweise durch Online-Lernen oder A/B-Tests überwunden werden. In Finanzszenarien ist es aufgrund des politischen Einflusses nicht einfach, Experimente online durchzuführen. Außerdem dauert die Beobachtung der Leistung von Kreditprodukten mindestens einen Monat. Daher ist es tatsächlich sehr schwierig, dieses Problem perfekt zu lösen. Wir verwenden im Allgemeinen die folgende Methode: Verwenden Sie Testdaten verschiedener Zeiträume (OOT) zur Überprüfung während der Offline-Bewertung und beobachten Sie die Robustheit ihrer Leistung. Wenn die Testleistung relativ stabil ist, gibt es relativ mehr Grund zu der Annahme, dass die Online-Leistung auch gut ist.
2. Korrigierender Ursache-Wirkungs-Baum GBCT
1. Traditionell Der Kausalbaum
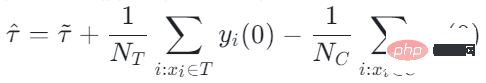
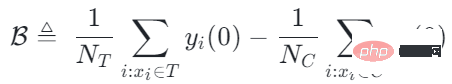
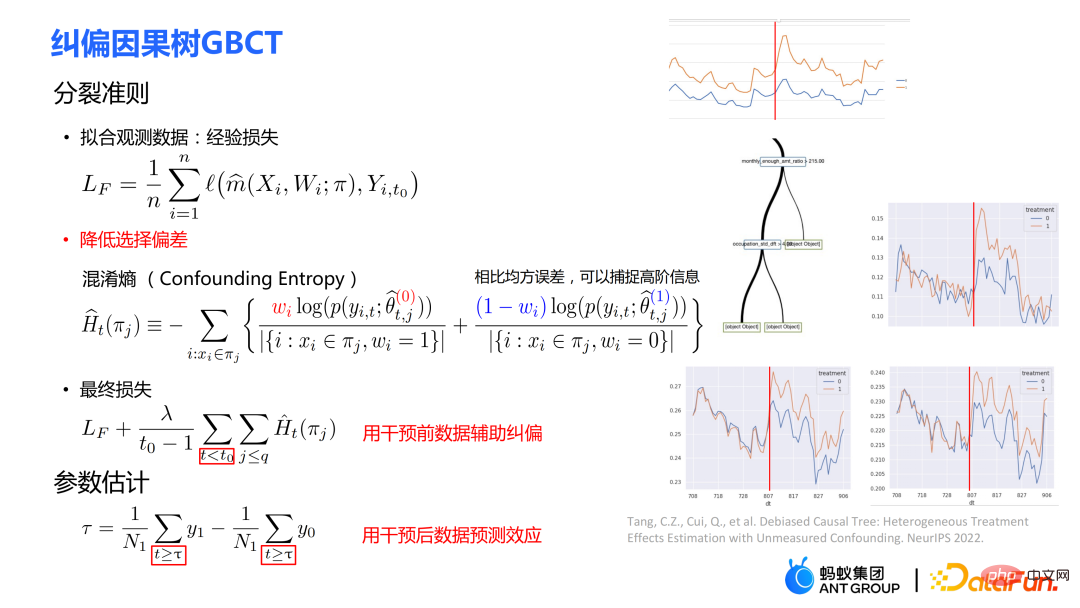
Die intuitive Bedeutung ist: im Experimentellen Verwenden Sie in der Kontrollgruppe das Modell der Kontrollgruppe zur Schätzung; in der Kontrollgruppe verwenden Sie das Modell der experimentellen Gruppe zur Schätzung, sodass die Verteilungen der experimentellen Gruppe möglichst nahe beieinander liegen Gruppe und Kontrollgruppe sind möglichst konsistent. Die Nutzung der Verwirrungsentropie ist einer der Hauptbeiträge unserer Arbeit.
② Parameterschätzung

3. Kausale Datenfusion

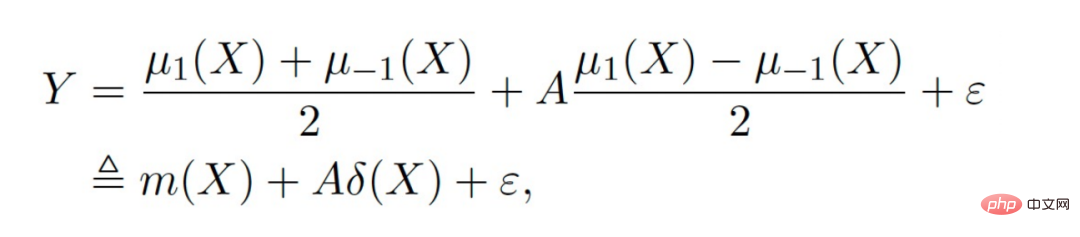
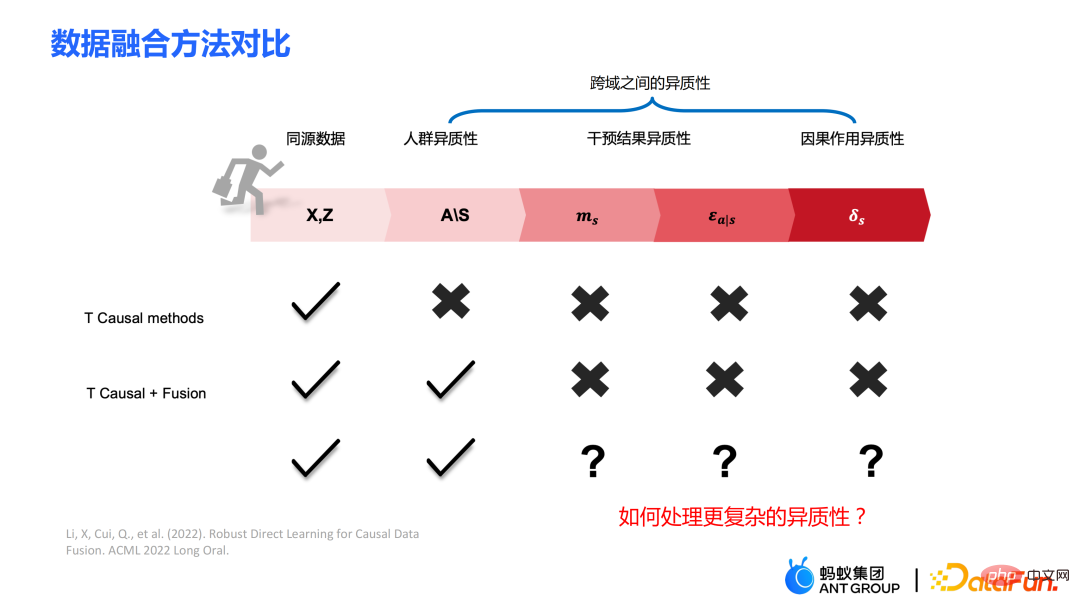
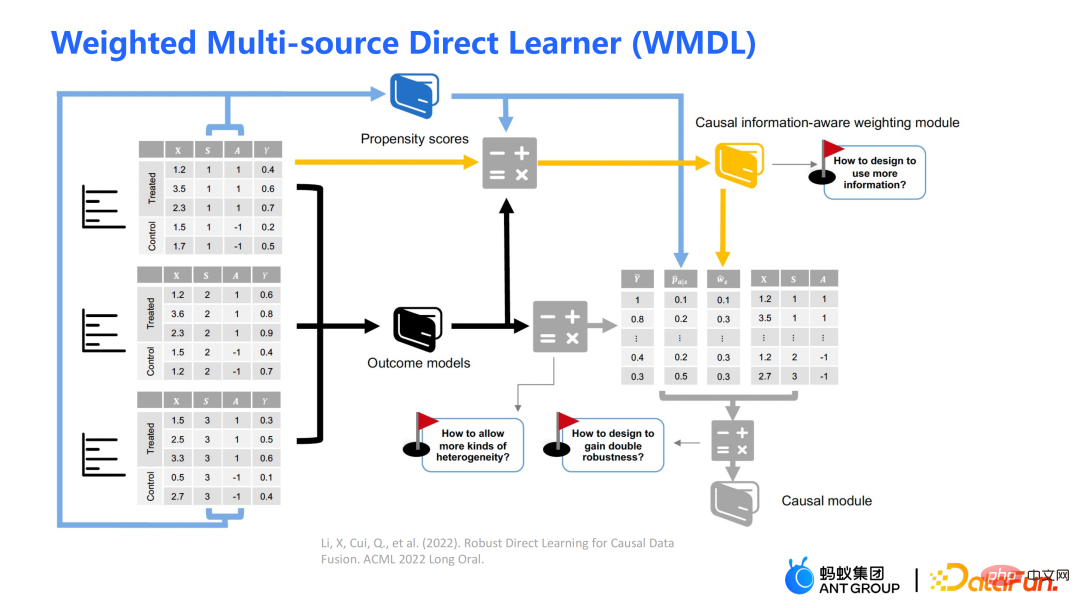
Der linke Teil geht davon aus, dass die kausalen Effekte zwischen mehreren Domänen gleich sind , aber seine Ergebnisse können heterogen sein; der rechte Teil geht davon aus, dass die kausalen Wirkungen zwischen den einzelnen Domänen unterschiedlich sind, das heißt, zwischen verschiedenen Domänen sind auch ihre kausalen Wirkungen unterschiedlich, selbst wenn ihre Kovariaten gleich sind. 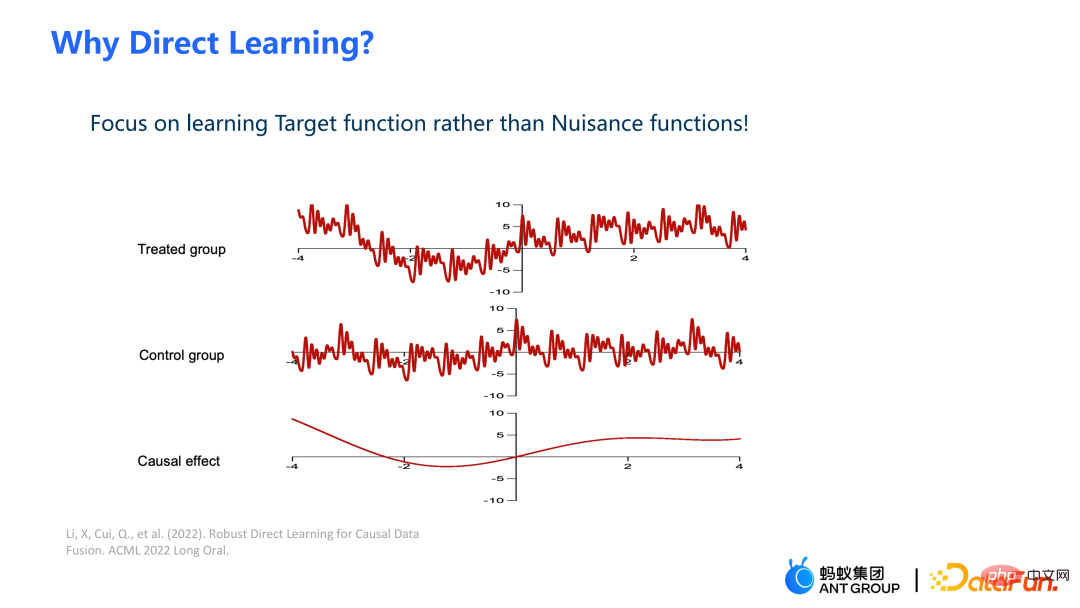
 ist das kausale informationsbewusste Gewichtungsmodul, das später erwähnt wird. Es stellt einen wesentlichen Beitrag unserer Arbeit dar. Der Nenner ähnelt dem Neigungswert in der doppelt robusten Methode, wird aber auch in diesem Arbeitsbereich berücksichtigt Information. Wenn die kausalen Effekte zwischen verschiedenen Domänen unterschiedlich sind, werden auch die Indikatorinformationen der Domäne berücksichtigt.
ist das kausale informationsbewusste Gewichtungsmodul, das später erwähnt wird. Es stellt einen wesentlichen Beitrag unserer Arbeit dar. Der Nenner ähnelt dem Neigungswert in der doppelt robusten Methode, wird aber auch in diesem Arbeitsbereich berücksichtigt Information. Wenn die kausalen Effekte zwischen verschiedenen Domänen unterschiedlich sind, werden auch die Indikatorinformationen der Domäne berücksichtigt. 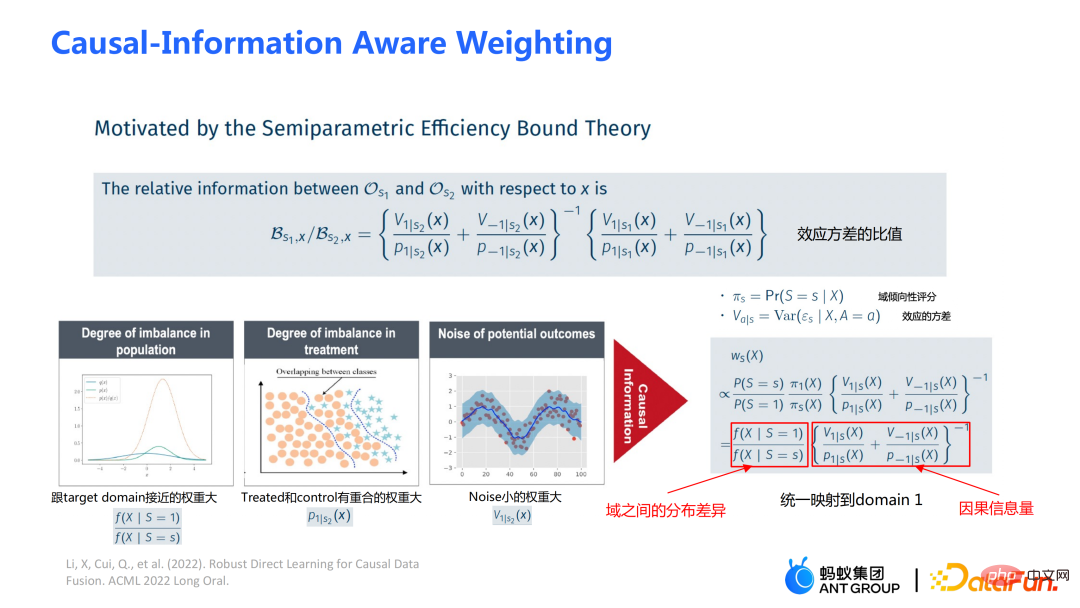 ①
① 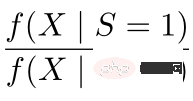 ist ein kausales Informationsmodul. Die drei Bilder auf der linken Seite können zum Verständnis dienen: Wenn der Verteilungsunterschied zwischen der Quelldomäne und der Zieldomäne groß ist, werden Proben bevorzugt, die näher an der Zieldomäne liegen ② Durch das Design der Neigungsbewertungsfunktion auf dem Nenner wird den überlappenden Stichproben in der Versuchsgruppe und der Kontrollgruppe ein größeres Gewicht gegeben.
ist ein kausales Informationsmodul. Die drei Bilder auf der linken Seite können zum Verständnis dienen: Wenn der Verteilungsunterschied zwischen der Quelldomäne und der Zieldomäne groß ist, werden Proben bevorzugt, die näher an der Zieldomäne liegen ② Durch das Design der Neigungsbewertungsfunktion auf dem Nenner wird den überlappenden Stichproben in der Versuchsgruppe und der Kontrollgruppe ein größeres Gewicht gegeben. 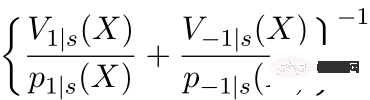 ③ Durch V wird das Rauschen in den Daten charakterisiert. Da das Rauschen im Nenner liegt, erhalten Proben mit weniger Rauschen größere Gewichte.
③ Durch V wird das Rauschen in den Daten charakterisiert. Da das Rauschen im Nenner liegt, erhalten Proben mit weniger Rauschen größere Gewichte. 
5. Frage- und Antwortsitzung
F1: Was sind die Gemeinsamkeiten und Unterschiede zwischen der GBCT-Korrektur und der Doppeldifferenzmethode (DID)?
F2: GBCT schneidet bei unbeobachteten Störvariablen besser ab. Gibt es eine intuitivere Erklärung?
F3: Haben Sie GBCT mit Double Machine Learning (DML) verglichen?
F4: Ein ähnliches Problem, das im Geschäftsleben auftreten kann, besteht darin, dass es offline zu Auswahlverzerrungen kommen kann. Allerdings kann sich die Online-Voreingenommenheit etwas von der Offline-Voreingenommenheit unterscheiden. Wenn die Effektbewertung offline durchgeführt wird, gibt es derzeit möglicherweise keine Möglichkeit, den Offline-Effekt sehr genau abzuschätzen.
Das obige ist der detaillierte Inhalt vonWie können Daten für kausale Schlussfolgerungen besser genutzt werden?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1379
1379
 52
52
 In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In den Bereichen maschinelles Lernen und Datenwissenschaft stand die Interpretierbarkeit von Modellen schon immer im Fokus von Forschern und Praktikern. Mit der weit verbreiteten Anwendung komplexer Modelle wie Deep Learning und Ensemble-Methoden ist das Verständnis des Entscheidungsprozesses des Modells besonders wichtig geworden. Explainable AI|XAI trägt dazu bei, Vertrauen in maschinelle Lernmodelle aufzubauen, indem es die Transparenz des Modells erhöht. Eine Verbesserung der Modelltransparenz kann durch Methoden wie den weit verbreiteten Einsatz mehrerer komplexer Modelle sowie der Entscheidungsprozesse zur Erläuterung der Modelle erreicht werden. Zu diesen Methoden gehören die Analyse der Merkmalsbedeutung, die Schätzung des Modellvorhersageintervalls, lokale Interpretierbarkeitsalgorithmen usw. Die Merkmalswichtigkeitsanalyse kann den Entscheidungsprozess des Modells erklären, indem sie den Grad des Einflusses des Modells auf die Eingabemerkmale bewertet. Schätzung des Modellvorhersageintervalls
 Identifizieren Sie Über- und Unteranpassung anhand von Lernkurven
Apr 29, 2024 pm 06:50 PM
Identifizieren Sie Über- und Unteranpassung anhand von Lernkurven
Apr 29, 2024 pm 06:50 PM
In diesem Artikel wird vorgestellt, wie Überanpassung und Unteranpassung in Modellen für maschinelles Lernen mithilfe von Lernkurven effektiv identifiziert werden können. Unteranpassung und Überanpassung 1. Überanpassung Wenn ein Modell mit den Daten übertrainiert ist, sodass es daraus Rauschen lernt, spricht man von einer Überanpassung des Modells. Ein überangepasstes Modell lernt jedes Beispiel so perfekt, dass es ein unsichtbares/neues Beispiel falsch klassifiziert. Für ein überangepasstes Modell erhalten wir einen perfekten/nahezu perfekten Trainingssatzwert und einen schrecklichen Validierungssatz-/Testwert. Leicht geändert: „Ursache der Überanpassung: Verwenden Sie ein komplexes Modell, um ein einfaches Problem zu lösen und Rauschen aus den Daten zu extrahieren. Weil ein kleiner Datensatz als Trainingssatz möglicherweise nicht die korrekte Darstellung aller Daten darstellt. 2. Unteranpassung Heru.“
 Transparent! Eine ausführliche Analyse der Prinzipien der wichtigsten Modelle des maschinellen Lernens!
Apr 12, 2024 pm 05:55 PM
Transparent! Eine ausführliche Analyse der Prinzipien der wichtigsten Modelle des maschinellen Lernens!
Apr 12, 2024 pm 05:55 PM
Laienhaft ausgedrückt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Eingabedaten einer vorhergesagten Ausgabe zuordnet. Genauer gesagt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Modellparameter anpasst, indem sie aus Trainingsdaten lernt, um den Fehler zwischen der vorhergesagten Ausgabe und der wahren Bezeichnung zu minimieren. Beim maschinellen Lernen gibt es viele Modelle, z. B. logistische Regressionsmodelle, Entscheidungsbaummodelle, Support-Vektor-Maschinenmodelle usw. Jedes Modell verfügt über seine anwendbaren Datentypen und Problemtypen. Gleichzeitig gibt es viele Gemeinsamkeiten zwischen verschiedenen Modellen oder es gibt einen verborgenen Weg für die Modellentwicklung. Am Beispiel des konnektionistischen Perzeptrons können wir es durch Erhöhen der Anzahl verborgener Schichten des Perzeptrons in ein tiefes neuronales Netzwerk umwandeln. Wenn dem Perzeptron eine Kernelfunktion hinzugefügt wird, kann es in eine SVM umgewandelt werden. Dieses hier
 Die Entwicklung der künstlichen Intelligenz in der Weltraumforschung und der Siedlungstechnik
Apr 29, 2024 pm 03:25 PM
Die Entwicklung der künstlichen Intelligenz in der Weltraumforschung und der Siedlungstechnik
Apr 29, 2024 pm 03:25 PM
In den 1950er Jahren wurde die künstliche Intelligenz (KI) geboren. Damals entdeckten Forscher, dass Maschinen menschenähnliche Aufgaben wie das Denken ausführen können. Später, in den 1960er Jahren, finanzierte das US-Verteidigungsministerium künstliche Intelligenz und richtete Labore für die weitere Entwicklung ein. Forscher finden Anwendungen für künstliche Intelligenz in vielen Bereichen, etwa bei der Erforschung des Weltraums und beim Überleben in extremen Umgebungen. Unter Weltraumforschung versteht man die Erforschung des Universums, das das gesamte Universum außerhalb der Erde umfasst. Der Weltraum wird als extreme Umgebung eingestuft, da sich seine Bedingungen von denen auf der Erde unterscheiden. Um im Weltraum zu überleben, müssen viele Faktoren berücksichtigt und Vorkehrungen getroffen werden. Wissenschaftler und Forscher glauben, dass die Erforschung des Weltraums und das Verständnis des aktuellen Zustands aller Dinge dazu beitragen können, die Funktionsweise des Universums zu verstehen und sich auf mögliche Umweltkrisen vorzubereiten
 Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Zu den häufigsten Herausforderungen, mit denen Algorithmen für maschinelles Lernen in C++ konfrontiert sind, gehören Speicherverwaltung, Multithreading, Leistungsoptimierung und Wartbarkeit. Zu den Lösungen gehören die Verwendung intelligenter Zeiger, moderner Threading-Bibliotheken, SIMD-Anweisungen und Bibliotheken von Drittanbietern sowie die Einhaltung von Codierungsstilrichtlinien und die Verwendung von Automatisierungstools. Praktische Fälle zeigen, wie man die Eigen-Bibliothek nutzt, um lineare Regressionsalgorithmen zu implementieren, den Speicher effektiv zu verwalten und leistungsstarke Matrixoperationen zu nutzen.
 Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Übersetzer |. Rezensiert von Li Rui |. Chonglou Modelle für künstliche Intelligenz (KI) und maschinelles Lernen (ML) werden heutzutage immer komplexer, und die von diesen Modellen erzeugten Ergebnisse sind eine Blackbox, die den Stakeholdern nicht erklärt werden kann. Explainable AI (XAI) zielt darauf ab, dieses Problem zu lösen, indem es Stakeholdern ermöglicht, die Funktionsweise dieser Modelle zu verstehen, sicherzustellen, dass sie verstehen, wie diese Modelle tatsächlich Entscheidungen treffen, und Transparenz in KI-Systemen, Vertrauen und Verantwortlichkeit zur Lösung dieses Problems gewährleistet. In diesem Artikel werden verschiedene Techniken der erklärbaren künstlichen Intelligenz (XAI) untersucht, um ihre zugrunde liegenden Prinzipien zu veranschaulichen. Mehrere Gründe, warum erklärbare KI von entscheidender Bedeutung ist. Vertrauen und Transparenz: Damit KI-Systeme allgemein akzeptiert und vertrauenswürdig sind, müssen Benutzer verstehen, wie Entscheidungen getroffen werden
 Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Maschinelles Lernen ist ein wichtiger Zweig der künstlichen Intelligenz, der Computern die Möglichkeit gibt, aus Daten zu lernen und ihre Fähigkeiten zu verbessern, ohne explizit programmiert zu werden. Maschinelles Lernen hat ein breites Anwendungsspektrum in verschiedenen Bereichen, von der Bilderkennung und der Verarbeitung natürlicher Sprache bis hin zu Empfehlungssystemen und Betrugserkennung, und es verändert unsere Lebensweise. Im Bereich des maschinellen Lernens gibt es viele verschiedene Methoden und Theorien, von denen die fünf einflussreichsten Methoden als „Fünf Schulen des maschinellen Lernens“ bezeichnet werden. Die fünf Hauptschulen sind die symbolische Schule, die konnektionistische Schule, die evolutionäre Schule, die Bayes'sche Schule und die Analogieschule. 1. Der Symbolismus, auch Symbolismus genannt, betont die Verwendung von Symbolen zum logischen Denken und zum Ausdruck von Wissen. Diese Denkrichtung glaubt, dass Lernen ein Prozess der umgekehrten Schlussfolgerung durch das Vorhandene ist
 Ist Flash Attention stabil? Meta und Harvard stellten fest, dass die Gewichtsabweichungen ihrer Modelle um Größenordnungen schwankten
May 30, 2024 pm 01:24 PM
Ist Flash Attention stabil? Meta und Harvard stellten fest, dass die Gewichtsabweichungen ihrer Modelle um Größenordnungen schwankten
May 30, 2024 pm 01:24 PM
MetaFAIR hat sich mit Harvard zusammengetan, um einen neuen Forschungsrahmen zur Optimierung der Datenverzerrung bereitzustellen, die bei der Durchführung groß angelegten maschinellen Lernens entsteht. Es ist bekannt, dass das Training großer Sprachmodelle oft Monate dauert und Hunderte oder sogar Tausende von GPUs verwendet. Am Beispiel des Modells LLaMA270B erfordert das Training insgesamt 1.720.320 GPU-Stunden. Das Training großer Modelle stellt aufgrund des Umfangs und der Komplexität dieser Arbeitsbelastungen einzigartige systemische Herausforderungen dar. In letzter Zeit haben viele Institutionen über Instabilität im Trainingsprozess beim Training generativer SOTA-KI-Modelle berichtet. Diese treten normalerweise in Form von Verlustspitzen auf. Beim PaLM-Modell von Google kam es beispielsweise während des Trainingsprozesses zu Instabilitäten. Numerische Voreingenommenheit ist die Hauptursache für diese Trainingsungenauigkeit.



