Optimaler Transport und seine Anwendung auf Gerechtigkeit
Übersetzer |. Li Rui. Die Ursprünge der Theorie des optimalen Transports lassen sich bis ins Jahr 1781 zurückverfolgen, als der französische Wissenschaftler Gaspard Monge eine Methode untersuchte, angeblich „die Erde zu bewegen“ und Befestigungen für Napoleons Armee zu bauen. Insgesamt besteht beim optimalen Transport das Problem, wie alle Ressourcen (z. B. Eisenerz) von einer Reihe von Ursprüngen (Minen) zu einer Reihe von Zielen (Stahlwerken) transportiert werden können und gleichzeitig die Gesamtentfernung, die die Ressourcen zurücklegen müssen, minimiert wird. Mathematisch wollten die Forscher eine Funktion finden, die jeden Ursprung einem Ziel zuordnet und gleichzeitig die Gesamtentfernung zwischen dem Ursprung und dem entsprechenden Ziel minimiert. Trotz seiner harmlosen Beschreibung stagnierte der Fortschritt bei der ursprünglichen Konzeption des Problems, bekannt als Mungers Konzeption, fast 200 Jahre lang.
In den 1940er Jahren adaptierte der sowjetische Mathematiker Leonid Kantorowitsch die Formulierung des Problems in eine moderne Version, die heute als Monge Kantorows Theorie bekannt ist, was den ersten Schritt zu einer Lösung darstellte. Die Neuheit besteht darin, dass ein Teil des Eisenerzes aus derselben Mine an verschiedene Stahlwerke geliefert werden kann. Beispielsweise können 60 % des Eisenerzes aus einer Mine an ein Stahlwerk geliefert werden, während die restlichen 40 % des Eisenerzes aus der Mine an ein anderes Stahlwerk geliefert werden können. Mathematisch gesehen ist dies keine Funktion mehr, da derselbe Ursprung nun potenziell mehreren Zielen zugeordnet ist. Im Gegensatz dazu wird dies als Kopplung zwischen der Ursprungsverteilung und der Zielverteilung bezeichnet, wie in der Abbildung unten gezeigt. Wenn Sie eine Mine aus der blauen Verteilung (Ursprung) auswählen und sich vertikal entlang der Abbildung bewegen, wird angezeigt, wohin das Eisenerz geschickt wird Stahlwerke (Ziel).Als Teil dieser neuen Entwicklung führte Kantorivich ein wichtiges Konzept namens Wasserstein-Distanz ein. Ähnlich wie der Abstand zwischen zwei Punkten auf einer Karte misst die Wasserstein-Distanz (in Anlehnung an das ursprüngliche Szenario auch als Bulldozer-Distanz bekannt) den Abstand zwischen zwei Verteilungen, wie in diesem Fall der blauen und der magentafarbenen Verteilung. Wenn alle Eisenminen weit von allen Eisenwerken entfernt sind, ist der Wasserstein-Abstand zwischen der Verteilung (Standort) der Minen und der Verteilung der Stahlwerke groß. Trotz dieser neuen Verbesserungen ist immer noch unklar, ob es wirklich die beste Möglichkeit für den Transport von Eisenerzressourcen gibt, geschweige denn welche Methode. In den 1990er Jahren begann sich die Theorie schließlich rasch weiterzuentwickeln, da Verbesserungen in der mathematischen Analyse und Optimierung zu Teillösungen des Problems führten. Im 21. Jahrhundert begann sich der optimale Transport auch auf andere Bereiche wie die Teilchenphysik, die Fluiddynamik und sogar Statistik und maschinelles Lernen auszudehnen.
moderner optimaler Transport 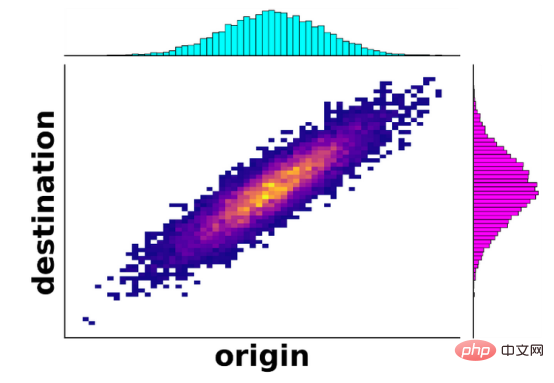
In diesem Fall beträgt der L-2-Abstand (oder die KL-Divergenz) zwischen der blauen und der magentafarbenen Verteilung ungefähr den Entspricht dem L-2-Abstand zwischen der blauen und der grünen Verteilung. Andererseits wird der Wasserstein-Abstand zwischen der Blau- und der Magenta-Verteilung viel kleiner sein als der Wasserstein-Abstand zwischen der Blau- und der Grün-Verteilung, da zwischen den Werten ein erheblicher Unterschied besteht (horizontale Trennung). Diese Eigenschaft des Wasserstein-Abstands macht ihn ideal für die Quantifizierung von Unterschieden zwischen Verteilungen, insbesondere von Unterschieden zwischen Datensätzen.
Erreichen Sie Fairness mit optimalem Transport 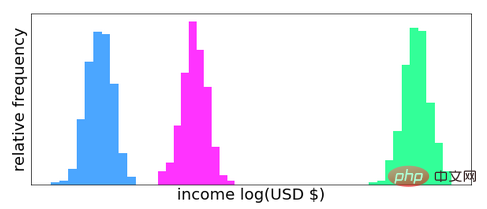
Die Optimierung des Versands kann dazu beitragen, diese Tendenz zu mildern und die Fairness auf zwei Arten zu verbessern. Die erste und einfachste Methode besteht darin, mithilfe der Wasserstein-Distanz zu bestimmen, ob im Datensatz eine potenzielle Verzerrung vorliegt. Beispielsweise kann man den Wasserstein-Abstand zwischen der Verteilung der für Frauen genehmigten Kreditbeträge und der Verteilung der für Männer genehmigten Kreditbeträge abschätzen. Ist der Wasserstein-Abstand sehr groß, also statistisch signifikant, kann ein potenzieller Bias vermutet werden. Diese Idee, zu testen, ob es einen Unterschied zwischen zwei Gruppen gibt, wird in der Statistik als Hypothesentest mit zwei Stichproben bezeichnet.
Alternativ kann der optimale Versand sogar verwendet werden, um Fairness im Modell durchzusetzen, wenn der zugrunde liegende Datensatz selbst verzerrt ist. Dies ist aus praktischer Sicht nützlich, da viele reale Datensätze ein gewisses Maß an Verzerrungen aufweisen und das Sammeln unvoreingenommener Daten sehr teuer, zeitaufwändig oder nicht durchführbar sein kann. Daher ist es praktischer, vorhandene Daten zu verwenden, egal wie unvollkommen sie sind, und zu versuchen, sicherzustellen, dass das Modell diese Verzerrung abmildert. Dies wird erreicht, indem eine Einschränkung im Modell erzwungen wird, die als starke demografische Parität bezeichnet wird und die Modellvorhersagen dazu zwingt, statistisch unabhängig von sensiblen Attributen zu sein. Ein Ansatz besteht darin, die Verteilung von Modellvorhersagen auf die Verteilung angepasster Vorhersagen abzubilden, die nicht von sensiblen Attributen abhängen. Allerdings verändert die Anpassung der Vorhersagen auch die Leistung und Genauigkeit des Modells, sodass ein Kompromiss zwischen der Modellleistung und dem Grad, in dem das Modell auf sensible Attribute angewiesen ist (d. h. Fairness), besteht.
Stellen Sie eine optimale Modellleistung sicher, indem Sie Vorhersagen so wenig wie möglich ändern und gleichzeitig sicherstellen, dass neue Vorhersagen unabhängig von sensiblen Attributen sind, was zu einem optimalen Versand führt. Die von diesem angepassten Modell vorhergesagte neue Verteilung wird Wasserstein-Schwerpunkt genannt und war im letzten Jahrzehnt Gegenstand umfangreicher Forschung. Der Wasserstein-Schwerpunkt ähnelt dem Mittelwert einer Wahrscheinlichkeitsverteilung darin, dass er den Gesamtabstand von sich selbst zu allen anderen Verteilungen minimiert. Das Bild unten zeigt drei Verteilungen (grün, blau und magenta) zusammen mit ihren Wasserstein-Schwerpunkten (rot).
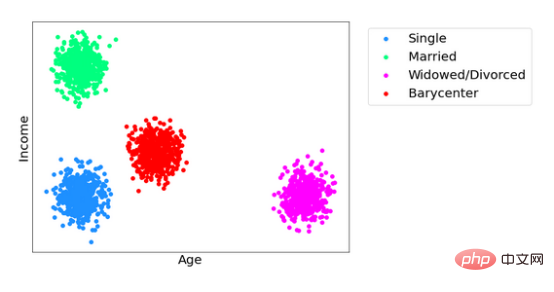
Nehmen wir im obigen Beispiel an, dass ein Modell erstellt wird, um das Alter und Einkommen einer Person auf der Grundlage eines Datensatzes vorherzusagen, der ein sensibles Attribut (z. B. Familienstand) enthält, das drei mögliche Werte annehmen kann: ledig (blau), verheiratet (grün) und verwitwet/geschieden (magenta). Das Streudiagramm zeigt die Verteilung der Modellvorhersagen für jeden unterschiedlichen Wert. Wenn Sie diese Werte jedoch so anpassen möchten, dass die Vorhersagen des neuen Modells den Familienstand einer Person nicht berücksichtigen, kann jede dieser Verteilungen mithilfe optimaler Transportmittel auf den Schwerpunkt in Rot abgebildet werden. Da alle Werte der gleichen Verteilung entsprechen, kann man den Familienstand einer Person nicht mehr anhand von Einkommen und Alter beurteilen oder umgekehrt. Der Schwerpunkt bewahrt die Wiedergabetreue des Modells so weit wie möglich.
Die zunehmende Allgegenwärtigkeit von Daten und Modellen des maschinellen Lernens, die bei der Entscheidungsfindung in Wirtschaft und Regierung eingesetzt werden, hat zur Entstehung neuer sozialer und ethischer Fragen darüber geführt, wie die faire Anwendung dieser Modelle sichergestellt werden kann. Viele Datensätze enthalten aufgrund der Art ihrer Erhebung eine gewisse Verzerrung. Daher ist es wichtig, dass auf ihnen trainierte Modelle diese Verzerrung oder historische Diskriminierung nicht verschärfen. Optimaler Transport ist nur eine Möglichkeit, dieses in den letzten Jahren zunehmende Problem zu lösen. Heutzutage gibt es schnelle und effiziente Möglichkeiten, optimale Transportkarten und Entfernungen zu berechnen, sodass dieser Ansatz für moderne große Datenmengen geeignet ist. Da sich die Menschen zunehmend auf datenbasierte Modelle und Erkenntnisse verlassen, ist Fairness ein Kernthema der Datenwissenschaft und wird auch weiterhin ein zentrales Thema sein, und optimale Transportmöglichkeiten werden eine Schlüsselrolle bei der Erreichung dieses Ziels spielen.
Originaltitel: Optimal Transport and its Applications to Fairness, Autor: Terrence Alsup
Das obige ist der detaillierte Inhalt vonOptimaler Transport und seine Anwendung auf Gerechtigkeit. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1376
1376
 52
52
 Bytedance Cutting führt SVIP-Supermitgliedschaft ein: 499 Yuan für ein fortlaufendes Jahresabonnement, das eine Vielzahl von KI-Funktionen bietet
Jun 28, 2024 am 03:51 AM
Bytedance Cutting führt SVIP-Supermitgliedschaft ein: 499 Yuan für ein fortlaufendes Jahresabonnement, das eine Vielzahl von KI-Funktionen bietet
Jun 28, 2024 am 03:51 AM
Diese Seite berichtete am 27. Juni, dass Jianying eine von FaceMeng Technology, einer Tochtergesellschaft von ByteDance, entwickelte Videobearbeitungssoftware ist, die auf der Douyin-Plattform basiert und grundsätzlich kurze Videoinhalte für Benutzer der Plattform produziert Windows, MacOS und andere Betriebssysteme. Jianying kündigte offiziell die Aktualisierung seines Mitgliedschaftssystems an und führte ein neues SVIP ein, das eine Vielzahl von KI-Schwarztechnologien umfasst, wie z. B. intelligente Übersetzung, intelligente Hervorhebung, intelligente Verpackung, digitale menschliche Synthese usw. Preislich beträgt die monatliche Gebühr für das Clipping von SVIP 79 Yuan, die Jahresgebühr 599 Yuan (Hinweis auf dieser Website: entspricht 49,9 Yuan pro Monat), das fortlaufende Monatsabonnement beträgt 59 Yuan pro Monat und das fortlaufende Jahresabonnement beträgt 499 Yuan pro Jahr (entspricht 41,6 Yuan pro Monat). Darüber hinaus erklärte der Cut-Beamte auch, dass diejenigen, die den ursprünglichen VIP abonniert haben, das Benutzererlebnis verbessern sollen
 Kontexterweiterter KI-Codierungsassistent mit Rag und Sem-Rag
Jun 10, 2024 am 11:08 AM
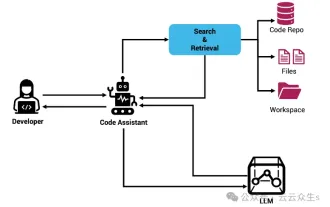
Kontexterweiterter KI-Codierungsassistent mit Rag und Sem-Rag
Jun 10, 2024 am 11:08 AM
Verbessern Sie die Produktivität, Effizienz und Genauigkeit der Entwickler, indem Sie eine abrufgestützte Generierung und ein semantisches Gedächtnis in KI-Codierungsassistenten integrieren. Übersetzt aus EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, Autor JanakiramMSV. Obwohl grundlegende KI-Programmierassistenten natürlich hilfreich sind, können sie oft nicht die relevantesten und korrektesten Codevorschläge liefern, da sie auf einem allgemeinen Verständnis der Softwaresprache und den gängigsten Mustern beim Schreiben von Software basieren. Der von diesen Coding-Assistenten generierte Code eignet sich zur Lösung der von ihnen zu lösenden Probleme, entspricht jedoch häufig nicht den Coding-Standards, -Konventionen und -Stilen der einzelnen Teams. Dabei entstehen häufig Vorschläge, die geändert oder verfeinert werden müssen, damit der Code in die Anwendung übernommen wird
 Sieben coole technische Interviewfragen für GenAI und LLM
Jun 07, 2024 am 10:06 AM
Sieben coole technische Interviewfragen für GenAI und LLM
Jun 07, 2024 am 10:06 AM
Um mehr über AIGC zu erfahren, besuchen Sie bitte: 51CTOAI.x Community https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou unterscheidet sich von der traditionellen Fragendatenbank, die überall im Internet zu sehen ist erfordert einen Blick über den Tellerrand hinaus. Large Language Models (LLMs) gewinnen in den Bereichen Datenwissenschaft, generative künstliche Intelligenz (GenAI) und künstliche Intelligenz zunehmend an Bedeutung. Diese komplexen Algorithmen verbessern die menschlichen Fähigkeiten, treiben Effizienz und Innovation in vielen Branchen voran und werden zum Schlüssel für Unternehmen, um wettbewerbsfähig zu bleiben. LLM hat ein breites Anwendungsspektrum und kann in Bereichen wie der Verarbeitung natürlicher Sprache, der Textgenerierung, der Spracherkennung und Empfehlungssystemen eingesetzt werden. Durch das Lernen aus großen Datenmengen ist LLM in der Lage, Text zu generieren
 Kann LLM durch Feinabstimmung wirklich neue Dinge lernen: Die Einführung neuen Wissens kann dazu führen, dass das Modell mehr Halluzinationen hervorruft
Jun 11, 2024 pm 03:57 PM
Kann LLM durch Feinabstimmung wirklich neue Dinge lernen: Die Einführung neuen Wissens kann dazu führen, dass das Modell mehr Halluzinationen hervorruft
Jun 11, 2024 pm 03:57 PM
Large Language Models (LLMs) werden auf riesigen Textdatenbanken trainiert und erwerben dort große Mengen an realem Wissen. Dieses Wissen wird in ihre Parameter eingebettet und kann dann bei Bedarf genutzt werden. Das Wissen über diese Modelle wird am Ende der Ausbildung „verdinglicht“. Am Ende des Vortrainings hört das Modell tatsächlich auf zu lernen. Richten Sie das Modell aus oder verfeinern Sie es, um zu erfahren, wie Sie dieses Wissen nutzen und natürlicher auf Benutzerfragen reagieren können. Aber manchmal reicht Modellwissen nicht aus, und obwohl das Modell über RAG auf externe Inhalte zugreifen kann, wird es als vorteilhaft angesehen, das Modell durch Feinabstimmung an neue Domänen anzupassen. Diese Feinabstimmung erfolgt mithilfe von Eingaben menschlicher Annotatoren oder anderer LLM-Kreationen, wobei das Modell auf zusätzliches Wissen aus der realen Welt trifft und dieses integriert
 Um ein neues wissenschaftliches und komplexes Frage-Antwort-Benchmark- und Bewertungssystem für große Modelle bereitzustellen, haben UNSW, Argonne, die University of Chicago und andere Institutionen gemeinsam das SciQAG-Framework eingeführt
Jul 25, 2024 am 06:42 AM
Um ein neues wissenschaftliches und komplexes Frage-Antwort-Benchmark- und Bewertungssystem für große Modelle bereitzustellen, haben UNSW, Argonne, die University of Chicago und andere Institutionen gemeinsam das SciQAG-Framework eingeführt
Jul 25, 2024 am 06:42 AM
Herausgeber | Der Frage-Antwort-Datensatz (QA) von ScienceAI spielt eine entscheidende Rolle bei der Förderung der Forschung zur Verarbeitung natürlicher Sprache (NLP). Hochwertige QS-Datensätze können nicht nur zur Feinabstimmung von Modellen verwendet werden, sondern auch effektiv die Fähigkeiten großer Sprachmodelle (LLMs) bewerten, insbesondere die Fähigkeit, wissenschaftliche Erkenntnisse zu verstehen und zu begründen. Obwohl es derzeit viele wissenschaftliche QS-Datensätze aus den Bereichen Medizin, Chemie, Biologie und anderen Bereichen gibt, weisen diese Datensätze immer noch einige Mängel auf. Erstens ist das Datenformular relativ einfach, die meisten davon sind Multiple-Choice-Fragen. Sie sind leicht auszuwerten, schränken jedoch den Antwortauswahlbereich des Modells ein und können die Fähigkeit des Modells zur Beantwortung wissenschaftlicher Fragen nicht vollständig testen. Im Gegensatz dazu offene Fragen und Antworten
 Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Maschinelles Lernen ist ein wichtiger Zweig der künstlichen Intelligenz, der Computern die Möglichkeit gibt, aus Daten zu lernen und ihre Fähigkeiten zu verbessern, ohne explizit programmiert zu werden. Maschinelles Lernen hat ein breites Anwendungsspektrum in verschiedenen Bereichen, von der Bilderkennung und der Verarbeitung natürlicher Sprache bis hin zu Empfehlungssystemen und Betrugserkennung, und es verändert unsere Lebensweise. Im Bereich des maschinellen Lernens gibt es viele verschiedene Methoden und Theorien, von denen die fünf einflussreichsten Methoden als „Fünf Schulen des maschinellen Lernens“ bezeichnet werden. Die fünf Hauptschulen sind die symbolische Schule, die konnektionistische Schule, die evolutionäre Schule, die Bayes'sche Schule und die Analogieschule. 1. Der Symbolismus, auch Symbolismus genannt, betont die Verwendung von Symbolen zum logischen Denken und zum Ausdruck von Wissen. Diese Denkrichtung glaubt, dass Lernen ein Prozess der umgekehrten Schlussfolgerung durch das Vorhandene ist
 SOTA Performance, eine multimodale KI-Methode zur Vorhersage der Protein-Ligand-Affinität in Xiamen, kombiniert erstmals molekulare Oberflächeninformationen
Jul 17, 2024 pm 06:37 PM
SOTA Performance, eine multimodale KI-Methode zur Vorhersage der Protein-Ligand-Affinität in Xiamen, kombiniert erstmals molekulare Oberflächeninformationen
Jul 17, 2024 pm 06:37 PM
Herausgeber |. KX Im Bereich der Arzneimittelforschung und -entwicklung ist die genaue und effektive Vorhersage der Bindungsaffinität von Proteinen und Liganden für das Arzneimittelscreening und die Arzneimitteloptimierung von entscheidender Bedeutung. Aktuelle Studien berücksichtigen jedoch nicht die wichtige Rolle molekularer Oberflächeninformationen bei Protein-Ligand-Wechselwirkungen. Auf dieser Grundlage schlugen Forscher der Universität Xiamen ein neuartiges Framework zur multimodalen Merkmalsextraktion (MFE) vor, das erstmals Informationen über Proteinoberfläche, 3D-Struktur und -Sequenz kombiniert und einen Kreuzaufmerksamkeitsmechanismus verwendet, um verschiedene Modalitäten zu vergleichen Ausrichtung. Experimentelle Ergebnisse zeigen, dass diese Methode bei der Vorhersage von Protein-Ligand-Bindungsaffinitäten Spitzenleistungen erbringt. Darüber hinaus belegen Ablationsstudien die Wirksamkeit und Notwendigkeit der Proteinoberflächeninformation und der multimodalen Merkmalsausrichtung innerhalb dieses Rahmens. Verwandte Forschungen beginnen mit „S
 GlobalFoundries erschließt Märkte wie KI und erwirbt die Galliumnitrid-Technologie von Tagore Technology und zugehörige Teams
Jul 15, 2024 pm 12:21 PM
GlobalFoundries erschließt Märkte wie KI und erwirbt die Galliumnitrid-Technologie von Tagore Technology und zugehörige Teams
Jul 15, 2024 pm 12:21 PM
Laut Nachrichten dieser Website vom 5. Juli veröffentlichte GlobalFoundries am 1. Juli dieses Jahres eine Pressemitteilung, in der die Übernahme der Power-Galliumnitrid (GaN)-Technologie und des Portfolios an geistigem Eigentum von Tagore Technology angekündigt wurde, in der Hoffnung, seinen Marktanteil in den Bereichen Automobile und Internet auszubauen Anwendungsbereiche für Rechenzentren mit künstlicher Intelligenz, um höhere Effizienz und bessere Leistung zu erforschen. Da sich Technologien wie generative künstliche Intelligenz (GenerativeAI) in der digitalen Welt weiterentwickeln, ist Galliumnitrid (GaN) zu einer Schlüssellösung für nachhaltiges und effizientes Energiemanagement, insbesondere in Rechenzentren, geworden. Auf dieser Website wurde die offizielle Ankündigung zitiert, dass sich das Ingenieurteam von Tagore Technology im Rahmen dieser Übernahme mit GF zusammenschließen wird, um die Galliumnitrid-Technologie weiterzuentwickeln. G




