
「In einem gewichteten gerichteten Graphen G=(V,E) ist das Gewicht jeder Kante eine reelle Zahl. Darüber hinaus ist auch ein Scheitelpunkt in V angegeben, der als Quelle bezeichnet wird.
Berechnen des Die Länge des kürzesten Weges von der Quelle zu allen anderen Eckpunkten ist das Problem des Single-Source-Shortest-Path (SSSP). Seit mehr als einem halben Jahrhundert arbeiten Forscher auf der ganzen Welt hart daran, dieses Problem zu lösen. Nun wurde dieses algorithmische Rätsel endlich von einem Forschungsteam der Fakultät für Informatik der Universität Kopenhagen erfolgreich gelöst.
Negatives Gewicht SSSP -Algorithmus: Schneller und effizienter Link: https://arxiv.org/abs/2203.03456
in ein Interview, sagte der Forscher Christian Wulff -nilsen das Ihre Lösung ist der erste SSSP-Kombinationsalgorithmus mit negativen Gewichten, der die seit mehr als 30 Jahren bestehende
Õ( n
n
W) Betriebszeitbeschränkung durchbricht.
Es gibt zwei klassische Algorithmen für SSSP: den Dijkstra-Algorithmus (Dijkstra-Algorithmus) und den Bellman-Ford-Algorithmus (Bellman-Ford-Algorithmus), die beide ihre eigenen Einschränkungen haben. Der Dijkstra-Algorithmus hat die kürzeste Operationszeit und kann eine nahezu lineare Zeit O(m
+n log n) erreichen, kann jedoch keine Kanten mit negativem Gewicht berechnen.
Der Bellman-Ford-Algorithmus kann negative Gewichtskanten berechnen, aber die Operationszeit ist zu lang und erreicht O(mn). Derzeit basieren die hochmodernen SSSP-Algorithmen zur Lösung negativ gewichteter Kanten auf komplexer kontinuierlicher Optimierung sowie dynamischen algebraischen und grafischen Algorithmen. Dies führt dazu, dass selbst wenn spätere Generationen von Wissenschaftlern den Algorithmus weiter optimieren, seine Berechnungszeit immer noch Õ(n(4/3) log W
) erfordert. Diese Rechenzeitbeschränkung besteht seit dreißig Jahren.Angesichts dieser Einschränkungen stellte Wulff-Nilsen zwei Fragen: 1) Kann der Betrieb des negativ gewichteten Kantenalgorithmus eine nahezu lineare Zeit erreichen?
2) Lässt sich das mit einfachen Werkzeugen erreichen?
Gibt es eine Methode, die sowohl Zeit als auch Qualität erfordert?
Sag es nicht, es existiert wirklich.
Der von Wulff-Nilsen vorgeschlagene Algorithmus ist ein Bildskalierungsalgorithmus, der durch den einfachen Bildzerlegungsalgorithmus Low Diameter Decomposition erweitert wird. Normalerweise wird dieser Zerlegungsalgorithmus nur für die Graphenzerlegung von nicht negativ gewichteten Kanten verwendet. Einer der Beiträge dieser Forschung besteht darin, ihn auf negativ gewichtete Kantenbilder anzuwenden, um den rekursiven SSSP-Skalierungsalgorithmus für negativ gewichtete Kanten zu stärken.
Der AbleitungsprozessWulff-Nilsen basiert auf dem Preisalgorithmus von Johnson. Schlagen Sie vor: Im Bild G
= (V, E, w) sei Φ
eine beliebige Funktion:V→Z
. Seiw(Φ) die Gewichtsfunktion: Definition: , : . Im Bild G = (V, E,w) und im Bild G' = (V, E,w'), wenn: 1) Bild Der kürzeste Abstand in G ist gleich dem kürzesten Abstand im Bild G' und umgekehrt; 2) G enthält nur dann negative Gewichtsringe, wenn G' negatives Gewicht enthält Ringe, dann ist das Bild G gleich dem Bild G'. Korollar 2.7 Betrachten Sie ein beliebiges Bild Der Zweck dieses Algorithmus besteht darin, alle Kantengewichte in GΦ bei der Berechnung der Preisfunktion Φ nicht negativ zu machen, vorausgesetzt, es gibt keinen negativen Gewichtszyklus. Dann können Sie den Dijkstra-Algorithmus auf Danach begann Wulff-Nilsen mit der Einführung seines Algorithmus-Frameworks. Zunächst geht Wulff-Nilsen davon aus, dass es einen Dijkstra-Algorithmus (G,s) gibt, der einen Graphen G ohne negative Gewichtskanten, Scheitelpunkte s∈ V, G eingibt s gibt den kürzesten Pfadbaum aus. Die Laufzeit beträgt O(m + n log n). Wenn G ein DAG (gerichteter azyklischer Graph) ist, berechnen Sie eine Preisfunktion Φ so dass #🎜🎜 ## 🎜🎜#Kanten mit nicht negativem Gewicht zu haben ist einfach: Führen Sie einfach eine Schleife über v1, ..., vn der Topologie durch und setzen Sie Das Ziel des Single-Source-Shortest-Path-Problems besteht darin, den kürzesten Pfad von einem gegebenen Startknoten zu allen anderen Knoten in zu finden das Netzwerk. Ein Netzwerk wird als Graph dargestellt, der aus Knoten und den Verbindungen zwischen ihnen, Kanten genannt, besteht. Jede Kante hat eine Richtung (dies kann beispielsweise zur Darstellung einer Einbahnstraße verwendet werden) und ein Gewicht, das stellt die Entlangfahrtkosten auf dieser Seite dar. Wenn alle Kantengewichte nicht negativ sind, kann das Problem mit dem klassischen Dijkstra-Algorithmus in nahezu linearer Zeit gelöst werden. Die neuen Ergebnisse lösen dieses Problem fast zeitgleich mit dem Dijkstra-Algorithmus, ermöglichen aber auch negative Kantengewichte. Danach erwähnte Wulff-Nilsen die beiden wichtigsten Algorithmen in Kombinationstools: ScaleDown und SPmain. ScaleDown-Algorithmus läuft in Stufen und verwendet in der letzten Stufe ElimNeg ( ) zur Berechnung der Preisfunktion 2. Wenn ElimNeg beendet wird, wird die Preisfunktion zurückgegeben Wenn der Algorithmus terminiert, dann gilt für alle Das bedeutet für alle Angenommen, die Theorie gilt durch Induktion für Daher durch Weil Daher können wir schließen, dass der Algorithmus nicht beendet wird, wenn Dies kann die Korrektheit des SPmain-Algorithmus beweisen. Zu diesem Zeitpunkt haben sich die beiden wichtigsten Algorithmen in Wulff-Nilsens SSSP-Lösung mit negativem Gewicht als wahr erwiesen. Der neue Algorithmus führt erfolgreich negative Gewichte ein und gewährleistet gleichzeitig eine nahezu lineare Zeit. Letztes Jahr gelang Wulff-Nilsen ein weiterer Durchbruch auf demselben Gebiet, nämlich wie man den kürzesten Weg in einem findet Netzwerk, das sich im Laufe der Zeit ändert. Seine Lösung eines aktuellen Rätsels baut auf dieser Arbeit auf. Er glaubt, dass die Lösung des SSSP-Problems den Weg für Algorithmen ebnen kann, die Elektrofahrzeugen nicht nur dabei helfen können, sofort die schnellste Route zu ihrem Ziel zu berechnen, sondern auch sicherzustellen, dass sie dies auf die energieeffizienteste Weise tun. Wulff-Nilsen erklärte: „Unser Algorithmus fügt negatives Gewicht hinzu, eine Dimension, die frühere Algorithmen nicht hatten. Ein praktisches Beispiel ist das Fahren in den Bergen mit der negativen Gewichtungsdimension, mit der das Navigationssystem Routen empfehlen kann.“ Viele bergab gelegene Straßen für Besitzer von Elektrofahrzeugen, damit Elektrofahrzeuge beim Bergabfahren aufgeladen werden können.“ der Finanzbranche. Er sagte: „Im Prinzip kann dieser Algorithmus verwendet werden, um Benutzer wie Zentralbanken frühzeitig zu warnen und Spekulanten zu warnen, die mit dem Kauf und Verkauf verschiedener Währungen spekulieren. Heutzutage nutzen viele Kriminelle Computer, um Verbrechen zu begehen, aber weil unser Algorithmus es ist.“ so schnell, dass es möglich sein könnte, Schwachstellen rechtzeitig zu überwachen und zu erkennen, bevor sie von Menschen ausgenutzt werden als 60 Jahre planen. Sie werden vielleicht auch überrascht sein, dass die Antwort auf das Rätsel so vielschichtige Bedeutungen hat. Vielleicht ist das der Reiz der Wissenschaft. 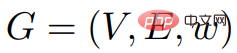 und eine Preisfunktion Φ. In u, v ∈ V,
und eine Preisfunktion Φ. In u, v ∈ V, 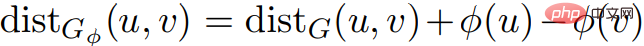 . Und in jedem Ring C,
. Und in jedem Ring C, 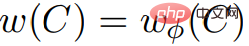 . Daher sind G und
. Daher sind G und 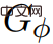 gleich. Wenn
gleich. Wenn 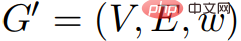
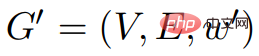 ,
,  , , dann sind G und G' gleich.
, , dann sind G und G' gleich. 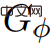 ausführen.
ausführen. 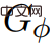 Φ(vi) so, dass alle eingehenden Kantengewichte gelten nicht negativ.
Φ(vi) so, dass alle eingehenden Kantengewichte gelten nicht negativ.  Φ
Φ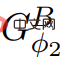 ψ′, let # 🎜🎜#Alle Kantenwerte sind nicht negativ; mit anderen Worten, weil , , also enthält keine negativen Gewichte.
ψ′, let # 🎜🎜#Alle Kantenwerte sind nicht negativ; mit anderen Worten, weil , , also enthält keine negativen Gewichte. 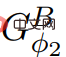
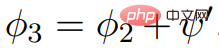 Das bedeutet, dass für alle die Bedingung erfüllt (weil
Das bedeutet, dass für alle die Bedingung erfüllt (weil 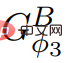 ). Dies beweist die Korrektheit der ScaleDown-Ausgabe.
). Dies beweist die Korrektheit der ScaleDown-Ausgabe. 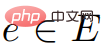 und
und 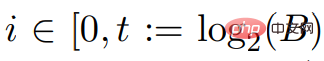 ,
, 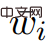 ist Punkte, und für alle
ist Punkte, und für alle 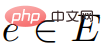 ,
, 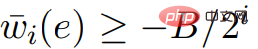 .
. 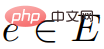 ,
, 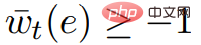 . Daher hat der Graph G* nicht negative Gewichte.
. Daher hat der Graph G* nicht negative Gewichte. 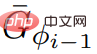 , Der Aufruf von ScaleDown
, Der Aufruf von ScaleDown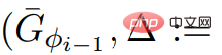
 in Zeile 5 des Algorithmus erfüllt die notwendigen Eingabeattribute.
in Zeile 5 des Algorithmus erfüllt die notwendigen Eingabeattribute. 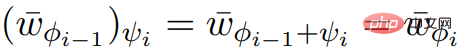 und ScaleDown Output , Sie können
und ScaleDown Output , Sie können 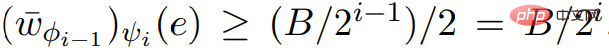 bekommen.
bekommen. 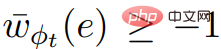 , Wenn C irgendein negatives Gewicht ist, klingeln Sie in
, Wenn C irgendein negatives Gewicht ist, klingeln Sie in 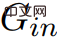 , da alle Werte von in
, da alle Werte von in  Vielfache von 2n und sind
Vielfache von 2n und sind 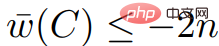 ; Wir wissen auch, dass
; Wir wissen auch, dass 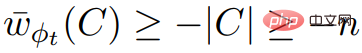 , , also
, , also 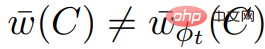 nicht mit Korollar 2.7 vereinbar ist.
nicht mit Korollar 2.7 vereinbar ist. 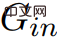 einen negativen Gewichtszyklus enthält.
einen negativen Gewichtszyklus enthält. 60 Jahre später ist die Suche nach Antworten mehr als nur ein Rätsel
Das obige ist der detaillierte Inhalt vonEin Puzzle von vor 60 Jahren! Forscher der Universität Kopenhagen lösen das Problem des „kürzesten Weges aus einer Hand'.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




