 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Globale Positionierungstechnologie basierend auf Merkmalspunkten beim autonomen Fahren mithilfe der Wanzi-Analyse
Globale Positionierungstechnologie basierend auf Merkmalspunkten beim autonomen Fahren mithilfe der Wanzi-Analyse
Globale Positionierungstechnologie basierend auf Merkmalspunkten beim autonomen Fahren mithilfe der Wanzi-Analyse
Im autonomen Fahren sind Wahrnehmung, Positionierung, Planung und Entscheidungsfindung sowie Steuerung die vier grundlegenden Systemmodule. Da der aktuelle Algorithmus keine absolute Intelligenz erreichen kann, ist noch viel Vorwissen erforderlich, um die Leistung und Robustheit des Moduls zu verbessern und so ein sicheres autonomes Fahren zu erreichen. Zu den hochpräzisen Karten gehört die Integration von Vorkenntnissen über Straßen und Umgebungen. Die genaue Positionierung anhand der Karte ist eine wichtige Grundlage zur Beurteilung der Fahrbedingungen und liefert eine starke Unterstützung für spätere Wahrnehmungs- und Planungsentscheidungen.
Zu den wichtigsten Datenquellen für die Positionierung gehören derzeit GPS, Lidar, Vision und Millimeterwellenradar. Obwohl es in der Branche derzeit keine ausreichend zuverlässige Positionierungslösung gibt, hat die Forschung in diesem Bereich nie aufgehört:
Sicherheit ist der wichtigste Indikator für unbemannte Fahrsysteme, daher die Implementierung Eine der meisten Funktionen ist die Kopplung von Daten aus mehreren Quellen und unterschiedlichen Algorithmusergebnissen. Keine Sensorlösung ist perfekt. Als weit verbreitete Lösung wird GPS RTK beispielsweise leicht durch Satellitenbedingungen, Wetterbedingungen und Datenübertragungsbedingungen beeinflusst und kann nicht in Tunneln, Innenräumen und dicht besiedelten Gebieten mit hohen Gebäuden eingesetzt werden . Darüber hinaus bietet Lidar zwar die Vorteile eines geringen Rechenaufwands, liefert Tiefeninformationen und wird nicht durch die Beleuchtung beeinflusst, die Informationen sind jedoch spärlich, die Kosten sind immer noch sehr hoch und es ist noch nicht in der Lage, große Mengen an Fahrzeugen zusammenzubauen. Im Vergleich dazu werden die von Kameras bereitgestellten visuellen Informationen zwar von Licht und Wetter beeinflusst, sind jedoch kostengünstig und inhaltsreich. Sie sind die Hauptdatenquelle für aktuelle Lösungen für das assistierte Fahren und bieten auch großes Potenzial für die Kartenpositionierung.
Da die Kernideen der gängigen visuellen Positionierungsalgorithmen dieselben sind, stellt dieser Artikel nur den in der Praxis am häufigsten verwendeten globalen Positionierungsalgorithmus basierend auf Merkmalspunkten aus der Perspektive einer Reihe wichtiger Algorithmus-Framework-Komponenten vor, nämlich in das Kartenkoordinatensystem zur Position. In diesem Artikel wird auf die damit verbundene Optimierung und Ableitung der geometrischen Zwangsformel verzichtet, um den Schülern eine makroökonomische Einführung in Positionierungsalgorithmen zu geben. Weitere Informationen finden Sie in der entsprechenden Literatur und in Büchern.
Basierend auf dem globalen Positionierungsalgorithmus von Merkmalspunkten
Visuelle globale Positionierung bezieht sich auf das Finden der Pose (Pose) der Kamera mit 6 Freiheitsgraden (DoF) im Kartenkoordinatensystem basierend auf dem aktuellen Bild ist, (x, y, z)-Koordinaten und Winkelauslenkungen (Gieren, Nicken, Rollen) um die drei Koordinatenachsen. Derzeit kann es hauptsächlich in 3D-strukturbasierte Methoden, 2D-bildbasierte Methoden, sequenzbildbasierte Methoden und Deep-Learning-basierte Methoden klassifiziert werden. Unter diesen sind auf Deep Learning basierende Methoden End-to-End-Methoden, während andere mehrstufige (mehrstufige) Nicht-End-to-End-Methoden unterschiedliche Prozesse haben, die Algorithmusideen jedoch größtenteils wie in Abb. 1 dargestellt sind Darstellung:

Abbildung 1: Berechnen Sie basierend auf dem Abfragebild die 2D-3D-Transformationsmatrix und lösen Sie die Kameraposition.
Passen Sie basierend auf der erstellten Karte die ähnlichste Kartenteilmenge in der Geschichte an (Bild/Punktwolke/Feature-Punkt), basierend auf dem wahren historischen Posenwert und dem wahren Wert der Feature-Punktkoordinate, der von der übereinstimmenden Kartenteilmenge bereitgestellt wird, berechnen Sie die Transformationsmatrix zwischen Punktpaaren und lösen Sie die aktuelle Kamerapose.
Der Kern umfasst also vier Aspekte: Bildbeschreibung, Zuordnungsabfrage, Merkmalsabgleich und Posenberechnung. Dabei handelt es sich nur um eine Makroklassifizierung auf technischer Ebene. Das tatsächliche Algorithmus-Framework wird möglicherweise nicht unbedingt in dieser Reihenfolge ausgeführt, und Wissenschaftler konzentrieren sich in ihrer Forschung hauptsächlich auf die Verbesserung dieser Technologien. Insgesamt ist die auf Merkmalspunkten basierende Bildbeschreibung grundsätzlich ausgereift und hat weniger Entwicklung. Da es sich bei der Posenberechnung um ein Optimierungsproblem handelt, das auf geometrischen Einschränkungen basiert, ist die Methode relativ fest. Im Gegensatz dazu gibt es viele verbesserte Techniken bei der Zuordnung von Abfragen und dem Feature-Matching. Abhängig von der Datenquelle können Zuordnungsabfrage und -abgleich 2D-2D, 2D-3D oder 3D-3D sein. 2D-Bilder werden von Kameras aufgenommen und 3D-Punktwolken können von Fernglaskameras oder RGB-D-Kameras erzeugt werden, die für Tiefe sorgen.
Feature Point Extraction
Das 2D-Bild selbst ist eine Matrix aus Helligkeit und Farbe. Es reagiert sehr empfindlich auf Betrachtungswinkel, Beleuchtung, Farbtonänderungen usw. und ist sehr schwierig direkt zu verwenden. Daher werden im Allgemeinen repräsentative Punkte für relevante Berechnungen verwendet. Die Menschen hoffen, dass solche Punkte die Vorteile von Rotation, Translation, Skalierung, Beleuchtungsinvarianz usw. haben. Diese Punkte werden als Merkmalspunkte des Bildes bezeichnet, einschließlich Schlüsselpunkten und Deskriptoren. Schlüsselpunkte drücken die Position von Merkmalspunkten aus, während Deskriptoren die visuellen Eigenschaften von Merkmalspunkten beschreiben, meist in Vektorform. Im Allgemeinen zählen Deskriptoren hauptsächlich Graustufen-/Farbverlaufsänderungen um Schlüsselpunkte in einem bestimmten Muster. Für einen robusten Deskriptor sollte der Abstand (Distance) des Deskriptors desselben Merkmalspunkts in verschiedenen Situationen in verschiedenen Bildern kleiner sein.
Deskriptoren sind im Allgemeinen handgefertigte Funktionen. Zu den klassischen Beschreibungen gehören HOG (Histogram of Oriented Gradients) [1], SIFT (Scale-invariant Feature Transform) [2], SURF (Speeded Up Robust Features) [3], AKAZE (Accelerated KAZE) [4] usw.
Um die Echtzeitanforderungen zu erfüllen, wurden einige binäre Musterdeskriptoren mit schnellerer Berechnungsgeschwindigkeit entwickelt, wie z. B. LBP (Local Binary Patterns) [5], BRIEF (Binary Robust Independent Elementary Features) und ORB (Oriented). SCHNELLER und gedrehter KURZ)[6], BRISK(Binärer robuster invarianter skalierbarer Schlüsselpunkt)[7], FREAK(Schneller Retina-Schlüsselpunkt)[8] usw.
Bevor Deep Learning populär wurde, waren diese handgefertigten Funktionen führend in der gesamten Computational Vision-Branche. Bis heute werden diese Funktionen häufig in Szenarien verwendet, in denen es an gekennzeichneten Daten mangelt und die viele Einschränkungen aufweisen. Im Folgenden finden Sie eine kurze Einführung in zwei häufig verwendete Deskriptoren.
SIFT
SIFT-Deskriptor kann als eine der einflussreichsten Technologien in der Lebenslaufwelt angesehen werden. Auf der Ebene der Schlüsselpunkterkennung wird die Differenz-Gauß-Methode (DoG) hauptsächlich verwendet, um Extrempunkte im Raum mit mehreren Maßstäben als Schlüsselpunkte zu erkennen. Babaud et al. [9] haben bewiesen, dass die Gaußsche Glättung der einzige verwendbare mehrskalige räumliche Glättungsfilterkern ist, der ausreichende theoretische Unterstützung für verwandte Methoden bietet.
Warum kann eine solche Methode wichtige Merkmalspunkte finden?
Weil der Gaußsche Kern das Bild durch Unschärfe auf unterschiedliche Skalenräume skalieren kann und sich die Werte glatter Bereiche mit kleinen Farbverläufen in unterschiedlichen Skalenräumen ändern Die Lücke ist kleiner. Im Gegenteil, die Unterschiede sind in Bereichen wie Kanten, Punkten, Ecken und Texturen größer. Auf diese Weise können durch Differenzierung zwischen Bildern benachbarter Maßstäbe schließlich die Extrempunkte des Mehrmaßstabsraums berechnet werden. Allerdings liegen unterschiedliche Bilddetails naturgemäß in unterschiedlichen Maßstäben vor. Beispielsweise kann bei einem Porträt das Gesicht nach einer kleinen Unschärfe in einem Stück geglättet werden, während die Ecken des Rahmens möglicherweise eine Glättung in größerem Maßstab erfordern, um lokale „Extremwerte“ widerzuspiegeln.
Daher werden die Bilder, wie in Abb. 2 gezeigt, zunächst mithilfe der Bildpyramide gruppiert (Oktave), und in jeder Gruppe werden Gaußsche Kerne unterschiedlicher Maßstäbe verwendet, um eine Reihe von Schichten zu bilden. Diese Methode ist besser als die einfache Verwendung mehr Skalen von Gaußschen Kerneln und kann mehr Merkmalspunkte erkennen. Es ist zu beachten, dass SIFT zwar DoG zur Schlüsselpunkterkennung verwendet, andere Erkennungsmethoden jedoch ebenfalls möglich sind und keinen Einfluss auf die Einrichtung von SIFT-Deskriptoren haben.
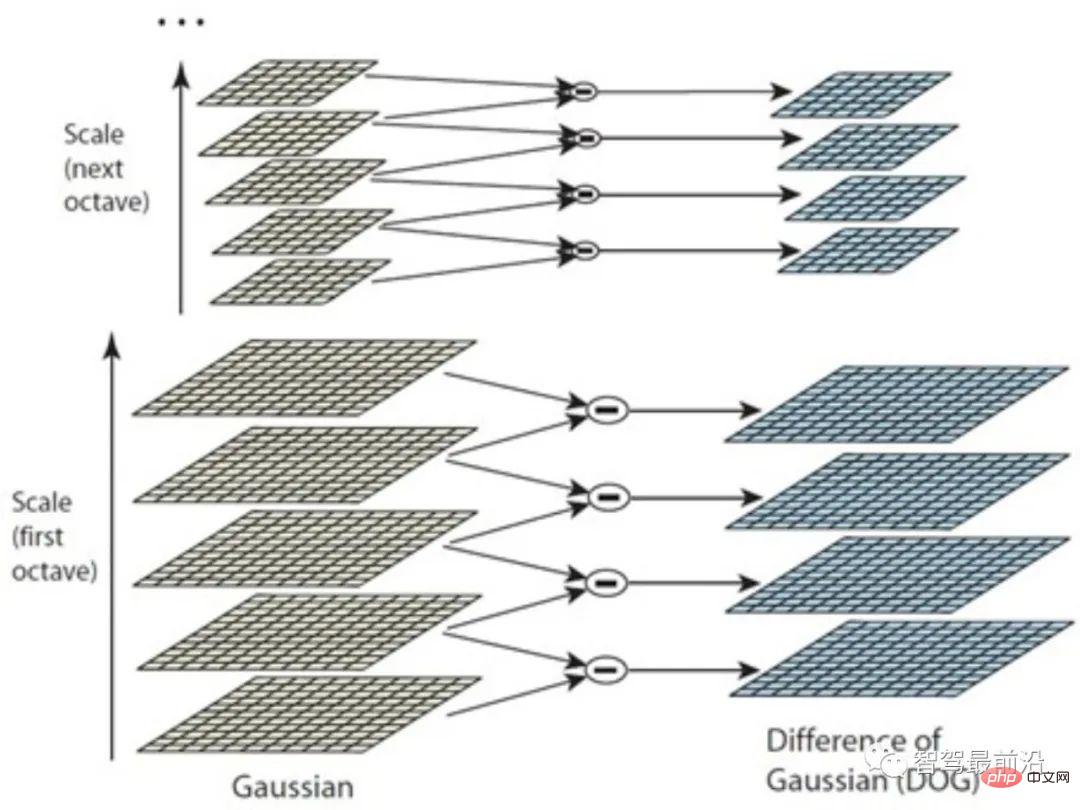
Abbildung 2: Gaußsche Differenzmethode
SIFT-Feature-Point-Deskriptor kann als einfache statistische Version von HOG verstanden werden. Wie in Abb. 3 dargestellt, wird mit dem erkannten Schlüsselpunkt als Mittelpunkt ein umgebender 16 × 16-Bereich ausgewählt und der Bereich in vier 4 × 4-Patches neu organisiert. Für jeden Block wird ein 8-Bins-Histogramm verwendet, um den Gradienten zu zählen. Die Richtung des Gradienten bestimmt, in welches Bin er fällt, und das Modul des Gradienten bestimmt die Größe des Werts. Um die Skalenkonsistenz sicherzustellen, muss die Gradientengröße normalisiert werden. Um die Rotationsinvarianz sicherzustellen, wird eine Hauptrichtung basierend auf allen Gradienten im 16 × 16-Bereich berechnet und alle Gradienten werden entsprechend der Hauptrichtung gedreht. Das Ergebnis ist ein 4 × 4 × 8 128-dimensionaler Vektor.
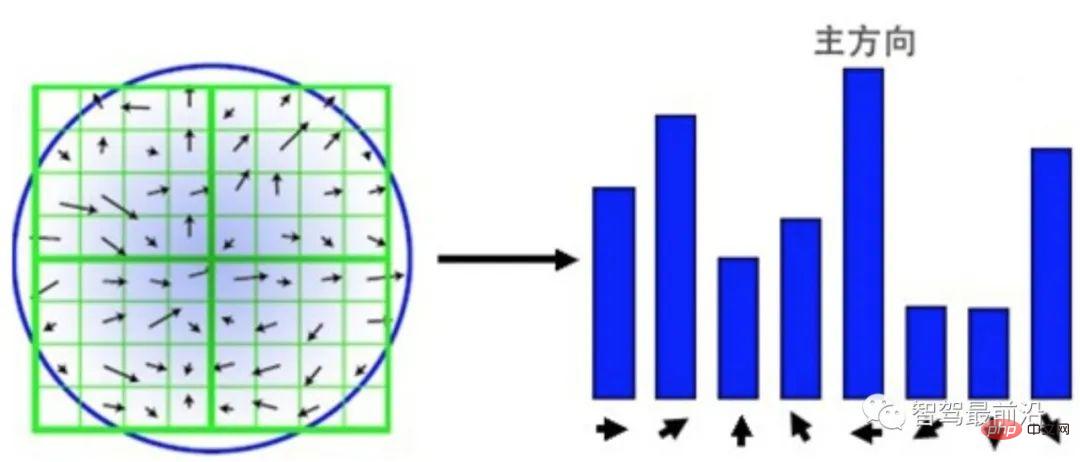
Abbildung 3: SIFT-Deskriptor basierend auf Gradientenblockierungsstatistiken
Binärer Deskriptor
Obwohl nach dem Vorschlag von SIFT einige verbesserte Algorithmen wie SURF, AKAZE usw. entwickelt wurden, ist es selbst heute im Jahr 2019 in einigen Szenarien immer noch schwierig, die Echtzeitanforderungen des Algorithmus zu gewährleisten. Beispielsweise verfügen Handheld-Geräte im Allgemeinen über eine begrenzte Rechenleistung. Beim autonomen Fahren müssen CPU- und GPU-Ressourcen gleichzeitig von mehreren rechenintensiven Modulen geplant werden. Daher ist die Effizienz ein wichtiger Indikator, um die Praktikabilität eines Algorithmus zu prüfen.
Um die Effizienz zu verbessern, haben Wissenschaftler einige binäre Deskriptoren vorgeschlagen. Im Allgemeinen führen diese Methoden Punktproben um Feature-Schlüsselpunkte herum durch. Dann wird die Graustufengröße eines Punktpaares verglichen und das Ergebnis als 0/1 ausgedrückt, wodurch ein N-dimensionaler binärer Beschreibungsvektor gebildet wird, der ein binäres Muster von Merkmalspunkten bildet. Der größte Unterschied zwischen verschiedenen binären Deskriptoren liegt hauptsächlich in den unterschiedlichen Merkmalsabtastmodi und den unterschiedlichen Methoden zur Punktpaarauswahl.
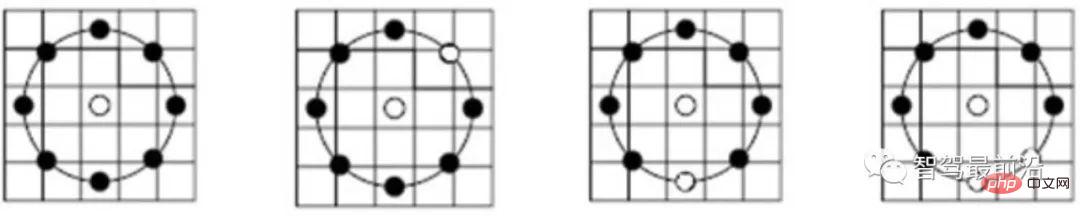
Abbildung 4: LBP-Deskriptor-Unterabtastungsmodus
Wie in Abbildung 4 gezeigt, übernimmt der LBP-Deskriptor eine kreisförmige Abtastung um den Schlüsselpunkt und vergleicht sie mit der Grauskala des zentralen Schlüsselpunkts. Vergleichsoptionen . Die Ergebnisse des Graustufenvergleichs werden auf dem Ring angezeigt, wobei die schwarzen Punkte 0 und die weißen Punkte 1 sind. LBP ist die einfachste Form eines binären Deskriptors, während ORB die BRIEF-Funktion verbessert und derzeit ein häufig verwendeter binärer Deskriptor ist. Wie in Abb. 5 dargestellt, verwendet ORB bei der Auswahl von Punktpaaren eine Zufallsmethode, um lokale Details umfassender zu beschreiben, im Gegensatz zur einfachen Verwendung des Mittelpunkts. Allerdings ist die Korrelation zwischen Punktpaaren relativ groß, wodurch die Unterscheidungskraft des Deskriptors verringert wird. ORB verwendet direkt gierige und erschöpfende Methoden, um dieses Problem zu lösen und zufällige Punktpaare mit geringer Korrelation zu finden. Abbildung 5: Auswahlmodus für ORB-Deskriptor-Punktpaare Bereitstellung einer reguläreren binären Musterkonstruktionsmethode mit integrierten Skaleninformationen. Beispielsweise ahmt der FREAK-Deskriptor das visuelle Abtastmuster des menschlichen Auges nach. Wie in Abb. 6 dargestellt, ist der Wert jedes Abtastpunkts der mittlere Grauwert innerhalb des roten Kreises, und die blaue Linie stellt den Punktpaar-Auswahlplan dar.
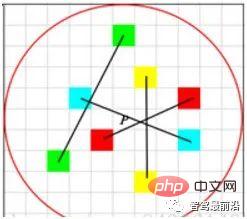
Abbildung 6: FREAK-Deskriptor-Sampling, Punktpaarauswahlmodell
Die hohe Effizienz binärer Deskriptoren spiegelt sich hauptsächlich in drei Aspekten wider.
 (1) Binäre Deskriptoren verwenden binäre Vektoren als Merkmalsbeschreibungen und müssen nur die Größe von Punktpaaren vergleichen, ohne spezifische Gradienten zu berechnen.
(1) Binäre Deskriptoren verwenden binäre Vektoren als Merkmalsbeschreibungen und müssen nur die Größe von Punktpaaren vergleichen, ohne spezifische Gradienten zu berechnen.
(2) Der Vergleich zwischen zwei Deskriptoren kann die Hamming-Distanz (Hamming-Distanz) verwenden, die schneller zu berechnen und einfacher zu optimieren ist.
(3) Da jeder Binärvektor einer Dezimalzahl entspricht, stellt er selbst auch ein Muster dar, ohne dass ein Histogramm zur Darstellung wie bei SIFT verwendet werden muss.
Binäre Deskriptoren sind im Allgemeinen nicht so diskriminierend wie Deskriptoren der SIFT-Familie, aber in bestimmten Szenarien kann die Effizienz in Kombination mit paralleler Programmierung Dutzende oder sogar Hunderte Male höher sein und gleichzeitig ähnliche Unterscheidungsfähigkeiten gewährleisten.
Datenbankerstellung und -abfrage
Die Datenbank kann als Integration von Karte + Index verstanden werden. Karten können aus reinen 2D-Bildern, 3D-Punktwolkenkarten oder einer Kombination aus 2D-Bildern und 3D-Punktwolken bestehen. Bei der Generierung von 3D-Punktwolkenkarten wird hauptsächlich die dreidimensionale Rekonstruktionsmethode SfM (Structure from Motion) verwendet, um 3D-Informationen aus 2D-Zeitreihenbildern abzuleiten. Wenn eine binokulare RGB-D-Kamera Tiefe liefert, können genauere 3D-Punktinformationen erhalten werden. Es enthält auch einige Auswahlstrategien wie Keyframes. Die spezifischen Methoden gehen über den Rahmen dieses Artikels hinaus. Interessierte Schüler können die relevanten Informationen selbst überprüfen. Die Rolle der Datenbank ist:
Fragen Sie für ein Eingabebeobachtungsbild den Kartierungsverlauf (Bild/Punktwolke/Feature-Punkte) über die Datenbank ab, um die Kartenteilmenge (Bild/Punktwolke) zu erhalten, die am wahrscheinlichsten ist (im aktuellen Bild/in den aktuellen Bild-/Feature-Punkten beobachtet), die Karte mit den Beobachtungsinformationen abgleichen, die Transformationsmatrix berechnen und die Pose der Beobachtungskamera ermitteln.
Index ist der Schlüssel zur Beschleunigung dieses Prozesses. Die Datenbanken selbst sind in der Regel riesig. Nehmen Sie als Beispiel den Testbetrieb des Beutelroboters von Meituan im zweiten Stock von Joy City in Chaoyang, Peking. Auch nach der Vorführung wurden fast 80.000 Bilder im Format 900 × 600 verwendet. Angesichts der Echtzeitnatur der Positionierung ist es unmöglich, die Abfrage jedes Mal einzeln mit 80.000 Bildern zu vergleichen. Daher muss die Indexierungstechnologie verwendet werden, um den gesamten Algorithmus zu beschleunigen. Diese Technologie überschneidet sich stark mit Loopback-Tests bei SLAM, Bildabruf und Standorterkennung bei Vision. Im Folgenden werden nur allgemeine Methoden vorgestellt.
Ein Bild enthält mehrere Merkmalspunkte. Die Merkmalspunkte müssen zuerst codiert werden, z. B. mit der VLAD-Codierung (Vector of Local Aggregated Descriptors), und lokale Deskriptoren werden verwendet, um eine globale Beschreibung des Bildes zu erstellen. Verwenden Sie dann Indizes wie kd-tree, um Abfragen auf Bildebene durchzuführen. Natürlich können Codierung und Indizierung auch gleichzeitig durchgeführt werden, z. B. das hierarchische Bag-of-Words-Modell (Bag-of-Words, BoW) + Vorwärtsindex + Rückwärtsindex-Methode.
VLAD-Codierung
VLAD (Vektor lokal aggregierter Deskriptoren) [10] ist, wie in Abb. 7 dargestellt, ein Codebuch (Codebuch), das durch Aggregieren lokaler Deskriptoren und Berechnen der Beschreibung durch Akkumulation gebildet wird zwischen dem Unterwort und dem Codewort (Word) ist eine einfache Methode zur globalen Codierung. Ein 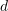 dimensionaler Deskriptor
dimensionaler Deskriptor  wird durch das Codebuch von
wird durch das Codebuch von 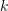 Codewörtern codiert, um einen
Codewörtern codiert, um einen 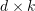 dimensionalen Beschreibungsvektor zu bilden. Der Wert im Vektor ist der Deskriptor und das
dimensionalen Beschreibungsvektor zu bilden. Der Wert im Vektor ist der Deskriptor und das 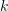 -te Codewort
-te Codewort 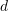 te Dimension. Anschließend wird eine
te Dimension. Anschließend wird eine 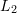 -Normalisierung durchgeführt, um den endgültigen VLAD-Vektor zu bilden.
-Normalisierung durchgeführt, um den endgültigen VLAD-Vektor zu bilden.
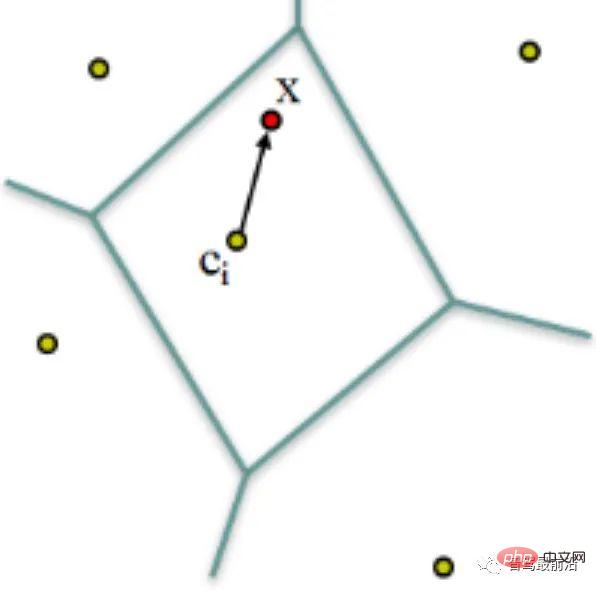
Abbildung 7: VLAD wird durch den Abstand zwischen dem Deskriptor und dem Codewort codiert
DenseVLAD[11] und NetVLAD[12] werden hier speziell vorgestellt. Torii et al. haben bewiesen, dass DenseSIFT Standard-SIFT bei beiden Abfrageabgleichen übertrifft. DenseVLAD extrahiert SIFT-Punkte auf vier Skalen in einem gitterartigen Abtastmuster mit 2-Pixel-Intervallen. Stichproben Sie weltweit zufällig 25 Millionen Deskriptoren ab und verwenden Sie den K-Means-Algorithmus, um ein Codebuch mit 128 Codewörtern zu generieren. Der VLAD-Vektor wird nach der Normalisierung mithilfe der PCA (Hauptkomponentenanalyse) dimensional reduziert, um den endgültigen 4096-dimensionalen DenseVLAD-Vektor zu bilden. Wie in Abb. 8 dargestellt, ist die Anzahl der inneren Punkte (grün) nach dem Abgleich mit DenseSIFT größer.

Abbildung 8: DenseSIFT- und Standard-SIFT-Feature-Punkte, Vergleich der inneren Punkte (grün) nach dem Matching
NetVLAD fügt VLAD Überwachungsinformationen hinzu, um die Unterscheidbarkeit der VLAD-Codierung zu verbessern. Nehmen Sie, wie in Abb. 9 dargestellt, an, dass die beiden Deskriptoren Rot und Grün von zwei Bildern stammen, die nicht zusammenpassen sollten. Da beide einen größeren Radius und einen ähnlichen Abstand vom VLAD-Zentrum (×) haben, sind ihre codierten Werte nach der L2-Normalisierung sehr ähnlich. Nach dem Hinzufügen der Überwachungsinformationen, dass die Bilder, die den roten und grünen Deskriptoren entsprechen, nicht übereinstimmen, kann der von NetVLAD generierte Mittelpunkt (★) die beiden Deskriptoren besser unterscheiden und ihre codierte Abstandsdifferenz (Radius) erhöhen.
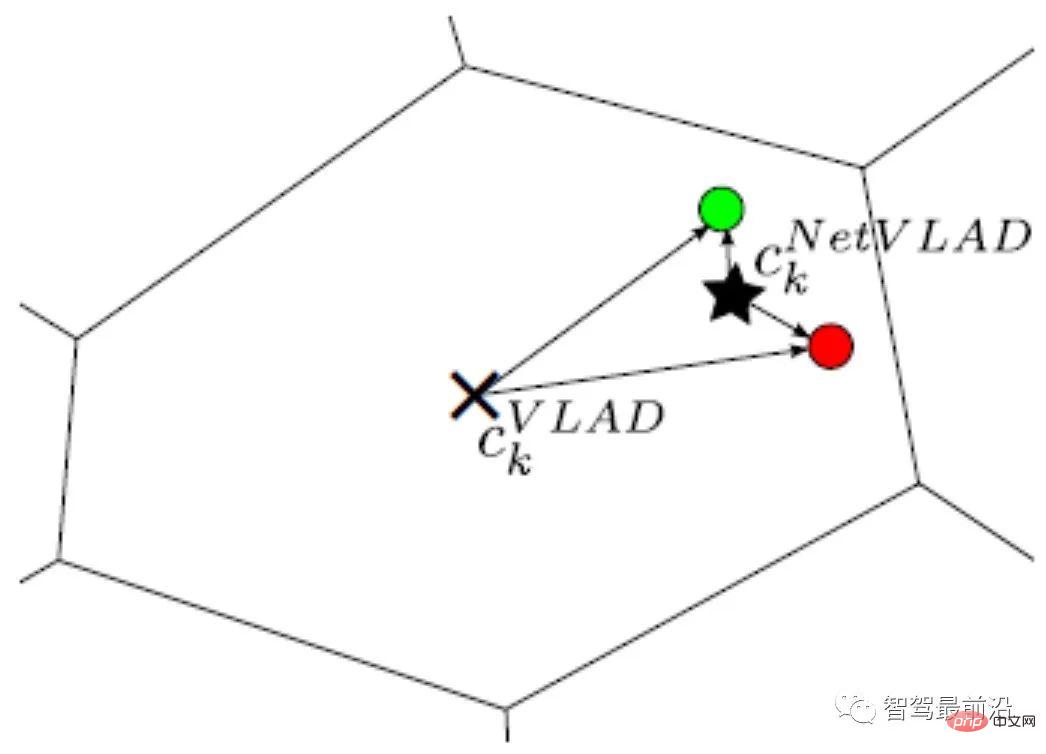
Abbildung 9: Vergleich des NetVLAD-Clusterzentrums (×) und des VLAD-Clusterzentrums (★) BoW-Kodierung + Index Basierend auf den Eigenschaften des Bag-of-Words-Modells BoW [ 13, 14] Codierung und ihre Designideen spielen eine entscheidende Rolle bei der Entwicklung von Computer Vision und werden hier nicht vorgestellt. In diesem Artikel wird als Beispiel ein 2D-Abfragebildabgleich mit einer 2D-Bilddatenbank verwendet, um ein gemeinsames integriertes BoW-Kodierungs- und Indizierungsmodell vorzustellen. Wie in Abb. 10 gezeigt, wird das Wörterbuch (Vokabular) mithilfe einer hierarchischen Methode generiert. Für alle Deskriptoren im Datensatz wird der Raum gemäß einer Baumstruktur unterteilt und jede Ebene wird durch k-Mittel-Clustering berechnet. Die letzten Blattknoten entsprechen Codewörtern (in Abb. 10 gibt es 9 Codewörter).
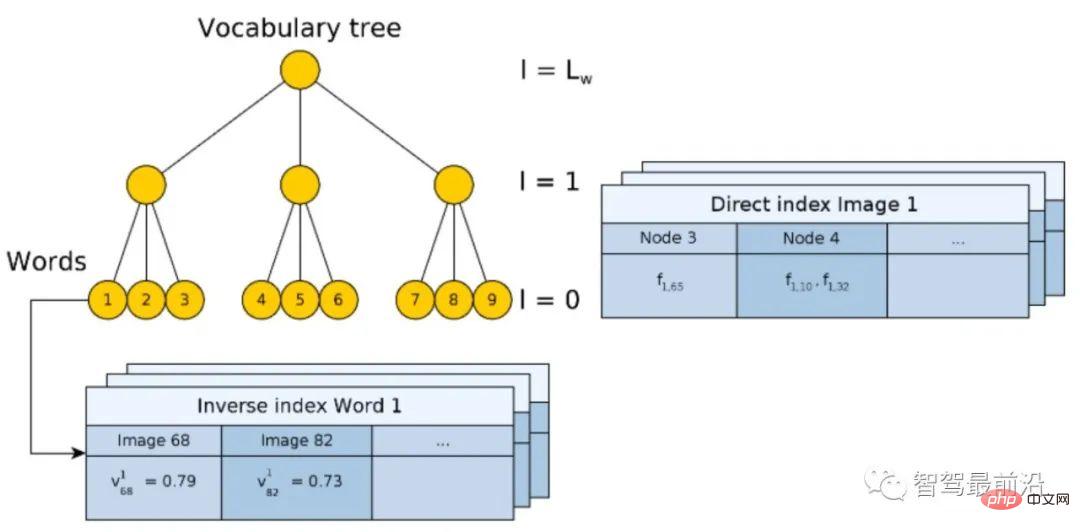
Abbildung 10: Hierarchisches BoW-Modell mit Vorwärtsindex und Rückwärtsindex
Der Konstruktionsprozess des Baums ist eigentlich der Prozess der Kodierung des Originalbilds. Die Kodierung selbst beschleunigt den Suchvorgang jedoch nicht. Ähnlich wie bei VLAD muss sie dennoch einzeln mit den Bildern in der Datenbank verglichen werden. Daher wird hier ein inverser Index (Inversindex) entworfen, der keinen Vergleich der codierten Vektoren erfordert. Das Prinzip ist in Abb. 11 dargestellt. Für ein Abfragebild (Query Image) wird der extrahierte Deskriptor in BoW eingegeben und fällt schließlich in den Codewort-Blattknoten (Visual Word) k. Jedes Codewort entspricht einem Index, der das Gewicht des Codeworts 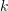 bis zum
bis zum  ten Bild in der Datenbank
ten Bild in der Datenbank 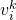 aufzeichnet (Abb. 10). Hier wird das Gewicht mithilfe von TF-IDF (Termhäufigkeit – inverse Dokumenthäufigkeit) berechnet. Das heißt, wenn ein Wort
aufzeichnet (Abb. 10). Hier wird das Gewicht mithilfe von TF-IDF (Termhäufigkeit – inverse Dokumenthäufigkeit) berechnet. Das heißt, wenn ein Wort 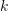 häufig in einem bestimmten Bild
häufig in einem bestimmten Bild  vorkommt und in anderen Bildern selten vorkommt, dann hat dieses Wort eine bessere Bildunterscheidbarkeit und einen höheren Gewichtungswert
vorkommt und in anderen Bildern selten vorkommt, dann hat dieses Wort eine bessere Bildunterscheidbarkeit und einen höheren Gewichtungswert 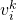 . Abschließend wird das passende Bild über den Abstimmungsmechanismus ausgewählt. Es ist auch wichtig zu beachten, dass der umgekehrte Index nicht unbedingt auf dem baumstrukturierten BoW aufbaut, sondern lediglich eine Methode zur schnellen Abfrage bereitstellt.
. Abschließend wird das passende Bild über den Abstimmungsmechanismus ausgewählt. Es ist auch wichtig zu beachten, dass der umgekehrte Index nicht unbedingt auf dem baumstrukturierten BoW aufbaut, sondern lediglich eine Methode zur schnellen Abfrage bereitstellt.
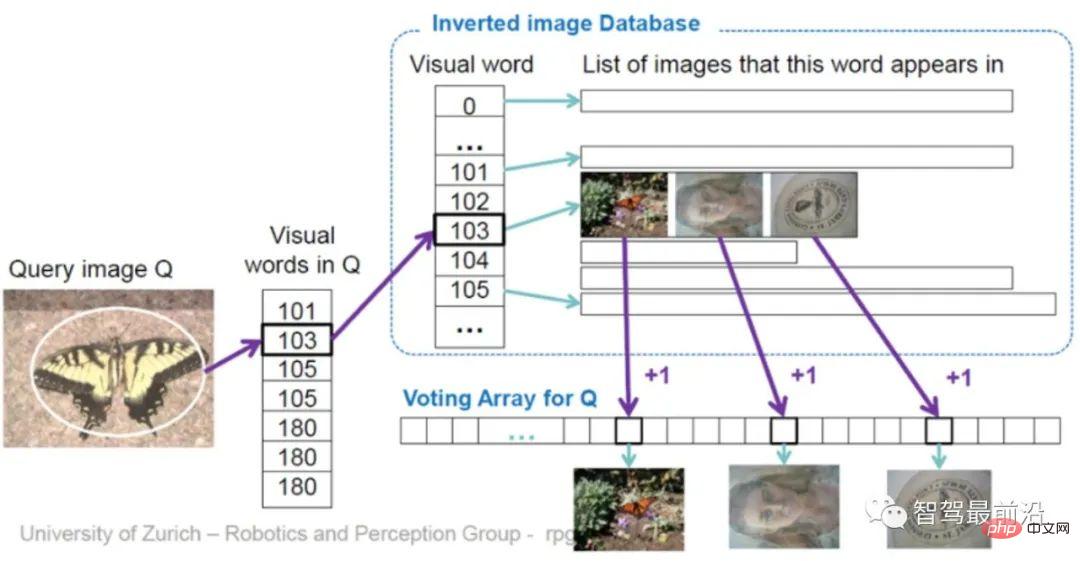
Abbildung 11: Bilder direkt über Reverse Index + Abstimmungsmechanismus abfragen
Die Hauptfunktion des Direktindex besteht darin, beim Erstellen des BoW aufzuzeichnen, in welche Knoten die Merkmalspunkte des Datenbankbilds fallen. Auf diese Weise müssen Sie die Merkmalspunkte nicht berechnen, wenn das Bild abgefragt wird Sie können den Index direkt verwenden, um Merkmalspunkte zu extrahieren.
3D-Punktwolkenabfrage
Bei der 2D-Bildabfrage wird das Bild zunächst auf semantischer Ebene abgefragt, sodass der räumliche Bereich der Merkmalspunkte durch das Bild eingeschränkt werden kann. Die Abfrage von 3D-Punktwolken unterliegt keinen solchen Einschränkungen und weist daher viele Schwierigkeiten auf. Wenn Sie räumliche Kontinuität berücksichtigen müssen, ob alle abgefragten Punkte innerhalb des beobachtbaren Bereichs liegen usw. Hier stellen wir nur die von Sattler auf der TPAMI 2016 veröffentlichte Methode [15] vor. Nach Jahren des Polierens ist dieses Methodengerüst relativ einfach und vollständig. Da sich die Suchschritte der Wörterbuchkodierung mit dem Inhalt im vorherigen Abschnitt überschneiden, werden hier nur die beiden Mechanismen der aktiven Suche und der Sichtbarkeitsfilterung vorgestellt.
Die aktive Suche dient hauptsächlich dazu, die übereinstimmenden 3D-Punkte so nah wie möglich im Raum zu platzieren und eine geometrische Bedeutung zu haben. Wie in Abb. 12 dargestellt, wird der rote Punkt durch eine Reihe von Kodierungs- und Verfeinerungsprozessen einem Punkt in der Punktwolke zugeordnet (rote Linie). Gemäß dem vorgeschlagenen Priorisierungsrahmen wird ein 3D-Punkt mit der höchsten Wahrscheinlichkeit aus der Punktwolke gefunden und umgekehrt (blaue Linie) mit einem entsprechenden 2D-Punkt im Abfragebild übereinstimmt. Abbildung 12: Aktive Suche Damit die abgeglichenen Punkte für die Kamera so gut wie möglich sichtbar sind (die Positionierung erfolgt unbeaufsichtigt und es ist nicht möglich zu wissen, ob der abgeglichene Punkt korrekt ist). Die hier angewandte Methode besteht darin, ein zweiteiliges Sichtbarkeitsdiagramm zu erstellen, wenn SfM zum Erstellen einer 3D-Punktwolkenkarte verwendet wird. Wie in Abb. 13 (links) dargestellt, entsteht eine topologische Beziehung, wenn ein Punkt gleichzeitig von zwei Kameras beobachtet werden kann. In Abb. 13 (Mitte) handelt es sich bei den blauen Punkten um übereinstimmende Punkte, die aus Beobachtungsperspektive widersprüchlich sind. Durch die Durchführung von Graph-Clustering auf der vorhandenen Topologie werden Kameras in zwei Gruppen gruppiert, wie in Abb. 13 (rechts) dargestellt. Auf diese Weise können neue graphtopologische Beziehungen generiert werden. Anschließend filtern wir die Punkte heraus, die mit hoher Wahrscheinlichkeit unsichtbar sind, indem wir die Überlappung zwischen den einzelnen Unterdiagrammen beurteilen.
 Es ist zu beachten, dass Fernglaskameras und RGB-D-Kameras zwar Tiefe ermitteln können und durch Abfragen von 2D-Bildern innerhalb eines begrenzten Bereichs auch 3D-Merkmalspunktkoordinaten ermittelt werden können, Innenmaterialien jedoch aufgrund aktueller technischer Einschränkungen komplex und im Freien groß sind Bei maßstabsgetreuen Szenen ist die Tiefe nicht zuverlässig. Daher ist der Abgleich von 2D-Bildpunkten und 3D-Punktwolkenkarten immer noch eine wichtige Methode.
Es ist zu beachten, dass Fernglaskameras und RGB-D-Kameras zwar Tiefe ermitteln können und durch Abfragen von 2D-Bildern innerhalb eines begrenzten Bereichs auch 3D-Merkmalspunktkoordinaten ermittelt werden können, Innenmaterialien jedoch aufgrund aktueller technischer Einschränkungen komplex und im Freien groß sind Bei maßstabsgetreuen Szenen ist die Tiefe nicht zuverlässig. Daher ist der Abgleich von 2D-Bildpunkten und 3D-Punktwolkenkarten immer noch eine wichtige Methode.
Feature-Point-Matching
Der Feature-Point-Matching-Prozess kann in Datenbankabfragen adaptiv abgeschlossen werden, was bei Abfragen, die auf 3D-Strukturen basieren, häufiger der Fall ist. Das Matching kann auch separat nach der Abfrage durchgeführt werden, was bei 2D-bildbasierten Abfragen häufiger vorkommt. Der Zweck des Merkmalsabgleichs besteht darin, passende Punktpaare für nachfolgende Transformationsmatrixberechnungen bereitzustellen, um eine Posenberechnung zu erreichen. 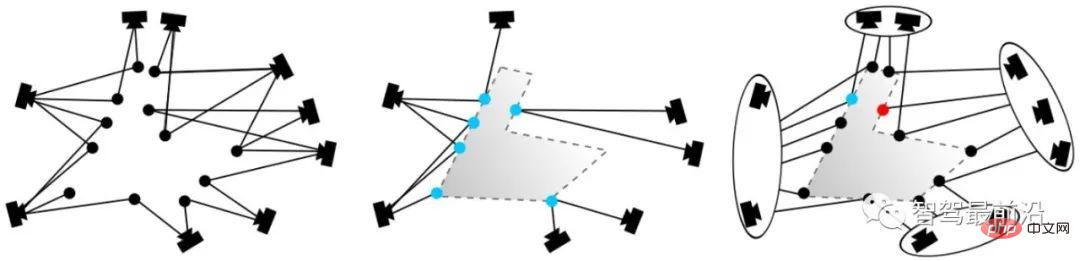
Klassischer RANSAC
Random Sample Consensus Algorithm (RANSAC) [16] ist ein klassischer Datenfilter- und Parameteranpassungsalgorithmus. Es geht davon aus, dass die Verteilung der Daten (Inliers) einem bestimmten mathematischen Modell entspricht, und entfernt durch iterative Berechnungen Ausreißer und Rauschpunkte und erhält gleichzeitig die besten Modellparameter hinsichtlich der Wahrscheinlichkeit. Bei der globalen Positionierung beziehen sich innere Punkte auf korrekte Übereinstimmungen, äußere Punkte auf falsche Übereinstimmungen und das parametrische Modell bezieht sich auf die räumliche Transformationsmatrix übereinstimmender Punktpaare. Wie in Abb. 14 gezeigt, ist die Übereinstimmung nach der Optimierung durch den RANSAC-Algorithmus sinnvoller. Die passende Teilmenge, die RANSAC zu finden erwartet, muss zwei Indikatoren erfüllen: Der Fehler bei der Neuprojektion des inneren Punkts ist so klein wie möglich; die Anzahl der inneren Punkte ist so groß wie möglich. Der grundlegende Prozess ist also wie folgt:① Probenahme der ersten Teilmenge.
② Berechnen Sie die Transformationsmatrix.
③ Berechnen Sie den Reprojektionsfehler des Übereinstimmungspunkts gemäß der Transformationsmatrix.
④ Punkte mit großen Fehlern entfernen
⑤ Schleife ①-④, um die passende Lösung beizubehalten, die dem Index am besten entspricht.

Abbildung 14: (Oben) Original-Feature-Matching; (Unten) Matching optimiert durch RANSAC-Algorithmus#🎜 🎜#
Unter diesen wird die anfängliche Kandidatenübereinstimmung basierend auf dem Abstand zwischen Deskriptoren generiert, aber der Neuprojektionsfehler hängt nur mit der räumlichen Position der Schlüsselpunkte zusammen und hat nichts damit zu tun Deskriptoren selbst. Informationen zur spezifischen Projektionsmatrixmethode finden Sie unter „2.4 Posenberechnung“. Es sollte darauf hingewiesen werden, dass der RANSAC-Algorithmus vom ursprünglichen Übereinstimmungsfehler und der Parameterauswahl beeinflusst wird. Er kann nur sicherstellen, dass die Wahrscheinlichkeit des Algorithmus hoch genug ist, um angemessen zu sein, und erzielt möglicherweise nicht unbedingt das optimale Ergebnis. Zu den Algorithmusparametern gehören hauptsächlich der Schwellenwert und die Anzahl der Iterationen. Die Wahrscheinlichkeit, dass RANSAC ein glaubwürdiges Modell erhält, ist direkt proportional zur Anzahl der Iterationen, und die Anzahl der erhaltenen Übereinstimmungen ist umgekehrt proportional zum Schwellenwert. Daher kann es im tatsächlichen Einsatz erforderlich sein, wiederholt verschiedene Parametereinstellungen auszuprobieren, um bessere Ergebnisse zu erzielen.
Wissenschaftler haben viele Verbesserungen am klassischen RANSAC-Algorithmus vorgenommen. Wie in Abb. 15 gezeigt, wird das Strukturdiagramm des globalen RANSAC (Universal-RANSAC) [17] vorgeschlagen Es wurde eine universelle RANSAC-Architektur geschaffen, die nahezu alle Aspekte von RANSAC-Verbesserungen abdeckt, wie z. B. Vorfilterung, minimale Teilmengen-Stichprobe, zuverlässige Modellgenerierung aus minimalen Teilmengen, Parameterüberprüfung und Modellverfeinerung.
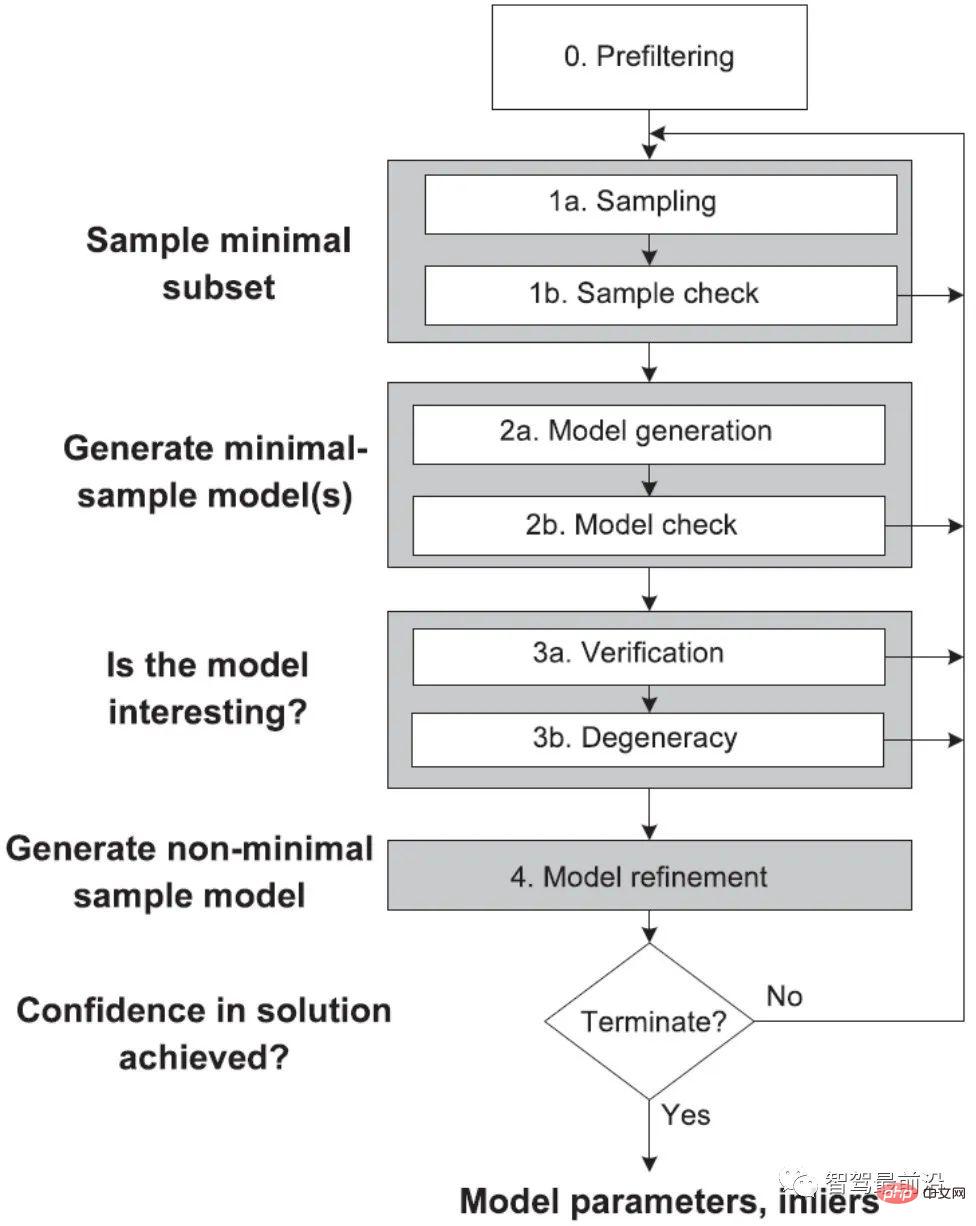
Abbildung 15: Allgemeines Universal-RANSAC-Algorithmus-Framework# 🎜🎜#
differenzierbares RANSAC
Da manuelle Deskriptoren bei der Positionierungsfeldleistung immer noch eine gute Leistung erbringen, also Einige Wissenschaftler begannen damit, bestimmte Teile des Algorithmus-Frameworks mithilfe von Deep Learning zu ersetzen, anstatt direkt End-to-End-Modelle zur Posenschätzung zu verwenden, um traditionelle Methoden vollständig zu ersetzen. Differentiable RANSAC (Differentiable RANSAC, DSAC) [18] zielt darauf ab, die deterministische Hypothesenauswahl durch eine probabilistische Hypothesenauswahl zu ersetzen, sodass der RANSAC-Prozess abgeleitet werden kann. Der Prozess ist in Abb. 16 dargestellt, in dem der Schritt „Scoring“ weiterhin eine Neuprojektion verwendet Fehler Als Indikator besteht der Unterschied darin, dass der Fehler auf dem gesamten Bild und nicht auf Merkmalspunkten basiert und der ursprüngliche Prozess der Überprüfung der Merkmalspunktübereinstimmung durch einen Prozess der direkten Überprüfung der Kamerapositionshypothese h mit Wahrscheinlichkeit ersetzt wird. Obwohl die aktuelle Methode relativ große Einschränkungen aufweist, bietet DSAC eine praktikable Idee, wie Vorkenntnisse zum aktuellen Rahmen für unbeaufsichtigte Positionierungsalgorithmen hinzugefügt werden können. #🎜🎜 ##### 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜#ABBILDUNG 16: Differential-Ransac-Algorithmus-Framework#🎜🎜 ## 🎜🎜. ##🎜🎜 #Positionsberechnung
Für das korrekte passende Punktpaar, das erhalten wurde, muss die entsprechende Transformationsmatrix durch geometrische Einschränkungen berechnet werden (Transformation Matrix). Da die Punktkoordinaten in der Datenbank und die Kameraposition zum Zeitpunkt der Abtastung bekannt sind, kann die aktuelle Kameraposition durch Anpassen der Transformationsmatrix des Punktes an den Kartenpunkt ermittelt werden. Einige grundlegende Symbole werden hier definiert. Die internen Parameter der Kamera sind 
, und die homogene Form des Transformationsmoments ist:
#🎜 🎜#
Darunter ist die Rotationsmatrix und  # 🎜🎜# ist die Übersetzungsmatrix.
# 🎜🎜# ist die Übersetzungsmatrix.  2.4.1 2D-2D-Transformationsmatrixberechnung
2.4.1 2D-2D-Transformationsmatrixberechnung
), ihre Koordinaten auf der normalisierten Ebene sind (
) und die entsprechende Transformationsmatrix muss durch epipolare Einschränkungen berechnet werden. Wie in Abb. 17 gezeigt, besteht seine geometrische Bedeutung darin, dass 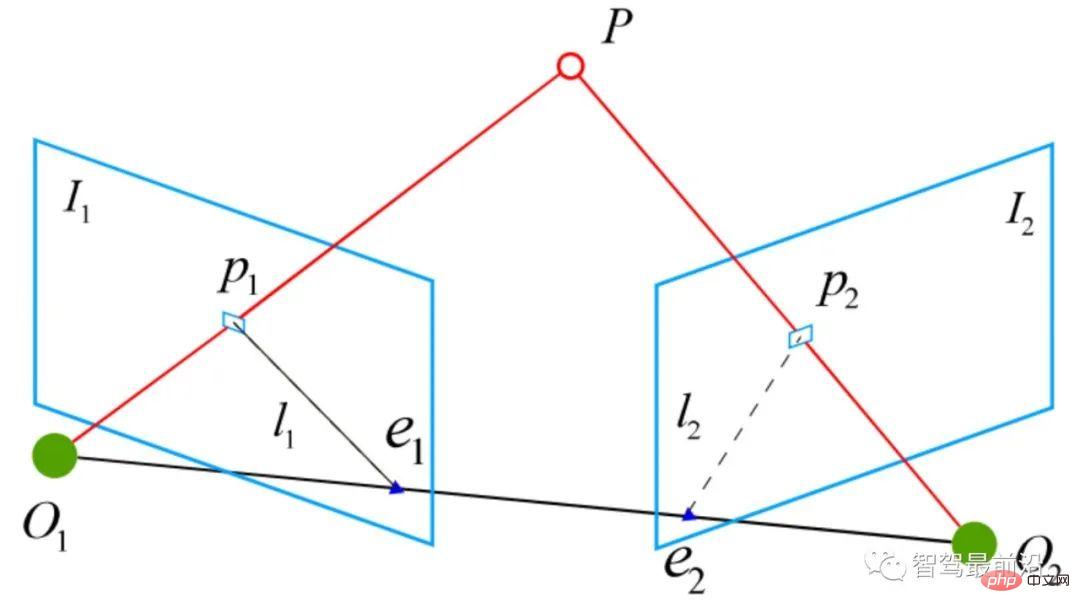
drei koplanare Flächen sind, die auch Polarebene genannt werden, Grundlinie und
Polarlinie. Die epipolare Einschränkung umfasst sowohl Translation als auch Rotation, die wie folgt definiert ist: 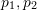
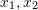 wobei
wobei 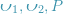 die Koordinate von
die Koordinate von 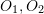 auf der normalisierten Ebene ist und ∧ der äußere Produktoperator ist. Zählen Sie den mittleren Teil der Formel als Grundmatrix
auf der normalisierten Ebene ist und ∧ der äußere Produktoperator ist. Zählen Sie den mittleren Teil der Formel als Grundmatrix 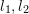 und als essentielle Matrix
und als essentielle Matrix
, dann haben wir: 
Da die essentielle Matrix 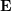 keine Skaleninformationen hat, gilt die epipolare Einschränkung weiterhin, nachdem E mit einer beliebigen Konstante ungleich Null multipliziert wird.
keine Skaleninformationen hat, gilt die epipolare Einschränkung weiterhin, nachdem E mit einer beliebigen Konstante ungleich Null multipliziert wird. 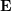 kann mit dem klassischen 8-Punkte-Algorithmus (Acht-Punkte-Algorithmus) gelöst und dann zerlegt werden, um
kann mit dem klassischen 8-Punkte-Algorithmus (Acht-Punkte-Algorithmus) gelöst und dann zerlegt werden, um 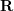 , #🎜 zu erhalten 🎜##🎜 🎜#. Daher ist ersichtlich, dass die 2D-2D-Transformationsmatrix-Lösungsmethode zwei Mängel aufweist. Erstens weist das monokulare Sehen Skalenunsicherheit auf, und die Skaleninformationen müssen während der Initialisierung durch
, #🎜 zu erhalten 🎜##🎜 🎜#. Daher ist ersichtlich, dass die 2D-2D-Transformationsmatrix-Lösungsmethode zwei Mängel aufweist. Erstens weist das monokulare Sehen Skalenunsicherheit auf, und die Skaleninformationen müssen während der Initialisierung durch 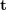 bereitgestellt werden . Dementsprechend kann die monokulare Initialisierung nicht nur eine reine Rotation sein, sondern muss auch einen ausreichenden Übersetzungsgrad aufweisen, da sonst
bereitgestellt werden . Dementsprechend kann die monokulare Initialisierung nicht nur eine reine Rotation sein, sondern muss auch einen ausreichenden Übersetzungsgrad aufweisen, da sonst 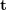 Null wird.
Null wird. 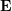
2.4.2 2D-3D-Transformationsmatrixberechnung
2D -3D-Matching ist eine wichtige Methode zur Posenschätzung. Im Allgemeinen wird die PnP-Methode verwendet, das heißt, es ist bekannt, dass die Transformationsmatrix für die 2D-3D-Übereinstimmungspunkte löst, um die Kameraposition zu erhalten. Wir projizieren den 3D-Punkt P(X, Y, Z) auf die Bildebene der Kamera ( ):
): 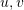
 # 🎜🎜# Unter ihnen ist
# 🎜🎜# Unter ihnen ist
die Skala,  . Die Lösung dieser Gleichung kann auf ein lineares Gleichungsproblem reduziert werden, und jedes Merkmal kann zwei lineare Einschränkungen bereitstellen: #Auf diese Weise können mindestens 6 Paare von Übereinstimmungspunkten gelöst werden, und wenn die Anzahl der Übereinstimmungspunkte größer als 6 ist , Methoden wie SVD können verwendet werden, um das Problem durch die Konstruktion kleinster Quadrate zu lösen. Die P3P-Methode kann als Sonderlösung der PnP-Methode betrachtet werden. Wie in Abb. 18 dargestellt, nutzt sie die Ähnlichkeitseigenschaften von Dreiecken, um weitere Einschränkungen hinzuzufügen, und benötigt zur Lösung des Problems nur drei Punktpaare. Andere Lösungsmethoden umfassen die direkte lineare Transformation (DLT), die EPnP-Methode (Efficient PnP) und die UPnP-Methode (Unkalibriertes PnP) usw. Im Vergleich zu den oben genannten linearen Optimierungsmethoden werden auch nichtlineare Optimierungsmethoden wie Bundle Adjustment (BA) häufig verwendet. Die BA-Methode ist eine Art „Einheitslösung“ im visuellen SLAM. Sie kann mehrere Variablen gleichzeitig optimieren, wodurch die durch lokale Fehler verursachte Systeminstabilität bis zu einem gewissen Grad gemindert werden kann Relevante Informationen für ein tieferes Verständnis.
. Die Lösung dieser Gleichung kann auf ein lineares Gleichungsproblem reduziert werden, und jedes Merkmal kann zwei lineare Einschränkungen bereitstellen: #Auf diese Weise können mindestens 6 Paare von Übereinstimmungspunkten gelöst werden, und wenn die Anzahl der Übereinstimmungspunkte größer als 6 ist , Methoden wie SVD können verwendet werden, um das Problem durch die Konstruktion kleinster Quadrate zu lösen. Die P3P-Methode kann als Sonderlösung der PnP-Methode betrachtet werden. Wie in Abb. 18 dargestellt, nutzt sie die Ähnlichkeitseigenschaften von Dreiecken, um weitere Einschränkungen hinzuzufügen, und benötigt zur Lösung des Problems nur drei Punktpaare. Andere Lösungsmethoden umfassen die direkte lineare Transformation (DLT), die EPnP-Methode (Efficient PnP) und die UPnP-Methode (Unkalibriertes PnP) usw. Im Vergleich zu den oben genannten linearen Optimierungsmethoden werden auch nichtlineare Optimierungsmethoden wie Bundle Adjustment (BA) häufig verwendet. Die BA-Methode ist eine Art „Einheitslösung“ im visuellen SLAM. Sie kann mehrere Variablen gleichzeitig optimieren, wodurch die durch lokale Fehler verursachte Systeminstabilität bis zu einem gewissen Grad gemindert werden kann Relevante Informationen für ein tieferes Verständnis. 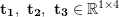

# 🎜 🎜#
3D-3D-Transformationsmatrixberechnung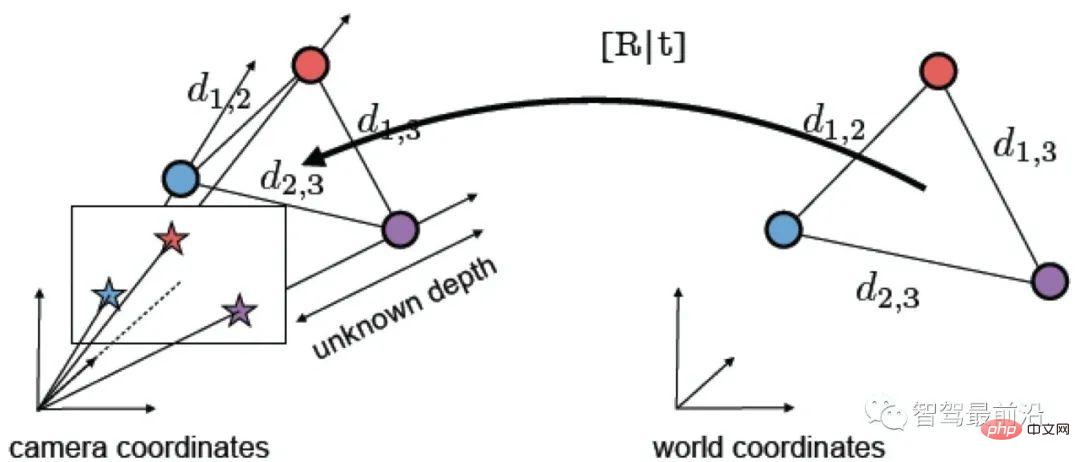
Die Transformationsmatrix zwischen 3D-Punkten kann mithilfe des ICP-Algorithmus (Iterative Closest Point) gelöst werden. Unter der Annahme, dass das Ergebnis der Punktpaaranpassung (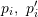 ) korrekt ist, sollte die erhaltene Transformationsmatrix den Neuprojektionsfehler minimieren
) korrekt ist, sollte die erhaltene Transformationsmatrix den Neuprojektionsfehler minimieren 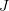 . Sie können SVD verwenden, um das Problem der kleinsten Quadrate zu lösen:
. Sie können SVD verwenden, um das Problem der kleinsten Quadrate zu lösen:
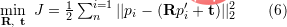
oder die nichtlineare Optimierungsmethode Bundle Adjustment basierend auf der Lie-Algebra verwenden, um
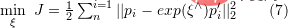
zu lösen, wobei  die Kameraposition darstellt. Das Optimierungsziel ähnelt hier dem der Bündelanpassung beim 2D-3D-Matching, es besteht jedoch keine Notwendigkeit, die kamerainternen Parameter zu berücksichtigen
die Kameraposition darstellt. Das Optimierungsziel ähnelt hier dem der Bündelanpassung beim 2D-3D-Matching, es besteht jedoch keine Notwendigkeit, die kamerainternen Parameter zu berücksichtigen  , da die 2D-Punkte auf dem Originalbild von der Kamerabildebene durch das Fernglas verschoben wurden Kamera oder RGB-D-Tiefenkamera. Projiziert in eine 3D-Welt.
, da die 2D-Punkte auf dem Originalbild von der Kamerabildebene durch das Fernglas verschoben wurden Kamera oder RGB-D-Tiefenkamera. Projiziert in eine 3D-Welt.
Das ICP-Problem hat nachweislich eine einzigartige Lösung und unendlich viele Lösungen. Wenn es eine eindeutige Lösung gibt, entspricht die Optimierungsfunktion daher einer konvexen Funktion, und der Mindestwert ist die globale optimale Lösung. Unabhängig davon, welche Art von Initialisierung verwendet wird, kann diese eindeutige Lösung erhalten werden. Dies ist einer der großen Vorteile der ICP-Methode.
In diesem Artikel wird der Posenschätzungsalgorithmus basierend auf Merkmalspunkten aus vier Aspekten vorgestellt: Bildbeschreibung, Zuordnungsabfrage, Merkmalsabgleich und Posenberechnung. Obwohl die traditionelle visuelle globale Positionierungsmethode in praktischen Anwendungen immer noch die erste Wahl ist, basiert die traditionelle Methode auf der Prämisse, dass die Merkmalspunkte korrekt definiert, korrekt extrahiert, korrekt abgeglichen und korrekt beobachtet werden. Diese Prämisse ist für die Vision sehr wichtig selbst. Es ist eine große Herausforderung. Zweitens erfordert die traditionelle Methode ein mehrstufiges Framework und keine End-to-End-Methode. Daher sind für jede Verbindung und die Interaktion zwischen Verbindungen zahlreiche Parameteranpassungen erforderlich, und die Technologie jeder Verbindung kann als separate Forschungsrichtung verwendet werden. In der tatsächlichen Anwendung müssen viele Tricks für bestimmte Szenarien hinzugefügt werden, was das Engineering komplexer macht.
Und die Erwartungen der Menschen an die End-to-End-Methode haben zu Netzwerken wie PoseNet, VLocNet, HourglassNet usw. geführt, die bei Benchmarks gute Ergebnisse erzielt haben. Der Autor ist der Ansicht, dass es bei der aktuellen End-to-End-Methode immer noch viele Probleme gibt. Die Hauptprobleme sind, dass der Verlustfunktion geometrische Einschränkungen fehlen und der Posenraum mit 6 Freiheitsgraden beim Erstellen der Karte nicht kontinuierlich ist. und es ist schwierig, eine gute Zuordnung mit dem Eingaberaum zu erstellen, und es mangelt an entsprechender Positionshaltungsregression, Verfeinerungsmechanismus usw. Es lässt sich nicht leugnen, dass Deep Learning als leistungsfähigstes Modellierungswerkzeug für den nichtlinearen Raum in Zukunft verstärkt im Bereich der Positionierung auftauchen wird.
Zurück zur visuellen Positionierung selbst, denn die wichtigsten Vorteile des Sehens sind niedrige Kosten, reichhaltige Semantik und wenige Einschränkungen bei den Nutzungsszenarien. Daher werden Positionierungsfusionslösungen, die sich auf das Sehen konzentrieren und durch andere kostengünstige Sensoren ergänzt werden, auch in Zukunft ein wichtiges Thema sein.
Das obige ist der detaillierte Inhalt vonGlobale Positionierungstechnologie basierend auf Merkmalspunkten beim autonomen Fahren mithilfe der Wanzi-Analyse. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1666
1666
 14
14
 1425
1425
 52
52
 1327
1327
 25
25
 1273
1273
 29
29
 1252
1252
 24
24
 Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Warum ist Gaussian Splatting beim autonomen Fahren so beliebt, dass NeRF allmählich aufgegeben wird?
Jan 17, 2024 pm 02:57 PM
Oben geschrieben und persönliches Verständnis des Autors. Dreidimensionales Gaussplatting (3DGS) ist eine transformative Technologie, die in den letzten Jahren in den Bereichen explizite Strahlungsfelder und Computergrafik entstanden ist. Diese innovative Methode zeichnet sich durch die Verwendung von Millionen von 3D-Gaußkurven aus, was sich stark von der Neural Radiation Field (NeRF)-Methode unterscheidet, die hauptsächlich ein implizites koordinatenbasiertes Modell verwendet, um räumliche Koordinaten auf Pixelwerte abzubilden. Mit seiner expliziten Szenendarstellung und differenzierbaren Rendering-Algorithmen garantiert 3DGS nicht nur Echtzeit-Rendering-Fähigkeiten, sondern führt auch ein beispielloses Maß an Kontrolle und Szenenbearbeitung ein. Dies positioniert 3DGS als potenziellen Game-Changer für die 3D-Rekonstruktion und -Darstellung der nächsten Generation. Zu diesem Zweck geben wir erstmals einen systematischen Überblick über die neuesten Entwicklungen und Anliegen im Bereich 3DGS.
 Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
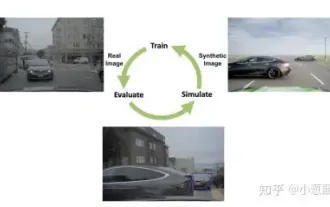
Wie lässt sich das Long-Tail-Problem in autonomen Fahrszenarien lösen?
Jun 02, 2024 pm 02:44 PM
Gestern wurde ich während des Interviews gefragt, ob ich irgendwelche Long-Tail-Fragen gestellt hätte, also dachte ich, ich würde eine kurze Zusammenfassung geben. Das Long-Tail-Problem des autonomen Fahrens bezieht sich auf Randfälle bei autonomen Fahrzeugen, also mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. Das wahrgenommene Long-Tail-Problem ist einer der Hauptgründe, die derzeit den betrieblichen Designbereich intelligenter autonomer Einzelfahrzeugfahrzeuge einschränken. Die zugrunde liegende Architektur und die meisten technischen Probleme des autonomen Fahrens wurden gelöst, und die verbleibenden 5 % der Long-Tail-Probleme wurden nach und nach zum Schlüssel zur Einschränkung der Entwicklung des autonomen Fahrens. Zu diesen Problemen gehören eine Vielzahl fragmentierter Szenarien, Extremsituationen und unvorhersehbares menschliches Verhalten. Der „Long Tail“ von Randszenarien beim autonomen Fahren bezieht sich auf Randfälle in autonomen Fahrzeugen (AVs). Randfälle sind mögliche Szenarien mit geringer Eintrittswahrscheinlichkeit. diese seltenen Ereignisse
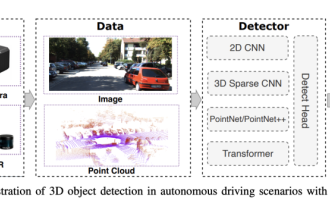 Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
Kamera oder Lidar wählen? Eine aktuelle Übersicht über die Erzielung einer robusten 3D-Objekterkennung
Jan 26, 2024 am 11:18 AM
0. Vorab geschrieben&& Persönliches Verständnis, dass autonome Fahrsysteme auf fortschrittlichen Wahrnehmungs-, Entscheidungs- und Steuerungstechnologien beruhen, indem sie verschiedene Sensoren (wie Kameras, Lidar, Radar usw.) verwenden, um die Umgebung wahrzunehmen, und Algorithmen und Modelle verwenden für Echtzeitanalysen und Entscheidungsfindung. Dies ermöglicht es Fahrzeugen, Verkehrszeichen zu erkennen, andere Fahrzeuge zu erkennen und zu verfolgen, das Verhalten von Fußgängern vorherzusagen usw. und sich so sicher an komplexe Verkehrsumgebungen anzupassen. Diese Technologie erregt derzeit große Aufmerksamkeit und gilt als wichtiger Entwicklungsbereich für die Zukunft des Transportwesens . eins. Aber was autonomes Fahren schwierig macht, ist herauszufinden, wie man dem Auto klarmachen kann, was um es herum passiert. Dies erfordert, dass der dreidimensionale Objekterkennungsalgorithmus im autonomen Fahrsystem Objekte in der Umgebung, einschließlich ihrer Standorte, genau wahrnehmen und beschreiben kann.
 Das Stable Diffusion 3-Papier wird endlich veröffentlicht und die architektonischen Details werden enthüllt. Wird es helfen, Sora zu reproduzieren?
Mar 06, 2024 pm 05:34 PM
Das Stable Diffusion 3-Papier wird endlich veröffentlicht und die architektonischen Details werden enthüllt. Wird es helfen, Sora zu reproduzieren?
Mar 06, 2024 pm 05:34 PM
Der Artikel von StableDiffusion3 ist endlich da! Dieses Modell wurde vor zwei Wochen veröffentlicht und verwendet die gleiche DiT-Architektur (DiffusionTransformer) wie Sora. Nach seiner Veröffentlichung sorgte es für großes Aufsehen. Im Vergleich zur Vorgängerversion wurde die Qualität der von StableDiffusion3 generierten Bilder erheblich verbessert. Es unterstützt jetzt Eingabeaufforderungen mit mehreren Themen, und der Textschreibeffekt wurde ebenfalls verbessert, und es werden keine verstümmelten Zeichen mehr angezeigt. StabilityAI wies darauf hin, dass es sich bei StableDiffusion3 um eine Reihe von Modellen mit Parametergrößen von 800 M bis 8 B handelt. Durch diesen Parameterbereich kann das Modell direkt auf vielen tragbaren Geräten ausgeführt werden, wodurch der Einsatz von KI deutlich reduziert wird
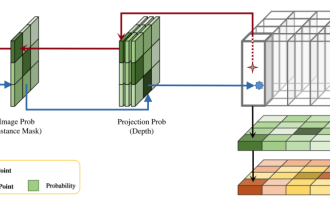 DualBEV: BEVFormer und BEVDet4D deutlich übertreffen, öffnen Sie das Buch!
Mar 21, 2024 pm 05:21 PM
DualBEV: BEVFormer und BEVDet4D deutlich übertreffen, öffnen Sie das Buch!
Mar 21, 2024 pm 05:21 PM
In diesem Artikel wird das Problem der genauen Erkennung von Objekten aus verschiedenen Blickwinkeln (z. B. Perspektive und Vogelperspektive) beim autonomen Fahren untersucht, insbesondere wie die Transformation von Merkmalen aus der Perspektive (PV) in den Raum aus der Vogelperspektive (BEV) effektiv ist implementiert über das Modul Visual Transformation (VT). Bestehende Methoden lassen sich grob in zwei Strategien unterteilen: 2D-zu-3D- und 3D-zu-2D-Konvertierung. 2D-zu-3D-Methoden verbessern dichte 2D-Merkmale durch die Vorhersage von Tiefenwahrscheinlichkeiten, aber die inhärente Unsicherheit von Tiefenvorhersagen, insbesondere in entfernten Regionen, kann zu Ungenauigkeiten führen. Während 3D-zu-2D-Methoden normalerweise 3D-Abfragen verwenden, um 2D-Features abzutasten und die Aufmerksamkeitsgewichte der Korrespondenz zwischen 3D- und 2D-Features über einen Transformer zu lernen, erhöht sich die Rechen- und Bereitstellungszeit.
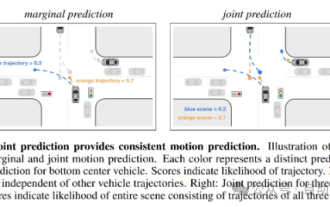
 SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
SIMPL: Ein einfacher und effizienter Multi-Agent-Benchmark zur Bewegungsvorhersage für autonomes Fahren
Feb 20, 2024 am 11:48 AM
Originaltitel: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Paper-Link: https://arxiv.org/pdf/2402.02519.pdf Code-Link: https://github.com/HKUST-Aerial-Robotics/SIMPL Autor: Hong Kong University of Science und Technologie DJI-Papieridee: Dieses Papier schlägt eine einfache und effiziente Bewegungsvorhersagebasislinie (SIMPL) für autonome Fahrzeuge vor. Im Vergleich zum herkömmlichen Agent-Cent
 FisheyeDetNet: der erste Zielerkennungsalgorithmus basierend auf einer Fischaugenkamera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: der erste Zielerkennungsalgorithmus basierend auf einer Fischaugenkamera
Apr 26, 2024 am 11:37 AM
Die Zielerkennung ist ein relativ ausgereiftes Problem in autonomen Fahrsystemen, wobei die Fußgängererkennung einer der ersten Algorithmen ist, die eingesetzt werden. In den meisten Arbeiten wurde eine sehr umfassende Recherche durchgeführt. Die Entfernungswahrnehmung mithilfe von Fischaugenkameras für die Rundumsicht ist jedoch relativ wenig untersucht. Aufgrund der großen radialen Verzerrung ist es schwierig, die standardmäßige Bounding-Box-Darstellung in Fischaugenkameras zu implementieren. Um die obige Beschreibung zu vereinfachen, untersuchen wir erweiterte Begrenzungsrahmen-, Ellipsen- und allgemeine Polygondesigns in Polar-/Winkeldarstellungen und definieren eine mIOU-Metrik für die Instanzsegmentierung, um diese Darstellungen zu analysieren. Das vorgeschlagene Modell „fisheyeDetNet“ mit polygonaler Form übertrifft andere Modelle und erreicht gleichzeitig 49,5 % mAP auf dem Valeo-Fisheye-Kameradatensatz für autonomes Fahren
 Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
Dieser Artikel reicht aus, um etwas über autonomes Fahren und Flugbahnvorhersage zu lesen!
Feb 28, 2024 pm 07:20 PM
Die Trajektorienvorhersage spielt eine wichtige Rolle beim autonomen Fahren. Unter autonomer Fahrtrajektorienvorhersage versteht man die Vorhersage der zukünftigen Fahrtrajektorie des Fahrzeugs durch die Analyse verschiedener Daten während des Fahrvorgangs. Als Kernmodul des autonomen Fahrens ist die Qualität der Trajektorienvorhersage von entscheidender Bedeutung für die nachgelagerte Planungssteuerung. Die Trajektorienvorhersageaufgabe verfügt über einen umfangreichen Technologie-Stack und erfordert Vertrautheit mit der dynamischen/statischen Wahrnehmung des autonomen Fahrens, hochpräzisen Karten, Fahrspurlinien, Fähigkeiten in der neuronalen Netzwerkarchitektur (CNN&GNN&Transformer) usw. Der Einstieg ist sehr schwierig! Viele Fans hoffen, so schnell wie möglich mit der Flugbahnvorhersage beginnen zu können und Fallstricke zu vermeiden. Heute werde ich eine Bestandsaufnahme einiger häufiger Probleme und einführender Lernmethoden für die Flugbahnvorhersage machen! Einführungsbezogenes Wissen 1. Sind die Vorschaupapiere in Ordnung? A: Schauen Sie sich zuerst die Umfrage an, S



