Hierarchisches Clustering in einem Artikel verstehen (Python-Code)

Zuallererst gehört Clustering zum unbeaufsichtigten Lernen des maschinellen Lernens, und es gibt viele Methoden, wie zum Beispiel die bekannten K-Mittel. Hierarchisches Clustering ist ebenfalls eine Form des Clusterings und wird ebenfalls sehr häufig verwendet. Als Nächstes werde ich kurz auf die Grundprinzipien von K-Means eingehen und dann langsam die Definition und die hierarchischen Schritte des hierarchischen Clusterings vorstellen, die für alle verständlicher sind.

Was ist der Unterschied zwischen hierarchischem Clustering und K-Means? Das

K-Means-Arbeitsprinzip kann kurz zusammengefasst werden als:

• Bestimmen Sie die Anzahl der Cluster (k)
• Wählen Sie zufällig k Punkte aus den Daten als Schwerpunkte aus
• Weisen Sie alle Punkte dem nächstgelegenen Clusterschwerpunkt zu
• Berechnen Sie den neuen Bildung Der Schwerpunkt des Clusters
• Wiederholen Sie die Schritte 3 und 4

Dies ist ein iterativer Prozess, bis sich der Schwerpunkt des neu gebildeten Clusters nicht ändert oder die maximale Anzahl von Iterationen erreicht ist.

Aber K-means hat einige Mängel. Wir müssen die Anzahl der Cluster K festlegen, bevor der Algorithmus startet. Wir wissen jedoch nicht, wie viele Cluster es geben sollten, daher legen wir normalerweise einen Wert fest. Dies kann zu Abweichungen zwischen unserem Verständnis und der tatsächlichen Situation führen.

Hierarchisches Clustering ist völlig anders. Es ist nicht erforderlich, dass wir zu Beginn die Anzahl der Cluster angeben. Stattdessen kann die entsprechende Anzahl von Clustern und Clustern automatisch ermittelt werden, indem der entsprechende Abstand ermittelt wird .

Was ist hierarchisches Clustering?

Jetzt stellen wir vor, was hierarchisches Clustering von flach nach tief ist.

Angenommen, wir haben die folgenden Punkte und möchten sie gruppieren:

Wir können jeden dieser Punkte einem separaten Cluster, also 4 Clustern (4 Farben), zuordnen:

Dann basierend auf dem Bei der Ähnlichkeit (Abstand) dieser Cluster werden die ähnlichsten (nächsten) Punkte gruppiert und der Vorgang wiederholt, bis nur noch ein Cluster übrig bleibt:

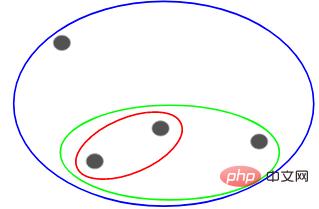
Das Obige baut im Wesentlichen eine Hierarchiestruktur auf. Lassen Sie uns dies zunächst verstehen und später die Schichtungsschritte im Detail vorstellen.

Arten von hierarchischem Clustering

Es gibt hauptsächlich zwei Arten von hierarchischem Clustering:

• Agglomeratives hierarchisches Clustering
• Geteiltes hierarchisches Clustering

Agglomeratives hierarchisches Clustering

Lassen Sie zunächst alle Punkte zu einem separaten Cluster werden. Anschließend werden sie durch Ähnlichkeit kontinuierlich kombiniert bis es am Ende nur noch einen Cluster gibt. Dies ist der Prozess der agglomerativen hierarchischen Clusterbildung, der mit dem übereinstimmt, was wir oben gesagt haben.

Geteiltes hierarchisches Clustering

Geteiltes hierarchisches Clustering ist genau das Gegenteil. Es beginnt mit einem einzelnen Cluster und teilt ihn schrittweise auf, bis er nicht mehr geteilt werden kann, dh jeder Punkt ist ein Cluster.

Es spielt also keine Rolle, ob Sie 10, 100, 1000 Datenpunkte haben, diese Punkte gehören zu Beginn alle zum selben Cluster:

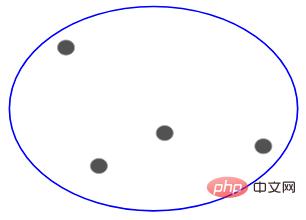
Jetzt teilen Sie in jeder Iteration die beiden am weitesten voneinander entfernten Clusterpunkte auf, und wiederholen Sie diesen Vorgang, bis jeder Cluster nur noch einen Punkt enthält:

Der obige Prozess ist geteiltes hierarchisches Clustering.

Schritte zur Durchführung des hierarchischen Clusterings

Der allgemeine Prozess des hierarchischen Clusterings wurde oben beschrieben. Nun kommt der entscheidende Punkt.

Dies ist eines der wichtigsten Probleme beim Clustering. Die allgemeine Methode zur Berechnung der Ähnlichkeit besteht darin, den Abstand zwischen den Schwerpunkten dieser Cluster zu berechnen. Die Punkte mit minimalem Abstand werden als ähnliche Punkte bezeichnet und wir können sie zusammenführen oder es als abstandsbasierten Algorithmus bezeichnen.

Auch beim hierarchischen Clustering gibt es ein Konzept namens Proximity-Matrix, das den Abstand zwischen jedem Punkt speichert. Nachfolgend verwenden wir ein Beispiel, um zu verstehen, wie Ähnlichkeit, Näherungsmatrix und die spezifischen Schritte der hierarchischen Clusterbildung berechnet werden.

Falleinführung

Angenommen, ein Lehrer möchte Schüler in verschiedene Gruppen einteilen. Jetzt habe ich die Ergebnisse jedes Schülers für die Aufgabe und möchte sie anhand dieser Ergebnisse in Gruppen einteilen. Hier gibt es kein festgelegtes Ziel, wie viele Gruppen es geben soll. Da der Lehrer nicht weiß, welcher Schülertyp welcher Gruppe zuzuordnen ist, kann es nicht als überwachtes Lernproblem gelöst werden. Im Folgenden werden wir versuchen, hierarchisches Clustering anzuwenden, um Schüler in verschiedene Gruppen zu unterteilen.

Das Folgende sind die Ergebnisse von 5 Schülern:

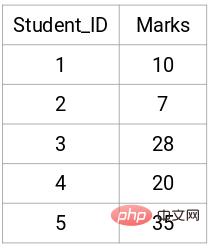
Erstellen Sie eine Näherungsmatrix.

Zuerst müssen wir eine Näherungsmatrix erstellen, die den Abstand zwischen den einzelnen Punkten speichert, sodass wir eine quadratische Matrix mit der Form n x n erhalten können.

In diesem Fall kann die folgende 5 x 5-Proximity-Matrix erhalten werden:

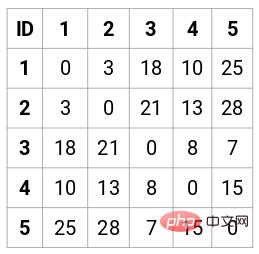
In der Matrix sind zwei Punkte zu beachten:

• Die Diagonalelemente der Matrix sind immer 0, da der Abstand zwischen a Punkt und sich selbst sind immer 0
• Verwenden Sie die euklidische Abstandsformel, um den Abstand nichtdiagonaler Elemente zu berechnen. Wenn wir beispielsweise den Abstand zwischen den Punkten 1 und 2 berechnen möchten, lautet die Berechnungsformel:

Berechnen Sie es auf ähnliche Weise wie folgt. Nach Abschluss der Methode werden die verbleibenden Elemente der Näherungsmatrix gefüllt.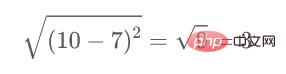

Hierarchisches Clustering durchführen

Dies wird durch agglomeratives hierarchisches Clustering implementiert.

Schritt 1: Zuerst ordnen wir alle Punkte einem einzigen Cluster zu:

Hier stellen verschiedene Farben unterschiedliche Cluster dar, 5 Punkte in unseren Daten, das heißt, es gibt 5 verschiedene Cluster.

Schritt 2: Als nächstes müssen wir den Mindestabstand in der Nähematrix ermitteln und die Punkte mit dem kleinsten Abstand zusammenführen. Dann aktualisieren wir die Näherungsmatrix:

Der Mindestabstand beträgt 3, also werden wir die Punkte 1 und 2 zusammenführen: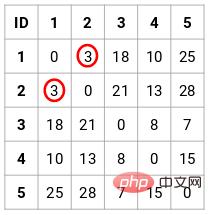

Sehen wir uns die aktualisierten Cluster an und aktualisieren wir die Näherungsmatrix entsprechend: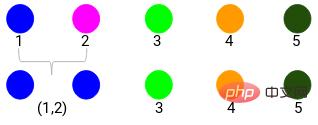

Aktualisieren Danach haben wir den größten Wert (7, 10) zwischen den Punkten 1 und 2 genommen, um den Wert dieses Clusters zu ersetzen. Natürlich können wir neben dem Maximalwert auch den Minimal- oder Durchschnittswert annehmen. Anschließend berechnen wir erneut die Proximity-Matrix dieser Cluster: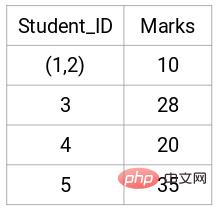

Schritt 3: Wiederholen Sie Schritt 2, bis nur noch ein Cluster übrig ist.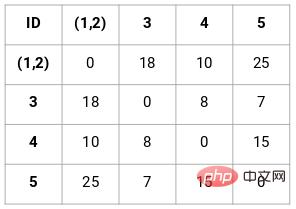

Nachdem wir alle Schritte wiederholt haben, erhalten wir die zusammengeführten Cluster wie unten gezeigt:

So funktioniert agglomeratives hierarchisches Clustering. Aber das Problem ist, dass wir immer noch nicht wissen, in wie viele Gruppen wir uns aufteilen sollen? Ist es Gruppe 2, 3 oder 4?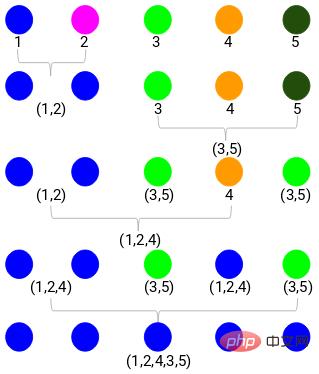

Beginnen wir mit der Auswahl der Anzahl der Cluster.

Wie wähle ich die Anzahl der Cluster aus?

Um die Anzahl der Cluster für die hierarchische Clusterbildung zu ermitteln, verwenden wir ein Konzept namens Dendrogramm.

Durch das Dendrogramm können wir die Anzahl der Cluster einfacher auswählen.

Zurück zum obigen Beispiel. Wenn wir zwei Cluster zusammenführen, erfasst das Dendrogramm entsprechend den Abstand zwischen diesen Clustern und stellt ihn grafisch dar. Das Folgende ist der ursprüngliche Zustand des Dendrogramms. Die Abszisse zeichnet die Markierung jedes Punkts auf, und die vertikale Achse zeichnet den Abstand zwischen den Punkten auf:

Beim Zusammenführen von zwei Clustern wird das Dendrogramm angezeigt Verbindung ist der Abstand zwischen den Punkten. Das Folgende ist der Prozess der hierarchischen Clusterbildung, den wir gerade durchgeführt haben.

Dann beginnen Sie mit dem Zeichnen eines Baumdiagramms des obigen Prozesses. Ausgehend von der Zusammenführung der Proben 1 und 2 beträgt der Abstand zwischen diesen beiden Proben 3.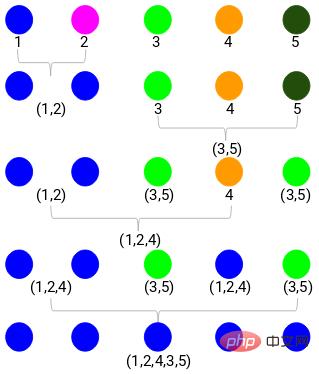

Sie können sehen, dass 1 und 2 zusammengeführt wurden. Die vertikale Linie stellt den Abstand zwischen 1 und 2 dar. Auf die gleiche Weise werden alle Schritte zum Zusammenführen von Clustern gemäß dem hierarchischen Clustering-Prozess gezeichnet und schließlich ein Dendrogramm wie dieses erhalten: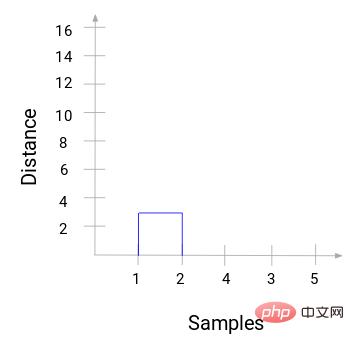

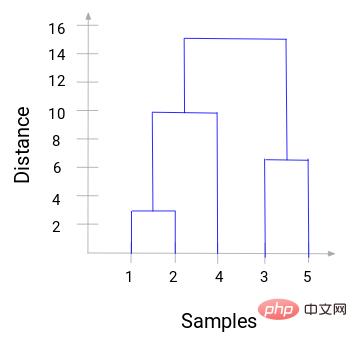
Durch das Dendrogramm können wir die Schritte der hierarchischen Clusterbildung klar visualisieren. Je weiter die vertikalen Linien im Dendrogramm voneinander entfernt sind, desto größer ist der Abstand zwischen den Clustern.

Mit diesem Dendrogramm ist es für uns viel einfacher, die Anzahl der Cluster zu bestimmen.

Jetzt können wir einen Schwellenwertabstand festlegen und eine horizontale Linie zeichnen. Zum Beispiel setzen wir den Schwellenwert auf 12 und zeichnen eine horizontale Linie wie folgt:

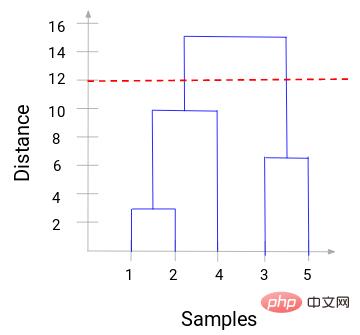
Wie Sie an den Schnittpunkten sehen können, ist die Anzahl der Cluster die Anzahl der Schnittpunkte mit der horizontalen Schwellenlinie und der vertikalen Linie (die (rote Linie schneidet zwei vertikale Linien, wir werden zwei Cluster haben). Entsprechend der Abszisse verfügt ein Cluster über einen Stichprobensatz (1,2,4) und der andere Cluster über einen Stichprobensatz (3,5).

Auf diese Weise lösen wir das Problem der Bestimmung der Anzahl der Cluster in der hierarchischen Clusterbildung durch ein Dendrogramm.

Praktischer Fall von Python-Code

Das Obige ist die theoretische Grundlage, und jeder mit einigen mathematischen Grundlagen kann es verstehen. Hier erfahren Sie, wie Sie diesen Prozess mit Python-Code implementieren. Hier sind Kundensegmentierungsdaten zu sehen.

Der Datensatz und der Code befinden sich in meinem GitHub-Repository:

​​https://github.com/xiaoyusmd/PythonDataScience​​

Wenn Sie es hilfreich finden, geben Sie ihm bitte einen Stern!

Diese Daten stammen aus der UCI-Bibliothek für maschinelles Lernen. Unser Ziel ist es, die Kunden von Großhändlern anhand ihrer jährlichen Ausgaben für verschiedene Produktkategorien (z. B. Milch, Lebensmittel, Regionen usw.) zu segmentieren.

Standardisieren Sie zunächst die Daten, um alle Daten in derselben Dimension einfach zu berechnen, und wenden Sie dann hierarchisches Clustering an, um Kunden zu segmentieren.

from sklearn.preprocessing import normalize
data_scaled = normalize(data)
data_scaled = pd.DataFrame(data_scaled, columns=data.columns)
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Dendrograms")
dend = shc.dendrogram(shc.linkage(data_scaled, method='ward'))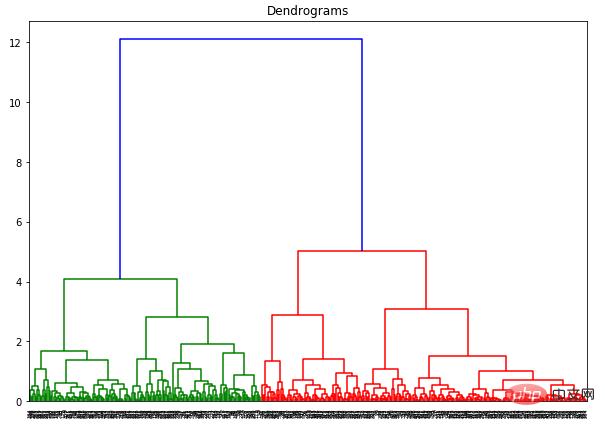

Die x-Achse enthält alle Proben und die y-Achse stellt den Abstand zwischen diesen Proben dar. Die vertikale Linie mit dem größten Abstand ist die blaue Linie. Angenommen, wir beschließen, das Dendrogramm mit einem Schwellenwert von 6 zu schneiden:

plt.figure(figsize=(10, 7))
plt.title("Dendrograms")
dend = shc.dendrogram(shc.linkage(data_scaled, method='ward'))
plt.axhline(y=6, color='r', linestyle='--')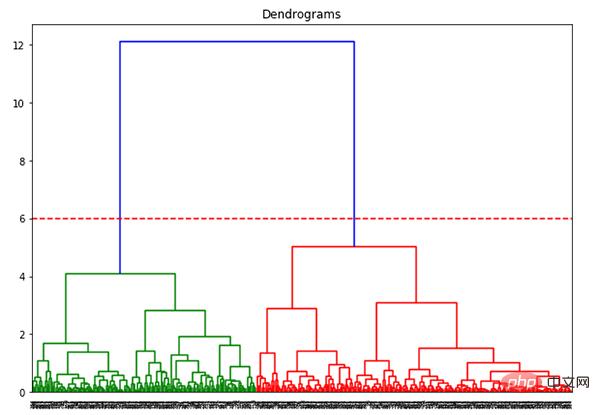

Da wir nun zwei Cluster haben, möchten wir hierarchisches Clustering auf diese beiden Cluster anwenden:

from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(data_scaled)

Da wir 2 Cluster definiert haben, können wir in der Ausgabe die Werte 0 und 1 sehen. 0 stellt Punkte dar, die zum ersten Cluster gehören, und 1 stellt Punkte dar, die zum zweiten Cluster gehören.

plt.figure(figsize=(10, 7))
plt.scatter(data_scaled['Milk'], data_scaled['Grocery'], c=cluster.labels_)

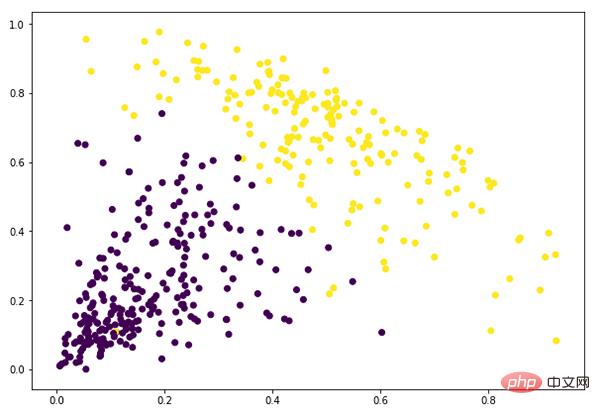
An diesem Punkt haben wir das Clustering erfolgreich abgeschlossen.

Das obige ist der detaillierte Inhalt vonHierarchisches Clustering in einem Artikel verstehen (Python-Code). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!