Kontrolle ist die Strategie, die das Fahrzeug vorantreibt. Ziel der Regelung ist es, mit realisierbaren Regelgrößen Abweichungen von der Soll-Trajektorie zu minimieren, den Fahrgastkomfort zu maximieren etc.
Wie in der Abbildung oben gezeigt, umfassen die mit der Eingabe des Steuermoduls verbundenen Module Planungsmodul, Positionierungsmodul und Fahrzeuginformationen usw. Das Positionierungsmodul liefert Informationen zum Fahrzeugstandort, das Planungsmodul liefert Informationen zur Zielbahn und zu den Fahrzeuginformationen gehören Gang, Geschwindigkeit, Beschleunigung usw. Die Steuerausgänge sind Lenk-, Beschleunigungs- und Bremsgrößen.
Das Steuermodul ist hauptsächlich in horizontale Steuerung und vertikale Steuerung unterteilt. Je nach Kopplungsform kann es in zwei Methoden unterteilt werden: unabhängig und integriert.
Die sogenannte Entkopplungssteuerung bedeutet, die horizontalen und vertikalen Steuerungsmethoden unabhängig voneinander zu steuern.
Die Kopplungssteuerung berücksichtigt die Kopplungsprobleme, die bei der horizontalen und vertikalen Steuerung bestehen. Ein typisches Beispiel ist, dass ein Auto nicht mit hoher Geschwindigkeit kurven fahren kann, da bei zu hoher Längsgeschwindigkeit die seitliche Winkelgeschwindigkeit begrenzt werden muss, da sonst die Zentripetalkraft die Zentripetalbeschleunigung nicht befriedigen kann.
Die typische repräsentative Methode der horizontalen und vertikalen Integration ist die lineare zeitvariable modellprädiktive Steuerung. Diese Methode fügt horizontale und vertikale Gelenkbeschränkungen auf der Grundlage der modellprädiktiven Steuerung hinzu. Wie maximale Zentripetalbeschleunigungsbeschränkungen usw.
Wie in der Abbildung oben gezeigt, kann die Querkontrolle in geometrische Methoden, kinematische modellbasierte Methoden und dynamische modellbasierte Methoden unterteilt werden.
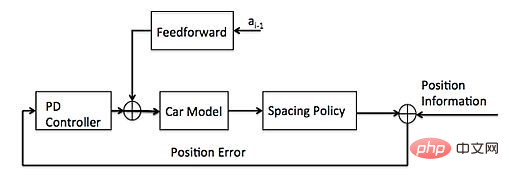
Die sogenannte Feedforward-Steuerung bedeutet, den Steuerbetrag im Voraus basierend auf den Tracking-Point-Informationen angemessen zu kompensieren. Ein typisches Beispiel ist die Verwendung der Krümmungsinformationen in den Tracking-Sequenzpunkten, um den Drehwinkel zu kompensieren.
Das verkettete System führt eine mehrschichtige Linearisierung des nichtlinearen Systems durch. Es zerlegt das System Schicht für Schicht und kann das System beschleunigen, ähnlich wie das Filtersystem [3].
Das Modell des Systems in Frenet-Koordinaten:
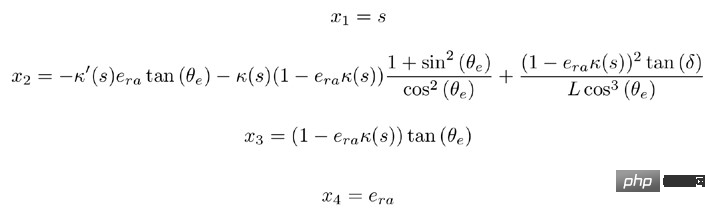
Nach dem umgekehrten Integralbudget kann die Kontrollrate erhalten werden:
Basierend auf Li Yap. Der Entwurf der Nove-Stabilitätsmethode kann auf kinematische und dynamische Modelle angewendet werden. Die Grundidee besteht darin, zunächst ein kinematisches oder dynamisches Modell zu erstellen, eine auf dem Modell basierende Verfolgungsmethode vorzuschlagen und dann eine Lyapunov-Funktion zu erstellen, um die asymptotische Stabilität des Systems mit geschlossenem Regelkreis durch Lyapunov-Stabilität zu beweisen [4].
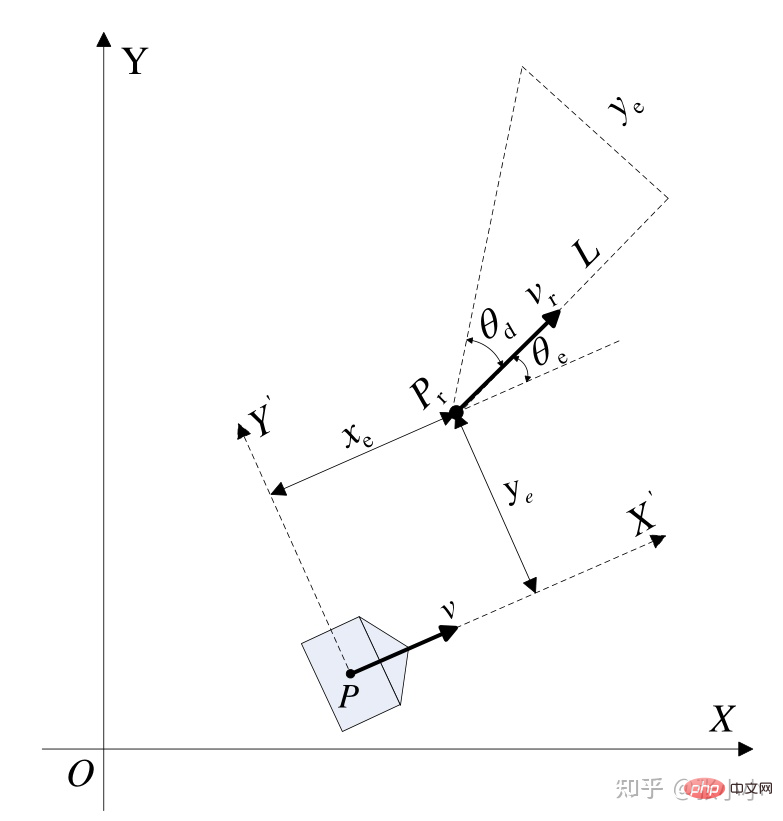
Wie in der Abbildung oben gezeigt, ist der aktuelle Punkt des Fahrzeugs P und der Tracking-Zielpunkt Pr. ist die Posendifferenz zwischen der aktuellen Position und dem Zielpunkt und sind die Referenzgeschwindigkeit bzw. Winkelgeschwindigkeit. Entwerfen Sie die Lyapunov-Funktion:
Tracking-Rate-Design:
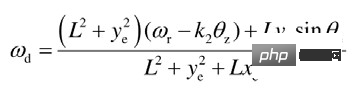
Schließlich wird durch Begrenzen der Einschränkungsdesignparameter die asymptotische Stabilität der Tracking-Rate bewiesen, d. h. wenn → ∞, → 0 .
Erstellen Sie zunächst das kinetische Modell:
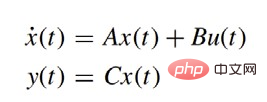
wobei:
Reihenfolge
Dann ist der Fehler:
Designkostenfunktion:
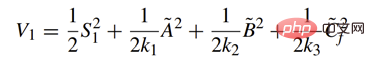
Designkontrollrate:
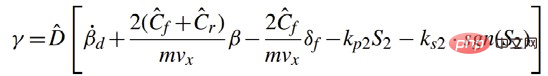
Beweisen Sie abschließend die asymptotische Stabilität.
Pure Tracking ist ein geometrischer Pfadverfolgungscontroller. Dieser Controller nutzt die geometrische Beziehung zwischen der Fahrzeugbewegung und dem Referenzpfad, um den Controller des Referenzpfads zu verfolgen. Bei dieser Steuermethode wird die Mitte der Hinterachse des Fahrzeugs als Referenzpunkt verwendet.
Gemäß der obigen Abbildung kann der Vorderradwinkelbefehl abgeleitet werden:
wobei R der Wenderadius, L der Radstand des Fahrzeugs und e die aktuelle Fluglage ist des Fahrzeugs und des Zielwegpunkts in seitlicher Richtung. Der Fehler von ist die Sichtweite nach vorne und .
Gemäß den experimentellen Daten in der obigen Abbildung wird der Tracking-Jitter mit zunehmender Vorwärtsentfernung immer kleiner. Ein kürzerer Visierabstand sorgt für eine präzisere Verfolgung, während ein größerer Visierabstand für eine gleichmäßigere Verfolgung sorgt. Ein weiteres Merkmal des PurePursuit ist, dass ein zu großer Visierabstand beim Verfolgen von Kurven zu „Abbiegen“ führen kann. Der Pure Pursuit ist ein harter Kompromiss zwischen Stabilität und Tracking-Leistung.
Im Gegensatz zur reinen Verfolgungs- und Verfolgungsmethode, bei der die hintere Achse als Referenzpunkt verwendet wird, verwendet der Stanley-Controller die vordere Achse als Referenzpunkt. Es berücksichtigt sowohl Kurs- als auch Seitenfehler. Der Stanley-Controller berücksichtigt nicht nur Kursfehler, sondern auch seitliche Fehler.
Gemäß der obigen Abbildung kann der Vorderradwinkelbefehl abgeleitet werden:
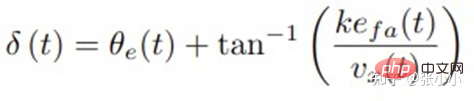
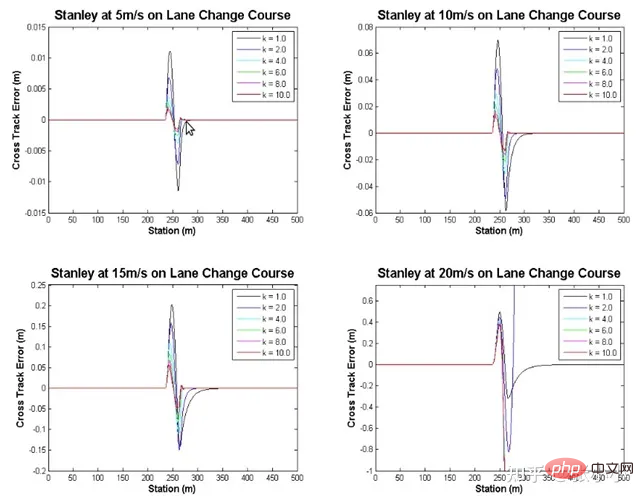
Gemäß den experimentellen Daten in der obigen Abbildung erhöht sich die Trackingleistung mit zunehmendem k auch verbessern. Stanley verfügt nicht über genügend Stabilität wie Pure Pursuit, wenn die Fahrzeuggeschwindigkeit zunimmt.
Die auf dem Fahrzeugkinematikmodell basierende Methode ignoriert die dynamischen Eigenschaften des Fahrzeugs, sodass der Algorithmus die Stabilitätskontrolle des Fahrzeugs nicht erfüllen kann, wenn die Fahrzeuggeschwindigkeit zu hoch ist oder sich die Krümmung ändert Rate ist zu groß. Bei auf Fahrdynamikmodellen basierenden Regelungsverfahren besteht die primäre Aufgabe darin, die Fahrzeugdynamik zu modellieren. Da das genaue dynamische Modell mit zwei Freiheitsgraden nichtlinear ist, ist es zur Erleichterung von Echtzeit-Tracking-Steuerungsberechnungen normalerweise erforderlich, einige vereinfachte Näherungen auf der Grundlage des zu erhaltenden genauen dynamischen Modells mit zwei Freiheitsgraden vorzunehmen ein lineares dynamisches Modell mit zwei Freiheitsgraden.
Der lineare quadratische Regler (LQR) ist ein Modellbasierter Controller, der verwendet den Zustand des Fahrzeugs, um den Fehler zu minimieren. Die LQR-Theorie ist die früheste und ausgereifteste Methode zur Zustandsraumgestaltung in der modernen Kontrolltheorie. LQR kann das optimale Steuergesetz der linearen Zustandsrückkopplung erhalten und ist einfach, eine optimale Regelung mit geschlossenem Regelkreis zu bilden.
LQR-optimales Design bedeutet, dass der entworfene Zustandsrückkopplungsregler K die quadratische Zielfunktion J minimieren sollte und K eindeutig durch die Gewichtsmatrizen Q und R bestimmt wird, sodass die Auswahl von Q und R besonders wichtig ist. Die folgende Formel ist die LQR-Kostenfunktion:
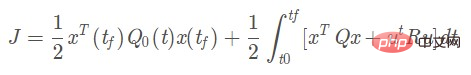
Anhand des Fahrzeugdynamikmodells und der LQR-Kostenfunktion kann die algebraische Riccati-Gleichung abgeleitet werden:
Schließlich lautet die Rückkopplungsmatrix Berechnet durch die iterative Riccati-Gleichung und erhält dann den optimalen Kontrollbetrag gemäß der Rückkopplungsmatrix.
MPC (Model Prediction Control) ist eine Art Optimierungskontrollproblem, das sich der Zerlegung längerer Zeitspannen oder sogar unendlicher Zeitspannen in mehrere kürzere Zeitspannen oder endliche Zeitspannen widmet Problem in der Zeitspanne zu erkennen und dennoch bis zu einem gewissen Grad die optimale Lösung zu verfolgen.
MPC besteht aus den folgenden drei Elementen:
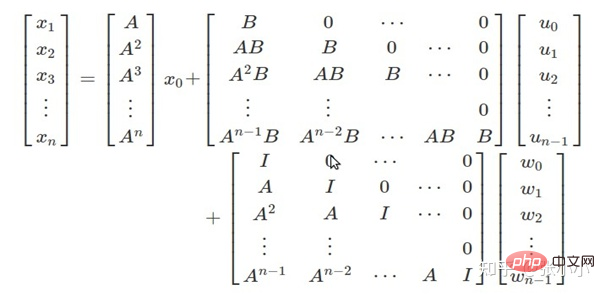
Rolloptimierung:
Basierend auf dem Vorhersagemodell, den seitlichen Fahrzeugbeschränkungen und der entsprechenden Kostenfunktion Steueranweisungen können sein erhalten durch Optimierung und Lösung.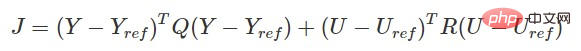 
1.3.8 Vergleich horizontaler Steuerungsalgorithmen
1.4 Vertikal 
Wie in der Abbildung oben gezeigt, verwendet die vertikale Steuerung im Allgemeinen die Kaskaden-PID-Steuerungsmethode.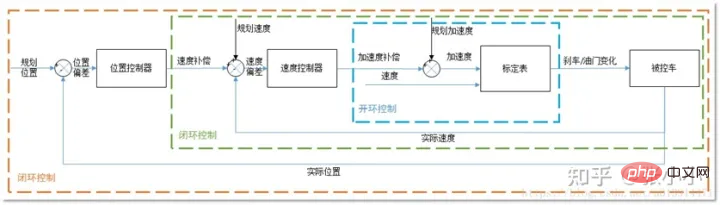 
2 Detailliertes Design
Das Design des Controllers ist wie in der Abbildung oben dargestellt, wobei Controller die Basisklasse ist und LonController, LonController und MPCController diese Basisklasse erben. LonController hat abgeleitete Unterklassen wie LQRController, LyapunovController und StanleyController.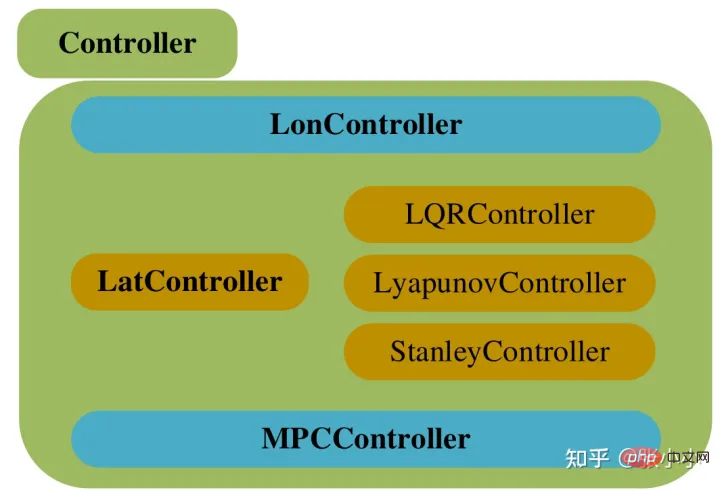 
Das obige ist der detaillierte Inhalt vonAusführliche Erläuterung häufig verwendeter Steuerungsmethoden für die Planung und Steuerung intelligenter Autos. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
