
GNN ist in den letzten Jahren ein sehr beliebtes Feld. Kürzlich wurde in einer Fachzeitschrift von Nature eine Methode zur Verwendung von GNN zur Lösung kombinatorischer Optimierungsprobleme vorgeschlagen und behauptet, dass die Leistung des GNN-Optimierers der Leistung bestehender Löser entspricht oder diese sogar übertrifft. Dieses Papier hat jedoch einige Zweifel geweckt: Einige Leute wiesen darauf hin, dass die Leistung dieses GNN tatsächlich nicht so gut ist wie die des klassischen Greedy-Algorithmus und die Geschwindigkeit viel langsamer ist als die des Greedy-Algorithmus (bei Problemen mit einer Million Variablen der Greedy-Algorithmus). Der Algorithmus ist besser als das GNN (104-mal schneller). Daher sagten die Skeptiker: „Wir sehen keinen guten Grund, diese GNNs zur Lösung dieses Problems zu verwenden, es ist, als würde man mit einem Vorschlaghammer Nüsse knacken.“ Sie hoffen, dass die Autoren dieser Papiere zunächst das schwierige Problem lösen können, bevor sie das behaupten.“ Überlegenheit der Methode. Vergleichen Sie die Benchmarks.
Neuronale Netze haben in den letzten Jahren viele schwierige Probleme in der Anwendung und Grundlagenwissenschaft gelöst, darunter auch diskrete kombinatorische Optimierungsprobleme, die auch die Grundlage für unser Verständnis der Grenzen des Rechnens bilden.
Die Studie von Martin JA Schuetz et al. aus dem Jahr 2022 „Kombinatorische Optimierung mit physikinspirierten graphischen neuronalen Netzen“ [4] schlägt vor, physikinspirierte unbeaufsichtigte graphische neuronale Netze (GNN) zu verwenden, um kombinatorische Optimierungsprobleme auf Graphen zu lösen Der Ansatz erscheint vielversprechend und wurde in einer renommierten Fachzeitschrift (Nature Machine Intelligence) veröffentlicht. Die Studie testete die Leistung von GNNs bei zwei Standardoptimierungsproblemen: Max-Cut und Maximal Independent Set (MIS). Dieser neu vorgeschlagene GNN-Optimierer hat eine sehr schöne Eigenschaft: Er kann auf viele größere Instanzprobleme erweitert werden. 🎙 „Klassische gierige Algorithmen“ stellten die Forschung von Martin JA Schütz et al. in Frage und glaubten, dass der von Martin JA Schütz et al. vorgeschlagene GNN-Optimierer „Nüsse mit einem Vorschlaghammer knackt, ähnlich wie das Schlagen von Mücken mit einem Mörser“, was eine Verschwendung ist Ressourcenverbrauch und schlechte Ergebnisse.

Papieradresse: https://arxiv.org/abs/2206.13211
MIS Das Problem ist wie folgt definiert: Gegeben sei ein ungerichteter Zufallsregulärer mit n Knoten und festem Grad d Graph (d -RRG) bezieht sich die unabhängige Menge (IS) auf die Teilmenge der Eckpunkte, die keine nächsten Nachbarpaare enthält. Das MIS-Problem erfordert die Suche nach der größten IS, deren Größe α genannt wird. MIS ist ein NP-schweres Problem, aber man möchte einen Algorithmus finden, um ein IS mit einer Größe zu finden, die in polynomieller Zeit möglichst nahe am Maximum liegt. Darüber hinaus sollte ein guter Algorithmus bei größeren Werten von n keine Leistungseinbußen erleiden.
Das von Martin JA Schuetz et al. vorgeschlagene neue GNN kann IS für sehr große Graphen finden (n≤ 10^6): Die Laufzeit des Algorithmus ist proportional zur Problemgröße: t∼ n^1,7 und der Algorithmus Die Leistung steigt mit n. Der Anstieg bleibt stabil, wie in Abbildung 1 unten dargestellt. 
Beim Vergleich der Leistung des vorgeschlagenen GNN mit anderen verfügbaren Algorithmen verglich die Studie es jedoch nur mit dem Boppana-Halldorsson (BH)-Näherungsalgorithmus [8], der verwendet wird, wenn n≤ Bei 500 beträgt die Laufzeit t∼n^2,9.
Es gibt tatsächlich viele andere Algorithmen zur Berechnung von IS, die viel schneller sind als BH, und die Studie sollte den vorgeschlagenen GNN-Optimierer mit diesen Algorithmen vergleichen. Unter ihnen ist der einfachste Algorithmus der Greedy-Algorithmus (GA) [9]. Nachdem der gradbasierte Greedy-Algorithmus (DGA) optimiert wurde, ist die Laufzeit nahezu linear mit der Anzahl der Knoten n.
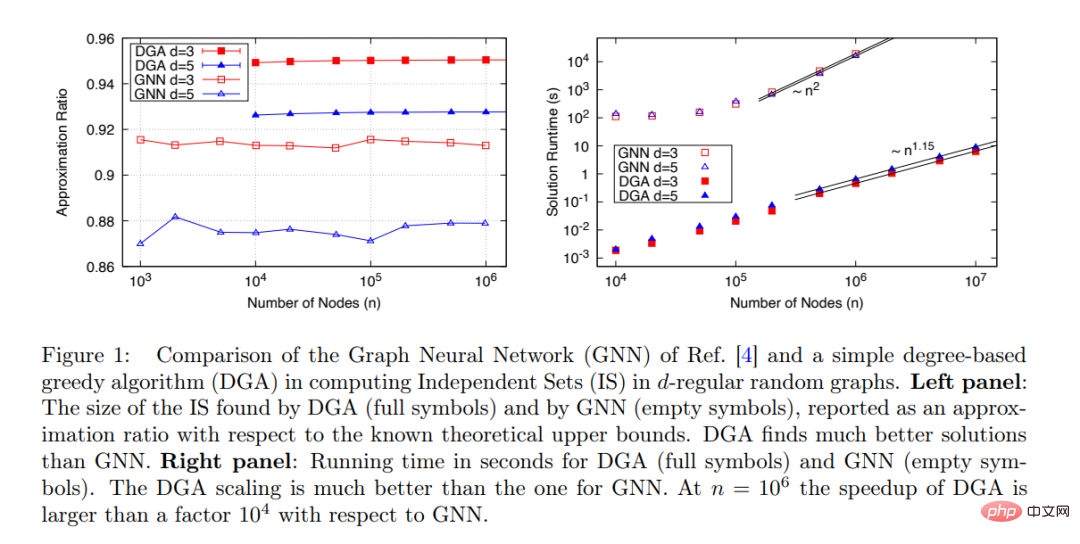 Diese Studie vergleicht die Leistung des von Martin JA Schuetz et al. vorgeschlagenen GNN-Optimierers (offen) und DGA (solid) zum Finden von MIS auf d-RRG mit d=3 und d=5.
Diese Studie vergleicht die Leistung des von Martin JA Schuetz et al. vorgeschlagenen GNN-Optimierers (offen) und DGA (solid) zum Finden von MIS auf d-RRG mit d=3 und d=5.
Diese Studie geht davon aus, dass die Behauptung von Martin JA Schuetz et al., dass „die Leistung von Optimierern, die auf graphischen neuronalen Netzen basieren, gleichwertig oder besser ist als bestehende Löser, das aktuelle SOTA-Modell übertreffen kann und erweitert werden kann.“ „Das Problem der Millionen Variablen“ kann einer genaueren Prüfung nicht standhalten und steht im Widerspruch zu den tatsächlichen experimentellen Ergebnissen. Martin JA Schütz und andere sollten das Papier überarbeiten.
Diese Studie klärt die Leistung von DGA im Detail und ist der Ansicht, dass dieser einfache Greedy-Algorithmus als Mindestmaßstab betrachtet werden sollte und die Leistung jedes neuen Algorithmus mindestens besser als die von DGA sein muss, bevor er übernommen werden kann.
Natürlich ist DGA nur ein extrem einfacher Algorithmus, und es gibt viele andere Standardalgorithmen, die besser als DGA sind. Die Arbeit von Maria Chiara et al. aus dem Jahr 2019 „Monte-Carlo-Algorithmen sind sehr effektiv bei der Suche nach der größten unabhängigen Menge in dünn besetzten Zufallsgraphen“ bietet eine eingehende Untersuchung der Leistung mehrerer Algorithmen zur Lösung von MIS-Problemen.
Auf dieser Grundlage wirft die Studie die Frage auf: „Welche wirklich schwierigen Probleme sollten bei der Bewertung eines neuen Optimierungsalgorithmus als Maßstab verwendet werden, um die Leistung des Algorithmus zu testen?“ Studie geht davon aus, dass in d 16 MIS auf d-RRG. Hier können die Ergebnisse für d=20 und d=100 mit den Ergebnissen aus der Arbeit „Monte-Carlo-Algorithmen sind sehr effektiv bei der Suche nach der größten unabhängigen Menge in dünn besetzten Zufallsgraphen“ aus dem Jahr 2019 verglichen werden.
Natürlich sollte ein guter Optimierungsalgorithmus in der Polynomzeit von n abgeschlossen werden. Es wäre besser, wenn die Qualität der gefundenen Lösung besser wäre als die einfacher bestehender Algorithmen, und sie sollte nicht zunehmen mit n. erhöht, während die Qualität abnahm.
Die Studie kam zu dem Schluss: Derzeit erfüllen auf neuronalen Netzwerken basierende Optimierer (wie die von Martin JA Schuetz et al. vorgeschlagenen) die oben genannten Anforderungen nicht und können nicht mit einfachen Standardalgorithmen konkurrieren, um schwierige Optimierungsprobleme zu lösen. Es ist von entscheidender Bedeutung zu untersuchen, ob neuronale Netze diese Anforderung erfüllen können oder ob es tiefere Gründe für ihr Scheitern gibt.
Das obige ist der detaillierte Inhalt vonDas graphische neuronale Netzwerk wurde in einer Unterzeitschrift von Nature veröffentlicht, aber es stellte sich heraus, dass es 104-mal langsamer war als der gewöhnliche Algorithmus. Fragende: Ist es eine neue Höhe?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Lösungen für unbekannte Software-Ausnahmen in Computeranwendungen
Lösungen für unbekannte Software-Ausnahmen in Computeranwendungen
 Komplementalgorithmus für negative Zahlen
Komplementalgorithmus für negative Zahlen
 Verwendung der Rowcount-Funktion
Verwendung der Rowcount-Funktion
 Datenbank-Er-Diagramm
Datenbank-Er-Diagramm
 So überprüfen Sie tote Links auf Websites
So überprüfen Sie tote Links auf Websites
 So stellen Sie aus dem Papierkorb geleerte Dateien wieder her
So stellen Sie aus dem Papierkorb geleerte Dateien wieder her
 Die Rolle der klonbaren Schnittstelle
Die Rolle der klonbaren Schnittstelle
 So verwenden Sie die magnetische Btbook-Suche
So verwenden Sie die magnetische Btbook-Suche




