 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 rollen! Das Poisson-Strömungserzeugungsmodell des MIT übertrifft das Diffusionsmodell, wenn es um Qualität und Geschwindigkeit geht
rollen! Das Poisson-Strömungserzeugungsmodell des MIT übertrifft das Diffusionsmodell, wenn es um Qualität und Geschwindigkeit geht
rollen! Das Poisson-Strömungserzeugungsmodell des MIT übertrifft das Diffusionsmodell, wenn es um Qualität und Geschwindigkeit geht
Einführung
Das Diffusionsmodell wurde ursprünglich aus der Thermodynamik in der Physik abgeleitet, erfreut sich jedoch in jüngster Zeit auch im Bereich der künstlichen Intelligenz großer Beliebtheit. Welche anderen physikalischen Theorien können die Entwicklung generativer Modellforschung fördern? Kürzlich ließen sich Forscher des MIT von der hochdimensionalen elektromagnetischen Theorie inspirieren und schlugen ein generatives Modell namens Poisson Flow vor. Theoretisch verfügt dieses Modell über intuitive Bilder und eine strenge Theorie; experimentell ist es in Bezug auf Generierungsqualität, Generierungsgeschwindigkeit und Robustheit oft besser als das Diffusionsmodell. Dieser Artikel wurde von NeurIPS 2022 angenommen.

- Papieradresse: https://arxiv.org/abs/2209.11178
- Codeadresse: https://github.com/Newbeeer/Poisson_flow
Inspiriert von der Elektrostatik s, Die Forscher schlugen ein neues generatives Modell namens Poisson-Flow-Modell (Poisson Flow Generative Models oder PFGM) vor. Intuitiv kann diese Forschung die N-dimensionalen Datenpunkte als eine Gruppe positiver Ladungen auf der z=0-Ebene betrachten, einer neuen Dimension im N+1-dimensionalen Raum. Sie erzeugen ein elektrisches Feld im hochdimensionalen Raum. Ausgehend von der z=0-Ebene und entlang der von ihnen erzeugten elektrischen Feldlinien nach außen konnte die Studie die Probe zu einer Halbkugel transportieren (wie in Abbildung 1 dargestellt). Die Richtung dieser elektrischen Feldlinien entspricht dem Gradienten der Lösung der Poisson-Gleichung im hochdimensionalen Raum. Die Forscher bewiesen, dass die elektrischen Feldlinien die Ladungsverteilung (d. h. die Datenverteilung) auf der z=0-Ebene in eine gleichmäßige Verteilung auf der Halbkugel umwandeln können, wenn der Radius der Halbkugel groß genug ist (Abbildung 2).
PFGM nutzt die Reversibilität elektrischer Feldlinien, um eine Datenverteilung auf der z=0-Ebene zu erzeugen: Zuerst nehmen die Forscher gleichmäßig Proben auf einer großen Halbkugel und lassen die Probe dann entlang der elektrischen Feldlinien von der Kugel aus wandern zur z=0-Ebene, wodurch Daten generiert werden. Da die Bewegung entlang elektrischer Feldlinien durch eine gewöhnliche Differentialgleichung (ODE) beschrieben werden kann, müssen Forscher bei der tatsächlichen Probenahme nur eine ODE lösen, die durch die Richtung der elektrischen Feldlinien bestimmt wird. Durch ein elektrisches Feld wandelt PFGM eine einfache Verteilung auf einer Kugel in eine komplexe Datenverteilung um. Aus dieser Perspektive kann PFGM als kontinuierlicher Normalisierungsfluss (Normalisierungsfluss) betrachtet werden.
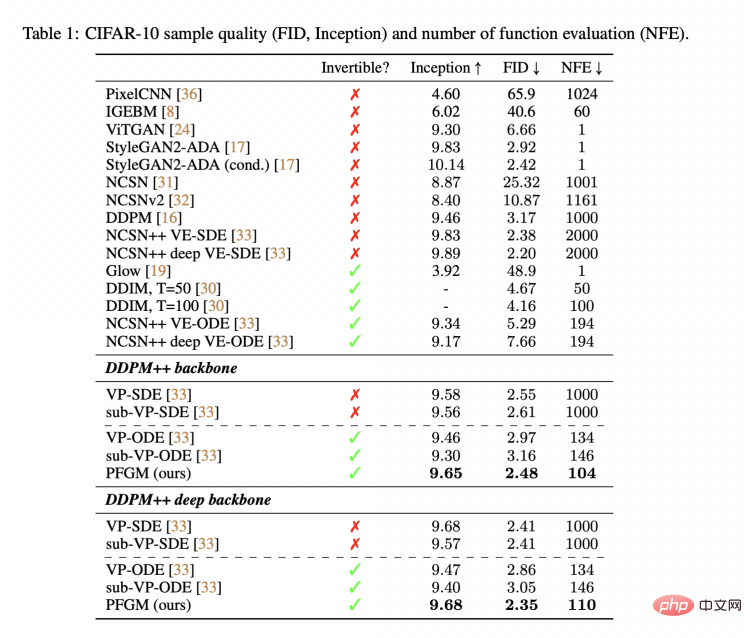
Im Bildgenerierungsexperiment ist PFGM derzeit das leistungsstärkste normalisierte Strömungsmodell auf dem Standarddatensatz CIFAR-10 und erreicht einen FID-Score (ein Maß für die Bildqualität) von 2,35. Die Forscher demonstrierten auch andere Einsatzmöglichkeiten von PFGM, etwa seine Fähigkeit, die Bildwahrscheinlichkeit zu berechnen, Bildbearbeitung durchzuführen und auf hochauflösende Bilddatensätze zu skalieren. Darüber hinaus fanden Forscher heraus, dass PFGM gegenüber den kürzlich populären Diffusionsmodellen drei Vorteile hat:
(1) Bei derselben Netzwerkstruktur ist die vom ODE von PFGM erzeugte Probenqualität viel besser als die ODE des Diffusionsmodells; 2) Während die Erzeugungsqualität der SDE (stochastische Differentialgleichung) des Diffusionsmodells nahezu gleich ist, hat die ODE von PFGM die 10-fache bis 20-fache Beschleunigung erreicht(3) Die Ausdrucksfähigkeit von PFGM ist strukturell höher robuster als Diffusionsmodelle.
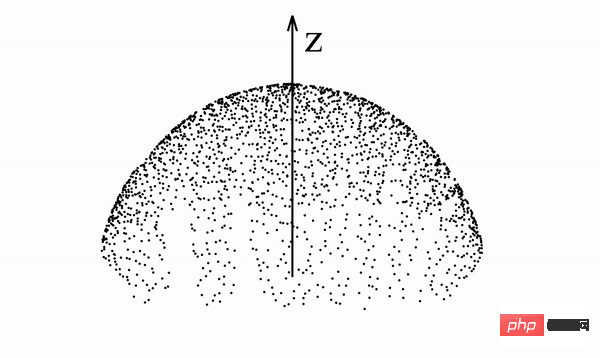
Abbildung 1: Der Probenpunkt bewegt sich entlang der elektrischen Feldlinie. Oben: Die Datenverteilung erfolgt in Form eines Herzens. Unten: Die Daten werden in Form einer PFGM-Vorwärts-ODE und einer Rückwärts-ODE mit PFGM verteilt Beachten Sie, dass der obige Prozess N-dimensionale Daten in den N+1-dimensionalen (zusätzlichen Z-Dimension) Raum einbettet. Um die Unterscheidung zu erleichtern, verwenden Forscher x und wobei Die Trajektorie des elektrischen Feldes Linie (siehe Abbildung 2) kann durch die folgende ODE-Beschreibung berechnet werden: Im folgenden Satz beweisen die Forscher, dass die obige ODE eine Bijektion der gleichmäßigen Verteilung auf der hochdimensionalen Hemisphäre und den Daten definiert Verteilung auf der z=0-Ebene. Diese Schlussfolgerung ist dieselbe wie die Intuition in den Abbildungen 1 und 2: Die Datenverteilung kann durch elektrische Feldlinien wiederhergestellt werden. Training von PFGM Anhand eines aus der Datenverteilung entnommenen Datensatzes Dieser elektrische Feldliniengradient ist das Lernziel. Diese Studie verwendet die perturb-Funktion, um Punkte im Raum auszuwählen, und die Quadratverlustfunktion ermöglicht es dem neuronalen Netzwerk PFGM-Probenahme Nach dem Erlernen der Normalisierung zum Erlernen des normalisierten elektrischen Feldliniengradienten im Raum kann die Datenverteilung über das folgende ODE abgetastet werden: Diese ODE bewirkt, dass sich die Probe allmählich von der großen Kugel entlang der elektrischen Feldlinien zur z=0-Ebene bewegt, indem z reduziert wird. Darüber hinaus schlägt diese Studie vor, die gleichmäßige Verteilung auf einer großen Kugel auf eine bestimmte Z-Ebene zu projizieren, um ODE-Simulationen zu erleichtern und die Probenentnahme durch Variablensubstitution weiter zu beschleunigen. Spezifische Schritte finden Sie in Abschnitt 3.3 des Artikels. In Tabelle 1 verwendet diese Studie den Standarddatensatz CIFAR-10, um verschiedene Modelle zu bewerten. In diesem Datensatz ist PFGM das leistungsstärkste reversible normalisierte Strömungsmodell und erreicht einen FID-Score von 2,35. PFGM bietet eine bessere Leistung als das Diffusionsmodell mit derselben Netzwerkstruktur (DDPM++/DDPM++ tief). Die Forscher stellten außerdem fest, dass die SDE-Generierungsqualität (stochastische Differentialgleichung) des Diffusionsmodells zwar ähnlich war, PFGM jedoch eine 10- bis 20-fache Beschleunigung erreichte, was ein besseres Gleichgewicht zwischen Generierungsqualität und -geschwindigkeit darstellt. Darüber hinaus stellten die Forscher fest, dass PFGM bei Netzwerkstrukturen mit schwächeren Ausdrucksfähigkeiten robuster ist als das Diffusionsmodell und bei höherdimensionalen Datensätzen unter denselben Bedingungen immer noch besser als das Diffusionsmodell. Weitere Informationen finden Sie im experimentellen Abschnitt des Artikels. In Abbildung 3 visualisiert die Studie den Prozess der PFGM-Bilderzeugung. Tabelle 1: Probenqualität (FID, Inception) und Probenschritte (NFE) auf CIFAR-10-Daten Schlussfolgerung Diese Studie schlägt ein generatives PFGM-Modell vor, das auf der Poisson-Gleichung basiert. Dieses Modell sagt normalisierte elektrische Feldliniengradienten in einem erweiterten Raum mit N+1 Dimensionen voraus und wird durch die entsprechenden ODEs der elektrischen Feldlinien abgetastet. In Experimenten ist das in dieser Studie untersuchte Modell derzeit das beste standardisierte Strömungsmodell und erzielte bessere Erzeugungseffekte und eine schnellere Abtastgeschwindigkeit als das Diffusionsmodell auf derselben Netzwerkstruktur. Der Sampling-Prozess von PFGM ist robuster gegenüber Rauschen und kann auch auf höherdimensionale Datensätze erweitert werden. Forscher gehen davon aus, dass PFGM auch in anderen Anwendungsbereichen gute Leistungen erbringen wird, etwa bei der Molekülgenerierung und der 3D-Datengenerierung. Methodenübersicht
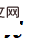 , um N-dimensionale Daten und N+1 Dimensionen darzustellen. Um die oben genannten hochdimensionalen elektrischen Feldlinien zu erhalten, muss die folgende Poisson-Gleichung gelöst werden:
, um N-dimensionale Daten und N+1 Dimensionen darzustellen. Um die oben genannten hochdimensionalen elektrischen Feldlinien zu erhalten, muss die folgende Poisson-Gleichung gelöst werden: 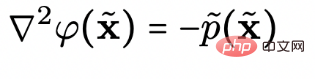
 die Datenverteilung ist, die Sie auf der z=0-Ebene erzeugen möchten;
die Datenverteilung ist, die Sie auf der z=0-Ebene erzeugen möchten;  ist auch die potenzielle Funktion. Dies ist das Ziel, das Forscher lösen wollen. Da nur die Richtung der elektrischen Feldlinie bekannt sein muss, leiteten die Forscher die analytische Form des Gradienten der elektrischen Feldlinie (den Gradienten der Potentialfunktion) ab:
ist auch die potenzielle Funktion. Dies ist das Ziel, das Forscher lösen wollen. Da nur die Richtung der elektrischen Feldlinie bekannt sein muss, leiteten die Forscher die analytische Form des Gradienten der elektrischen Feldlinie (den Gradienten der Potentialfunktion) ab: 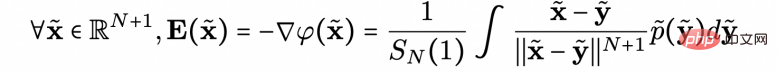


 verwenden die Forscher den dem Datensatz entsprechenden elektrischen Feldliniengradienten, um die entsprechende Datenverteilung anzunähern elektrischer Feldliniengradient:
verwenden die Forscher den dem Datensatz entsprechenden elektrischen Feldliniengradienten, um die entsprechende Datenverteilung anzunähern elektrischer Feldliniengradient: 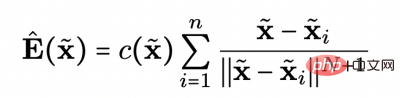
 , den normalisierten elektrischen Feldliniengradienten im Raum zu lernen
, den normalisierten elektrischen Feldliniengradienten im Raum zu lernen  . Der spezifische Algorithmus lautet wie folgt:
. Der spezifische Algorithmus lautet wie folgt: 
Experimentelle Ergebnisse


Das obige ist der detaillierte Inhalt vonrollen! Das Poisson-Strömungserzeugungsmodell des MIT übertrifft das Diffusionsmodell, wenn es um Qualität und Geschwindigkeit geht. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Das weltweit leistungsstärkste Open-Source-MoE-Modell ist da, mit chinesischen Fähigkeiten, die mit GPT-4 vergleichbar sind, und der Preis beträgt nur fast ein Prozent von GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Das weltweit leistungsstärkste Open-Source-MoE-Modell ist da, mit chinesischen Fähigkeiten, die mit GPT-4 vergleichbar sind, und der Preis beträgt nur fast ein Prozent von GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Stellen Sie sich ein Modell der künstlichen Intelligenz vor, das nicht nur die Fähigkeit besitzt, die traditionelle Datenverarbeitung zu übertreffen, sondern auch eine effizientere Leistung zu geringeren Kosten erzielt. Dies ist keine Science-Fiction, DeepSeek-V2[1], das weltweit leistungsstärkste Open-Source-MoE-Modell, ist da. DeepSeek-V2 ist ein leistungsstarkes MoE-Sprachmodell (Mix of Experts) mit den Merkmalen eines wirtschaftlichen Trainings und einer effizienten Inferenz. Es besteht aus 236B Parametern, von denen 21B zur Aktivierung jedes Markers verwendet werden. Im Vergleich zu DeepSeek67B bietet DeepSeek-V2 eine stärkere Leistung, spart gleichzeitig 42,5 % der Trainingskosten, reduziert den KV-Cache um 93,3 % und erhöht den maximalen Generierungsdurchsatz auf das 5,76-fache. DeepSeek ist ein Unternehmen, das sich mit allgemeiner künstlicher Intelligenz beschäftigt
 KI untergräbt die mathematische Forschung! Der Gewinner der Fields-Medaille und der chinesisch-amerikanische Mathematiker führten 11 hochrangige Arbeiten an | Gefällt mir bei Terence Tao
Apr 09, 2024 am 11:52 AM
KI untergräbt die mathematische Forschung! Der Gewinner der Fields-Medaille und der chinesisch-amerikanische Mathematiker führten 11 hochrangige Arbeiten an | Gefällt mir bei Terence Tao
Apr 09, 2024 am 11:52 AM
KI verändert tatsächlich die Mathematik. Vor kurzem hat Tao Zhexuan, der diesem Thema große Aufmerksamkeit gewidmet hat, die neueste Ausgabe des „Bulletin of the American Mathematical Society“ (Bulletin der American Mathematical Society) weitergeleitet. Zum Thema „Werden Maschinen die Mathematik verändern?“ äußerten viele Mathematiker ihre Meinung. Der gesamte Prozess war voller Funken, knallhart und aufregend. Der Autor verfügt über eine starke Besetzung, darunter der Fields-Medaillengewinner Akshay Venkatesh, der chinesische Mathematiker Zheng Lejun, der NYU-Informatiker Ernest Davis und viele andere bekannte Wissenschaftler der Branche. Die Welt der KI hat sich dramatisch verändert. Viele dieser Artikel wurden vor einem Jahr eingereicht.
 Hallo, elektrischer Atlas! Der Boston Dynamics-Roboter erwacht wieder zum Leben, seltsame 180-Grad-Bewegungen machen Musk Angst
Apr 18, 2024 pm 07:58 PM
Hallo, elektrischer Atlas! Der Boston Dynamics-Roboter erwacht wieder zum Leben, seltsame 180-Grad-Bewegungen machen Musk Angst
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas tritt offiziell in die Ära der Elektroroboter ein! Gestern hat sich der hydraulische Atlas einfach „unter Tränen“ von der Bühne der Geschichte zurückgezogen. Heute gab Boston Dynamics bekannt, dass der elektrische Atlas im Einsatz ist. Es scheint, dass Boston Dynamics im Bereich kommerzieller humanoider Roboter entschlossen ist, mit Tesla zu konkurrieren. Nach der Veröffentlichung des neuen Videos wurde es innerhalb von nur zehn Stunden bereits von mehr als einer Million Menschen angesehen. Die alten Leute gehen und neue Rollen entstehen. Das ist eine historische Notwendigkeit. Es besteht kein Zweifel, dass dieses Jahr das explosive Jahr der humanoiden Roboter ist. Netizens kommentierten: Die Weiterentwicklung der Roboter hat dazu geführt, dass die diesjährige Eröffnungsfeier wie Menschen aussieht, und der Freiheitsgrad ist weitaus größer als der von Menschen. Aber ist das wirklich kein Horrorfilm? Zu Beginn des Videos liegt Atlas ruhig auf dem Boden, scheinbar auf dem Rücken. Was folgt, ist atemberaubend
 KAN, das MLP ersetzt, wurde durch Open-Source-Projekte auf Faltung erweitert
Jun 01, 2024 pm 10:03 PM
KAN, das MLP ersetzt, wurde durch Open-Source-Projekte auf Faltung erweitert
Jun 01, 2024 pm 10:03 PM
Anfang dieses Monats schlugen Forscher des MIT und anderer Institutionen eine vielversprechende Alternative zu MLP vor – KAN. KAN übertrifft MLP in Bezug auf Genauigkeit und Interpretierbarkeit. Und es kann MLP, das mit einer größeren Anzahl von Parametern ausgeführt wird, mit einer sehr kleinen Anzahl von Parametern übertreffen. Beispielsweise gaben die Autoren an, dass sie KAN nutzten, um die Ergebnisse von DeepMind mit einem kleineren Netzwerk und einem höheren Automatisierungsgrad zu reproduzieren. Konkret verfügt DeepMinds MLP über etwa 300.000 Parameter, während KAN nur etwa 200 Parameter hat. KAN hat eine starke mathematische Grundlage wie MLP und basiert auf dem universellen Approximationssatz, während KAN auf dem Kolmogorov-Arnold-Darstellungssatz basiert. Wie in der folgenden Abbildung gezeigt, hat KAN
 Google ist begeistert: JAX-Leistung übertrifft Pytorch und TensorFlow! Es könnte die schnellste Wahl für das GPU-Inferenztraining werden
Apr 01, 2024 pm 07:46 PM
Google ist begeistert: JAX-Leistung übertrifft Pytorch und TensorFlow! Es könnte die schnellste Wahl für das GPU-Inferenztraining werden
Apr 01, 2024 pm 07:46 PM
Die von Google geförderte Leistung von JAX hat in jüngsten Benchmark-Tests die von Pytorch und TensorFlow übertroffen und belegt bei 7 Indikatoren den ersten Platz. Und der Test wurde nicht auf der TPU mit der besten JAX-Leistung durchgeführt. Obwohl unter Entwicklern Pytorch immer noch beliebter ist als Tensorflow. Aber in Zukunft werden möglicherweise mehr große Modelle auf Basis der JAX-Plattform trainiert und ausgeführt. Modelle Kürzlich hat das Keras-Team drei Backends (TensorFlow, JAX, PyTorch) mit der nativen PyTorch-Implementierung und Keras2 mit TensorFlow verglichen. Zunächst wählen sie eine Reihe von Mainstream-Inhalten aus
 Tesla-Roboter arbeiten in Fabriken, Musk: Der Freiheitsgrad der Hände wird dieses Jahr 22 erreichen!
May 06, 2024 pm 04:13 PM
Tesla-Roboter arbeiten in Fabriken, Musk: Der Freiheitsgrad der Hände wird dieses Jahr 22 erreichen!
May 06, 2024 pm 04:13 PM
Das neueste Video von Teslas Roboter Optimus ist veröffentlicht und er kann bereits in der Fabrik arbeiten. Bei normaler Geschwindigkeit sortiert es Batterien (Teslas 4680-Batterien) so: Der Beamte hat auch veröffentlicht, wie es bei 20-facher Geschwindigkeit aussieht – auf einer kleinen „Workstation“, pflücken und pflücken und pflücken: Dieses Mal wird es freigegeben. Eines der Highlights Der Vorteil des Videos besteht darin, dass Optimus diese Arbeit in der Fabrik völlig autonom und ohne menschliches Eingreifen während des gesamten Prozesses erledigt. Und aus Sicht von Optimus kann es auch die krumme Batterie aufnehmen und platzieren, wobei der Schwerpunkt auf der automatischen Fehlerkorrektur liegt: In Bezug auf die Hand von Optimus gab der NVIDIA-Wissenschaftler Jim Fan eine hohe Bewertung ab: Die Hand von Optimus ist der fünffingrige Roboter der Welt am geschicktesten. Seine Hände sind nicht nur taktil
 FisheyeDetNet: der erste Zielerkennungsalgorithmus basierend auf einer Fischaugenkamera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: der erste Zielerkennungsalgorithmus basierend auf einer Fischaugenkamera
Apr 26, 2024 am 11:37 AM
Die Zielerkennung ist ein relativ ausgereiftes Problem in autonomen Fahrsystemen, wobei die Fußgängererkennung einer der ersten Algorithmen ist, die eingesetzt werden. In den meisten Arbeiten wurde eine sehr umfassende Recherche durchgeführt. Die Entfernungswahrnehmung mithilfe von Fischaugenkameras für die Rundumsicht ist jedoch relativ wenig untersucht. Aufgrund der großen radialen Verzerrung ist es schwierig, die standardmäßige Bounding-Box-Darstellung in Fischaugenkameras zu implementieren. Um die obige Beschreibung zu vereinfachen, untersuchen wir erweiterte Begrenzungsrahmen-, Ellipsen- und allgemeine Polygondesigns in Polar-/Winkeldarstellungen und definieren eine mIOU-Metrik für die Instanzsegmentierung, um diese Darstellungen zu analysieren. Das vorgeschlagene Modell „fisheyeDetNet“ mit polygonaler Form übertrifft andere Modelle und erreicht gleichzeitig 49,5 % mAP auf dem Valeo-Fisheye-Kameradatensatz für autonomes Fahren
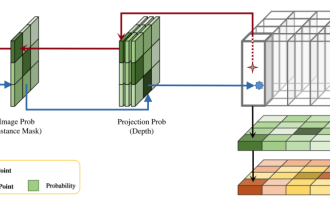 DualBEV: BEVFormer und BEVDet4D deutlich übertreffen, öffnen Sie das Buch!
Mar 21, 2024 pm 05:21 PM
DualBEV: BEVFormer und BEVDet4D deutlich übertreffen, öffnen Sie das Buch!
Mar 21, 2024 pm 05:21 PM
In diesem Artikel wird das Problem der genauen Erkennung von Objekten aus verschiedenen Blickwinkeln (z. B. Perspektive und Vogelperspektive) beim autonomen Fahren untersucht, insbesondere wie die Transformation von Merkmalen aus der Perspektive (PV) in den Raum aus der Vogelperspektive (BEV) effektiv ist implementiert über das Modul Visual Transformation (VT). Bestehende Methoden lassen sich grob in zwei Strategien unterteilen: 2D-zu-3D- und 3D-zu-2D-Konvertierung. 2D-zu-3D-Methoden verbessern dichte 2D-Merkmale durch die Vorhersage von Tiefenwahrscheinlichkeiten, aber die inhärente Unsicherheit von Tiefenvorhersagen, insbesondere in entfernten Regionen, kann zu Ungenauigkeiten führen. Während 3D-zu-2D-Methoden normalerweise 3D-Abfragen verwenden, um 2D-Features abzutasten und die Aufmerksamkeitsgewichte der Korrespondenz zwischen 3D- und 2D-Features über einen Transformer zu lernen, erhöht sich die Rechen- und Bereitstellungszeit.



