 Backend-Entwicklung
Backend-Entwicklung
 Python-Tutorial
Python-Tutorial
 Verwenden Sie Python, um ein Gadget zur Vorhersage von Immobilienpreisen zu erstellen!
Verwenden Sie Python, um ein Gadget zur Vorhersage von Immobilienpreisen zu erstellen!
Verwenden Sie Python, um ein Gadget zur Vorhersage von Immobilienpreisen zu erstellen!

Hallo zusammen.
Dies ist ein Fall der Immobilienpreisvorhersage, der von der Kaggle-Website stammt. Es ist die erste Wettbewerbsfrage für viele Algorithmus-Anfänger.
Dieser Fall umfasst einen vollständigen Prozess zur Lösung von Problemen des maschinellen Lernens, einschließlich EDA, Feature Engineering, Modelltraining, Modellfusion usw.
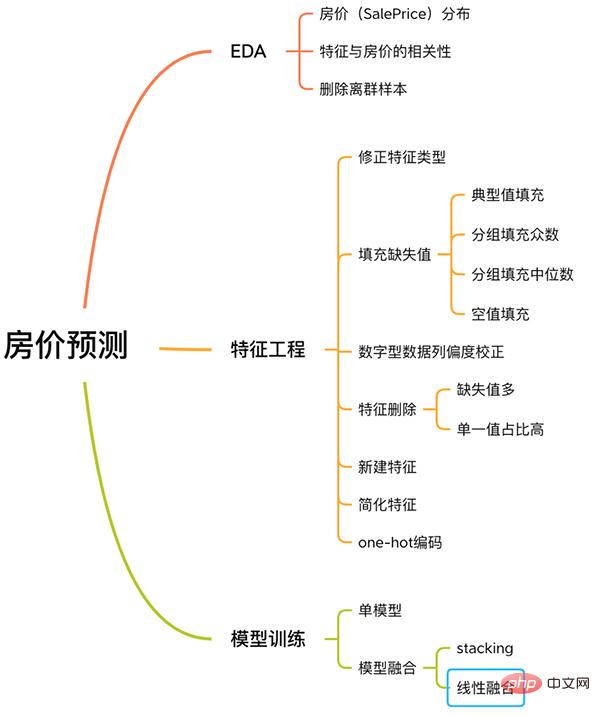
Prozess zur Vorhersage des Hauspreises
Folgen Sie mir unten, um mehr über diesen Fall zu erfahren.
Keine langen Wörter, kein überflüssiger Code, nur einfache Erklärungen.
1. EDA
Der Zweck der explorativen Datenanalyse (EDA) besteht darin, uns ein umfassendes Verständnis des Datensatzes zu vermitteln. In diesem Schritt untersuchen wir folgende Inhalte:

EDA-Inhalt
1.1 Eingabedatensatz
train = pd.read_csv('./data/train.csv')
test = pd.read_csv('./data/test.csv')

Trainingsbeispiele
Train und Test sind der Trainingssatz bzw. der Testsatz mit 1460 Proben bzw. 80 Funktionen.
Die Spalte „SalePrice“ stellt den Immobilienpreis dar, den wir vorhersagen möchten.
1.2 Hauspreisverteilung
Da unsere Aufgabe darin besteht, Hauspreise vorherzusagen, liegt der Schwerpunkt im Datensatz auf der Wertverteilung der Hauspreisspalte (SalePrice).
sns.distplot(train['SalePrice']);
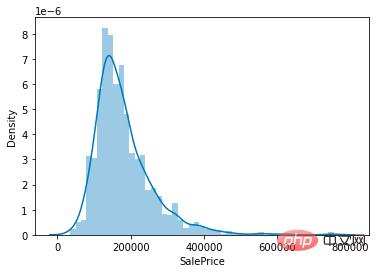
Hauspreiswertverteilung
Wie aus der Abbildung ersichtlich ist, ist der Spitzenwert der SalePrice-Spalte relativ steil und der Spitzenwert ist nach links geneigt.
Sie können die Funktionen skew() und kurt() auch direkt aufrufen, um die spezifischen Schiefe- und Kurtosis-Werte von SalePrice zu berechnen.
Für Situationen, in denen die Schiefe und Kurtosis relativ groß sind, wird empfohlen, log() zu verwenden, um die SalePrice-Spalte zu glätten.
1.3 Merkmale im Zusammenhang mit Immobilienpreisen
Nachdem wir die Verteilung von SalePrice verstanden haben, können wir die Korrelation zwischen 80 Merkmalen und SalePrice berechnen.
Konzentrieren Sie sich auf die 10 Funktionen mit der stärksten Korrelation mit SalePrice.
# 计算列之间相关性
corrmat = train.corr()
# 取 top10
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
# 绘图
cm = np.corrcoef(train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
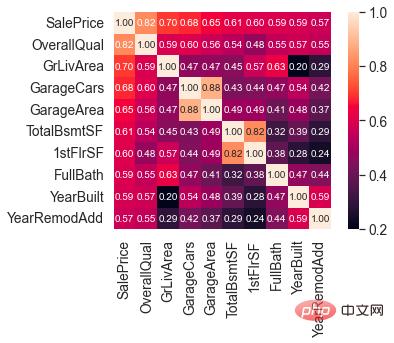
Merkmale, die stark mit SalePrice korrelieren
OverallQual (Hausmaterialien und -oberflächen), GrLivArea (oberirdischer Wohnbereich), GarageCars (Garagenkapazität) und TotalBsmtSF (Kellerfläche) korrelieren stark mit SalePrice.
Diese Funktionen werden später auch bei der Feature-Entwicklung im Mittelpunkt stehen.
1.4 Ausreißerstichproben eliminieren
Da die Stichprobengröße des Datensatzes sehr klein ist, sind Ausreißer für unser späteres Training des Modells nicht förderlich.
Daher ist es notwendig, die Ausreißer jedes numerischen Merkmals zu berechnen und die Stichproben mit den meisten Ausreißern zu eliminieren.
# 获取数值型特征 numeric_features = train.dtypes[train.dtypes != 'object'].index # 计算每个特征的离群样本 for feature in numeric_features: outs = detect_outliers(train[feature], train['SalePrice'],top=5, plot=False) all_outliers.extend(outs) # 输出离群次数最多的样本 print(Counter(all_outliers).most_common()) # 剔除离群样本 train = train.drop(train.index[outliers])
detect_outliers() ist eine benutzerdefinierte Funktion, die den LocalOutlierFactor-Algorithmus der sklearn-Bibliothek verwendet, um Ausreißer zu berechnen.
Zu diesem Zeitpunkt ist EDA abgeschlossen. Abschließend werden der Trainingssatz und der Testsatz zusammengeführt, um das folgende Feature-Engineering durchzuführen.
y = train.SalePrice.reset_index(drop=True) train_features = train.drop(['SalePrice'], axis=1) test_features = test features = pd.concat([train_features, test_features]).reset_index(drop=True)
features kombiniert die Funktionen des Trainingssatzes und des Testsatzes und sind die Daten, die wir im Folgenden verarbeiten werden.
2. Feature Engineering müssen in Textfunktionen umgewandelt werden.features['MSSubClass'] = features['MSSubClass'].apply(str)
features['YrSold'] = features['YrSold'].astype(str)
features['MoSold'] = features['MoSold'].astype(str)
Nach dem Login kopieren
2.2 Füllen fehlender Werte in Features features['MSSubClass'] = features['MSSubClass'].apply(str) features['YrSold'] = features['YrSold'].astype(str) features['MoSold'] = features['MoSold'].astype(str)
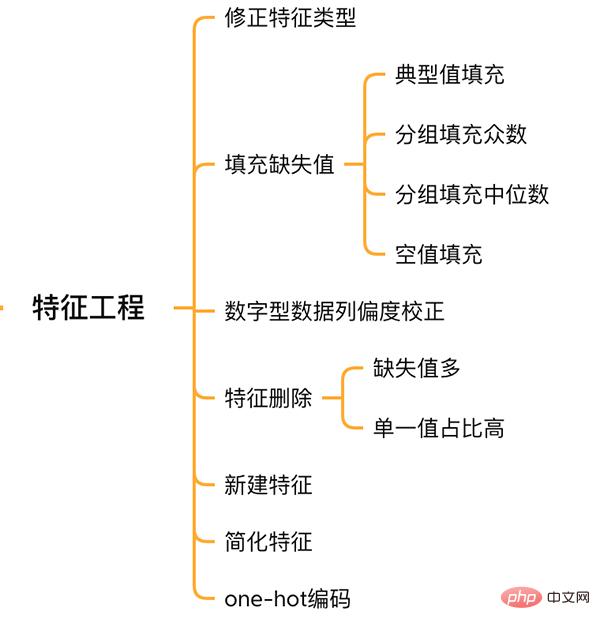 Es gibt keinen einheitlichen Standard zum Füllen fehlender Werte. Es muss anhand verschiedener Features entschieden werden, wie gefüllt werden soll.
Es gibt keinen einheitlichen Standard zum Füllen fehlender Werte. Es muss anhand verschiedener Features entschieden werden, wie gefüllt werden soll.
# Functional:文档提供了典型值 Typ
features['Functional'] = features['Functional'].fillna('Typ') #Typ 是典型值
# 分组填充需要按照相似的特征分组,取众数或中位数
# MSZoning(房屋区域)按照 MSSubClass(房屋)类型分组填充众数
features['MSZoning'] = features.groupby('MSSubClass')['MSZoning'].transform(lambda x: x.fillna(x.mode()[0]))
#LotFrontage(到接到举例)按Neighborhood分组填充中位数
features['LotFrontage'] = features.groupby('Neighborhood')['LotFrontage'].transform(lambda x: x.fillna(x.median()))
# 车库相关的数值型特征,空代表无,使用0填充空值。
for col in ('GarageYrBlt', 'GarageArea', 'GarageCars'):
features[col] = features[col].fillna(0)
2.3 Schiefekorrektur
ähnelt der Erkundung der SalePrice-Spalte und glättet Features mit hoher Schiefe.
# skew()方法,计算特征的偏度(skewness)。 skew_features = features[numeric_features].apply(lambda x: skew(x)).sort_values(ascending=False) # 取偏度大于 0.15 的特征 high_skew = skew_features[skew_features > 0.15] skew_index = high_skew.index # 处理高偏度特征,将其转化为正态分布,也可以使用简单的log变换 for i in skew_index: features[i] = boxcox1p(features[i], boxcox_normmax(features[i] + 1))
2.4 Löschen und Hinzufügen von Features
Features, bei denen fast alle Werte fehlen oder einen hohen Anteil an Einzelwerten (99,94 %) aufweisen, können direkt gelöscht werden.
features = features.drop(['Utilities', 'Street', 'PoolQC',], axis=1)
Gleichzeitig können mehrere Funktionen zusammengeführt werden, um neue Funktionen zu generieren.
Manchmal ist es für das Modell schwierig, die Beziehung zwischen Features zu lernen. Die manuelle Fusion von Features kann die Lernschwierigkeit des Modells verringern und den Effekt verbessern.
# 将原施工日期和改造日期融合 features['YrBltAndRemod']=features['YearBuilt']+features['YearRemodAdd'] # 将地下室面积、1楼、2楼面积融合 features['TotalSF']=features['TotalBsmtSF'] + features['1stFlrSF'] + features['2ndFlrSF']
Es zeigt sich, dass die Funktionen, die wir zusammengeführt haben, alle Funktionen sind, die stark mit SalePrice zusammenhängen.
Vereinfachen Sie abschließend die Features und führen Sie die 01-Verarbeitung für Features mit monotoner Verteilung durch (Beispiel: 99 von 100 Daten haben einen Wert von 0,9 und der andere hat einen Wert von 0,1).
features['haspool'] = features['PoolArea'].apply(lambda x: 1 if x > 0 else 0) features['has2ndfloor'] = features['2ndFlrSF'].apply(lambda x: 1 if x > 0 else 0)
2.6 生成最终训练数据
到这里特征工程就做完了, 我们需要从features中将训练集和测试集重新分离出来,构造最终的训练数据。
X = features.iloc[:len(y), :] X_sub = features.iloc[len(y):, :] X = np.array(X.copy()) y = np.array(y) X_sub = np.array(X_sub.copy())
三. 模型训练
因为SalePrice是数值型且是连续的,所以需要训练一个回归模型。
3.1 单一模型
首先以岭回归(Ridge) 为例,构造一个k折交叉验证模型。
from sklearn.linear_model import RidgeCV from sklearn.pipeline import make_pipeline from sklearn.model_selection import KFold kfolds = KFold(n_splits=10, shuffle=True, random_state=42) alphas_alt = [14.5, 14.6, 14.7, 14.8, 14.9, 15, 15.1, 15.2, 15.3, 15.4, 15.5] ridge = make_pipeline(RobustScaler(), RidgeCV(alphas=alphas_alt, cv=kfolds))
岭回归模型有一个超参数alpha,而RidgeCV的参数名是alphas,代表输入一个超参数alpha数组。在拟合模型时,会从alpha数组中选择表现较好某个取值。
由于现在只有一个模型,无法确定岭回归是不是最佳模型。所以我们可以找一些出场率高的模型多试试。
# lasso lasso = make_pipeline( RobustScaler(), LassoCV(max_iter=1e7, alphas=alphas2, random_state=42, cv=kfolds)) #elastic net elasticnet = make_pipeline( RobustScaler(), ElasticNetCV(max_iter=1e7, alphas=e_alphas, cv=kfolds, l1_ratio=e_l1ratio)) #svm svr = make_pipeline(RobustScaler(), SVR( C=20, epsilon=0.008, gamma=0.0003, )) #GradientBoosting(展开到一阶导数) gbr = GradientBoostingRegressor(...) #lightgbm lightgbm = LGBMRegressor(...) #xgboost(展开到二阶导数) xgboost = XGBRegressor(...)
有了多个模型,我们可以再定义一个得分函数,对模型评分。
#模型评分函数 def cv_rmse(model, X=X): rmse = np.sqrt(-cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv=kfolds)) return (rmse)
以岭回归为例,计算模型得分。
score = cv_rmse(ridge)
print("Ridge score: {:.4f} ({:.4f})n".format(score.mean(), score.std()), datetime.now(), ) #0.1024
运行其他模型发现得分都差不多。
这时候我们可以任选一个模型,拟合,预测,提交训练结果。还是以岭回归为例
# 训练模型
ridge.fit(X, y)
# 模型预测
submission.iloc[:,1] = np.floor(np.expm1(ridge.predict(X_sub)))
# 输出测试结果
submission = pd.read_csv("./data/sample_submission.csv")
submission.to_csv("submission_single.csv", index=False)
submission_single.csv是岭回归预测的房价,我们可以把这个结果上传到 Kaggle 网站查看结果的得分和排名。
3.2 模型融合-stacking
有时候为了发挥多个模型的作用,我们会将多个模型融合,这种方式又被称为集成学习。
stacking 是一种常见的集成学习方法。简单来说,它会定义个元模型,其他模型的输出作为元模型的输入特征,元模型的输出将作为最终的预测结果。
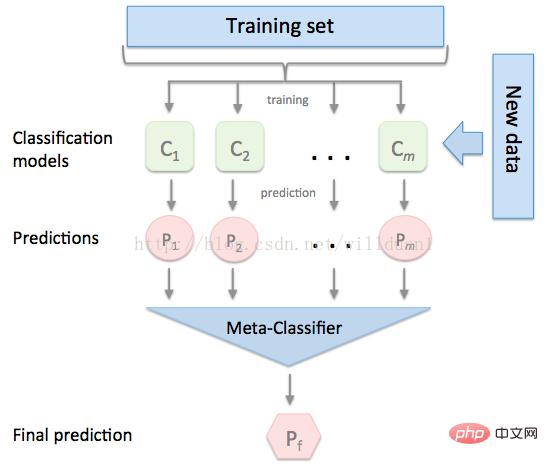
stacking
这里,我们用mlextend库中的StackingCVRegressor模块,对模型做stacking。
stack_gen = StackingCVRegressor( regressors=(ridge, lasso, elasticnet, gbr, xgboost, lightgbm), meta_regressor=xgboost, use_features_in_secondary=True)
训练、预测的过程与上面一样,这里不再赘述。
3.3 模型融合-线性融合
多模型线性融合的思想很简单,给每个模型分配一个权重(权重加和=1),最终的预测结果取各模型的加权平均值。
# 训练单个模型 ridge_model_full_data = ridge.fit(X, y) lasso_model_full_data = lasso.fit(X, y) elastic_model_full_data = elasticnet.fit(X, y) gbr_model_full_data = gbr.fit(X, y) xgb_model_full_data = xgboost.fit(X, y) lgb_model_full_data = lightgbm.fit(X, y) svr_model_full_data = svr.fit(X, y) models = [ ridge_model_full_data, lasso_model_full_data, elastic_model_full_data, gbr_model_full_data, xgb_model_full_data, lgb_model_full_data, svr_model_full_data, stack_gen_model ] # 分配模型权重 public_coefs = [0.1, 0.1, 0.1, 0.1, 0.15, 0.1, 0.1, 0.25] # 线性融合,取加权平均 def linear_blend_models_predict(data_x,models,coefs, bias): tmp=[model.predict(data_x) for model in models] tmp = [c*d for c,d in zip(coefs,tmp)] pres=np.array(tmp).swapaxes(0,1) pres=np.sum(pres,axis=1) return pres
到这里,房价预测的案例我们就讲解完了,大家可以自己运行一下,看看不同方式训练出来的模型效果。
回顾整个案例会发现,我们在数据预处理和特征工程上花费了很大心思,虽然机器学习问题模型原理比较难学,但实际过程中往往特征工程花费的心思最多。
Das obige ist der detaillierte Inhalt vonVerwenden Sie Python, um ein Gadget zur Vorhersage von Immobilienpreisen zu erstellen!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Was sind die für Anfänger geeigneten Digital Currency Trading Apps? Erfahren Sie mehr über den Münzkreis in einem Artikel
Apr 22, 2025 am 08:45 AM
Was sind die für Anfänger geeigneten Digital Currency Trading Apps? Erfahren Sie mehr über den Münzkreis in einem Artikel
Apr 22, 2025 am 08:45 AM
Bei der Auswahl einer für Anfänger geeigneten Handelsplattform für digitale Währung müssen Sie Sicherheit, Benutzerfreundlichkeit, Bildungsressourcen und Kostentransparenz berücksichtigen: 1. Priorität wird Plattformen erteilt, die Kühlspeicher, Zwei-Faktor-Überprüfung und Versicherungsversicherung bieten. 2. Apps mit einfacher Schnittstelle und klarer Betrieb sind für Anfänger besser geeignet. 3. Die Plattform sollte Lernwerkzeuge wie Tutorials und Marktanalysen bereitstellen. 4. Achten Sie auf versteckte Kosten wie Transaktionsgebühren und Barauszahlungsgebühren.
 Die zehn Top-Empfehlungen zur Plattform für Echtzeitdaten auf den Währungskreismärkten werden veröffentlicht
Apr 22, 2025 am 08:12 AM
Die zehn Top-Empfehlungen zur Plattform für Echtzeitdaten auf den Währungskreismärkten werden veröffentlicht
Apr 22, 2025 am 08:12 AM
Zu den für Anfängern geeigneten Kryptowährungsdatenplattformen gehören CoinMarketCap und nicht-kleine Trompete. 1. CoinmarketCap bietet globale Rangliste für den Preis, den Marktwert und der Handelsvolumen für Anfänger für Anfänger und Grundanalyse. 2. Das nichtklammernde Angebot bietet eine chinesisch-freundliche Schnittstelle, die chinesischen Benutzern geeignet ist, um potenzielle Projekte mit geringem Risiko schnell zu untersuchen.
 Was sind die Software -Websites für freie Marktansicht? Ranking der Top Ten Free Market Viewing Software im Währungskreis
Apr 22, 2025 am 10:57 AM
Was sind die Software -Websites für freie Marktansicht? Ranking der Top Ten Free Market Viewing Software im Währungskreis
Apr 22, 2025 am 10:57 AM
Die drei besten zehn Top -Marktansichtssoftware im Währungskreis sind OKX, Binance und Gate.io. 1. OKX bietet eine einfache Schnittstelle und Echtzeitdaten, die eine Vielzahl von Diagrammen und Marktanalysen unterstützt. 2. Binance hat leistungsstarke Funktionen, genaue Daten und eignet sich für alle Arten von Händlern. 3.. Gate.io ist bekannt für seine Stabilität und Vollständigkeit und für langfristige und kurzfristige Anleger geeignet.
 Zuverlässige und benutzerfreundliche Empfehlungen für virtuelle Währungsaustausch-App-App Die neueste Rangliste der zehn besten Börsen im Währungskreis
Apr 22, 2025 pm 01:21 PM
Zuverlässige und benutzerfreundliche Empfehlungen für virtuelle Währungsaustausch-App-App Die neueste Rangliste der zehn besten Börsen im Währungskreis
Apr 22, 2025 pm 01:21 PM
Die zuverlässigen und benutzerfreundlichen Virtual Currency Exchange-Apps sind: 1. Binance, 2. OKX, 3. Gate.io, 4. Coinbase, 5. Kraken, 6. Huobi Global, 7. Bitfinex, 8. Kucoin, 9. Bittrex, 10. Poloniex. Diese Plattformen wurden als das Beste für ihre Transaktionsvolumen, die Benutzererfahrung und -sicherheit ausgewählt, und alle bieten Registrierung, Überprüfung, Einzahlung, Auszahlung und Transaktionsvorgänge an.
 Was sind die Handelsplattformen für digitale Währung im Jahr 2025? Die neuesten Ranglisten der zehn besten Apps für digitale Währung
Apr 22, 2025 pm 03:09 PM
Was sind die Handelsplattformen für digitale Währung im Jahr 2025? Die neuesten Ranglisten der zehn besten Apps für digitale Währung
Apr 22, 2025 pm 03:09 PM
Empfohlene Apps für die zehn besten Plattformen für virtuelle Währung: 1. OKX, 2. Binance, 3. Gate.io, 4. Huobi, 5. Coinbase, 6. Kraken, 7. Bitfinex, 8. Kucoin, 9. Bybit, 10. Bitstamp, diese Plattformen liefern Echtzeit-Markttrends, technische Analyse-Tools und Benutzern und Benutzern, und es mithilfe von Hilfsmittel und Hilfsmittel und Hilfsmittel, die Hilfsmittel für Hilfsmittel und Hilfsmittel für Hilfsmittel und Hilfsmittel für Hilfsmittel und Hilfsmittel zuhilfe liefern.
 Meme Coin Exchange Ranking Meme Coin Haupttausch Top 10 Spots
Apr 22, 2025 am 09:57 AM
Meme Coin Exchange Ranking Meme Coin Haupttausch Top 10 Spots
Apr 22, 2025 am 09:57 AM
Zu den am besten geeigneten Plattformen für Handelsmeme -Münzen gehören: 1. Binance, die weltweit größte, mit hoher Liquidität und niedrigem Handhabungsgebühren; 2. OKX, eine effiziente Handelsmotor, die eine Vielzahl von Meme -Münzen unterstützt; 3. Xbit, dezentralisiert und unterstützt den Handel mit dem Cross-Chain; 4. REDIM (Solana Dex), niedrige Kosten, kombiniert mit Serumbestellbuch; 5. Pancakeswap (BSC Dex), niedrige Transaktionsgebühren und schnelle Geschwindigkeit; 6. Orca (Solana Dex), Benutzererfahrungsoptimierung; 7. Coinbase, hohe Sicherheit, geeignet für Anfänger; 8. Huobi, bekannt in Asien, reiche Handelspaare; 9. Dexrabbit, intelligent
 Tipps und Empfehlungen für die zehn wichtigsten Marktwebsites im Währungskreis 2025
Apr 22, 2025 am 08:03 AM
Tipps und Empfehlungen für die zehn wichtigsten Marktwebsites im Währungskreis 2025
Apr 22, 2025 am 08:03 AM
In den inländischen Benutzeranpassungslösungen werden Konformitätskanäle und Lokalisierungstools gehören. 1. Compliance -Kanäle: Franchise -Währungsaustausch über OTC -Plattformen wie Circle Trade, im Inland müssen sie durch Hongkong- oder Überseeplattformen gehen. 2. Lokalisierungsinstrumente: Verwenden Sie das Währungskreisnetz, um chinesische Informationen zu erhalten, und die Huobi Global Station bietet ein Handelsanschluss von Meta-Universitäten.
 Eine Liste spezieller Dienste für wichtige Handelsplattformen für virtuelle Währung
Apr 22, 2025 am 08:09 AM
Eine Liste spezieller Dienste für wichtige Handelsplattformen für virtuelle Währung
Apr 22, 2025 am 08:09 AM
Institutionelle Anleger sollten konforme Plattformen wie Coinbase Pro und Genesis Trading wählen, die sich auf Kühlspeicherverhältnisse und die Überwachung der Transparenz konzentrieren. Einzelhandelsinvestoren sollten große Plattformen wie Binance und Huobi auswählen und sich auf Benutzererfahrung und Sicherheit konzentrieren. Benutzer in konform-sensitiven Gebieten können durch Circle Trade und Huobi Global Fiat-Währungshandel durchführen, und chinesische Benutzer auf dem Festland müssen konforme rezeptfreie Kanäle durchlaufen.





