CRPS: Bewertungsfunktion für Bayesianische Modelle des maschinellen Lernens

Continuous Ranked Probability Score (CRPS) oder „Continuous Ranked Probability Score“ ist eine Funktion oder Statistik, die Verteilungsvorhersagen mit wahren Werten vergleicht.

Ein wichtiger Teil des maschinellen Lernworkflows ist die Modellbewertung. Der Prozess selbst kann als gesunder Menschenverstand angesehen werden: Teilen Sie die Daten in Trainings- und Testsätze auf, trainieren Sie das Modell auf dem Trainingssatz und verwenden Sie eine Bewertungsfunktion, um seine Leistung auf dem Testsatz zu bewerten.

Eine Bewertungsfunktion (oder Metrik) ordnet wahre Werte und ihre Vorhersagen einem einzigen und vergleichbaren Wert zu [1]. Für kontinuierliche Prognosen können Sie beispielsweise Scoring-Funktionen wie RMSE, MAE, MAPE oder R-Quadrat verwenden. Was ist, wenn es sich bei der Prognose nicht um eine punktuelle Schätzung, sondern um eine Verteilung handelt?

Beim Bayes'schen maschinellen Lernen sind Vorhersagen normalerweise keine punktuellen Schätzungen, sondern eher Verteilungen von Werten. Die Vorhersagen können beispielsweise geschätzte Parameter einer Verteilung oder im nichtparametrischen Fall eine Reihe von Stichproben aus einer MCMC-Methode sein.

In diesem Fall eignen sich herkömmliche Bewertungsfunktionen nicht für das statistische Design; die Aggregation vorhergesagter Verteilungen in ihren Mittelwert oder Median führt zum Verlust erheblicher Informationen über die Streuung und Form der vorhergesagten Verteilung.

CRPS

Continuous Graded Probability Score (CRPS) ist eine Bruchfunktion, die einen einzelnen wahren Wert mit einer kumulativen Verteilungsfunktion (CDF) vergleicht:

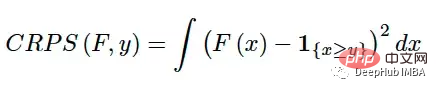
Sie wurde erstmals in den 1970er Jahren eingeführt [4] und wird hauptsächlich verwendet Die Wettervorhersage erhält nun in der Literatur und in der Industrie erneut Aufmerksamkeit [1][6]. Es kann als Metrik zur Bewertung der Modellleistung verwendet werden, wenn die Zielvariable kontinuierlich ist und das Modell die Verteilung des Ziels vorhersagt. Beispiele hierfür sind Bayes'sche Regression oder Bayes'sche Zeitreihenmodelle [5].

CRPS ist sowohl für parametrische als auch für nichtparametrische Vorhersagen mithilfe von CDF nützlich: Für viele Verteilungen verfügt CRPS [3] über einen analytischen Ausdruck, und für nichtparametrische Vorhersagen verwendet CRPS die empirische kumulative Verteilungsfunktion (eCDF).

Nach der Berechnung des CRPS für jede Beobachtung im Testsatz müssen Sie die Ergebnisse auch zu einem einzigen Wert zusammenfassen. Ähnlich wie bei RMSE und MAE werden sie mithilfe eines (möglicherweise gewichteten) Mittelwerts zusammengefasst:

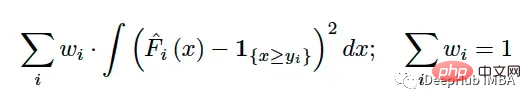
Die größte Herausforderung beim Vergleich eines einzelnen Werts mit einer Verteilung besteht darin, den einzelnen Wert in eine Darstellung der Verteilung umzuwandeln. CRPS löst dieses Problem, indem es die Grundwahrheit in eine entartete Verteilung mit einer Indikatorfunktion umwandelt. Wenn der wahre Wert beispielsweise 7 ist, können wir Folgendes verwenden:

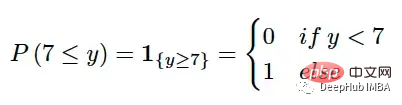
Die Indikatorfunktion ist ein gültiger CDF und kann alle Anforderungen eines CDF erfüllen. Die vorhergesagte Verteilung kann dann mit der degenerierten Verteilung der wahren Werte verglichen werden. Wir möchten auf jeden Fall, dass die vorhergesagte Verteilung der Realität so nahe wie möglich kommt. Daher kann dies mathematisch ausgedrückt werden, indem die (quadratische) Fläche zwischen diesen beiden CDFs gemessen wird:

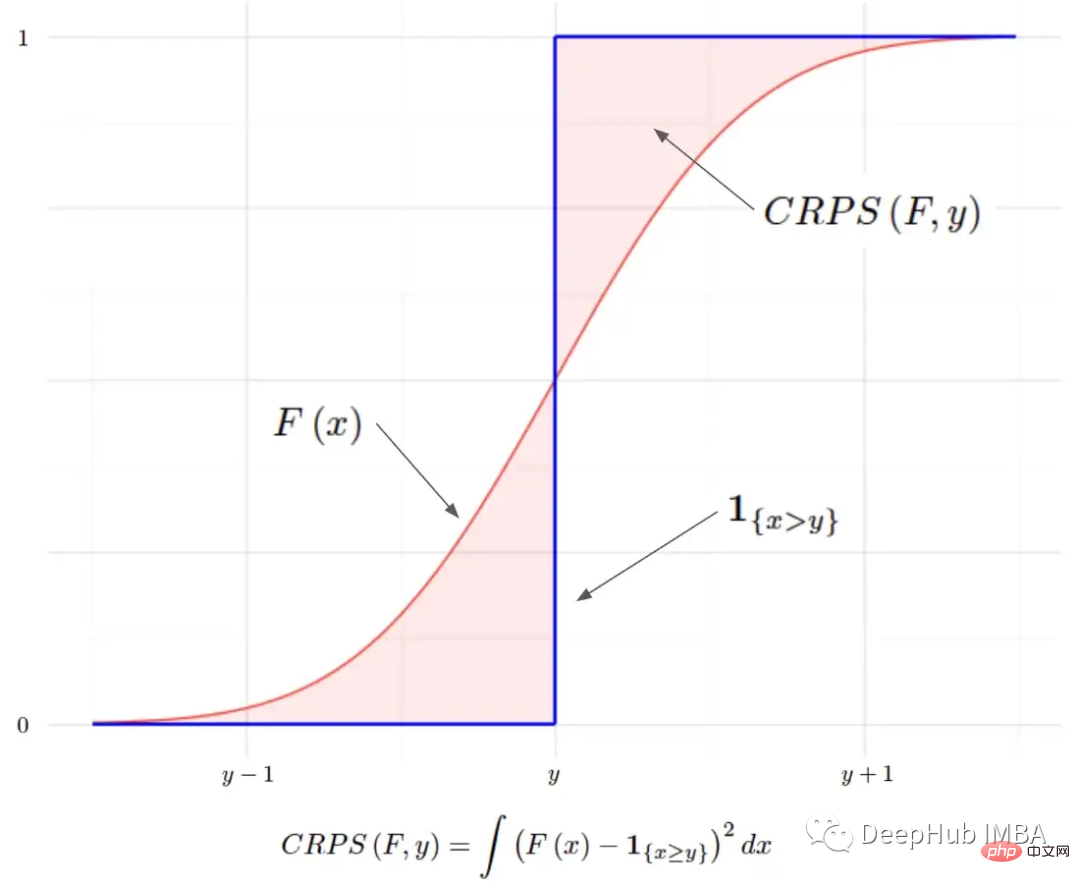
MAE-zu-MAE-Beziehung

CRPS zum berühmten MAE ( Mittlerer absoluter Fehler) hängen eng zusammen. Wenn wir eine punktweise Vorhersage nehmen, sie als degenerierte CDF behandeln und in die CRPS-Gleichung einfügen, erhalten wir:

Wenn die Vorhersageverteilung also eine degenerierte Verteilung ist (z. B. punktweise Schätzung), wird dies beim CRPS der Fall sein auf MAE reduzieren. Dies hilft uns, CRPS aus einer anderen Perspektive zu verstehen: Es kann als Verallgemeinerung von MAE auf die Vorhersage von Verteilungen angesehen werden oder als MAE als Sonderfall von CRPS, wenn die Vorhersageverteilung degeneriert.

Wenn die Vorhersage des Modells eine parametrische Verteilung ist (z. B. müssen Verteilungsparameter vorhergesagt werden), verfügt CRPS über einen analytischen Ausdruck für einige gängige Verteilungen [3]. Wenn das Modell die Parameter μ und σ der Normalverteilung vorhersagt, kann das CRPS mit der folgenden Formel berechnet werden:

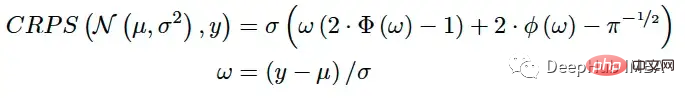
Dieses Schema kann für bekannte Verteilungen wie Beta-, Gamma-, Logistik-, Lognormalverteilung und andere lösen [3 ].

Die Berechnung des eCDF ist eine mühsame Aufgabe, wenn die Vorhersage nichtparametrisch ist, oder genauer gesagt, wenn die Vorhersage eine Reihe von Simulationen ist. Aber CRPS kann auch ausgedrückt werden als:

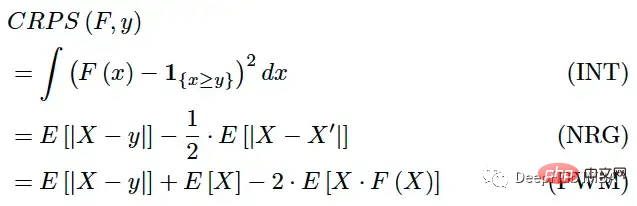
wobei X, X' F-unabhängig und identisch verteilt sind. Diese Ausdrücke sind einfacher zu berechnen, erfordern jedoch noch einige Berechnungen.

Python-Implementierung

import numpy as np
 
 
 # Adapted to numpy from pyro.ops.stats.crps_empirical
 # Copyright (c) 2017-2019 Uber Technologies, Inc.
 # SPDX-License-Identifier: Apache-2.0
 def crps(y_true, y_pred, sample_weight=None):
 num_samples = y_pred.shape[0]
 absolute_error = np.mean(np.abs(y_pred - y_true), axis=0)
 
 if num_samples == 1:
 return np.average(absolute_error, weights=sample_weight)
 
 y_pred = np.sort(y_pred, axis=0)
 diff = y_pred[1:] - y_pred[:-1]
 weight = np.arange(1, num_samples) * np.arange(num_samples - 1, 0, -1)
 weight = np.expand_dims(weight, -1)
 
 per_obs_crps = absolute_error - np.sum(diff * weight, axis=0) / num_samples**2
 return np.average(per_obs_crps, weights=sample_weight)

CRPS-Funktion gemäß NRG-Formular [2] implementiert. Angepasst von pyroppl[6]

import numpy as np
 
 
 def crps(y_true, y_pred, sample_weight=None):
 num_samples = y_pred.shape[0]
 absolute_error = np.mean(np.abs(y_pred - y_true), axis=0)
 
 if num_samples == 1:
 return np.average(absolute_error, weights=sample_weight)
 
 y_pred = np.sort(y_pred, axis=0)
 b0 = y_pred.mean(axis=0)
 b1_values = y_pred * np.arange(num_samples).reshape((num_samples, 1))
 b1 = b1_values.mean(axis=0) / num_samples
 
 per_obs_crps = absolute_error + b0 - 2 * b1
 return np.average(per_obs_crps, weights=sample_weight)

Der obige Code implementiert CRPS basierend auf der PWM-Form[2].

Zusammenfassung

Der Continuous Ranked Probability Score (CRPS) ist eine Bewertungsfunktion, die einen einzelnen wahren Wert mit seiner vorhergesagten Verteilung vergleicht. Diese Eigenschaft macht es für das Bayes'sche maschinelle Lernen relevant, wo Modelle typischerweise Verteilungsvorhersagen statt punktueller Schätzungen ausgeben. Es kann als eine Verallgemeinerung des bekannten MAE zur Verteilungsvorhersage angesehen werden.

Es verfügt über analytische Ausdrücke für parametrische Vorhersagen und kann einfache Berechnungen für nichtparametrische Vorhersagen durchführen. CRPS könnte zur neuen Standardmethode zur Bewertung der Leistung von Bayes'schen Modellen für maschinelles Lernen mit kontinuierlichen Zielen werden.

Das obige ist der detaillierte Inhalt vonCRPS: Bewertungsfunktion für Bayesianische Modelle des maschinellen Lernens. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!