 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Skalierung von sphärischem Deep Learning auf hochauflösende Eingabedaten
Skalierung von sphärischem Deep Learning auf hochauflösende Eingabedaten
Skalierung von sphärischem Deep Learning auf hochauflösende Eingabedaten
Übersetzer |. Zhu Xianzhong
Rezensent |.Traditionelles sphärisches CNN kann nicht auf hochauflösende Klassifizierungsaufgaben erweitert werden. In diesem Artikel stellen wir sphärische Streuschichten vor, eine neue Art von sphärischen Schichten, die die Dimensionalität von Eingabedaten reduzieren und gleichzeitig relevante Informationen beibehalten und Rotationsäquivarianzeigenschaften aufweisen können.
Streunetzwerke funktionieren, indem sie vordefinierte Faltungsfilter aus der Wavelet-Analyse verwenden, anstatt Faltungsfilter von Grund auf zu lernen. Da die Gewichte der Streuschicht spezifisch entworfen und nicht erlernt werden, kann die Streuschicht als einmaliger Vorverarbeitungsschritt verwendet werden, wodurch die Auflösung der Eingabedaten verringert wird. Unsere bisherigen Erfahrungen zeigen, dass sphärische CNNs, die mit einer anfänglichen Streuschicht ausgestattet sind, auf Auflösungen von mehreren zehn Millionen Pixeln skaliert werden können, eine Leistung, die mit herkömmlichen sphärischen CNN-Schichten bisher nicht möglich war.
Traditionelle sphärische Deep-Learning-Methoden erfordern Berechnungen
Spherical CNN (Dokument 1, 2, 3) ist sehr nützlich für die Lösung vieler verschiedener Arten von Problemen beim maschinellen Lernen, da die Datenquellen vieler dieser Probleme nicht auf natürliche Weise dargestellt werden können in einem Flugzeug (eine einführende Einführung hierzu finden Sie in unserem vorherigen Artikel unter: https://towardsdatascience.com/gemetric-deep-learning-for-spherical-data-55612742d05f).
Ein Hauptmerkmal sphärischer CNNs ist, dass sie äquivariant zur Rotation sphärischer Daten sind (in diesem Artikel konzentrieren wir uns auf rotationsäquivariante Methoden). In der Praxis bedeutet dies, dass sphärische CNNs über beeindruckende Generalisierungseigenschaften verfügen, die es ihnen ermöglichen, beispielsweise Netze von 3D-Objekten zu klassifizieren, unabhängig davon, wie sie gedreht werden (und ob sie das Netz beim Training verschiedener Rotationen sehen).
Wir
ineinem aktuellen Artikel beschrieben Kagenova Team eine Reihe von Fortschritten , die entwickelt wurden, um die Recheneffizienz von sphärischem CNN zu verbessern Ergebnisse ( Referenz Adresse: https://towardsdatascience.com/efficient-generalized-spherical-cnns-1493426362ca). Die von uns verwendete Methode - effizientes verallgemeinertes sphärisches CNN - behält nicht nur die gleichen Varianzeigenschaften des traditionellen sphärischen CNN bei, sondern macht gleichzeitig die Berechnung besser effizient ( Dokumentation 1). Trotz dieser Fortschritte in der Recheneffizienz sind sphärische CNNs jedoch immer noch auf Daten mit relativ niedriger Auflösung beschränkt. Das bedeutet, dass , sphärische CNNs derzeit nicht auf spannende Anwendungsszenarien angewendet werden können, bei denen es sich normalerweise um Daten mit höherer Auflösung handelt, wie z. B. kosmologische Datenanalyse und 360 für Virtual Reality. Abschluss in Computer Vision und anderen Bereichen. In einem kürzlich veröffentlichten Artikel haben wir ein sphärisches Streuschichtnetzwerk vorgestellt, um ein effizientes allgemeines sphärisches CNN flexibel anzupassen , um die Auflösung zu verbessern (Dokument 4), in diesem Artikel werden wir darauf eingehen Überprüfen Sie diesen Inhalt. Hybrider Ansatz zur Unterstützung hochauflösender EingabedatenBei der Entwicklung eines effizienten allgemeinen sphärischen CNN (Ref. 1) haben wir einen sehr effektiven Hybridansatz zum Aufbau einer sphärischen CNN-Architektur entdeckt. Hybrid Spherical CNN kann verschiedene Arten sphärischer CNN-Schichten im selben Netzwerk verwenden, sodass Entwickler die Vorteile verschiedener Schichttypen in unterschiedlichen Verarbeitungsstadien nutzen können.
Das obige Bild zeigt ein Beispiel einer hybriden sphärischen CNN-Architektur (bitte beachten Sie: Diese Schichten sind nicht einzeln, sondern einige verschiedene Arten sphärischer CNN-Schichten).
Scattering Networks on Spheres führt diesen hybriden Ansatz fort und führt eine neue sphärische CNN-Schicht ein, die in bestehende sphärische Architekturen eingebunden werden kann. Um das effiziente allgemeine sphärische CNN auf höhere Dimensionen auszudehnen, muss diese neue Schicht die folgenden Eigenschaften aufweisen: 🎜🎜#
- Mischt Informationen zu niedrigen Frequenzen, damit nachfolgende Schichten ausgeführt werden können niedrigere Auflösungen
- Rotationsäquivarianz# 🎜🎜#
- Sorgen Sie für eine stabile und lokal invariante Darstellung (d. h. stellen Sie einen effizienten Darstellungsraum bereit)
- #🎜🎜 #Wir haben festgestellt, dass die Streunetzwerkschicht das Potenzial hat, alle oben aufgeführten Merkmale zu erfüllen.
- Streunetzwerk auf einer Kugel
Die Datenverarbeitung innerhalb der Streuschicht wird durch drei Grundoperationen durchgeführt. Der erste Baustein ist die feste Wavelet-Faltung, die der normalen Lernfaltung ähnelt, die im euklidischen CNN verwendet wird. Nach der Wavelet-Faltung wendet das Streunetzwerk einen modularen nichtlinearen Ansatz auf die resultierende Darstellung an. Schließlich nutzt die Streuung eine Skalierungsfunktion, die einen lokalen Mittelungsalgorithmus mit einigen Ähnlichkeiten zu den Pooling-Schichten in gewöhnlichen CNNs ausführt. Durch wiederholte Anwendung dieser drei Bausteine werden die Eingabedaten in einen Rechenbaum gestreut und die resultierende Darstellung (ähnlich einem CNN-Kanal) in verschiedenen Verarbeitungsstadien aus dem Baum extrahiert. Ein vereinfachtes Schema dieser Vorgänge ist unten dargestellt.
Diese Abbildung veranschaulicht das sphärische Streunetzwerk des sphärischen Signals f. Das Signal wird über eine kaskadierte sphärische Wavelet-Transformation in Kombination mit einer durch rote Knoten dargestellten Absolutwertaktivierungsfunktion verbreitet. Die Ausgabe des Streunetzwerks wird durch Projizieren dieser Signale auf eine sphärische Wavelet-Skalierungsfunktion erhalten, was zu den Streukoeffizienten führt, die durch blaue Knoten dargestellt werden.
Aus einer traditionellen Deep-Learning-Perspektive mag der Betrieb dezentraler Netzwerke etwas unklar erscheinen. Jede beschriebene Rechenoperation hat jedoch einen spezifischen Zweck – nämlich die Nutzung der zuverlässigen theoretischen Ergebnisse der Wavelet-Analyse. 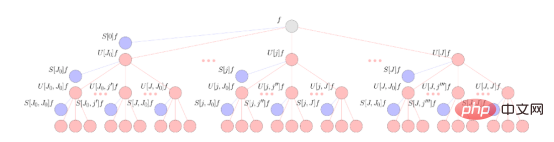
Wavelet-Faltungen in Streunetzwerken werden sorgfältig abgeleitet, um relevante Informationen aus den Eingabedaten zu extrahieren. Beispielsweise werden Wavelets für natürliche Bilder definiert, um speziell Informationen zu Kanten bei hohen Frequenzen und allgemeinen Formen von Objekten bei niedrigen Frequenzen zu extrahieren. Daher können Streunetzwerkfilter in einer planaren Umgebung einige Ähnlichkeiten mit herkömmlichen CNN-Filtern aufweisen. Das Gleiche gilt für die sphärische Einstellung, bei der wir skalendiskretisierte Wavelets verwenden (Einzelheiten siehe Ref. 4).
Da der Wavelet-Filter fest ist, muss die anfängliche Streuschicht nur einmal angewendet werden und muss nicht während des gesamten Trainingsprozesses wiederholt angewendet werden (wie die anfängliche Schicht). im traditionellen CNN). Dadurch wird das Streunetzwerk rechnerisch skalierbar und erfüllt die Anforderungen von Merkmal 1 oben. Darüber hinaus reduziert die Streuschicht die Dimensionalität ihrer Eingabedaten, was bedeutet, dass beim Training nachgeschalteter CNN-Schichten nur begrenzter Speicherplatz zum Zwischenspeichern der Streudarstellung verwendet werden muss.
Die nichtlineare Modulmethode wird hinter der Wavelet-Faltung verwendet. Erstens werden dadurch nichtlineare Eigenschaften in die Schichten des neuronalen Netzwerks eingebracht. Zweitens mischt die Moduloperation die Hochfrequenzinformationen im Eingangssignal in die Niederfrequenzdaten, um die obige Anforderung 2 zu erfüllen. Die folgende Abbildung zeigt die Häufigkeitsverteilung der Wavelet-Darstellung der Daten vor und nach der nichtlinearen Modulberechnung.
Die obige Abbildung zeigt die Verteilung der Wavelet-Koeffizienten bei verschiedenen sphärischen Frequenzen l vor und nach dem modularen Betrieb. Die Energie im Eingangssignal bewegt sich von hohen Frequenzen (linkes Feld) zu niedrigen Frequenzen (rechtes Feld). Dabei ist f das Eingangssignal und Ψ das Wavelet der Skalierung j.
Nach Anwendung der Modulberechnung wird das resultierende Signal auf die Skalierungsfunktion projiziert. Die Skalierungsfunktion extrahiert niederfrequente Informationen aus den Darstellungsergebnissen, ähnlich der Pooling-Funktionsoperation im herkömmlichen CNN. 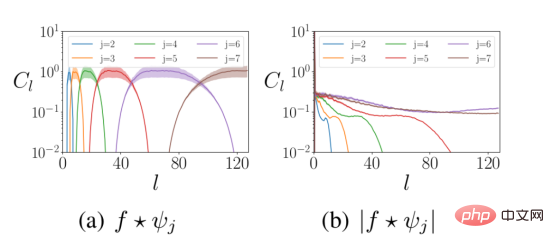
Wir haben die theoretischen Eigenschaften gleicher Varianz sphärischer Streunetzwerke empirisch getestet. Der Test wird durchgeführt, indem das Signal gedreht und durch das Streunetzwerk geleitet wird und dann die resultierende Darstellung mit der resultierenden Darstellung der Eingabedaten nach Durchlaufen des Streunetzwerks verglichen und anschließend die Rotationsberechnung durchgeführt wird. Anhand der Daten in der folgenden Tabelle kann gezeigt werden, dass der gleiche Varianzfehler für eine bestimmte Tiefe gering ist und somit die obige Anforderung 3 erfüllt (normalerweise wird in der Praxis eine Pfadtiefe nicht die Tiefe von zwei Pfaden überschreiten, da die meisten davon Signalenergie wurde bereits erfasst).
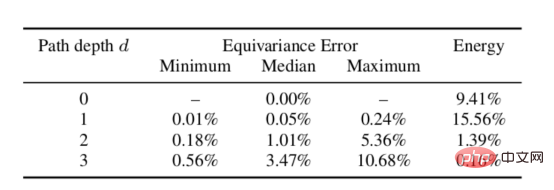
Rotationsgleicher Varianzfehler des sphärischen Streunetzwerks in verschiedenen Tiefen
Schließlich ist theoretisch bewiesen, dass das euklidische Streunetzwerk gegenüber kleinen Differenzen oder Verzerrungen stabil ist (Literatur 5. ). Derzeit dieses Ergebnis wurde auf Streunetzwerke auf kompakten Riemannschen Mannigfaltigkeiten (Dokument 6), insbesondere sphärische Umgebungen (Dokument 4) ausgeweitet. In der Praxis bedeutet Stabilität gegenüber Disparitätsmorphologie, dass sich die vom Streunetzwerk berechnete Darstellung nicht wesentlich unterscheidet, wenn die Eingabe geringfügig geändert wird (siehe unseren vorherigen Beitrag für eine Diskussion der Rolle der Stabilität beim geometrischen Deep Learning , Die Adresse lautet https://towardsdatascience.com/a-brief-introduction-to-geometrische-deep-learning-dae114923ddb). Somit stellen Streunetzwerke einen gut funktionierenden Darstellungsraum bereit, auf dem nachfolgendes Lernen effizient durchgeführt werden kann und die Anforderung 4 oben erfüllt.
Skalierbares und rotationsäquivariantes sphärisches CNN
Unter Berücksichtigung der Tatsache, dass die eingeführten Streuschichten alle unsere gewünschten Eigenschaften erfüllen, sind wir als nächstes bereit, sie in unser hybrides sphärisches CNN zu integrieren. Wie bereits erwähnt, kann die Streuschicht als erster Vorverarbeitungsschritt auf der vorhandenen Architektur fixiert werden, um die Größe der Darstellung für die anschließende Verarbeitung der sphärischen Schicht zu reduzieren.
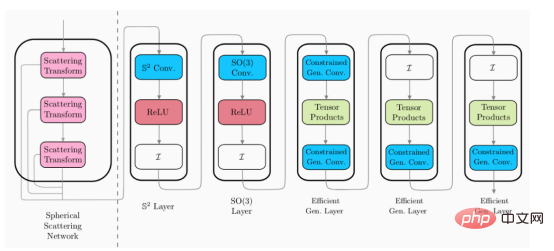
Im Bild oben ist das Streuschichtmodul (links von der gestrichelten Linie) eine Designebene. Dies bedeutet, dass kein Training erforderlich ist, während die verbleibenden Schichten (rechts von der gepunkteten Linie) trainierbar sind. Dies bedeutet daher, dass Streuschichten als einmaliger Vorverarbeitungsschritt angewendet werden können, um die Dimensionalität der Eingabedaten zu reduzieren.
Da Streunetzwerke eine feste Darstellung einer bestimmten Eingabe haben, können Streunetzwerkschichten zu Beginn des Trainings einmal auf den gesamten Datensatz angewendet werden, und die resultierende niedrigdimensionale Darstellung wird zwischengespeichert, um nachfolgende Schichten zu trainieren. Glücklicherweise haben Streudarstellungen eine reduzierte Dimensionalität, was bedeutet, dass der für ihre Speicherung erforderliche Speicherplatz relativ gering ist. Aufgrund der Existenz dieser neuen sphärischen Streuschicht kann das effiziente verallgemeinerte sphärische CNN auf den Bereich hochauflösender Klassifizierungsprobleme erweitert werden.
Klassifizierung der kosmischen Mikrowellen-Hintergrundanisotropie
Wie ist Materie im Universum verteilt? Dies ist eine grundlegende Forschungsfrage für Kosmologen und hat erhebliche Auswirkungen auf theoretische Modelle des Ursprungs und der Entwicklung unseres Universums. Der kosmische Mikrowellenhintergrund (CMB) – Restenergie des Urknalls – bildet die Verteilung der Materie im Universum ab. Kosmologen beobachten die CMB auf der Himmelssphäre, was Rechenmethoden erfordert, die eine kosmologische Analyse innerhalb der Himmelssphäre ermöglichen.
Kosmologen sind sehr an Methoden zur Analyse des kosmischen Mikrowellenhintergrunds interessiert, da diese Methoden nicht-Gaußsche Eigenschaften in der Verteilung des kosmischen Mikrowellenhintergrunds im Weltraum erkennen können, was wichtige Auswirkungen auf Theorien des frühen Universums hat. Dieser analytische Ansatz muss auch auf astronomische Auflösung skalierbar sein. Wir zeigen, dass unser Streunetzwerk diese Anforderungen erfüllt, indem wir CMB-Simulationen als Gaußsche oder nicht-Gaußsche Simulationen mit einer Auflösung von L = 1024 klassifizieren. Das Streunetzwerk hat diese Simulationen erfolgreich mit einer Genauigkeit von 95,3 % klassifiziert, was viel besser ist als die 53,1 %, die das herkömmliche sphärische CNN mit niedriger Auflösung erreicht.
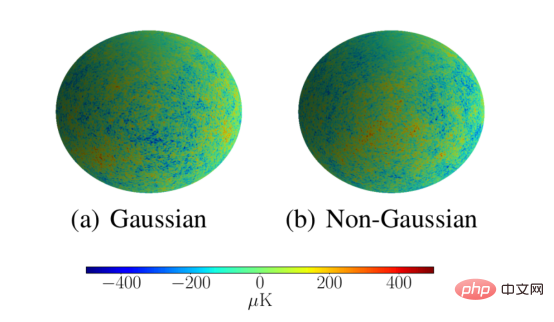
Die obige Abbildung zeigt hochauflösende Simulationsbeispiele von Gaußschen und nicht-Gaußschen CMBs zur Bewertung der Fähigkeit sphärischer Streunetzwerke, auf hohe Auflösungen zu skalieren.
Zusammenfassung
In diesem Artikel haben wir die Fähigkeit sphärischer Streuschichten untersucht, die Dimensionalität ihrer Eingabedarstellungen zu komprimieren und gleichzeitig wichtige Informationen für nachgelagerte Aufgaben zu bewahren. Wir haben gezeigt, dass Streuschichten dadurch für hochauflösende Kugelklassifizierungsaufgaben sehr nützlich sind. Dies öffnet die Tür zu bisher unlösbaren potenziellen Anwendungen wie der Analyse kosmologischer Daten und der hochauflösenden 360-Grad-Bild-/Videoklassifizierung. Viele Computer-Vision-Probleme wie Segmentierung oder Tiefenschätzung, die dichte Vorhersagen erfordern, erfordern jedoch sowohl eine hochdimensionale Ausgabe als auch eine hochdimensionale Eingabe. Schließlich ist die Frage, wie steuerbare sphärische CNN-Schichten entwickelt werden können, die die Dimensionalität der Ausgabedarstellung erhöhen und gleichzeitig die gleiche Varianz beibehalten können, ein aktuelles Forschungsthema der Kagenova-Entwickler. Diese werden im nächsten Artikel behandelt.
Referenzen
[1]Cobb, Wallis, Mavor-Parker, Marignier, Price, d'Avezac, McEwen, Efficient Generalized Spherical CNNs, ICLR (2021), arXiv:2010.11661
[2] Co Henne, Geiger, Koehler, Welling, Spherical CNNs, ICLR (2018), arXiv:1801.10130
[3] Esteves, Allen-Blanchette, Makadia, Daniilidis, Learning SO(3) Equivariante Representations with Spherical CNNs, ECCV (2018), arXiv:1711.06721
[4] McEwen, Jason, Wallis, Christopher und Mavor-Parker, Augustine N., Scattering Networks on the Sphere for Scalable and Rotationally Equivariant Spherical CNNs, ICLR (2022), arXiv:2102.02828
[5] Bruna, Joan und Stéphane Mallat, Invariant Scattering Convolution Networks, IEEE Transaction on Pattern Analysis and Machine Intelligence (2013)
[6] Perlmutter, Michael et al., Geometrische Wavelet-Streuungsnetzwerke auf kompaktem Riemannian Mannigfaltigkeiten, mathematisches und wissenschaftliches maschinelles Lernen. PMLR (2020), arXiv:1905.10448
Einführung des Übersetzers
Zhu Xianzhong, 51CTO-Community-Redakteur, 51CTO-Expertenblogger, Dozent, Computerlehrer an einer Universität in Weifang, ein Veteran in der freiberuflichen Tätigkeit Stücke aus der Programmierindustrie.
Originaltitel: Scaling Spherical Deep Learning to High-Resolution Input Data, Autor: Jason McEwen, Augustine Mavor-Parker
Das obige ist der detaillierte Inhalt vonSkalierung von sphärischem Deep Learning auf hochauflösende Eingabedaten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
 Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Heute diskutieren wir darüber, wie Deep-Learning-Technologie die Leistung von visionbasiertem SLAM (Simultaneous Localization and Mapping) in komplexen Umgebungen verbessern kann. Durch die Kombination von Methoden zur Tiefenmerkmalsextraktion und Tiefenanpassung stellen wir hier ein vielseitiges hybrides visuelles SLAM-System vor, das die Anpassung in anspruchsvollen Szenarien wie schlechten Lichtverhältnissen, dynamischer Beleuchtung, schwach strukturierten Bereichen und starkem Jitter verbessern soll. Unser System unterstützt mehrere Modi, einschließlich erweiterter Monokular-, Stereo-, Monokular-Trägheits- und Stereo-Trägheitskonfigurationen. Darüber hinaus wird analysiert, wie visuelles SLAM mit Deep-Learning-Methoden kombiniert werden kann, um andere Forschungen zu inspirieren. Durch umfangreiche Experimente mit öffentlichen Datensätzen und selbst abgetasteten Daten demonstrieren wir die Überlegenheit von SL-SLAM in Bezug auf Positionierungsgenauigkeit und Tracking-Robustheit.
 Verstehen Sie in einem Artikel: die Zusammenhänge und Unterschiede zwischen KI, maschinellem Lernen und Deep Learning
Mar 02, 2024 am 11:19 AM
Verstehen Sie in einem Artikel: die Zusammenhänge und Unterschiede zwischen KI, maschinellem Lernen und Deep Learning
Mar 02, 2024 am 11:19 AM
In der heutigen Welle rasanter technologischer Veränderungen sind künstliche Intelligenz (KI), maschinelles Lernen (ML) und Deep Learning (DL) wie helle Sterne und führen die neue Welle der Informationstechnologie an. Diese drei Wörter tauchen häufig in verschiedenen hochaktuellen Diskussionen und praktischen Anwendungen auf, aber für viele Entdecker, die neu auf diesem Gebiet sind, sind ihre spezifische Bedeutung und ihre internen Zusammenhänge möglicherweise noch immer rätselhaft. Schauen wir uns also zunächst dieses Bild an. Es ist ersichtlich, dass zwischen Deep Learning, maschinellem Lernen und künstlicher Intelligenz ein enger Zusammenhang und eine fortschreitende Beziehung besteht. Deep Learning ist ein spezifischer Bereich des maschinellen Lernens und des maschinellen Lernens
 Super stark! Top 10 Deep-Learning-Algorithmen!
Mar 15, 2024 pm 03:46 PM
Super stark! Top 10 Deep-Learning-Algorithmen!
Mar 15, 2024 pm 03:46 PM
Fast 20 Jahre sind vergangen, seit das Konzept des Deep Learning im Jahr 2006 vorgeschlagen wurde. Deep Learning hat als Revolution auf dem Gebiet der künstlichen Intelligenz viele einflussreiche Algorithmen hervorgebracht. Was sind Ihrer Meinung nach die zehn besten Algorithmen für Deep Learning? Im Folgenden sind meiner Meinung nach die besten Algorithmen für Deep Learning aufgeführt. Sie alle nehmen hinsichtlich Innovation, Anwendungswert und Einfluss eine wichtige Position ein. 1. Hintergrund des Deep Neural Network (DNN): Deep Neural Network (DNN), auch Multi-Layer-Perceptron genannt, ist der am weitesten verbreitete Deep-Learning-Algorithmus. Als er erstmals erfunden wurde, wurde er aufgrund des Engpasses bei der Rechenleistung in Frage gestellt Jahre, Rechenleistung, Der Durchbruch kam mit der Datenexplosion. DNN ist ein neuronales Netzwerkmodell, das mehrere verborgene Schichten enthält. In diesem Modell übergibt jede Schicht Eingaben an die nächste Schicht und
 So verwenden Sie CNN- und Transformer-Hybridmodelle, um die Leistung zu verbessern
Jan 24, 2024 am 10:33 AM
So verwenden Sie CNN- und Transformer-Hybridmodelle, um die Leistung zu verbessern
Jan 24, 2024 am 10:33 AM
Convolutional Neural Network (CNN) und Transformer sind zwei verschiedene Deep-Learning-Modelle, die bei verschiedenen Aufgaben eine hervorragende Leistung gezeigt haben. CNN wird hauptsächlich für Computer-Vision-Aufgaben wie Bildklassifizierung, Zielerkennung und Bildsegmentierung verwendet. Es extrahiert lokale Merkmale auf dem Bild durch Faltungsoperationen und führt eine Reduzierung der Merkmalsdimensionalität und räumliche Invarianz durch Pooling-Operationen durch. Im Gegensatz dazu wird Transformer hauptsächlich für Aufgaben der Verarbeitung natürlicher Sprache (NLP) wie maschinelle Übersetzung, Textklassifizierung und Spracherkennung verwendet. Es nutzt einen Selbstaufmerksamkeitsmechanismus, um Abhängigkeiten in Sequenzen zu modellieren und vermeidet so die sequentielle Berechnung in herkömmlichen rekurrenten neuronalen Netzen. Obwohl diese beiden Modelle für unterschiedliche Aufgaben verwendet werden, weisen sie Ähnlichkeiten in der Sequenzmodellierung auf
 AlphaFold 3 wird auf den Markt gebracht und sagt die Wechselwirkungen und Strukturen von Proteinen und allen Lebensmolekülen umfassend und mit weitaus größerer Genauigkeit als je zuvor voraus
Jul 16, 2024 am 12:08 AM
AlphaFold 3 wird auf den Markt gebracht und sagt die Wechselwirkungen und Strukturen von Proteinen und allen Lebensmolekülen umfassend und mit weitaus größerer Genauigkeit als je zuvor voraus
Jul 16, 2024 am 12:08 AM
Herausgeber | Rettichhaut Seit der Veröffentlichung des leistungsstarken AlphaFold2 im Jahr 2021 verwenden Wissenschaftler Modelle zur Proteinstrukturvorhersage, um verschiedene Proteinstrukturen innerhalb von Zellen zu kartieren, Medikamente zu entdecken und eine „kosmische Karte“ jeder bekannten Proteininteraktion zu zeichnen. Gerade hat Google DeepMind das AlphaFold3-Modell veröffentlicht, das gemeinsame Strukturvorhersagen für Komplexe wie Proteine, Nukleinsäuren, kleine Moleküle, Ionen und modifizierte Reste durchführen kann. Die Genauigkeit von AlphaFold3 wurde im Vergleich zu vielen dedizierten Tools in der Vergangenheit (Protein-Ligand-Interaktion, Protein-Nukleinsäure-Interaktion, Antikörper-Antigen-Vorhersage) deutlich verbessert. Dies zeigt, dass dies innerhalb eines einzigen einheitlichen Deep-Learning-Frameworks möglich ist
 TensorFlow Deep-Learning-Framework-Modell-Inferenzpipeline für Porträtausschnitt-Inferenz
Mar 26, 2024 pm 01:00 PM
TensorFlow Deep-Learning-Framework-Modell-Inferenzpipeline für Porträtausschnitt-Inferenz
Mar 26, 2024 pm 01:00 PM
Übersicht Um ModelScope-Benutzern die schnelle und bequeme Nutzung verschiedener von der Plattform bereitgestellter Modelle zu ermöglichen, wird eine Reihe voll funktionsfähiger Python-Bibliotheken bereitgestellt, die die Implementierung offizieller ModelScope-Modelle sowie die erforderlichen Tools für die Verwendung dieser Modelle für Inferenzen umfassen , Feinabstimmung und andere Aufgaben im Zusammenhang mit der Datenvorverarbeitung, Nachverarbeitung, Effektbewertung und anderen Funktionen und bietet gleichzeitig eine einfache und benutzerfreundliche API und umfangreiche Anwendungsbeispiele. Durch den Aufruf der Bibliothek können Benutzer Aufgaben wie Modellinferenz, Schulung und Bewertung erledigen, indem sie nur wenige Codezeilen schreiben. Auf dieser Basis können sie auch schnell eine Sekundärentwicklung durchführen, um ihre eigenen innovativen Ideen zu verwirklichen. Das derzeit von der Bibliothek bereitgestellte Algorithmusmodell ist:
 Erkunden Sie die Algorithmen und Prinzipien von Gestenerkennungsmodellen (erstellen Sie ein einfaches Trainingsmodell für die Gestenerkennung in Python).
Jan 24, 2024 pm 05:51 PM
Erkunden Sie die Algorithmen und Prinzipien von Gestenerkennungsmodellen (erstellen Sie ein einfaches Trainingsmodell für die Gestenerkennung in Python).
Jan 24, 2024 pm 05:51 PM
Die Gestenerkennung ist ein wichtiges Forschungsgebiet im Bereich Computer Vision. Sein Zweck besteht darin, die Bedeutung von Gesten durch die Analyse menschlicher Handbewegungen in Videostreams oder Bildsequenzen zu bestimmen. Die Gestenerkennung hat ein breites Anwendungsspektrum, wie z. B. gestengesteuerte Smart Homes, virtuelle Realität und Spiele, Sicherheitsüberwachung und andere Bereiche. In diesem Artikel werden die in Gestenerkennungsmodellen verwendeten Algorithmen und Prinzipien vorgestellt und mithilfe von Python ein einfaches Trainingsmodell für die Gestenerkennung erstellt. Von Gestenerkennungsmodellen verwendete Algorithmen und Prinzipien Die von Gestenerkennungsmodellen verwendeten Algorithmen und Prinzipien sind vielfältig, darunter Modelle, die auf Deep Learning, traditionellen Modellen des maschinellen Lernens, regelbasierten Methoden und traditionellen Bildverarbeitungsmethoden basieren. Die Prinzipien und Eigenschaften dieser Methoden werden im Folgenden vorgestellt. 1. Modellieren Sie Deep Learning basierend auf Deep Learning
 Was genau bedeutet Fehler im Restmodul?
Jan 23, 2024 am 11:00 AM
Was genau bedeutet Fehler im Restmodul?
Jan 23, 2024 am 11:00 AM
Das Restmodul ist eine häufig verwendete Technik beim Deep Learning, um die Probleme verschwindender und explodierender Gradienten zu lösen und die Genauigkeit und Stabilität des Modells zu verbessern. Sein Kern ist die Restverbindung, die Eingabedaten und Ausgabedaten hinzufügt, um eine schichtübergreifende Verbindung zu bilden, wodurch das Modell leichter Restinformationen lernen kann. Fehler bezieht sich auf den Fehler an der Restverbindung. Im Folgenden wird dieses Konzept im Detail erläutert. Beim Deep Learning bezieht sich Fehler normalerweise auf die Differenz zwischen dem vorhergesagten Wert der Trainingsdaten und dem wahren Wert, auch bekannt als Verlust. Im Restmodul unterscheidet sich die Fehlerberechnungsmethode von der des normalen neuronalen Netzwerkmodells und umfasst die folgenden zwei Aspekte: 1. Restberechnungsfehler Die Restverbindung im Restmodul wird durch Addition der Eingabedaten und Ausgabedaten erreicht. schichtübergreifende Verbindungen. An der Residuenverbindung müssen wir das Residuum berechnen



