 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Theoretischer Informatiker Boaz Barak: Deep Learning ist keine „einfache Statistik', und die beiden entfernen sich immer weiter
Theoretischer Informatiker Boaz Barak: Deep Learning ist keine „einfache Statistik', und die beiden entfernen sich immer weiter
Theoretischer Informatiker Boaz Barak: Deep Learning ist keine „einfache Statistik', und die beiden entfernen sich immer weiter
In den 1990er Jahren entwickelte Rob Tibshirani, ein bekannter Professor für Bioinformatik an der Stanford University, ein Vokabular, um eine einfache und grobe Entsprechung zwischen verschiedenen Konzepten im maschinellen Lernen und in der Statistik herzustellen:

Einerseits Einerseits vermittelt diese Tabelle ein grundlegendes Verständnis des maschinellen Lernens, fasst aber gleichzeitig einfach die Konzepte des Deep Learning bzw. des maschinellen Lernens in Wortbedeutungen in der Statistik zusammen, was bei den meisten Menschen auch Zweifel an der Natur des Deep Learning weckt : Deep Learning ist „einfache Statistik“.
Allerdings hat eine solche Wahrnehmung in der eingehenden Diskussion die Forscher bis zu einem gewissen Grad daran gehindert, die wesentlichen Gründe für den Erfolg von Deep Learning zu verstehen. In einem Artikel „Die unruhige Beziehung zwischen Deep Learning und (klassischer) Statistik“ vom Juni dieses Jahres verglich und unterschied Boaz Barak, ein bekannter Harvard-Professor und theoretischer Informatiker, Deep Learning und Statistik und wies auf die Grundlagen des Deep Learning hin . Die konstituierenden Faktoren unterscheiden sich stark von der Statistik.
Boaz Barak machte eine wichtige Beobachtung: Wenn sich das Modell auf Vorhersage und Beobachtung konzentriert, ist ein Deep-Learning-Modell mit Black-Box-Eigenschaften möglicherweise die beste Wahl Wenn Sie die Ursache und Wirkung von Dingen verstehen und die Interpretierbarkeit verbessern, können „einfache“ Modelle möglicherweise eine bessere Leistung erbringen. Dies deckt sich mit der Idee der „Einfachheit“, die eines der beiden Prinzipien der Intelligenz darstellt, die letzten Monat von drei Wissenschaftlern vorgeschlagen wurden: Ma Yi, Cao Ying und Shen Xiangyang.
Gleichzeitig diskutierte Boaz Barak die Kompatibilität mit Deep Learning, indem er zwei verschiedene Szenariofälle der Anpassung statistischer Modelle und des Lernens von Mathematik zeigte. Er glaubte, dass die Mathematik und der Code des Deep Learning zwar nichts mit der Anpassung der Statistik zu tun haben; Das Modell ist fast das gleiche, aber auf einer tieferen Ebene kann ein großer Teil des Deep Learning im Szenario „Fähigkeiten für Schüler vermitteln“ erfasst werden.
Statistisches Lernen spielt beim Deep Learning eine wichtige Rolle, daran besteht kein Zweifel. Sicher ist jedoch, dass die statistische Perspektive kein vollständiges Bild zum Verständnis von Deep Learning liefern kann. Um verschiedene Aspekte von Deep Learning zu verstehen, müssen Menschen immer noch aus unterschiedlichen Perspektiven an die Sache herangehen.
Das Folgende ist Boaz Baraks Diskussion:
1 Vorhersage und Erklärung bei der Modellanpassung
Seit Tausenden von Jahren passen Wissenschaftler Modelle an Beobachtungen an. Beispielsweise schlug der ägyptische Astronom Ptolemäus, wie im Buchcover von Philosophy of Science erwähnt, ein geniales Modell der Planetenbewegung vor. Das Modell von Ptolemäus war geozentrisch (d. h. die Planeten drehten sich um die Erde), verfügte jedoch über eine Reihe von „Knöpfen“ (insbesondere Epizyklen), die ihm eine hervorragende Vorhersagegenauigkeit verliehen. Im Gegensatz dazu ging Kopernikus‘ ursprüngliches heliozentrisches Modell von kreisförmigen Umlaufbahnen der Planeten um die Sonne aus. Es ist einfacher (weniger „abstimmbare Knöpfe“) und insgesamt korrekter als das Modell von Ptolemäus, aber weniger genau bei der Vorhersage von Beobachtungen . (Kopernikus fügte später auch seine eigenen Epizyklen hinzu, wodurch sie mit der Leistung von Ptolemäus vergleichbar wurden.)
Ptolemäische und kopernikanische Modelle sind beispiellos. Wenn Sie eine „Black Box“ benötigen, um Vorhersagen zu treffen, ist das ptolemäische geozentrische Modell überlegen. Und wenn Sie ein einfaches Modell suchen, das einen „Blick ins Innere“ ermöglicht und als theoretischer Ausgangspunkt für die Erklärung der Bewegung der Sterne dient, dann ist das Modell von Kopernikus besser.
Tatsächlich verfeinerte Kepler schließlich das Modell von Kopernikus zu elliptischen Bahnen und schlug seine drei Gesetze der Planetenbewegung vor, die es Newton ermöglichten, sie mit denselben Gesetzen der Schwerkraft zu erklären, die auf der Erde gelten. Dazu ist es entscheidend, dass das heliozentrische Modell nicht nur eine „Black Box“ ist, die Vorhersagen liefert, sondern durch einfache mathematische Gleichungen mit wenigen „beweglichen Teilen“ gegeben ist. Die Astronomie ist seit vielen Jahren eine Inspirationsquelle für die Entwicklung statistischer Techniken. Gauß und Legendre erfanden (unabhängig voneinander) um 1800 die Regression der kleinsten Quadrate zur Vorhersage der Umlaufbahnen von Asteroiden und anderen Himmelskörpern. Auch Cauchys Erfindung des Gradientenabstiegs im Jahr 1847 war auf astronomische Vorhersagen zurückzuführen.
In der Physik können Sie (zumindest manchmal) „alles haben“ – finden Sie die „richtige“ Theorie, die Ihnen die beste Vorhersagegenauigkeit und die beste Erklärung Ihrer Daten bietet, wie Ideen wie „Occams Rasiermesser erfasst“ und die Einfachheit der Annahme belegen , Vorhersagekraft und erklärende Einsicht stimmen alle miteinander überein. In vielen anderen Bereichen besteht jedoch eine Spannung zwischen den beiden Zielen Erklärung (oder allgemeiner Einsicht) und Vorhersage. Wenn Sie nur Beobachtungen vorhersagen möchten, ist eine „Black Box“ möglicherweise die beste Wahl. Wenn Sie jedoch kausale Modelle, allgemeine Prinzipien oder wichtige Merkmale extrahieren, ist ein einfaches Modell, das leicht zu verstehen und zu erklären ist, möglicherweise besser.
Die richtige Wahl des Modells hängt von seinem Einsatzzweck ab. Betrachten Sie beispielsweise einen Datensatz, der die Genexpression und Phänotypen vieler Personen enthält (z. B. für eine bestimmte Krankheit). Wenn das Ziel darin besteht, die Wahrscheinlichkeit einer Erkrankung einer Person vorherzusagen, möchte man häufig das beste Modell für die Aufgabe verwenden , egal wie komplex oder von wie vielen Genen es abhängt. Wenn Ihr Ziel hingegen darin besteht, einige Gene für die weitere Untersuchung in einem Nasslabor zu identifizieren, wird eine hochentwickelte Blackbox nur begrenzt nützlich sein, selbst wenn sie sehr genau ist.
Im Jahr 2001 erläuterte Leo Breiman diesen Punkt wirkungsvoll in seinem berühmten Artikel „Statistische Modellierung: Die zwei Kulturen“ über statistische Modellierung. „Datenmodellierungskultur“ konzentriert sich auf einfache generative Modelle, die die Daten erklären, während „Algorithmenmodellierungskultur“ nicht versteht, wie die Daten generiert werden, sondern sich darauf konzentriert, Modelle zu finden, die die Daten vorhersagen können. Breiman glaubt, dass die Statistik zu sehr von der Primärkultur dominiert wird und dass dieser Fokus „zu irrelevanten Theorien und fragwürdigen wissenschaftlichen Schlussfolgerungen führt“ und „Statistiker daran hindert, spannende neue Fragen zu untersuchen.“
Allerdings ist Breimans Artikel umstritten. Während Brad Efron einigen Ansichten zustimmt: „Auf den ersten Blick scheint Leo Breimans spannendes Papier Einfachheit und wissenschaftliche Erkenntnisse zugunsten einer Black Box mit vielen zu manipulierenden Knöpfen abzulehnen. Auf den zweiten Blick ist es immer noch so.“ Dasselbe." Aber in einem kürzlich erschienenen Artikel („Prediction, Estimation, and Attribution“) gab Efron großzügig zu, dass „es sich herausstellte, dass Breiman vorausschauender war als ich: Reine Vorhersagealgorithmen haben im 21. Jahrhundert und ihrer Entwicklung im Rampenlicht der Statistik gestanden.“ Die Richtung ähnelt so ziemlich dem, was Leo zuvor erwähnt hat auf Vorhersagen ausgerichtet Diese Kultur gibt es schon seit langer Zeit. Beispielsweise sind Duda und Harts Lehrbuch „Deconstructing Distributions: A Pointwise Framework of Learning“ aus dem Jahr 1973 und Highleymans Aufsatz „The Design and Analysis of Pattern Recognition Experiments“ aus dem Jahr 1962 für heutige Deep-Learning-Praktiker sehr gut bekannt:
In ähnlicher Weise finden Highleymans handgeschriebener Zeichendatensatz und Chow, die Architektur, die dazu verwendet wurde (~58 % Genauigkeit), auch bei modernen Lesern großen Anklang.

Warum ist Deep Learning anders?
1992 verfassten Stuart Geman, Elie Bienenstock und Rene Doursat gemeinsam einen Artikel mit dem Titel „Neuronale Netze und das Bias/Varian-Dilemma“, in dem es um einige pessimistische Ansichten ging, zum Beispiel „Aktuelle Feedforward-Neuronale Netze“, „Netze, sind weitgehend unzureichend, um schwierige Probleme der maschinellen Wahrnehmung und des maschinellen Lernens zu lösen“; insbesondere argumentieren sie, dass universelle neuronale Netze schwierige Aufgaben nicht erfolgreich lösen können und der einzige Weg für neuronale Netze zum Erfolg in handgefertigten Funktionen bestehe. In ihren Worten: „Wichtige Funktionen müssen eingebaut oder ‚fest verdrahtet‘ sein … und nicht durch statistische Methoden gelernt werden.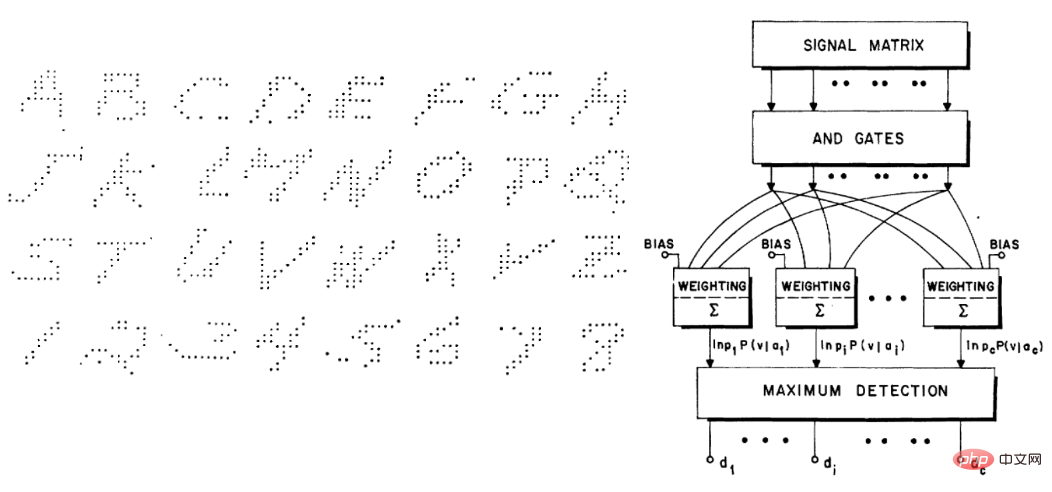
“ Im Nachhinein liegen sie völlig falsch. Darüber hinaus waren moderne neuronale Netzwerkarchitekturen wie Transformer sogar noch vielseitiger als damalige Faltungsnetzwerke. Aber es ist interessant, die Gründe für ihre Fehler zu verstehen.
Ich denke, der Grund, warum sie den Fehler gemacht haben, ist, dass Deep Learning sich tatsächlich von anderen Lernmethoden unterscheidet. Ein A-priori-Phänomen ist: Deep Learning scheint nur noch ein weiteres Vorhersagemodell zu haben, wie „nächster Nachbar“ oder „Random Forest“. Es mag mehr „Noppen“ haben, aber das scheint eher ein quantitativer als ein qualitativer Unterschied zu sein. Mit den Worten von PW Andreson: „Mehr ist anders“.
Sobald sich in der Physik die Skala um mehrere Größenordnungen ändert, brauchen wir oft nur eine völlig andere Theorie, um sie zu erklären, und das Gleiche gilt für Deep Learning. Tatsächlich funktioniert Deep Learning völlig anders als klassische Modelle (parametrisch oder nicht parametrisch), auch wenn die Gleichungen (und der Python-Code) aus einer übergeordneten Perspektive gleich aussehen.
Um dies zu erklären, schauen wir uns den Lernprozess von zwei sehr unterschiedlichen Beispielen an: Anpassen eines statistischen Modells und Unterrichten der Schüler, Mathematik zu lernen.
Szenario A: Anpassen eines statistischen Modells
Im Allgemeinen sind die Schritte zum Anpassen eines statistischen Modells an Daten wie folgt:
1 Wir beobachten einige Daten x und y. x kann als Matrix von n betrachtet werden. Der Einfachheit halber wird additives Rauschen verwendet und 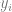 ist die korrekte wahre Bezeichnung. )
ist die korrekte wahre Bezeichnung. ) 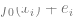 2. Durch die Ausführung eines Optimierungsalgorithmus können wir das Modell
2. Durch die Ausführung eines Optimierungsalgorithmus können wir das Modell 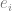 an die Daten anpassen und so das empirische Risiko von
an die Daten anpassen und so das empirische Risiko von 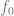 minimieren. Das heißt, wir verwenden einen Optimierungsalgorithmus, um die minimierte Anzahl von
minimieren. Das heißt, wir verwenden einen Optimierungsalgorithmus, um die minimierte Anzahl von
zu finden, wobei 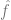 ein Verlustterm ist (der erfasst, wie nahe
ein Verlustterm ist (der erfasst, wie nahe 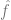 an y liegt) und
an y liegt) und 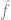 ein optionaler Normalisierungsterm ist (der versucht, zu verzerren).
ein optionaler Normalisierungsterm ist (der versucht, zu verzerren). 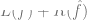 hin zu einfacheren Modellen).
hin zu einfacheren Modellen). 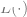
3. Wir hoffen, dass unser Modell einen guten Gesamtverlust aufweisen kann, da der Generalisierungsfehler/-verlust 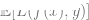 gering ist (diese Vorhersage basiert auf Experimenten aus dem Gesamtdaten, in denen sich die Daten befinden).
gering ist (diese Vorhersage basiert auf Experimenten aus dem Gesamtdaten, in denen sich die Daten befinden).
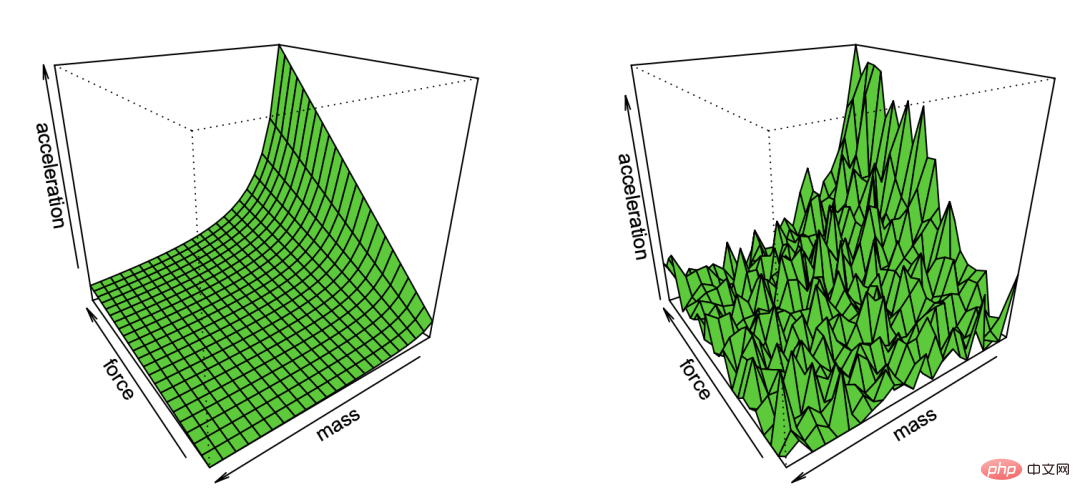
Illustration: Newtons erstes Gesetz, reproduziert von Bradley Efron durch die Beobachtung von Lärm Comic #🎜🎜 #
Dieses sehr allgemeine Paradigma umfasst viele Einstellungen, einschließlich linearer Regression der kleinsten Quadrate, nächste Nachbarn, Training neuronaler Netzwerke und mehr. In einer klassischen statistischen Umgebung würden wir Folgendes erwarten: . (Wenn wir uns in einer nicht-konvexen Umgebung befinden und/oder einen Regularisiererterm haben, können wir F als die Menge solcher Modelle annehmen, die vom Algorithmus mit nicht vernachlässigbarer Wahrscheinlichkeit implementiert werden können, angesichts der Auswirkungen der Algorithmuswahl und des Regularisierers. ) Die Abweichung von
F ist die beste Annäherung an die richtige Bezeichnung und kann durch das Element erreicht werden. Je größer die Klasse F, desto kleiner die Abweichung. Bei
kann die Abweichung sogar Null sein. Wenn die F-Klasse jedoch größer ist, sind mehr Stichproben erforderlich, um ihren Zugehörigkeitsbereich einzugrenzen, und daher ist die Varianz im Algorithmus-Ausgabemodell größer. Der gesamte Generalisierungsfehler ist die Summe aus Bias-Term und Varianzbeitrag. 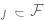 Daher weist statistisches Lernen häufig einen Kompromiss zwischen Bias und Varianz auf und minimiert den Gesamtfehler durch eine „Goldlöckchen-Wahl“ der korrekten Modellkomplexität. Tatsächlich tun Geman et al. genau das und rechtfertigen ihren Pessimismus gegenüber neuronalen Netzen damit, dass „die grundlegenden Einschränkungen, die sich aus dem Bias-Varianz-Dilemma ergeben, für alle nichtparametrischen Inferenzmodelle, einschließlich neuronaler Netze, gelten.“
Daher weist statistisches Lernen häufig einen Kompromiss zwischen Bias und Varianz auf und minimiert den Gesamtfehler durch eine „Goldlöckchen-Wahl“ der korrekten Modellkomplexität. Tatsächlich tun Geman et al. genau das und rechtfertigen ihren Pessimismus gegenüber neuronalen Netzen damit, dass „die grundlegenden Einschränkungen, die sich aus dem Bias-Varianz-Dilemma ergeben, für alle nichtparametrischen Inferenzmodelle, einschließlich neuronaler Netze, gelten.“ 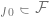
Beim statistischen Lernen führt der Erhalt von mehr Funktionen oder Daten nicht unbedingt zu einer Leistungsverbesserung. Zum Beispiel ist das Lernen aus Daten, die viele irrelevante Merkmale enthalten, eine größere Herausforderung. Ebenso ist das Lernen aus einem Mischungsmodell, bei dem die Daten aus einer von zwei Verteilungen stammen (z. B.
und ), besser als Lernen ein einzelner unabhängig voneinander Härter.  Rückläufige Erträge.
Rückläufige Erträge.  In vielen Fällen erfordert die Reduzierung des Vorhersagerauschens auf einen bestimmten Parameter
In vielen Fällen erfordert die Reduzierung des Vorhersagerauschens auf einen bestimmten Parameter
#🎜 unter einem bestimmten Parameter k liegt Die Formerweiterung von 🎜#. In diesem Fall sind etwa k Stichproben erforderlich, um „durchzustarten“, und sobald Sie dies getan haben, werden Sie mit einem System abnehmender Erträge konfrontiert sein, d Um die Genauigkeit auf 95 % zu erhöhen, sind noch ca. 3n Punkte nötig. Im Allgemeinen möchten wir mit zunehmenden Ressourcen (ob Daten, Modellkomplexität oder Berechnung) detailliertere Unterscheidungen erfassen, anstatt neue qualitative Fähigkeiten freizuschalten. Datenpunkte haben keine natürliche „Schwierigkeit“ (zumindest in einigen Fällen). Traditionell wird angenommen, dass Datenpunkte unabhängig von einer bestimmten Verteilung abgetastet werden. Obwohl Punkte in der Nähe der Entscheidungsgrenze aufgrund der hochdimensionalen Konzentration der Messungen möglicherweise schwieriger zu klassifizieren sind, wird erwartet, dass die meisten Punkte ähnliche Abstände haben. Daher ist zumindest bei klassischen Datenverteilungen nicht zu erwarten, dass sich die Schwierigkeitsgrade der Punkte stark unterscheiden. Allerdings können gemischte Modelle unterschiedliche Schwierigkeitsgrade dieses Unterschieds aufweisen, so dass dieser Unterschied im Gegensatz zu den anderen oben genannten Problemen in einem statistischen Umfeld nicht sehr überraschend wäre. Lassen Sie uns im Gegensatz zum oben Gesagten darüber sprechen, den Schülern einige spezifische mathematische Themen beizubringen (z. B. die Berechnung von Ableitungen). Geben Sie ihnen regelmäßig Anweisungen und Übungen. Dies ist kein formal definierter Rahmen, aber einige seiner qualitativen Merkmale können berücksichtigt werden: Hinweis: Übungsübungen zum Erlernen spezifischer Mathematikfähigkeiten von der IXL-Website In diesem Fall erlernen die Schüler eine Fertigkeit und nicht einen Mengenschätzer/-prädiktor. Während die Definition von „Fähigkeiten“ keine triviale Aufgabe ist, handelt es sich doch um ein Ziel ganz anderer Art. Auch wenn Funktionszuordnungsübungen nicht als „Black Box“ zur Lösung einiger relevanter Aufgaben Je mehr, desto besser. Im Allgemeinen erzielen Schüler bessere Ergebnisse, wenn sie mehr Fragen und verschiedene Arten von Fragen üben. Aber tatsächlich hat die „hybride Modellierung“ – die Lösung einiger Rechenaufgaben und einiger Algebraaufgaben – keinen Einfluss auf die Leistungen der Schüler in der Analysis und hilft ihnen tatsächlich beim Lernen. Während die Erfolge bei der Lösung von Problemen irgendwann abnehmen, scheinen die Schüler Phasen zu durchlaufen, in denen das Lösen von Problemen dazu beiträgt, dass Konzepte „klicken“ und neue Funktionen freischalten. Wenn Schüler eine bestimmte Art von Problem wiederholen, scheinen sich darüber hinaus ihre Fähigkeiten und die Darstellung dieser Probleme auf ein niedrigeres Niveau zu verlagern, was es ihnen ermöglicht, bei diesen Problemen eine gewisse Automatisierung zu entwickeln, die sie vorher nicht hatten. Es gibt mehr als eine Möglichkeit, mathematische Konzepte zu vermitteln, und selbst wenn Schüler mit unterschiedlichen Büchern, Lehrmethoden oder Bewertungssystemen lernen, lernen sie am Ende immer noch denselben Stoff und ähnliche interne Darstellungen. Bei Mathematikübungen können wir oft einen starken Zusammenhang zwischen den Methoden erkennen, die verschiedene Schüler zur Lösung desselben Problems verwenden. Die Schwierigkeit eines Problems scheint festgelegt zu sein, und auch die Reihenfolge der Lösung der Probleme ist festgelegt, wodurch der Lernprozess optimiert werden kann. Genau das tun Plattformen wie IXL. 4 Welche der beiden oben genannten Metaphern beschreibt also modernes Deep Learning besser und warum ist es insbesondere so erfolgreich? Die statistische Modellanpassung scheint besser mit Mathematik und Code übereinzustimmen. Tatsächlich trainiert die standardmäßige Pytorch-Trainingsschleife tiefe Netzwerke durch empirische Risikominimierung, wie oben beschrieben: 🎜🎜# Auf einer tieferen Ebene ist die Beziehung zwischen diesen beiden Einstellungen jedoch nicht so klar. Konkret kann dies durch Reparieren einer bestimmten Lernaufgabe und Verwenden der Methode „Selbstüberwachtes Lernen + lineare Sonde“ zum Trainieren des Klassifizierungsalgorithmus erfolgen. Das Algorithmustraining ist wie folgt: #🎜 🎜# 1. Angenommen, die Daten sind eine Sequenz 2. Finden Sie zunächst ein tiefes neuronales Netzwerk zur Darstellung der Funktion (wobei C die Anzahl der Klassen ist), wodurch der Kreuzentropieverlust minimiert wird. Der endgültige Klassifikator ergab eine Zuordnung von Je mehr, desto besser. Beim selbstüberwachten Lernen verbessert sich die Qualität der Darstellung mit zunehmender Datenmenge. Und je vielfältiger die Daten, desto besser. Hinweis: Datensatz des Google PaLM-Modells # 🎜 🎜# Fähigkeiten freischalten. Da die Ressourcen (Daten, Berechnung, Modellgröße) zunehmen, sind immer wieder diskontinuierliche Verbesserungen bei Deep-Learning-Modellen zu beobachten, und dies wurde auch in einigen synthetischen Umgebungen gezeigt. Bildunterschrift: Mit zunehmender Modellgröße zeigt das PaLM-Modell in einigen Benchmarks einige diskrete Verbesserungen (in der obigen Abbildung gibt es nur drei Größenvorbehalte) und schaltet einige überraschende Funktionen frei, wie z. B. „Erkläre den Witz“. Die Leistung ist weitgehend unabhängig von Verlusten oder Daten. Mehr als ein selbstüberwachter Verlust, mehrere kontrastive und rekonstruktive Verluste werden für Bilder verwendet. Sprachmodelle verwenden manchmal eine einseitige Rekonstruktion (Vorhersage des nächsten Tokens) und verwenden manchmal Maskierungsmodelle, deren Ziel darin besteht, maskierte Eingaben vom linken und rechten Token vorherzusagen. Es ist auch möglich, einen etwas anderen Datensatz zu verwenden, was sich auf die Effizienz auswirken kann, aber solange „vernünftige“ Entscheidungen getroffen werden, ist die ursprüngliche Ressource im Allgemeinen aussagekräftiger für die Leistung als der spezifische Verlust oder der verwendete Datensatz. Einige Fälle sind schwieriger als andere. Dies ist nicht auf selbstüberwachtes Lernen beschränkt, Datenpunkte können einen gewissen inhärenten „Schwierigkeitsgrad“ aufweisen. Tatsächlich gibt es mehrere praktische Beweise dafür, dass verschiedene Lernalgorithmen unterschiedliche „Fähigkeitsstufen“ und unterschiedliche Punkte unterschiedliche „Schwierigkeitsstufen“ haben (die Wahrscheinlichkeit, dass der Klassifikator f x richtig klassifiziert, Die Fähigkeit von f steigt um eins Richtung, und die Schwierigkeit von x nimmt in eine Richtung ab). Das Paradigma „Fähigkeit und Schwierigkeit“ ist die klarste Erklärung des von Recht und Miller et al. entdeckten Phänomens der „Online-Genauigkeit“, und in dem Artikel, den ich gemeinsam mit Kaplun, Ghosh, Garg und Nakkiran verfasst habe, zeige ich das auch Der Datensatz Wie unterschiedliche Eingaben eine inhärente „Schwierigkeitssignatur“ aufweisen, die herkömmlicherweise gegenüber verschiedenen Modellen robust zu sein scheint. Bildunterschrift: Miller et al.s Diagramm, das die Genauigkeit von Linienphänomenen für einen auf CIFAR-10 trainierten und auf CINIC-10 getesteten Klassifikator zeigt Bildunterschrift: Dekonstruieren Sie den Datensatz in verschiedene „Schwierigkeitsprofil“-Punkte aus dem Artikel „Deconstructing Distributions: A Pointwise Framework of Learning“ von Kaplun und Ghosh et al., um eine zunehmende Anzahl von Ressourcenklassifikatoren zu erhalten. Das obere Diagramm zeigt verschiedene Softmax-Wahrscheinlichkeiten für die wahrscheinlichste Klasse als Funktion der globalen Genauigkeit eines Klassifikators für eine Klasse, indiziert nach Trainingszeit; das untere Kreisdiagramm zeigt die Aufteilung verschiedener Datensätze in verschiedene Punkttypen. Bemerkenswerterweise ist diese Zerlegung für verschiedene neuronale Architekturen ähnlich. Training ist Lehren. Modernes Training großer Modelle ähnelt eher dem Unterrichten von Schülern, als dass sich das Modell an die Daten anpassen lässt, „Pausen“ einlegt oder andere Methoden ausprobiert, wenn die Schüler es nicht verstehen oder müde wirken (Trainingsabweichung). Die Trainingsprotokolle für das große Modell von Meta sind aufschlussreich – neben Hardwareproblemen kann man auch einige Eingriffe sehen, wie z. B. das Wechseln verschiedener Optimierungsalgorithmen während des Trainings und sogar die Erwägung von „Hot-Swapping“-Aktivierungsfunktionen (GELU zu RELU). Letzteres macht wenig Sinn, wenn man sich das Modelltraining als Anpassung von Daten und nicht als Lernen einer Darstellung vorstellt. Bildunterschrift: Auszug aus Metas TrainingsprotokollZwei Fälle werden im Folgenden besprochen: Bisher haben wir nur über selbstüberwachtes Lernen gesprochen, aber das Ein typisches Beispiel für Deep Learning ist immer noch das überwachte Lernen. Schließlich kommt der „ImageNet-Moment“ des Deep Learning von ImageNet. Gilt also das, was wir oben besprochen haben, auch für überwachtes Lernen? Erstens: Die Entstehung von überwachtem Deep Learning in großem Maßstab ist dank der Verfügbarkeit großer, qualitativ hochwertiger gekennzeichneter Datensätze (z. B. ImageNet) gewissermaßen ein historischer Zufall. Man kann sich eine alternative Geschichte vorstellen: Deep Learning erzielte zunächst Durchbrüche bei der Verarbeitung natürlicher Sprache durch unbeaufsichtigtes Lernen und gelangte erst dann zu Vision und überwachtem Lernen. Zweitens gibt es Hinweise darauf, dass sich überwachtes Lernen „hinter den Kulissen“ ähnlich verhält, obwohl es völlig andere Verlustfunktionen verwendet als selbstüberwachtes Lernen. Beide erzielen in der Regel die gleiche Leistung. In der Arbeit „Revisiting Model Stitching to Compare Neural Representations“ wurde auch festgestellt, dass sie ähnliche interne Darstellungen gelernt haben. Konkret kann man für jedes Bildunterschrift: Tabelle aus der Arbeit des Hinton-Teams „Big Self-Supervised Models are Strong Semi-Supervised Learners“. Beachten Sie die allgemeine Leistungsähnlichkeit zwischen überwachtem Lernen, Feinabstimmung (100 %) selbstüberwacht und selbstüberwachter + linearer Erkennung Bildunterschrift: Auszug aus dem Artikel „Revisiting Model Stitching to Compare Neural Representations“. „Supervision und Supervisionsmodelle. Links – Wenn das selbstüberwachte Modell 3 % weniger genau ist als das überwachte Modell, führt eine vollständig kompatible Darstellung zu einer Spleißeinbuße von p 3 % (wenn p Schichten aus dem selbstüberwachten Modell stammen). Wenn die Modelle völlig inkompatibel sind, ist mit einem drastischen Rückgang der Genauigkeit zu rechnen, je mehr Modelle zusammengefügt werden. Rechts – Tatsächliche Ergebnisse des Spleißens verschiedener selbstüberwachter Modelle. Der Vorteil selbstüberwachter + einfacher Modelle besteht darin, dass sie Feature-Learning oder „Deep-Learning-Magie“ (Ergebnisse tiefer Darstellungsfunktionen) mit statistischer Modellanpassung (durchgeführt durch lineare oder andere „einfache“ Klassifikatoren) kombinieren können. oberhalb dieser Darstellung getrennt). Abschließend kann die Tatsache, dass „Meta-Learning“ im Allgemeinen mit Lerndarstellungen gleichgesetzt zu werden scheint, auch wenn sie spekulativ ist (Einzelheiten finden Sie im Artikel „Rapid Learning or Feature Reuse? Towards Understanding the Effectiveness of MAML“) sein Dies wird als weiterer Beweis zur Unterstützung der Ideen dieses Artikels angesehen, unabhängig davon, wofür das Modell angeblich optimiert wird. Leser haben vielleicht bemerkt, dass ich die typischen Beispiele für Unterschiede zwischen statistischen Lernmodellen und Deep-Learning-Modellen in praktischen Anwendungen übersprungen habe, nämlich das Fehlen eines „Bias-Varianz-Kompromisses“ und Überparametrisierung Die hervorragende Generalisierungsfähigkeit des Modells. Es gibt zwei Gründe, warum ich nicht im Detail auf diese Beispiele eingehen werde: Erstens: Wenn überwachtes Lernen tatsächlich mit Selbstüberwachung + einfachem Lernen auf „niedrigerem Niveau“ gleichzusetzen ist, dann kann dies aufgrund seiner Generalisierungsfähigkeit der Fall sein erklärt werden (Einzelheiten finden Sie im Artikel „Für selbstüberwachtes Lernen impliziert Rationalität nachweislich eine Verallgemeinerung“); Das Besondere an tiefen Netzwerken ist nicht, dass sie im Vergleich zur Anzahl der Stichproben groß sind, sondern dass sie in absoluten Zahlen groß sind. Tatsächlich In unbeaufsichtigten/selbstüberwachten Lernmodellen gibt es normalerweise keine Überparametrisierung. Selbst für große Sprachmodelle verfügen sie lediglich über größere Datensätze, was ihre Leistung jedoch nicht weniger mysteriös macht. Bildunterschrift: In dem Artikel „The Deep Bootstrap Framework: Good Online Learners are Good Offline Generalizers“ zeigen die Ergebnisse der Forscher, dass sich die heutige Deep-Learning-Architektur in einem Zustand der „Überparametrisierung“ und „Unterabtastung“ befindet Die Leistung ist ähnlich (wobei das Modell über viele Generationen hinweg auf begrenzten Daten trainiert wird, bis es überpasst: die oben abgebildete „reale Welt“) und auch im Fall „unterparametrisiert“ vs. „online“ (wo das Modell nur für eine Generation trainiert). , und jede Probe wird nur einmal gesehen: das ist die „ideale Welt“ im Bild oben) Es besteht kein Zweifel, dass statistisches Lernen eine wichtige Rolle beim Deep Learning spielt. Wenn Sie sich Deep Learning jedoch einfach als ein Modell vorstellen, das mehr Knöpfe als ein klassisches Modell hat, übersehen Sie viele der Erfolgsfaktoren. Noch unpassender ist die sogenannte Metapher vom „menschlichen Studenten“. Deep Learning ähnelt der biologischen Evolution darin, dass es zwar viele wiederholte Anwendungen derselben Regel (d. h. Gradientenabstieg mit Erfahrungsverlust) liefert, aber hochkomplexe Ergebnisse liefert. Verschiedene Komponenten eines neuronalen Netzwerks scheinen zu unterschiedlichen Zeiten unterschiedliche Dinge zu lernen, darunter Repräsentationslernen, prädiktive Anpassung, implizite Regularisierung und reines Rauschen. Wir sind immer noch auf der Suche nach der richtigen Linse, um Fragen zum Thema Deep Learning zu stellen, geschweige denn zu beantworten. Der Weg ist noch lang und wir werden Sie gemeinsam ermutigen.  Starke Abhängigkeit von Verlust und Daten. Bei der Anpassung eines Modells an hochdimensionale Daten kann ein kleines Detail einen großen Unterschied in den Ergebnissen bewirken. Statistiker wissen, dass Entscheidungen wie L1- oder L2-Regularisierer wichtig sind, ganz zu schweigen davon, dass bei Verwendung völlig unterschiedlicher Datensätze eine unterschiedliche Anzahl hochdimensionaler Optimierer extrem unterschiedlich sein wird.
Starke Abhängigkeit von Verlust und Daten. Bei der Anpassung eines Modells an hochdimensionale Daten kann ein kleines Detail einen großen Unterschied in den Ergebnissen bewirken. Statistiker wissen, dass Entscheidungen wie L1- oder L2-Regularisierer wichtig sind, ganz zu schweigen davon, dass bei Verwendung völlig unterschiedlicher Datensätze eine unterschiedliche Anzahl hochdimensionaler Optimierer extrem unterschiedlich sein wird. 
Szenario B: Mathematik lernen
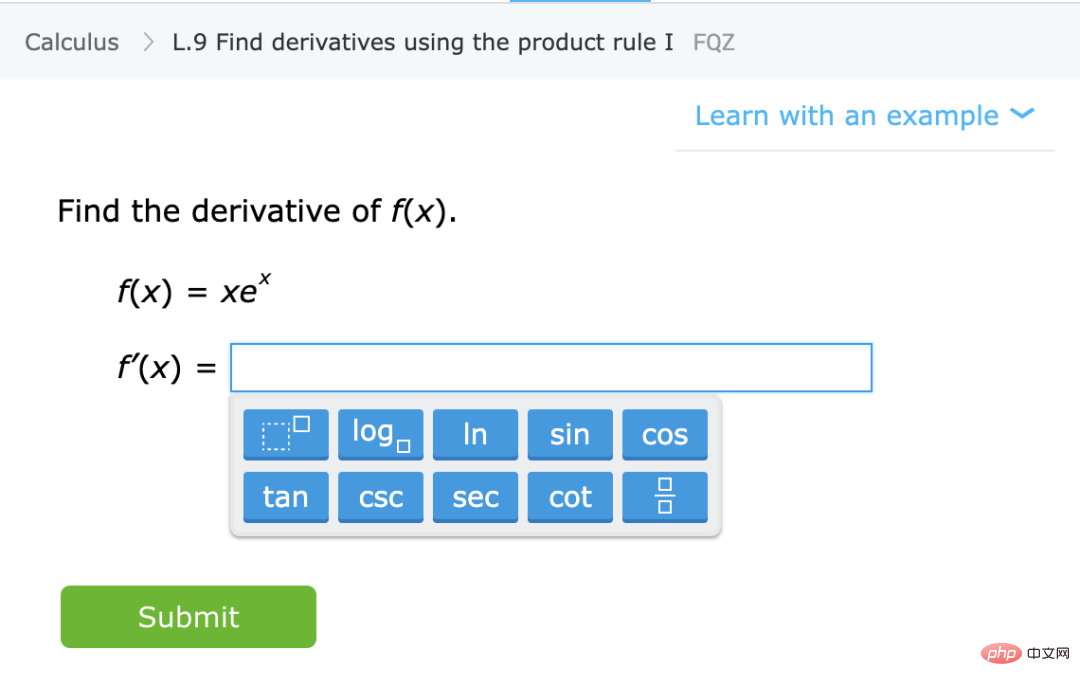 #🎜🎜 #
#🎜🎜 #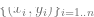 , wobei
, wobei 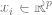 ein bestimmter Datenpunkt ist (z als spezifisches Bild),
ein bestimmter Datenpunkt ist (z als spezifisches Bild), 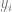 ist ein Tag.
ist ein Tag. 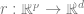 #🎜 🎜#
#🎜 🎜#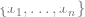 Ohne Verwendung von Etiketten, durch Minimierung einer Art selbstüberwachter Verlustfunktion. Beispiele für solche Verlustfunktionen sind Rekonstruktion oder Bild-in-Bild (Wiederherstellung eines Teils einer anderen Eingabe x) oder kontrastives Lernen (das Finden von ist deutlich kleiner, wenn
Ohne Verwendung von Etiketten, durch Minimierung einer Art selbstüberwachter Verlustfunktion. Beispiele für solche Verlustfunktionen sind Rekonstruktion oder Bild-in-Bild (Wiederherstellung eines Teils einer anderen Eingabe x) oder kontrastives Lernen (das Finden von ist deutlich kleiner, wenn 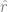 das ist Inkrement des gleichen Datenpunkts, die Parallelbeziehung ist viel kleiner als die Parallelbeziehung zwischen zwei Zufallspunkten).
das ist Inkrement des gleichen Datenpunkts, die Parallelbeziehung ist viel kleiner als die Parallelbeziehung zwischen zwei Zufallspunkten). 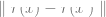 3 Dann verwenden wir die vollständig beschrifteten Daten
3 Dann verwenden wir die vollständig beschrifteten Daten 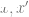 , um den linearen Klassifikator
, um den linearen Klassifikator 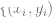 . Schritt 3 ist nur für lineare Klassifikatoren geeignet, daher geschieht die „Magie“ in Schritt 2 (selbstüberwachtes Lernen tiefer Netzwerke). Beim selbstüberwachten Lernen können unter anderem folgende Eigenschaften beobachtet werden:
. Schritt 3 ist nur für lineare Klassifikatoren geeignet, daher geschieht die „Magie“ in Schritt 2 (selbstüberwachtes Lernen tiefer Netzwerke). Beim selbstüberwachten Lernen können unter anderem folgende Eigenschaften beobachtet werden: 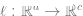
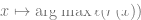 Erlernen einer Fertigkeit statt Annäherung an eine Funktion. Beim selbstüberwachten Lernen geht es nicht um die Approximation einer Funktion, sondern um das Erlernen von Darstellungen, die für eine Vielzahl nachgelagerter Aufgaben verwendet werden können. Unter der Annahme, dass dies das vorherrschende Paradigma in der Verarbeitung natürlicher Sprache ist, ist es zweitrangig, ob nachgelagerte Aufgaben durch lineare Sondierung, Feinabstimmung oder Eingabeaufforderung erhalten werden.
Erlernen einer Fertigkeit statt Annäherung an eine Funktion. Beim selbstüberwachten Lernen geht es nicht um die Approximation einer Funktion, sondern um das Erlernen von Darstellungen, die für eine Vielzahl nachgelagerter Aufgaben verwendet werden können. Unter der Annahme, dass dies das vorherrschende Paradigma in der Verarbeitung natürlicher Sprache ist, ist es zweitrangig, ob nachgelagerte Aufgaben durch lineare Sondierung, Feinabstimmung oder Eingabeaufforderung erhalten werden. 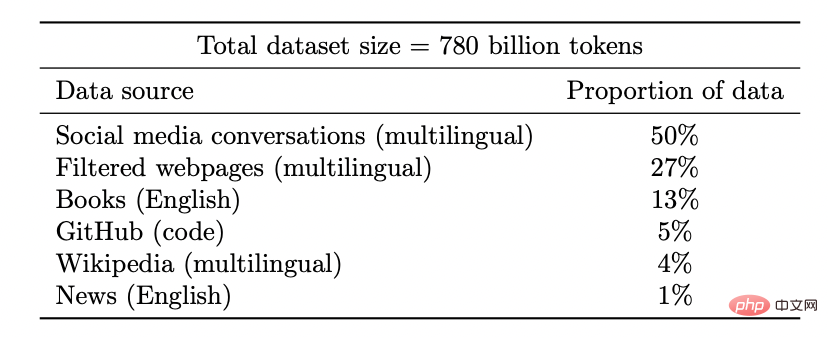
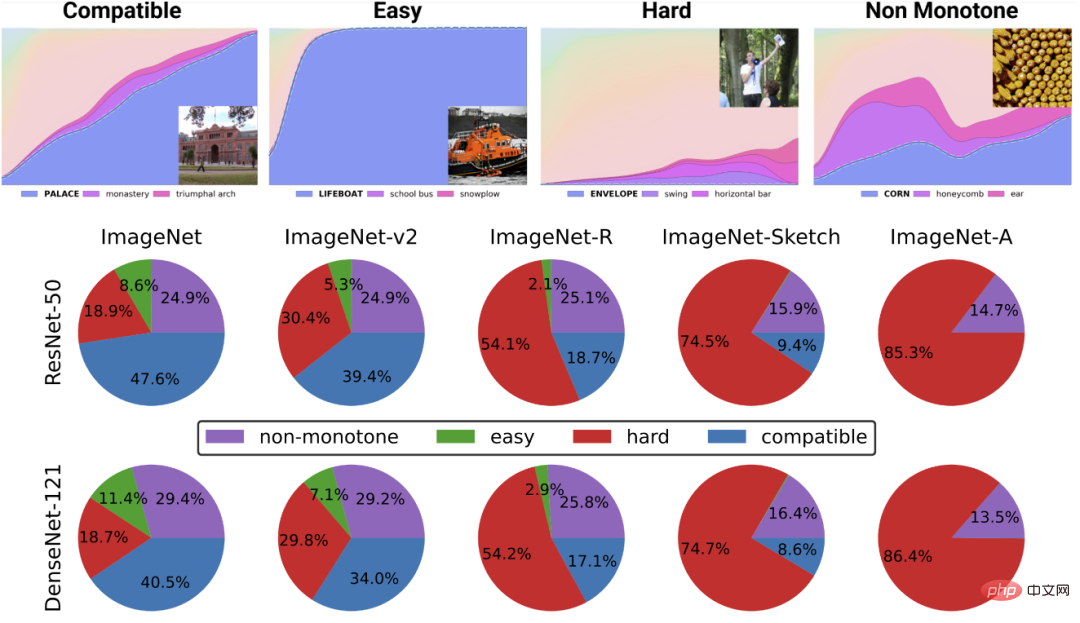
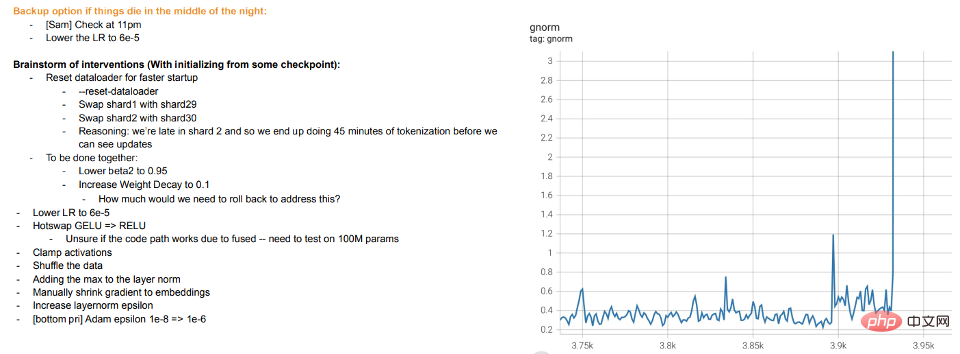

Fall 1: Überwachtes Lernen
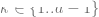 die ersten k Schichten eines mit Selbstüberwachung trainierten Deep-D-Modells mit den letzten d-k-Schichten des überwachten Modells „zusammenfügen“ und die Leistung nahezu unverändert lassen.
die ersten k Schichten eines mit Selbstüberwachung trainierten Deep-D-Modells mit den letzten d-k-Schichten des überwachten Modells „zusammenfügen“ und die Leistung nahezu unverändert lassen. 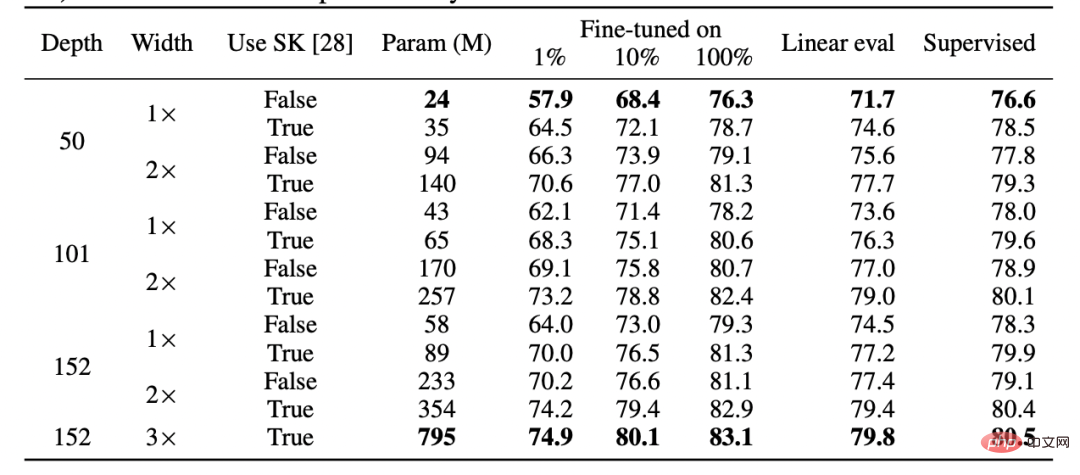
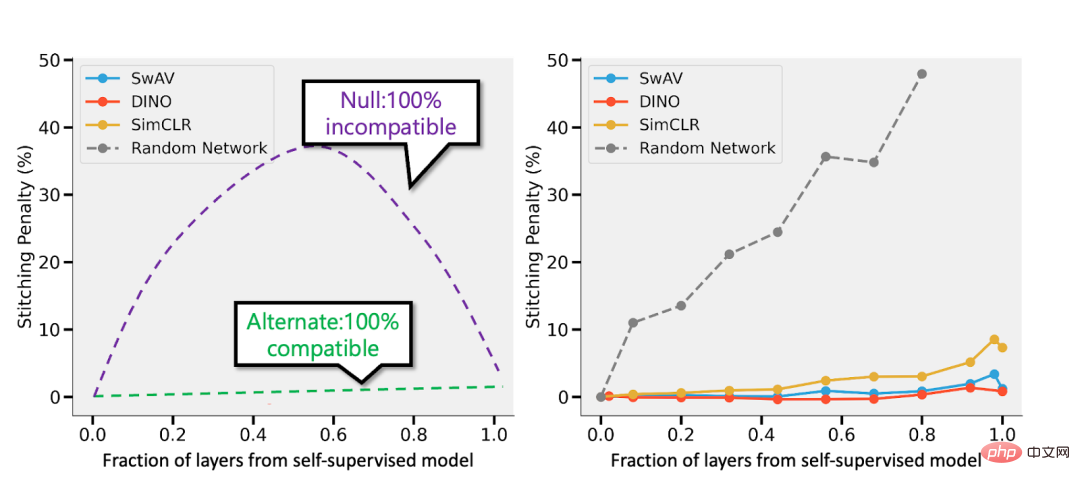
5 Zusammenfassung
Das obige ist der detaillierte Inhalt vonTheoretischer Informatiker Boaz Barak: Deep Learning ist keine „einfache Statistik', und die beiden entfernen sich immer weiter. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1376
1376
 52
52
 Methoden und Schritte zur Verwendung von BERT für die Stimmungsanalyse in Python
Jan 22, 2024 pm 04:24 PM
Methoden und Schritte zur Verwendung von BERT für die Stimmungsanalyse in Python
Jan 22, 2024 pm 04:24 PM
BERT ist ein vorab trainiertes Deep-Learning-Sprachmodell, das 2018 von Google vorgeschlagen wurde. Der vollständige Name lautet BidirektionalEncoderRepresentationsfromTransformers, der auf der Transformer-Architektur basiert und die Eigenschaften einer bidirektionalen Codierung aufweist. Im Vergleich zu herkömmlichen Einweg-Codierungsmodellen kann BERT bei der Textverarbeitung gleichzeitig Kontextinformationen berücksichtigen, sodass es bei Verarbeitungsaufgaben in natürlicher Sprache eine gute Leistung erbringt. Seine Bidirektionalität ermöglicht es BERT, die semantischen Beziehungen in Sätzen besser zu verstehen und dadurch die Ausdrucksfähigkeit des Modells zu verbessern. Durch Vorschulungs- und Feinabstimmungsmethoden kann BERT für verschiedene Aufgaben der Verarbeitung natürlicher Sprache verwendet werden, wie z. B. Stimmungsanalyse und Benennung
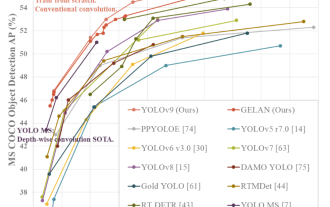 YOLO ist unsterblich! YOLOv9 wird veröffentlicht: Leistung und Geschwindigkeit SOTA~
Feb 26, 2024 am 11:31 AM
YOLO ist unsterblich! YOLOv9 wird veröffentlicht: Leistung und Geschwindigkeit SOTA~
Feb 26, 2024 am 11:31 AM
Heutige Deep-Learning-Methoden konzentrieren sich darauf, die am besten geeignete Zielfunktion zu entwerfen, damit die Vorhersageergebnisse des Modells der tatsächlichen Situation am nächsten kommen. Gleichzeitig muss eine geeignete Architektur entworfen werden, um ausreichend Informationen für die Vorhersage zu erhalten. Bestehende Methoden ignorieren die Tatsache, dass bei der schichtweisen Merkmalsextraktion und räumlichen Transformation der Eingabedaten eine große Menge an Informationen verloren geht. Dieser Artikel befasst sich mit wichtigen Themen bei der Datenübertragung über tiefe Netzwerke, nämlich Informationsengpässen und umkehrbaren Funktionen. Darauf aufbauend wird das Konzept der programmierbaren Gradienteninformation (PGI) vorgeschlagen, um die verschiedenen Änderungen zu bewältigen, die tiefe Netzwerke zur Erreichung mehrerer Ziele erfordern. PGI kann vollständige Eingabeinformationen für die Zielaufgabe zur Berechnung der Zielfunktion bereitstellen und so zuverlässige Gradienteninformationen zur Aktualisierung der Netzwerkgewichte erhalten. Darüber hinaus wird ein neues, leichtgewichtiges Netzwerk-Framework entworfen
 Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Heute diskutieren wir darüber, wie Deep-Learning-Technologie die Leistung von visionbasiertem SLAM (Simultaneous Localization and Mapping) in komplexen Umgebungen verbessern kann. Durch die Kombination von Methoden zur Tiefenmerkmalsextraktion und Tiefenanpassung stellen wir hier ein vielseitiges hybrides visuelles SLAM-System vor, das die Anpassung in anspruchsvollen Szenarien wie schlechten Lichtverhältnissen, dynamischer Beleuchtung, schwach strukturierten Bereichen und starkem Jitter verbessern soll. Unser System unterstützt mehrere Modi, einschließlich erweiterter Monokular-, Stereo-, Monokular-Trägheits- und Stereo-Trägheitskonfigurationen. Darüber hinaus wird analysiert, wie visuelles SLAM mit Deep-Learning-Methoden kombiniert werden kann, um andere Forschungen zu inspirieren. Durch umfangreiche Experimente mit öffentlichen Datensätzen und selbst abgetasteten Daten demonstrieren wir die Überlegenheit von SL-SLAM in Bezug auf Positionierungsgenauigkeit und Tracking-Robustheit.
 Latente Raumeinbettung: Erklärung und Demonstration
Jan 22, 2024 pm 05:30 PM
Latente Raumeinbettung: Erklärung und Demonstration
Jan 22, 2024 pm 05:30 PM
Latent Space Embedding (LatentSpaceEmbedding) ist der Prozess der Abbildung hochdimensionaler Daten auf niedrigdimensionalen Raum. Im Bereich des maschinellen Lernens und des tiefen Lernens handelt es sich bei der Einbettung latenter Räume normalerweise um ein neuronales Netzwerkmodell, das hochdimensionale Eingabedaten in einen Satz niedrigdimensionaler Vektordarstellungen abbildet. Dieser Satz von Vektoren wird oft als „latente Vektoren“ oder „latent“ bezeichnet Kodierungen". Der Zweck der Einbettung latenter Räume besteht darin, wichtige Merkmale in den Daten zu erfassen und sie in einer prägnanteren und verständlicheren Form darzustellen. Durch die Einbettung latenter Räume können wir Vorgänge wie das Visualisieren, Klassifizieren und Clustern von Daten im niedrigdimensionalen Raum durchführen, um die Daten besser zu verstehen und zu nutzen. Die Einbettung latenter Räume findet in vielen Bereichen breite Anwendung, z. B. bei der Bilderzeugung, der Merkmalsextraktion, der Dimensionsreduzierung usw. Die Einbettung des latenten Raums ist das Wichtigste
 Verstehen Sie in einem Artikel: die Zusammenhänge und Unterschiede zwischen KI, maschinellem Lernen und Deep Learning
Mar 02, 2024 am 11:19 AM
Verstehen Sie in einem Artikel: die Zusammenhänge und Unterschiede zwischen KI, maschinellem Lernen und Deep Learning
Mar 02, 2024 am 11:19 AM
In der heutigen Welle rasanter technologischer Veränderungen sind künstliche Intelligenz (KI), maschinelles Lernen (ML) und Deep Learning (DL) wie helle Sterne und führen die neue Welle der Informationstechnologie an. Diese drei Wörter tauchen häufig in verschiedenen hochaktuellen Diskussionen und praktischen Anwendungen auf, aber für viele Entdecker, die neu auf diesem Gebiet sind, sind ihre spezifische Bedeutung und ihre internen Zusammenhänge möglicherweise noch immer rätselhaft. Schauen wir uns also zunächst dieses Bild an. Es ist ersichtlich, dass zwischen Deep Learning, maschinellem Lernen und künstlicher Intelligenz ein enger Zusammenhang und eine fortschreitende Beziehung besteht. Deep Learning ist ein spezifischer Bereich des maschinellen Lernens und des maschinellen Lernens
 Super stark! Top 10 Deep-Learning-Algorithmen!
Mar 15, 2024 pm 03:46 PM
Super stark! Top 10 Deep-Learning-Algorithmen!
Mar 15, 2024 pm 03:46 PM
Fast 20 Jahre sind vergangen, seit das Konzept des Deep Learning im Jahr 2006 vorgeschlagen wurde. Deep Learning hat als Revolution auf dem Gebiet der künstlichen Intelligenz viele einflussreiche Algorithmen hervorgebracht. Was sind Ihrer Meinung nach die zehn besten Algorithmen für Deep Learning? Im Folgenden sind meiner Meinung nach die besten Algorithmen für Deep Learning aufgeführt. Sie alle nehmen hinsichtlich Innovation, Anwendungswert und Einfluss eine wichtige Position ein. 1. Hintergrund des Deep Neural Network (DNN): Deep Neural Network (DNN), auch Multi-Layer-Perceptron genannt, ist der am weitesten verbreitete Deep-Learning-Algorithmus. Als er erstmals erfunden wurde, wurde er aufgrund des Engpasses bei der Rechenleistung in Frage gestellt Jahre, Rechenleistung, Der Durchbruch kam mit der Datenexplosion. DNN ist ein neuronales Netzwerkmodell, das mehrere verborgene Schichten enthält. In diesem Modell übergibt jede Schicht Eingaben an die nächste Schicht und
 1,3 ms dauert 1,3 ms! Tsinghuas neueste Open-Source-Architektur für mobile neuronale Netzwerke RepViT
Mar 11, 2024 pm 12:07 PM
1,3 ms dauert 1,3 ms! Tsinghuas neueste Open-Source-Architektur für mobile neuronale Netzwerke RepViT
Mar 11, 2024 pm 12:07 PM
Papieradresse: https://arxiv.org/abs/2307.09283 Codeadresse: https://github.com/THU-MIG/RepViTRepViT funktioniert gut in der mobilen ViT-Architektur und zeigt erhebliche Vorteile. Als nächstes untersuchen wir die Beiträge dieser Studie. In dem Artikel wird erwähnt, dass Lightweight-ViTs bei visuellen Aufgaben im Allgemeinen eine bessere Leistung erbringen als Lightweight-CNNs, hauptsächlich aufgrund ihres Multi-Head-Selbstaufmerksamkeitsmoduls (MSHA), das es dem Modell ermöglicht, globale Darstellungen zu lernen. Allerdings wurden die architektonischen Unterschiede zwischen Lightweight-ViTs und Lightweight-CNNs noch nicht vollständig untersucht. In dieser Studie integrierten die Autoren leichte ViTs in die effektiven
 So verwenden Sie CNN- und Transformer-Hybridmodelle, um die Leistung zu verbessern
Jan 24, 2024 am 10:33 AM
So verwenden Sie CNN- und Transformer-Hybridmodelle, um die Leistung zu verbessern
Jan 24, 2024 am 10:33 AM
Convolutional Neural Network (CNN) und Transformer sind zwei verschiedene Deep-Learning-Modelle, die bei verschiedenen Aufgaben eine hervorragende Leistung gezeigt haben. CNN wird hauptsächlich für Computer-Vision-Aufgaben wie Bildklassifizierung, Zielerkennung und Bildsegmentierung verwendet. Es extrahiert lokale Merkmale auf dem Bild durch Faltungsoperationen und führt eine Reduzierung der Merkmalsdimensionalität und räumliche Invarianz durch Pooling-Operationen durch. Im Gegensatz dazu wird Transformer hauptsächlich für Aufgaben der Verarbeitung natürlicher Sprache (NLP) wie maschinelle Übersetzung, Textklassifizierung und Spracherkennung verwendet. Es nutzt einen Selbstaufmerksamkeitsmechanismus, um Abhängigkeiten in Sequenzen zu modellieren und vermeidet so die sequentielle Berechnung in herkömmlichen rekurrenten neuronalen Netzen. Obwohl diese beiden Modelle für unterschiedliche Aufgaben verwendet werden, weisen sie Ähnlichkeiten in der Sequenzmodellierung auf



