

Teil 01
●Was ist Bilderinbettung? ●
Graph-Einbettung ist die Abbildung der Graphstruktur Daten Es handelt sich um einen Prozess niederdimensionaler dichter Vektoren, und gleichzeitig liegen die Knoten mit ähnlichen topologischen Strukturen oder ähnlichen Attributen im ursprünglichen Diagramm auch nahe beieinander im Vektorraum, was das Problem gut lösen kann, dass Diagramm- Es ist schwierig, strukturierte Daten effizient in Algorithmen für maschinelles Lernen einzugeben.
Für die Darstellung und Speicherung von Diagrammen ist die Verwendung der Adjazenzmatrix am einfachsten. Nummerieren Sie jeden Knoten im Diagramm, um eine Matrix von  zu erstellen, wobei
zu erstellen, wobei 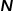 die Anzahl der Knoten im Diagramm darstellt. Ob zwei beliebige Knoten im Diagramm durch eine Kante verbunden sind, bestimmt den Wert der entsprechenden Position in der Adjazenzmatrix. Diese Darstellungsmethode ist sehr einfach zu verstehen und intuitiv, aber sehr ineffizient. Da Diagramme in realen Szenarien Tausende oder sogar mehr Knoten enthalten können und die meisten Knoten nicht durch Kanten verbunden sind, führt dies dazu, dass die resultierende Adjazenzmatrix sehr dünn ist. Die Verwendung von Adjazenzmatrizen zur Darstellung und Speicherung von Diagrammen erfordert hohe Rechen- und Platzkosten, während Diagrammeinbettungsalgorithmen Probleme bei der Diagrammanalyse effizient lösen können.
die Anzahl der Knoten im Diagramm darstellt. Ob zwei beliebige Knoten im Diagramm durch eine Kante verbunden sind, bestimmt den Wert der entsprechenden Position in der Adjazenzmatrix. Diese Darstellungsmethode ist sehr einfach zu verstehen und intuitiv, aber sehr ineffizient. Da Diagramme in realen Szenarien Tausende oder sogar mehr Knoten enthalten können und die meisten Knoten nicht durch Kanten verbunden sind, führt dies dazu, dass die resultierende Adjazenzmatrix sehr dünn ist. Die Verwendung von Adjazenzmatrizen zur Darstellung und Speicherung von Diagrammen erfordert hohe Rechen- und Platzkosten, während Diagrammeinbettungsalgorithmen Probleme bei der Diagrammanalyse effizient lösen können.
Teil 02
● Grundkonzept ●
Konzept 1 Bild:
Der-Graph wird als 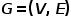 dargestellt, wobei
dargestellt, wobei 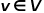 Knoten und
Knoten und 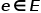 Kanten darstellt.
Kanten darstellt. 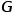 ist mit der Knotentyp-Zuordnungsfunktion
ist mit der Knotentyp-Zuordnungsfunktion 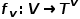 und der Kantentyp-Zuordnungsfunktion
und der Kantentyp-Zuordnungsfunktion 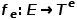 verbunden.
verbunden. 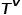 stellt die Menge der Knotentypen dar und
stellt die Menge der Knotentypen dar und 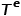 stellt die Menge der Kantentypen dar.
stellt die Menge der Kantentypen dar.
Konzept 2 Isomorpher Graph:
Graph 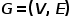 , wobei
, wobei 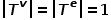 . Das heißt, alle Knoten gehören zu einem Typ und alle Kanten gehören zu einem Typ. Beispielsweise hat das Benutzeraufmerksamkeitsbeziehungsdiagramm in einem sozialen Netzwerk nur einen Knotentyp (Benutzer) und einen Kantentyp (Aufmerksamkeitsbeziehung).
. Das heißt, alle Knoten gehören zu einem Typ und alle Kanten gehören zu einem Typ. Beispielsweise hat das Benutzeraufmerksamkeitsbeziehungsdiagramm in einem sozialen Netzwerk nur einen Knotentyp (Benutzer) und einen Kantentyp (Aufmerksamkeitsbeziehung).
Konzept 3 Heterogener Graph:
Graph 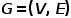 , wobei
, wobei 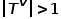 oder.
oder. 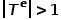 . Das heißt, es gibt mehr als einen Knotentyp oder Kantentyp. Beispielsweise gibt es in der Diagrammstruktur in einem akademischen Netzwerk mehrere Knotentypen wie Aufsätze, Autoren, Konferenzen usw. Die Kantenbeziehungen umfassen die kreative Beziehung zwischen Autoren und Aufsätzen, Aufsätzen und Konferenzen, der Publikationsbeziehung zwischen ihnen, der Zitierbeziehung zwischen Aufsätzen usw.
. Das heißt, es gibt mehr als einen Knotentyp oder Kantentyp. Beispielsweise gibt es in der Diagrammstruktur in einem akademischen Netzwerk mehrere Knotentypen wie Aufsätze, Autoren, Konferenzen usw. Die Kantenbeziehungen umfassen die kreative Beziehung zwischen Autoren und Aufsätzen, Aufsätzen und Konferenzen, der Publikationsbeziehung zwischen ihnen, der Zitierbeziehung zwischen Aufsätzen usw.
Konzept 4 Ähnlichkeit erster Ordnung:
Wenn das Gewicht der Kante, die zwei Knoten verbindet, größer ist, ist die Ähnlichkeit erster Ordnung zwischen ihnen größer. Die Ähnlichkeit erster Ordnung zwischen Knoten 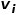 und Knoten
und Knoten 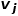 ausgedrückt als
ausgedrückt als 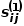 , es gibt
, es gibt 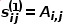 , darunter #🎜🎜 #
, darunter #🎜🎜 # 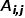 ist Knoten
ist Knoten 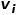 und Knoten # 🎜 Das Gewicht der Kante
und Knoten # 🎜 Das Gewicht der Kante 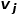 zwischen 🎜#
zwischen 🎜# .
.
Konzept 5 Ähnlichkeit zweiter Ordnung: #🎜🎜 #
Wenn die Netzwerkstrukturen zweier benachbarter Knoten ähnlicher sind, ist die Ähnlichkeit zweiter Ordnung zwischen ihnen umso größer. Ähnlichkeit zweiter Ordnung zwischen Knoten und Knoten 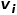 #🎜 🎜#
#🎜 🎜#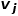 ist die Nachbarschaft von
ist die Nachbarschaft von 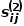 Die Nachbarschaft von 🎜##🎜🎜 #
Die Nachbarschaft von 🎜##🎜🎜 #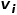 und
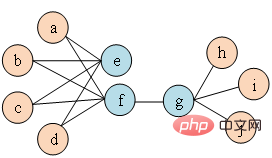
und 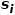 Ähnlichkeit zwischen #🎜 🎜#. Wie in Abbildung 1 gezeigt, sind Knoten f und Knoten g erster Ordnung ähnlich, da es eine Kante gibt, die Knoten f und Knoten g verbindet. Obwohl es keine Kante gibt, die Knoten e und Knoten g verbindet, haben sie vier identische Nachbarknoten, sodass Knoten e und Knoten g zweiter Ordnung ähnlich sind.
Ähnlichkeit zwischen #🎜 🎜#. Wie in Abbildung 1 gezeigt, sind Knoten f und Knoten g erster Ordnung ähnlich, da es eine Kante gibt, die Knoten f und Knoten g verbindet. Obwohl es keine Kante gibt, die Knoten e und Knoten g verbindet, haben sie vier identische Nachbarknoten, sodass Knoten e und Knoten g zweiter Ordnung ähnlich sind. 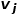
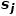
... Konvertieren Sie das Diagramm so weit wie möglich in einen dimensionalen Raum und behalten Sie dabei die Diagrammeigenschaften bei. Verlassen Sie sich auf Ähnlichkeit erster Ordnung oder Ähnlichkeit höherer Ordnung, um den Grad der Erhaltung von Diagrammeigenschaften zu quantifizieren, indem Sie einen Dimensionsvektor oder einen Satz dimensionaler Vektoren verwenden, um einen Graphen darzustellen, wobei jeder Vektor die Einbettung eines Teils davon darstellt das Diagramm, beispielsweise ein Knoten oder eine Kante.
Teil 03
●  Klassifizierung des Grapheinbettungsalgorithmus
Klassifizierung des Grapheinbettungsalgorithmus
●
In den letzten Jahrzehnten Forscher haben viele hervorragende Algorithmen vorgeschlagen, die nachweislich erhebliche Auswirkungen auf soziale Netzwerke, Kommunikationsnetzwerke und andere Szenarien haben. Die Branche unterteilt diese Grapheinbettungsalgorithmen normalerweise in die folgenden drei Kategorien, basierend auf Unterschieden in der Ausgabegranularität: (1) Knoteneinbettung Knoteneinbettung ist der häufigste Typ, bei dem Vektoren in niedriger Auflösung verwendet werden. Dimensionsraum Da er jeden Knoten im Diagramm darstellt, sind auch die Einbettungsvektordarstellungen „ähnlicher“ Knoten ähnlich. Wenn es notwendig ist, die Knoten im Diagramm zu analysieren und dann Aufgaben wie Knotenklassifizierung oder Knotenclusterung durchzuführen, wird normalerweise die Knoteneinbettung gewählt.
(2) Kanteneinbettung
verwendet einen Vektor, um jede Kante im Diagramm in einem niedrigdimensionalen Raum darzustellen. Eine Kante besteht aus einem Knotenpaar und stellt normalerweise eine Knotenpaarbeziehung dar. Die Kanteneinbettung eignet sich, wenn Sie die Kanten im Diagramm analysieren und Aufgaben wie die Vorhersage von Wissensdiagrammbeziehungen oder Linkvorhersagen ausführen müssen.
(3) Diagrammeinbettung
verwendet Vektoren, um das gesamte Diagramm in einem niedrigdimensionalen Raum darzustellen, normalerweise ein kleines Diagramm wie ein Molekül oder Protein. Die Darstellung eines Graphen als Vektor erleichtert die Berechnung von Ähnlichkeiten zwischen verschiedenen Graphen und löst so Probleme bei der Graphklassifizierung.
Unterschiedliche Aufgabenanforderungen bestimmen den ausgewählten Grapheneinbettungsalgorithmus. Aus Platzgründen werden hier der DeepWalk-Algorithmus und der Node2Vec-Algorithmus für die Knoteneinbettung zum relativ detaillierten Lernen ausgewählt.
Teil 04
●
●
1.DeepWalk-Algorithmus Inspiriert von der Idee von word2vec im Bereich Zur Verarbeitung natürlicher Sprache schlugen Perozzi et al. DeepWalk vor, um ein Modell zum Lernen von Knotendarstellungsvektoren im Diagramm zu erstellen und die Kookkurrenzbeziehung zwischen Knoten mit der Kookkurrenzbeziehung zwischen Wörtern im Korpus zu vergleichen. Die Nachbarknotensequenz der Knoten im Diagramm wird durch zufällige Spaziergänge gesammelt, was einem Korpus von Knotenkontexten entspricht, und kann somit das Problem der Extraktion von Kookkurrenzbeziehungen zwischen Knoten im Diagramm lösen. Legen Sie die Länge und den Startpunkt der Knotensequenz im Voraus fest. Die Random-Walk-Strategie dient zur Bestimmung des nächsten Walking-Knotens unter den Nachbarknoten. Wiederholen Sie diesen Schritt, um eine Sequenz zu erhalten, die die Bedingungen erfüllt 2. Zeigen.
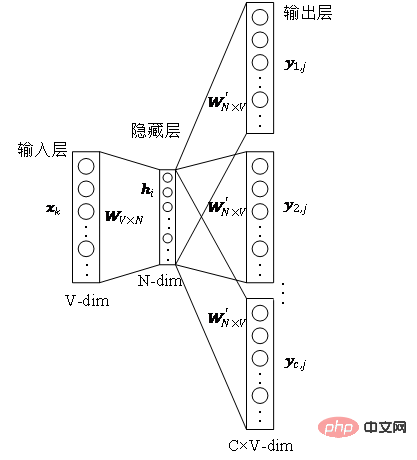
Abbildung 2 Zufallsgangdiagramm # 🎜🎜# Entspricht den Wörtern im Word2vec-Algorithmus den Knoten im Diagramm Um die latente Merkmalsdarstellung von Knoten weiter zu lernen, wird der DeepWalk Der Algorithmus führt die Mapping-Funktion ein # dimensionale Vektorabbildung, dann wird das Problem in die Abschätzung der Möglichkeit der folgenden Formel umgewandelt. Wie in Abbildung 3 gezeigt, enthält das Skip-Gramm-Modell zwei Schlüsselmatrizen, eine davon ist die zentrale Wortvektormatrix#🎜🎜 # , das andere ist die Hintergrundwortvektormatrix , diese beiden Gewichte Die Matrizen stellen jeweils die Wortvektoren dar, die Wörtern in unterschiedlichen Rollen zugeordnet sind. Skip-Gram ist ein Modell zur Vorhersage des Wortkontexts. Es lernt zunächst die Beziehungen zwischen Wörtern aus dem Korpus und verwendet diese Beziehungen dann, um den Kontext eines bestimmten Wortes auszudrücken, dh die Vektordarstellung des Wortes. Das heißt, je häufiger in derselben Reihenfolge zwei Wörter gleichzeitig vorkommen, desto ähnlicher sind die Vektordarstellungen der beiden Wörter. Wenden Sie diese Idee auf das Diagramm an und definieren Sie seine Optimierungszielfunktion wie in der Formel gezeigt. #🎜🎜 #2.Node2Vec-Algorithmus Basierend auf dem DeepWalk-Algorithmus haben die Forscher Grover A und Leskovec J den Node2Vec-Algorithmus vorgeschlagen. Der Node2Vec-Algorithmus optimiert den Prozess der Generierung von Knotensequenzen durch Random Walks im DeepWalk-Algorithmus und definiert Parameter wobei #🎜🎜. # Die Random-Walk-Strategie von Node2Vec wird basierend auf zwei Parametern gesteuert, wie in Abbildung 4 dargestellt. Nehmen Sie an, dass der Knoten v über die Kante , Knoten (2) Wenn (3) Wenn Kontrolle Mit der Wahrscheinlichkeit, zum vorherigen Hop-Knoten zurückzukehren, steuert der Parameter #🎜 🎜 # ● Zusammenfassung #🎜 🎜# ● Mit der rasanten Entwicklung der Informationstechnologie ist die Netzwerkumgebung immer komplexer geworden und Netzwerkangriffe treten häufig auf, was ein Sicherheitsproblem darstellt, auf das Unternehmen achten müssen. Tatsächlich ist das Netzwerk, die grundlegende Umgebung, in der APT-Angriffe stattfinden, selbst eine Netzwerkstruktur, die aus Computern und anderen Elementen besteht. Es ist nicht schwer, sich vorzustellen, Diagrammdatenstrukturen zu verwenden, um die Beziehung zwischen diesen Elementen auszudrücken und sie dann zu transformieren Angriffserkennungsproblem in Knoten-, Kanten- oder Subgraph-Klassifizierungsaufgabe in einem Diagramm. Die Einbettung von Graphen ist ein umfangreiches Thema mit großem Forschungsraum. Wie die Effizienz des Modelltrainings verbessert und die Idee der Grapheneinbettung auf weitere Produktionspraktiken angewendet werden kann, ist eine bessere Lösung erforderlich. References [1] Xu M. Verständnis für die Einbettungsmethoden und ihre Anwendungen [j]. [2]Cai H, Zheng V W, Chang K C C. Eine umfassende Übersicht über die Einbettung von Graphen: Probleme, Techniken und Anwendungen[J]. [3]Goyal P, Ferrara E. Graph-Einbettungstechniken, Anwendungen und Leistung: Eine Umfrage[J].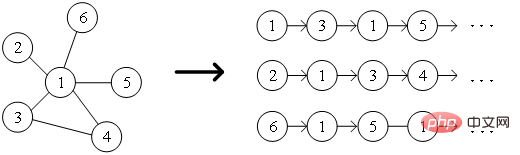
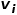 , und die Wortfolge entspricht der durch Zufallswanderung erhaltenen Knotenfolge , dann definieren Sie für einen Random Walk
, und die Wortfolge entspricht der durch Zufallswanderung erhaltenen Knotenfolge , dann definieren Sie für einen Random Walk 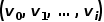 seine Optimierungszielfunktion wie in der Formel gezeigt.
seine Optimierungszielfunktion wie in der Formel gezeigt. 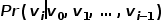
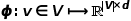
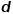 Die Berechnung der Wahrscheinlichkeit muss sich auch auf das Skip-Gramm-Modell beziehen im word2vec-Algorithmus.
Die Berechnung der Wahrscheinlichkeit muss sich auch auf das Skip-Gramm-Modell beziehen im word2vec-Algorithmus. 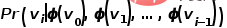
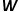 Im Random-Walk-Prozess die Beziehung zwischen den Knoten in der Stichprobe Sequenz und sequentielle Beziehung von Knoten können die Nähebeziehung von Knoten besser widerspiegeln und den Rechenaufwand reduzieren.
Im Random-Walk-Prozess die Beziehung zwischen den Knoten in der Stichprobe Sequenz und sequentielle Beziehung von Knoten können die Nähebeziehung von Knoten besser widerspiegeln und den Rechenaufwand reduzieren. 
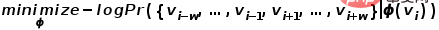
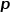 und Parameter
und Parameter 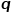 Gibt an, ob jeder Zufallsgang dazu tendiert, die Breiten-zuerst-Stichprobe oder die Tiefen-zuerst-Stichprobe zu bevorzugen, und ist daher sehr anpassungsfähig. Angenommen, der aktuelle Zugangsknoten ist
Gibt an, ob jeder Zufallsgang dazu tendiert, die Breiten-zuerst-Stichprobe oder die Tiefen-zuerst-Stichprobe zu bevorzugen, und ist daher sehr anpassungsfähig. Angenommen, der aktuelle Zugangsknoten ist 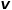 , dann ist der nächste Zugangsknoten
, dann ist der nächste Zugangsknoten 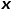 Die Wahrscheinlichkeit von wird in der Formel angezeigt.
Die Wahrscheinlichkeit von wird in der Formel angezeigt. 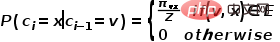
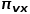 den Slave-Knoten darstellt # Die Übergangswahrscheinlichkeit von 🎜🎜#
den Slave-Knoten darstellt # Die Übergangswahrscheinlichkeit von 🎜🎜#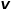 zum Knoten
zum Knoten 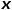 , # 🎜🎜#
, # 🎜🎜#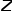 stellt die Normalisierungskonstante dar.
stellt die Normalisierungskonstante dar. 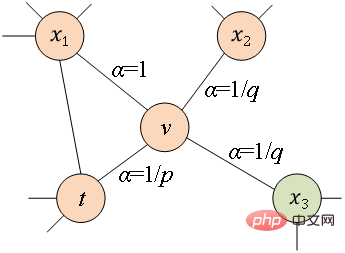
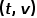 erreicht wird und der nächste Schritt darin besteht, den rechten Knoten zu besuchen. Mit anderen Worten: Wenn es sich bei dem Diagramm um ein ungewichtetes Diagramm handelt, bestimmt
erreicht wird und der nächste Schritt darin besteht, den rechten Knoten zu besuchen. Mit anderen Worten: Wenn es sich bei dem Diagramm um ein ungewichtetes Diagramm handelt, bestimmt 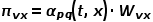 direkt die Übergangswahrscheinlichkeit des Knotens. Wenn der Graph ein gewichteter Graph ist, bestimmt das Produkt aus
direkt die Übergangswahrscheinlichkeit des Knotens. Wenn der Graph ein gewichteter Graph ist, bestimmt das Produkt aus 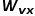 und dem Kantengewicht
und dem Kantengewicht 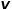 die endgültige Übergangswahrscheinlichkeit des Knotens.
die endgültige Übergangswahrscheinlichkeit des Knotens. 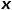 kann nach der folgenden Formel berechnet werden, wobei
kann nach der folgenden Formel berechnet werden, wobei 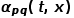 die kürzeste Pfadentfernung zwischen Knoten
die kürzeste Pfadentfernung zwischen Knoten 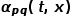 und Knoten
und Knoten 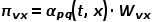 ist.
ist. 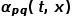 Wenn die Wanderprobe vom Knoten
Wenn die Wanderprobe vom Knoten 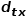 zum Knoten
zum Knoten 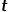 geht und den nächsten Hop-Knoten auswählen muss, treten die folgenden drei Situationen auf.
geht und den nächsten Hop-Knoten auswählen muss, treten die folgenden drei Situationen auf. 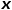 (1) Wenn
(1) Wenn 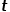 zurückgeben.
zurückgeben. 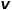
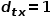 , wählen Sie den Knoten #🎜 Allgemein aus Benachbarte Knoten von 🎜#
, wählen Sie den Knoten #🎜 Allgemein aus Benachbarte Knoten von 🎜#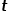 und Knoten
und Knoten 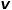 , zum Beispiel Knoten #🎜 🎜 #
, zum Beispiel Knoten #🎜 🎜 #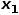 .
. 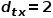 , wählen Sie die angrenzenden Knoten des Knotens
, wählen Sie die angrenzenden Knoten des Knotens 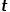 , die nichts mit dem Knoten zu tun haben, zum Beispiel: Knoten
, die nichts mit dem Knoten zu tun haben, zum Beispiel: Knoten 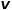 oder
oder 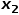 .
. 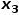
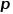 mehr, ob die lokalen Strukturinformationen oder die globalen Strukturinformationen des untersucht werden sollen Tatsächlich ist das DeepWalk-Modell das Node2Vec, wenn der Wert von
mehr, ob die lokalen Strukturinformationen oder die globalen Strukturinformationen des untersucht werden sollen Tatsächlich ist das DeepWalk-Modell das Node2Vec, wenn der Wert von 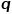 und
und 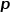 #🎜 🎜# ist auf 1 Modell eingestellt.
#🎜 🎜# ist auf 1 Modell eingestellt.  Teil 05
Teil 05
Das obige ist der detaillierte Inhalt vonEine kurze Diskussion über Algorithmen zur Grapheneinbettung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




