 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Detaillierter Vergleich der generativen Modelle VAE, GAN und flussbasierter Modelle
Detaillierter Vergleich der generativen Modelle VAE, GAN und flussbasierter Modelle
Detaillierter Vergleich der generativen Modelle VAE, GAN und flussbasierter Modelle
Zwei Jahre nachdem Ian Goodfellow und andere Forscher in einem Artikel generative gegnerische Netzwerke vorgestellt hatten, bezeichnete Yann LeCun das gegnerische Training als „die interessanteste Idee in ML im letzten Jahrzehnt“. Obwohl GANs interessant und vielversprechend sind, sind sie nur ein Teil einer Familie generativer Modelle, die traditionelle KI-Probleme aus einer völlig anderen Perspektive lösen. In diesem Artikel werden wir drei gängige generative Modelle vergleichen.
Generierungsalgorithmus
Wenn wir an maschinelles Lernen denken, fällt uns wahrscheinlich als Erstes der Diskriminanzalgorithmus ein. Unter diskriminierenden Modellen versteht man die Vorhersage von Bezeichnungen oder Kategorien von Eingabedaten auf der Grundlage ihrer Eigenschaften und ist das Herzstück aller Klassifizierungs- und Vorhersagelösungen. Im Gegensatz zu diesen Modellen helfen uns generative Algorithmen dabei, Geschichten über die Daten zu erzählen und mögliche Erklärungen dafür zu liefern, wie die Daten generiert wurden. Im Gegensatz zu diskriminierenden Algorithmen, die Merkmale Etiketten zuordnen, versuchen generative Modelle, Merkmale vorherzusagen, denen ein Etikett gegeben wurde.
Unterscheiden Sie die Beziehung zwischen der Bezeichnung y und dem durch das Modell definierten Merkmal x und generieren Sie das Modell, um die Frage „Wie erhalten Sie y“ zu beantworten. Das generative Modellmodell ist P (Beobachtung/Ursache) und verwendet dann den Satz von Bayes, um P (Ursache/Beobachtung) zu berechnen. Auf diese Weise können sie p(x|y), die Wahrscheinlichkeit von x bei gegebenem y oder die Wahrscheinlichkeit eines Merkmals bei gegebener Bezeichnung oder Klasse erfassen. Tatsächlich können generative Algorithmen also auch als Klassifikatoren verwendet werden, wahrscheinlich weil sie die Verteilung einzelner Klassen modellieren.
Es gibt viele generative Algorithmen, aber die beliebtesten Modelle, die in die Kategorie der tiefen generativen Modelle fallen, sind Variational Autoencoder (VAE), Gan und flussbasierte Modelle.
VAE
Ein Variational Autoencoder (VAE) ist ein generatives Modell, das „eine probabilistische Beschreibung von Beobachtungen in einem latenten Raum liefert“. Vereinfacht ausgedrückt bedeutet dies, dass VAE latente Attribute als Wahrscheinlichkeitsverteilungen speichert.
Die Idee von Variations-Autoencodern (Kingma & Welling, 2014) oder VAEs ist tief in Variations-Bayes'schen und grafischen Modellmethoden verwurzelt.
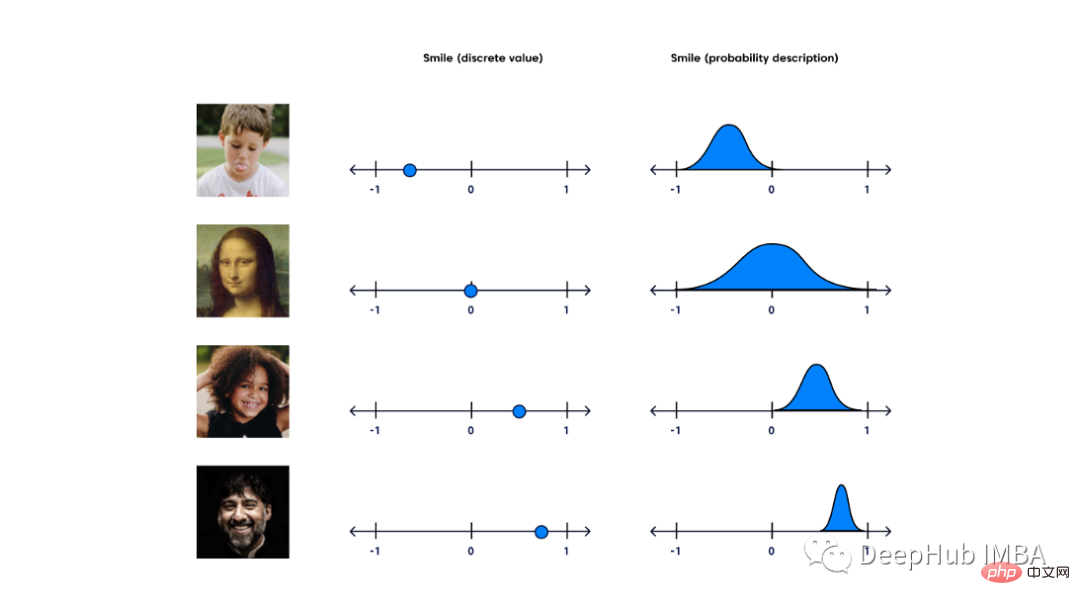
Ein Standard-Autoencoder besteht aus zwei ähnlichen Netzwerken, einem Encoder und einem Decoder. Der Encoder nimmt die Eingabe und wandelt sie in eine kleinere Darstellung um, die der Decoder verwenden kann, um sie wieder in die ursprüngliche Eingabe umzuwandeln. Der latente Raum, in den sie die Eingabe transformieren, und der Raum, in dem ihre Codierungsvektoren liegen, sind möglicherweise nicht kontinuierlich. Dies ist ein Problem für generative Modelle, da wir alle zufällig Stichproben aus einem latenten Raum entnehmen oder Variationen des Eingabebildes aus einem kontinuierlichen latenten Raum generieren möchten.
Der Variations-Autoencoder verfügt über einen kontinuierlichen latenten Raum, der die Zufallsstichprobe und Interpolation bequemer macht. Um dies zu erreichen, gibt der verborgene Knoten des Encoders nicht den Codierungsvektor aus, sondern zwei Vektoren gleicher Größe: einen Mittelwertvektor und einen Standardabweichungsvektor. Jeder verborgene Knoten betrachtet sich selbst als Gaußverteilt. Das i-te Element des Mittelwert- und Standardabweichungsvektors entspricht hier dem Mittelwert- und Standardabweichungswert der i-ten Zufallsvariablen. Wir nehmen eine Stichprobe aus diesem Verteilungsvektor und der Decoder entnimmt zufällig Stichproben aus der Wahrscheinlichkeitsverteilung des Eingabevektors. Bei diesem Prozess handelt es sich um eine Zufallsgenerierung. Das bedeutet, dass sich die tatsächliche Codierung selbst bei derselben Eingabe bei konstantem Mittelwert und Standardabweichung in jedem Durchgang unterscheidet.
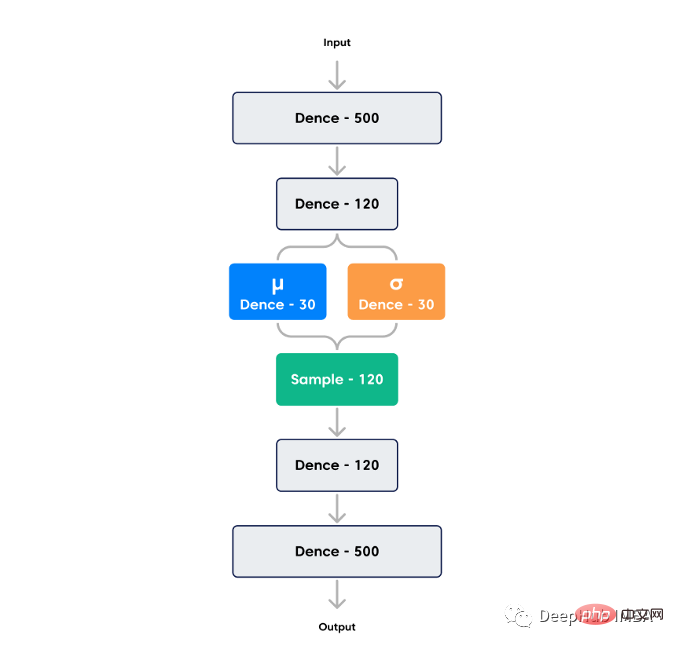
Der Verlust des Autoencoders dient dazu, den Rekonstruktionsverlust (wie ähnlich die Ausgabe der Eingabe ist) und den potenziellen Verlust (die Differenz zwischen dem) zu minimieren versteckte Knoten und die Normalverteilung) Nähe). Je kleiner der potenzielle Verlust ist, desto weniger Informationen können codiert werden, sodass der Rekonstruktionsverlust zunimmt, sodass ein Kompromiss zwischen dem potenziellen Verlust und dem Rekonstruktionsverlust besteht. Wenn der potenzielle Verlust gering ist, ist das generierte Bild dem Trainingsbild zu ähnlich, was zu einer schlechten Leistung führt. Wenn der Rekonstruktionsverlust gering ist, ist der Effekt des rekonstruierten Bildes während des Trainings besser, aber das generierte neue Bild unterscheidet sich erheblich vom rekonstruierten Bild, sodass ein gutes Gleichgewicht gefunden werden muss.
VAEs können verschiedene Arten von Daten verarbeiten, sequentiell und nicht sequentiell, kontinuierlich oder diskret, sogar beschriftet oder unbeschriftet, was sie zu sehr leistungsstarken Generierungswerkzeugen macht.
Aber ein großer Nachteil von VAEs ist die verschwommene Ausgabe, die sie erzeugen. Wie Dosovitskiy und Brox betonten, erzeugen VAE-Modelle oft unrealistische und mehrdeutige Stichproben. Dies liegt an der Art und Weise, wie die Datenverteilung wiederhergestellt und die Verlustfunktion berechnet wird. In einem Artikel von Zhao et al. aus dem Jahr 2017 wurde vorgeschlagen, VAEs ohne Verwendung von Variations-Bayes-Methoden zu modifizieren, um die Ausgabequalität zu verbessern.

Generative Adversarial Networks
Generative Adversarial Networks (GANs) sind ein generatives Modell, das auf Deep Learning basiert und neue Inhalte generieren kann . Die GAN-Architektur wurde erstmals 2014 in einem Artikel mit dem Titel „Generative Adversarial Networks“ von Ian Goodfellow et al. beschrieben.
GANs verwenden einen überwachten Lernansatz mit zwei Untermodellen: einem Generatormodell, das neue Beispiele generiert, und einem Diskriminatormodell, das versucht, Beispiele als echt oder gefälscht (generiert) zu klassifizieren.
Generator: Ein Modell zum Generieren neuer plausibler Beispiele aus der Problemdomäne.
Diskriminator: Ein Modell, das verwendet wird, um Beispiele als echt (aus der Domäne) oder gefälscht (generiert) zu klassifizieren.
Die beiden Models werden als Konkurrentinnen ausgebildet. Generatoren erzeugen Beispieldaten direkt. Sein Gegenspieler, der Diskriminator, versucht, zwischen aus den Trainingsdaten gezogenen Stichproben und aus dem Generator gezogenen Stichproben zu unterscheiden. Dieser Wettbewerbsprozess setzt sich während des Trainings fort, bis das Diskriminatormodell mehr als die Hälfte der Zeit nicht wahr oder falsch erkennen kann, was bedeutet, dass das Generatormodell sehr realistische Daten generiert.
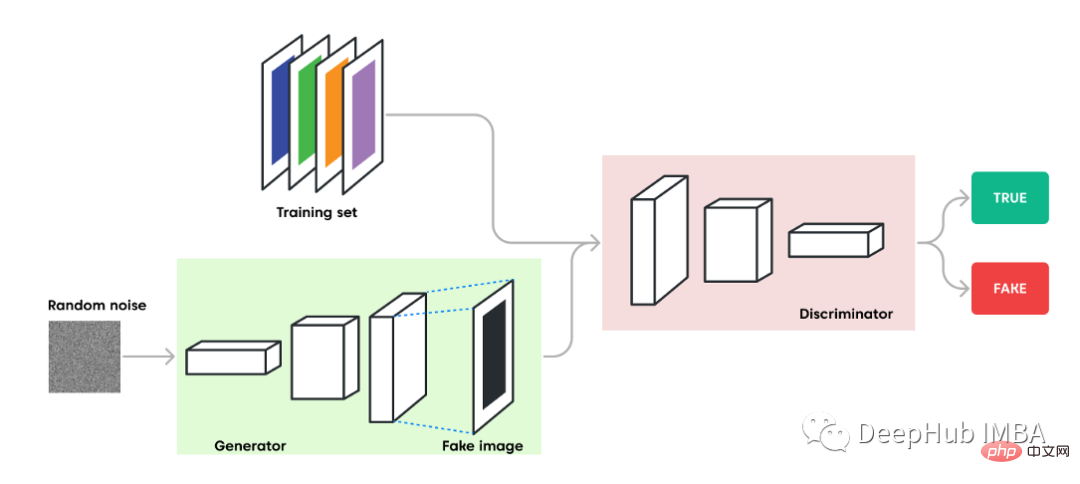
Wenn der Diskriminator erfolgreich eine echte und eine gefälschte Probe identifiziert, wird er belohnt, während seine Parameter unverändert bleiben. Wenn der Generator einen Fehler macht, wird er bestraft und seine Parameter werden aktualisiert. In einer idealen Welt kann der Generator immer dann, wenn der Diskriminator den Unterschied nicht erkennen kann und „unsicher“ vorhersagt (z. B. 50 % wahr oder falsch), eine perfekte Kopie aus der Eingabedomäne erstellen.
Aber hier kann jedes Modell das andere übertrumpfen. Wenn der Diskriminator zu gut ist, gibt er Werte zurück, die sehr nahe bei 0 oder 1 liegen, und der Generator hat Probleme, aktualisierte Farbverläufe zu erhalten. Wenn der Generator zu gut ist, nutzt er die Schwächen des Diskriminators aus und führt zu falsch negativen Ergebnissen. Daher müssen die beiden neuronalen Netze durch ihre jeweilige Lernrate ein ähnliches „Fähigkeitsniveau“ aufweisen. Dies ist auch einer der Gründe, warum GAN schwierig zu trainieren ist.
Generatormodell
Der Generator verwendet einen Zufallsvektor fester Länge als Eingabe und generiert eine Stichprobe innerhalb des definierten Bereichs. Dieser Vektor wird zufällig aus einer Gaußschen Verteilung gezogen. Nach dem Training entsprechen die Punkte in diesem mehrdimensionalen Vektorraum den Punkten in der Problemdomäne und bilden eine komprimierte Darstellung der Datenverteilung. Dieser Schritt ähnelt VAE. Dieser Vektorraum wird als latenter Raum oder Vektor bezeichnet Raum bestehend aus latenten Variablen. Der GAN-Generator mittelt ausgewählte Punkte im latenten Raum. Neue aus dem latenten Raum extrahierte Punkte können als Eingabe für das Generatormodell bereitgestellt und zur Generierung neuer und unterschiedlicher Ausgabebeispiele verwendet werden. Nach dem Training bleibt das Generatormodell erhalten und wird zum Generieren neuer Proben verwendet.
Diskriminatormodell
Das Diskriminatormodell verwendet ein Beispiel als Eingabe (entweder eine echte Stichprobe aus dem Trainingsdatensatz oder von einem Generatormodell generiert) und sagt eine binäre Klassenbezeichnung von echt oder falsch (generiert) voraus. Der Diskriminator ist ein normales (und leicht verständliches) Klassifizierungsmodell.
Nach dem Trainingsprozess wird der Diskriminator verworfen, da wir am Generator interessiert sind. Natürlich kann der Diskriminator auch für andere Zwecke verwendet werden
GANs können brauchbare Proben erzeugen, aber das ursprüngliche GAN hat auch Mängel:
- Das Bild wird durch willkürliches Rauschen erzeugt. Wenn Sie ein Bild mit bestimmten Eigenschaften erstellen, können Sie nicht sicher sein, welcher anfängliche Rauschwert dieses Bild erzeugt, sondern müssen stattdessen die gesamte Verteilung durchsuchen.
- GAN unterscheidet nur zwischen „echten“ und „gefälschten“ Bildern. Es gibt jedoch keine Einschränkung, die besagt, dass ein Foto einer „Katze“ wie eine „Katze“ aussehen muss. Daher kann es zu generierten Bildern kommen, die nicht die tatsächlichen Objekte enthalten, deren Stile jedoch ähnlich aussehen.
- GANs brauchen lange zum Trainieren. Ein GAN kann auf einer einzelnen GPU mehrere Stunden und auf einer einzelnen CPU mehr als einen Tag dauern.
Flussbasierte Modelle
Flussbasierte generative Modelle sind exakte Log-Likelihood-Modelle mit nachvollziehbarer Stichprobe und latenter Variableninferenz. Flussbasierte Modelle wenden eine Reihe reversibler Transformationen auf Stichproben aus einem früheren Zeitpunkt an, sodass die genaue Log-Likelihood einer Beobachtung berechnet werden kann. Im Gegensatz zu den beiden vorherigen Algorithmen lernt dieses Modell explizit die Datenverteilung, sodass die Verlustfunktion eine negative Log-Likelihood hat.

Bei der nichtlinearen unabhängigen Komponentenanalyse wird das Strömungsmodell f als reversible Transformation konstruiert, die eine hochdimensionale Zufallsvariable x auf eine standardmäßige Gaußsche latente Variable z=f(x) abbildet. Der Schlüsselgedanke beim Entwurf des Strömungsmodells besteht darin, dass es eine beliebige bijektive Funktion sein und durch Überlagerung einfacher reversibler Transformationen gebildet werden kann. Zusammenfassend lässt sich sagen, dass das Strömungsmodell f aus einer Reihe reversibler Strömungen wie f(x) =f1◦···◦fL(x) besteht, wobei jedes fi eine nachvollziehbare Umkehrung und eine nachvollziehbare Jacobi-Matrix aufweist.
Es gibt zwei Hauptkategorien flussbasierter Modelle: Modelle mit normalisiertem Fluss und Modelle mit autoregressivem Fluss, die versuchen, die Leistung des Basismodells zu verbessern.
Normalisiertes Strömungsmodell
Für viele Probleme des maschinellen Lernens ist die Fähigkeit, eine gute Dichteschätzung durchzuführen, von entscheidender Bedeutung. Aber es ist von Natur aus komplex: Wenn wir Backpropagation in einem Deep-Learning-Modell durchführen müssen, muss die eingebettete Wahrscheinlichkeitsverteilung einfach genug sein, damit die Ableitungen effizient berechnet werden können. Die traditionelle Lösung besteht darin, Gaußsche Verteilungen in Modellen zur Generierung latenter Variablen zu verwenden, obwohl die meisten Verteilungen in der realen Welt viel komplexer sind. Modelle mit normalisiertem Fluss (NF) wie RealNVP oder Glow bieten eine robuste Näherung der Verteilung. Sie wandeln eine einfache Verteilung in eine komplexe Verteilung um, indem sie eine Reihe reversibler Transformationsfunktionen anwenden. Durch eine Reihe von Transformationen können gemäß dem Variablentransformationssatz die ursprünglichen Variablen wiederholt durch neue Variablen ersetzt werden und schließlich die Wahrscheinlichkeitsverteilung der endgültigen Zielvariablen erhalten.
Modelle des autoregressiven Flusses
Wenn eine Flusstransformation in einem normalisierten Fluss als autoregressives Modell dargestellt wird, bei dem jede Dimension in einer Vektorvariablen von der vorherigen Dimension abhängig ist, wird diese Änderung im Flussmodell als autoregressiver Fluss bezeichnet. Es ist ein Fortschritt gegenüber Modellen mit standardisierten Prozessen.
Häufig verwendete autoregressive Flussmodelle sind PixelCNN für die Bilderzeugung und WaveNet für eindimensionale Audiosignale. Sie bestehen alle aus einer Reihe kausaler Faltungen – Faltungsoperationen, die die Reihenfolge berücksichtigen: Vorhersagen zu einem bestimmten Zeitstempel verwenden nur in der Vergangenheit beobachtete Daten. In PixelCNN wird die kausale Faltung durch einen maskierten Kernel durchgeführt. Und WaveNet verschiebt die Ausgabe um mehrere Zeitstempel in die Zukunft.

Flussbasierte Modelle eignen sich konzeptionell sehr gut für die Modellierung komplexer Verteilungen, sind jedoch im Vergleich zu autoregressiven Modellen auf dem neuesten Stand der Technik durch Leistungsprobleme bei der Dichteschätzung eingeschränkt. Obwohl Flussmodelle als Alternative zu GANs zunächst gute Ergebnisse liefern können, besteht zwischen ihnen eine erhebliche Lücke bei den Trainingsrechenkosten, da flussbasierte Modelle um ein Vielfaches länger brauchen, um Bilder mit der gleichen Auflösung zu erzeugen wie GANs.
Zusammenfassung
Jeder Algorithmus hat seine Vorteile und Einschränkungen hinsichtlich Genauigkeit und Effizienz. Obwohl GANs und prozessbasierte Modelle im Allgemeinen bessere oder realitätsnähere Bilder erzeugen als VAE, bietet letzteres eine schnellere Zeit und eine bessere Parametereffizienz als prozessbasierte Modelle. Hier ist eine Vergleichszusammenfassung der drei Modelle:

Sie können Sehen Sie, dass GAN aufgrund seiner Parallelität sehr effizient ist, aber nicht umkehrbar ist. Im Gegensatz dazu sind Strömungsmodelle reversibel, aber nicht effizient, während vae reversibel und effizient ist, aber nicht parallel berechnet werden kann. Basierend auf diesen Merkmalen können wir Kompromisse zwischen Output, Trainingsprozess und Effizienz bei der tatsächlichen Nutzung eingehen.
Das obige ist der detaillierte Inhalt vonDetaillierter Vergleich der generativen Modelle VAE, GAN und flussbasierter Modelle. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1386
1386
 52
52
 Bytedance Cutting führt SVIP-Supermitgliedschaft ein: 499 Yuan für ein fortlaufendes Jahresabonnement, das eine Vielzahl von KI-Funktionen bietet
Jun 28, 2024 am 03:51 AM
Bytedance Cutting führt SVIP-Supermitgliedschaft ein: 499 Yuan für ein fortlaufendes Jahresabonnement, das eine Vielzahl von KI-Funktionen bietet
Jun 28, 2024 am 03:51 AM
Diese Seite berichtete am 27. Juni, dass Jianying eine von FaceMeng Technology, einer Tochtergesellschaft von ByteDance, entwickelte Videobearbeitungssoftware ist, die auf der Douyin-Plattform basiert und grundsätzlich kurze Videoinhalte für Benutzer der Plattform produziert Windows, MacOS und andere Betriebssysteme. Jianying kündigte offiziell die Aktualisierung seines Mitgliedschaftssystems an und führte ein neues SVIP ein, das eine Vielzahl von KI-Schwarztechnologien umfasst, wie z. B. intelligente Übersetzung, intelligente Hervorhebung, intelligente Verpackung, digitale menschliche Synthese usw. Preislich beträgt die monatliche Gebühr für das Clipping von SVIP 79 Yuan, die Jahresgebühr 599 Yuan (Hinweis auf dieser Website: entspricht 49,9 Yuan pro Monat), das fortlaufende Monatsabonnement beträgt 59 Yuan pro Monat und das fortlaufende Jahresabonnement beträgt 499 Yuan pro Jahr (entspricht 41,6 Yuan pro Monat). Darüber hinaus erklärte der Cut-Beamte auch, dass diejenigen, die den ursprünglichen VIP abonniert haben, das Benutzererlebnis verbessern sollen
 Kontexterweiterter KI-Codierungsassistent mit Rag und Sem-Rag
Jun 10, 2024 am 11:08 AM
Kontexterweiterter KI-Codierungsassistent mit Rag und Sem-Rag
Jun 10, 2024 am 11:08 AM
Verbessern Sie die Produktivität, Effizienz und Genauigkeit der Entwickler, indem Sie eine abrufgestützte Generierung und ein semantisches Gedächtnis in KI-Codierungsassistenten integrieren. Übersetzt aus EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, Autor JanakiramMSV. Obwohl grundlegende KI-Programmierassistenten natürlich hilfreich sind, können sie oft nicht die relevantesten und korrektesten Codevorschläge liefern, da sie auf einem allgemeinen Verständnis der Softwaresprache und den gängigsten Mustern beim Schreiben von Software basieren. Der von diesen Coding-Assistenten generierte Code eignet sich zur Lösung der von ihnen zu lösenden Probleme, entspricht jedoch häufig nicht den Coding-Standards, -Konventionen und -Stilen der einzelnen Teams. Dabei entstehen häufig Vorschläge, die geändert oder verfeinert werden müssen, damit der Code in die Anwendung übernommen wird
 Kann LLM durch Feinabstimmung wirklich neue Dinge lernen: Die Einführung neuen Wissens kann dazu führen, dass das Modell mehr Halluzinationen hervorruft
Jun 11, 2024 pm 03:57 PM
Kann LLM durch Feinabstimmung wirklich neue Dinge lernen: Die Einführung neuen Wissens kann dazu führen, dass das Modell mehr Halluzinationen hervorruft
Jun 11, 2024 pm 03:57 PM
Large Language Models (LLMs) werden auf riesigen Textdatenbanken trainiert und erwerben dort große Mengen an realem Wissen. Dieses Wissen wird in ihre Parameter eingebettet und kann dann bei Bedarf genutzt werden. Das Wissen über diese Modelle wird am Ende der Ausbildung „verdinglicht“. Am Ende des Vortrainings hört das Modell tatsächlich auf zu lernen. Richten Sie das Modell aus oder verfeinern Sie es, um zu erfahren, wie Sie dieses Wissen nutzen und natürlicher auf Benutzerfragen reagieren können. Aber manchmal reicht Modellwissen nicht aus, und obwohl das Modell über RAG auf externe Inhalte zugreifen kann, wird es als vorteilhaft angesehen, das Modell durch Feinabstimmung an neue Domänen anzupassen. Diese Feinabstimmung erfolgt mithilfe von Eingaben menschlicher Annotatoren oder anderer LLM-Kreationen, wobei das Modell auf zusätzliches Wissen aus der realen Welt trifft und dieses integriert
 Sieben coole technische Interviewfragen für GenAI und LLM
Jun 07, 2024 am 10:06 AM
Sieben coole technische Interviewfragen für GenAI und LLM
Jun 07, 2024 am 10:06 AM
Um mehr über AIGC zu erfahren, besuchen Sie bitte: 51CTOAI.x Community https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou unterscheidet sich von der traditionellen Fragendatenbank, die überall im Internet zu sehen ist erfordert einen Blick über den Tellerrand hinaus. Large Language Models (LLMs) gewinnen in den Bereichen Datenwissenschaft, generative künstliche Intelligenz (GenAI) und künstliche Intelligenz zunehmend an Bedeutung. Diese komplexen Algorithmen verbessern die menschlichen Fähigkeiten, treiben Effizienz und Innovation in vielen Branchen voran und werden zum Schlüssel für Unternehmen, um wettbewerbsfähig zu bleiben. LLM hat ein breites Anwendungsspektrum und kann in Bereichen wie der Verarbeitung natürlicher Sprache, der Textgenerierung, der Spracherkennung und Empfehlungssystemen eingesetzt werden. Durch das Lernen aus großen Datenmengen ist LLM in der Lage, Text zu generieren
 Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Maschinelles Lernen ist ein wichtiger Zweig der künstlichen Intelligenz, der Computern die Möglichkeit gibt, aus Daten zu lernen und ihre Fähigkeiten zu verbessern, ohne explizit programmiert zu werden. Maschinelles Lernen hat ein breites Anwendungsspektrum in verschiedenen Bereichen, von der Bilderkennung und der Verarbeitung natürlicher Sprache bis hin zu Empfehlungssystemen und Betrugserkennung, und es verändert unsere Lebensweise. Im Bereich des maschinellen Lernens gibt es viele verschiedene Methoden und Theorien, von denen die fünf einflussreichsten Methoden als „Fünf Schulen des maschinellen Lernens“ bezeichnet werden. Die fünf Hauptschulen sind die symbolische Schule, die konnektionistische Schule, die evolutionäre Schule, die Bayes'sche Schule und die Analogieschule. 1. Der Symbolismus, auch Symbolismus genannt, betont die Verwendung von Symbolen zum logischen Denken und zum Ausdruck von Wissen. Diese Denkrichtung glaubt, dass Lernen ein Prozess der umgekehrten Schlussfolgerung durch das Vorhandene ist
 Um ein neues wissenschaftliches und komplexes Frage-Antwort-Benchmark- und Bewertungssystem für große Modelle bereitzustellen, haben UNSW, Argonne, die University of Chicago und andere Institutionen gemeinsam das SciQAG-Framework eingeführt
Jul 25, 2024 am 06:42 AM
Um ein neues wissenschaftliches und komplexes Frage-Antwort-Benchmark- und Bewertungssystem für große Modelle bereitzustellen, haben UNSW, Argonne, die University of Chicago und andere Institutionen gemeinsam das SciQAG-Framework eingeführt
Jul 25, 2024 am 06:42 AM
Herausgeber | Der Frage-Antwort-Datensatz (QA) von ScienceAI spielt eine entscheidende Rolle bei der Förderung der Forschung zur Verarbeitung natürlicher Sprache (NLP). Hochwertige QS-Datensätze können nicht nur zur Feinabstimmung von Modellen verwendet werden, sondern auch effektiv die Fähigkeiten großer Sprachmodelle (LLMs) bewerten, insbesondere die Fähigkeit, wissenschaftliche Erkenntnisse zu verstehen und zu begründen. Obwohl es derzeit viele wissenschaftliche QS-Datensätze aus den Bereichen Medizin, Chemie, Biologie und anderen Bereichen gibt, weisen diese Datensätze immer noch einige Mängel auf. Erstens ist das Datenformular relativ einfach, die meisten davon sind Multiple-Choice-Fragen. Sie sind leicht auszuwerten, schränken jedoch den Antwortauswahlbereich des Modells ein und können die Fähigkeit des Modells zur Beantwortung wissenschaftlicher Fragen nicht vollständig testen. Im Gegensatz dazu offene Fragen und Antworten
 SOTA Performance, eine multimodale KI-Methode zur Vorhersage der Protein-Ligand-Affinität in Xiamen, kombiniert erstmals molekulare Oberflächeninformationen
Jul 17, 2024 pm 06:37 PM
SOTA Performance, eine multimodale KI-Methode zur Vorhersage der Protein-Ligand-Affinität in Xiamen, kombiniert erstmals molekulare Oberflächeninformationen
Jul 17, 2024 pm 06:37 PM
Herausgeber |. KX Im Bereich der Arzneimittelforschung und -entwicklung ist die genaue und effektive Vorhersage der Bindungsaffinität von Proteinen und Liganden für das Arzneimittelscreening und die Arzneimitteloptimierung von entscheidender Bedeutung. Aktuelle Studien berücksichtigen jedoch nicht die wichtige Rolle molekularer Oberflächeninformationen bei Protein-Ligand-Wechselwirkungen. Auf dieser Grundlage schlugen Forscher der Universität Xiamen ein neuartiges Framework zur multimodalen Merkmalsextraktion (MFE) vor, das erstmals Informationen über Proteinoberfläche, 3D-Struktur und -Sequenz kombiniert und einen Kreuzaufmerksamkeitsmechanismus verwendet, um verschiedene Modalitäten zu vergleichen Ausrichtung. Experimentelle Ergebnisse zeigen, dass diese Methode bei der Vorhersage von Protein-Ligand-Bindungsaffinitäten Spitzenleistungen erbringt. Darüber hinaus belegen Ablationsstudien die Wirksamkeit und Notwendigkeit der Proteinoberflächeninformation und der multimodalen Merkmalsausrichtung innerhalb dieses Rahmens. Verwandte Forschungen beginnen mit „S
 SK Hynix wird am 6. August neue KI-bezogene Produkte vorstellen: 12-Layer-HBM3E, 321-High-NAND usw.
Aug 01, 2024 pm 09:40 PM
SK Hynix wird am 6. August neue KI-bezogene Produkte vorstellen: 12-Layer-HBM3E, 321-High-NAND usw.
Aug 01, 2024 pm 09:40 PM
Laut Nachrichten dieser Website vom 1. August hat SK Hynix heute (1. August) einen Blogbeitrag veröffentlicht, in dem es ankündigt, dass es am Global Semiconductor Memory Summit FMS2024 teilnehmen wird, der vom 6. bis 8. August in Santa Clara, Kalifornien, USA, stattfindet viele neue Technologien Generation Produkt. Einführung des Future Memory and Storage Summit (FutureMemoryandStorage), früher Flash Memory Summit (FlashMemorySummit), hauptsächlich für NAND-Anbieter, im Zusammenhang mit der zunehmenden Aufmerksamkeit für die Technologie der künstlichen Intelligenz wurde dieses Jahr in Future Memory and Storage Summit (FutureMemoryandStorage) umbenannt Laden Sie DRAM- und Speicheranbieter und viele weitere Akteure ein. Neues Produkt SK Hynix wurde letztes Jahr auf den Markt gebracht



