

https://www.zhuanzhi.ai/paper/a904f0aa0762e65e1dd0b8b464df7168#🎜 🎜## 🎜🎜#
Grafiken sind wichtige Datendarstellungen, die Objekte und ihre Beziehungen beschreiben und in einer Vielzahl realer Szenarien vorkommen. Die Diagrammerstellung ist eines der Hauptprobleme in diesem Bereich, bei dem es darum geht, die Verteilung eines bestimmten Diagramms zu lernen und weitere neue Diagramme zu generieren. Aufgrund ihrer weit verbreiteten Anwendung werden generative Modelle von Graphen mit einer reichen Geschichte jedoch traditionell handgefertigt und können nur einige statistische Eigenschaften von Graphen modellieren.Die jüngsten Fortschritte bei tiefen generativen Modellen für die Graphgenerierung sind ein wichtiger Schritt zur Verbesserung der Genauigkeit generierter Graphen und ebnen den Weg für neue Arten von Anwendungen. Dieses Papier bietet einen umfassenden Überblick über die Literatur im Bereich tiefer generativer Modelle für die Graphgenerierung. Erstens werden die formale Definition und das vorläufige Wissen von tiefen generativen Modellen für die Graphgenerierung gegeben; zweitens wird die Klassifizierung von tiefen generativen Modellen für die bedingungslose und bedingte Graphengenerierung vorgeschlagen und die vorhandenen Arbeiten jedes einzelnen verglichen und analysiert. Anschließend wird ein Überblick über die Bewertungsmaßstäbe in diesem speziellen Bereich gegeben. Abschließend werden die Anwendungen der Tiefenkartengenerierung zusammengefasst und fünf vielversprechende Forschungsrichtungen aufgezeigt.
Einführung
Grafiken sind in der realen Welt allgegenwärtig und repräsentieren Objekte und ihre Beziehungen, beispielsweise in der Gesellschaft Netzwerke, Zitiernetzwerke, biologische Netzwerke, Transportnetzwerke usw. Es ist auch bekannt, dass Diagramme komplexe Strukturen aufweisen, die umfangreiche zugrunde liegende Werte enthalten [1]. Auf diesem Gebiet wurden erhebliche Anstrengungen unternommen, was zu einer reichhaltigen Literatur und Methoden zur Behandlung verschiedener Graphenprobleme führte.Diese Aufgaben können in zwei Kategorien unterteilt werden: 1) Vorhersage und Analyse von Mustern eines bestimmten Diagramms. 2) Lernen Sie die Verteilung eines bestimmten Diagramms kennen und erstellen Sie weitere neuartige Diagramme. Der erste Typ deckt viele Forschungsbereiche ab, einschließlich Knotenklassifizierung, Diagrammklassifizierung und Linkvorhersage. In diesem Bereich wurde in den letzten Jahrzehnten viel getan. Im Vergleich zur ersten Art von Problemen bezieht sich die zweite Art von Problemen auf Probleme bei der Diagrammgenerierung, auf die sich dieser Artikel ebenfalls konzentriert.
Die Diagrammerstellung umfasst den Prozess der Modellierung und Generierung realer Diagramme, der in verschiedenen Bereichen Anwendung findet, beispielsweise beim Verständnis sozialer Netzwerke [2], [3], interaktive Dynamik in [4], Anomalieerkennung [5], Proteinstrukturmodellierung [6], [7], Quellcodegenerierung und -übersetzung [8], [9], semantisches Parsen [10]. Aufgrund ihrer breiten Anwendung hat die Entwicklung generativer Graphenmodelle eine lange Geschichte und führte zu bekannten Modellen wie Zufallsgraphen, Kleinweltmodellen, stochastischen Blockmodellen und Bayes'schen Netzwerkmodellen, die auf A-priori-Strukturen basieren Annahmen [11] Diagramm erstellen. Diese graphgenerativen Modelle [12], [13], [14] zielen darauf ab, vorab ausgewählte Graphfamilien wie Zufallsgraphen [15], Small-World-Netzwerke [16] und skalenfreie Graphen [12] zu modellieren. Aufgrund ihrer Einfachheit und ihres handgefertigten Charakters sind diese Zufallsgraphenmodelle jedoch häufig nur begrenzt in der Lage, komplexe Abhängigkeiten zu modellieren, und können nur einige statistische Eigenschaften des Graphen modellieren.
Diese Methoden funktionieren normalerweise gut für die Eigenschaften, auf die die vordefinierten Prinzipien zugeschnitten sind, funktionieren jedoch normalerweise nicht gut für andere Eigenschaften. Beispielsweise können Kontaktnetzwerkmodelle für Grippeepidemien geeignet sein, nicht jedoch für dynamische funktionale Konnektivität. In vielen Bereichen sind die Natur und die generativen Prinzipien von Netzwerken jedoch weitgehend unbekannt, beispielsweise zur Erklärung der Mechanismen von psychischen Erkrankungen, Cyberangriffen und der Verbreitung von Malware in Gehirnnetzwerken. Ein weiteres Beispiel: Der Erdos-Renyi-Graph weist nicht die ausgeprägte Gradverteilung auf, die für viele Netzwerke in der realen Welt typisch ist. Darüber hinaus schränkt die Verwendung von A-priori-Annahmen diese traditionellen Techniken bei der Erforschung weiterer Anwendungen in größeren Bereichen ein, in denen A-priori-Kenntnisse über Graphen immer nicht verfügbar sind.
Angesichts der Einschränkungen traditioneller Graphgenerierungstechniken besteht eine wichtige offene Herausforderung darin, Methoden zu entwickeln, mit denen generative Modelle direkt aus einer Sammlung beobachteter Graphen gelernt werden können, was wichtig ist Schritt zur Verbesserung der Wiedergabetreue generierter Diagramme. Es ebnet den Weg für neue Arten von Anwendungen, wie etwa die Entdeckung neuer Medikamente [17], [18] und die Modellierung der Proteinstruktur [19], [20], [21]. Jüngste Fortschritte bei tiefen generativen Modellen wie Variational Autoencoders (VAEs) [22] und generativen gegnerischen Netzwerken (GANs) [23] wurden für die Generierung von Graphen vorgeschlagen. Viele Deep-Learning-Modelle wurden für die Generierung von Graphen formalisiert tiefe generative Modelle, die im Mittelpunkt dieser Überprüfung stehen.
Verschiedene fortgeschrittene Arbeiten wurden in der Tiefenkartengenerierung durchgeführt, von der einmaligen Diagrammgenerierung bis hin zu sequentiellen Diagrammgenerierungsprozessen, unter Anpassung an verschiedene tiefe generative Lernstrategien. Diese Methoden zielen darauf ab, eine oder mehrere der oben genannten Herausforderungen durch Arbeiten in verschiedenen Bereichen anzugehen, darunter maschinelles Lernen, Bioinformatik, künstliche Intelligenz, menschliche Gesundheit und Social Network Mining. Allerdings verwenden in unterschiedlichen Forschungsbereichen entwickelte Methoden häufig unterschiedliche Vokabeln und gehen Probleme aus unterschiedlichen Perspektiven an. Darüber hinaus mangelt es an standardisierten und umfassenden Bewertungsverfahren zur Validierung der entwickelten tiefen generativen Modelle für Graphen. Zu diesem Zweck bietet dieser Artikel einen systematischen Überblick über tiefe generative Modelle für die Graphgenerierung. Der Zweck besteht darin, interdisziplinären Forschern bei der Auswahl geeigneter Technologien zur Lösung von Problemen in ihren Anwendungsfeldern zu helfen und, was noch wichtiger ist, Forschern im Bereich der Graphgenerierung dabei zu helfen, die Grundprinzipien der Graphgenerierung zu verstehen und offene Forschungsmöglichkeiten im Bereich der Deep-Graph-Generierung zu identifizieren. Nach unserem besten Wissen ist dies die erste umfassende Übersicht über tiefgreifende generative Modelle für die Graphgenerierung. Nachfolgend fassen wir die Hauptbeiträge dieser Rezension zusammen: Dieses Papier schlägt eine Taxonomie tiefer generativer Modelle für die Graphgenerierung vor, klassifiziert nach Problemstellung und Ansatz. Die Vor- und Nachteile sowie Zusammenhänge zwischen den verschiedenen Unterkategorien werden dargestellt. Tiefe generative Modelle zur Graphgenerierung und grundlegende tiefe generative Modelle werden ausführlich beschrieben, analysiert und verglichen. Der Zweck der Kartengenerierung mit bedingungsloser Tiefe besteht darin, einen Satz beobachteter realer Diagramme aus der realen Verteilung p(G) durch ein generatives Tiefenmodell abzutasten. Lernen Sie das Verteilung pmodel(G). Entsprechend dem Stil des Generierungsprozesses können wir diese Methoden in zwei Hauptzweige unterteilen: (1) sequentielle Generierung: Knoten und Kanten nacheinander generieren; (2) einmalige Generierung: Erstellen eines probabilistischen Diagrammmodells gemäß der Matrixdarstellung; und gleichzeitig Knoten und Kanten erzeugen. Beide Methoden zur Diagrammerstellung haben Vor- und Nachteile. Die sequentielle Generierung führt zwar die lokalen Entscheidungen der vorherigen Generation effizient aus, hat jedoch Schwierigkeiten, langfristige Abhängigkeiten aufrechtzuerhalten. Daher ist es schwierig, einige globale Eigenschaften von Diagrammen (z. B. skalenfreie Eigenschaften) einzubeziehen. Darüber hinaus beschränken sich bestehende Arbeiten zur Sequenzgenerierung auf die Reihenfolge vordefinierter Sequenzen und lassen die Rolle von Permutationen außer Acht. One-Shot-Generierungsmethoden können den gesamten Graphen (d. h. Knoten und Kanten) durch mehrere Iterationen gleichzeitig generieren und verfeinern und so die globalen Eigenschaften des Graphen modellieren. Sie sind jedoch zeitaufwändig, da die globalen Beziehungen zwischen Knoten kollektiv modelliert werden müssen Die Komplexität übersteigt normalerweise O(N2), was die Skalierung der meisten Methoden auf große Diagramme erschwert. Das Ziel der Diagrammgenerierung mit bedingter Tiefe besteht darin, das bedingte Verteilungsmodell (G|y) zu lernen. Hilfsinformationen können Kategoriebezeichnungen, semantischer Kontext, Diagramme aus anderen Verbreitungsräumen usw. sein. Im Vergleich zur bedingungslosen Tiefenkartengenerierung muss bei der bedingten Generierung zusätzlich zu den Herausforderungen bei der Kartengenerierung auch berücksichtigt werden, wie Merkmale aus bestimmten Bedingungen extrahiert und in die Kartengenerierung integriert werden. Um die vorhandenen Modelle zur Erzeugung bedingter Tiefenkarten systematisch einzuführen, beschreiben wir daher hauptsächlich, wie diese Methoden mit Bedingungen umgehen. Da Bedingungen jede Form von Hilfsinformationen sein können, werden sie in drei Typen unterteilt, darunter Diagramm, Sequenz und semantischer Kontext, wie im gelben Teil des Taxonomiebaums in Abbildung 1 dargestellt
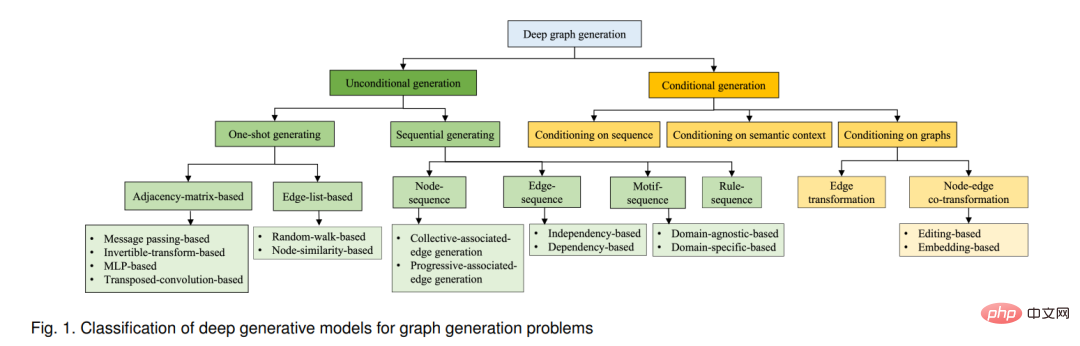
Generatives Modell mit unbedingter Tiefe für die Diagrammgenerierung
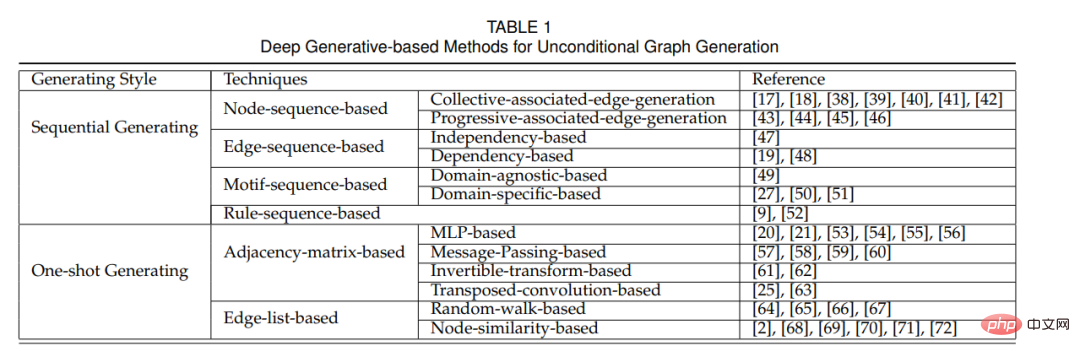
Generatives Modell mit bedingter Tiefe für die Diagrammgenerierung
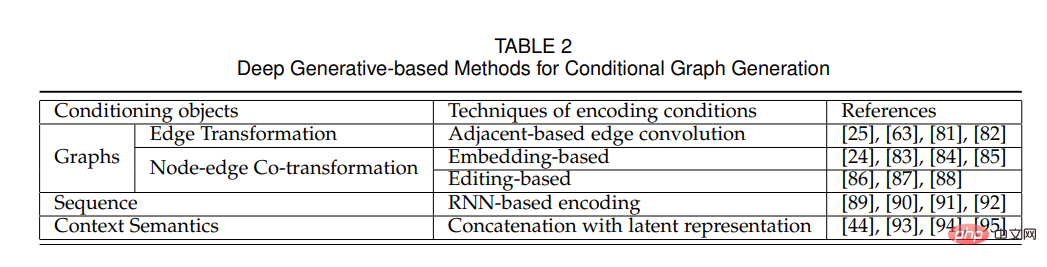
Das obige ist der detaillierte Inhalt vonWie erstelle ich „gute' Diagramme? Systematische Überprüfung tiefer generativer Modelle für die Graphgenerierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 So entsperren Sie Android-Berechtigungsbeschränkungen
So entsperren Sie Android-Berechtigungsbeschränkungen
 In der Sprache C gibt es mehrere Ausgabe- und Eingabefunktionen
In der Sprache C gibt es mehrere Ausgabe- und Eingabefunktionen
 Lösungen für unbekannte Software-Ausnahmen in Computeranwendungen
Lösungen für unbekannte Software-Ausnahmen in Computeranwendungen
 So verwenden Sie Spyder
So verwenden Sie Spyder
 Ripple-Handelsplattform
Ripple-Handelsplattform
 Was sind die Vorteile des Java-Factory-Musters?
Was sind die Vorteile des Java-Factory-Musters?
 Verwendung der Memcpy-Funktion
Verwendung der Memcpy-Funktion
 Welche Software ist Premiere?
Welche Software ist Premiere?




