Die Genauigkeit von GPT-3 beim Lösen mathematischer Probleme ist auf 92,5 % gestiegen! Microsoft schlägt MathPrompter vor, um „wissenschaftliche' Sprachmodelle ohne Feinabstimmung zu erstellen

Das am meisten kritisierte Manko großer Sprachmodelle ist neben ernsthaftem Unsinn wahrscheinlich ihre „Unfähigkeit, Mathematik zu machen“.

Zum Beispiel ein komplexes mathematisches Problem, das mehrstufiges Denken erfordert, Sprachmodelle können in der Regel keine korrekten Antworten geben. Selbst mit dem Segen der „Denkketten“-Technologie treten in den Zwischenschritten häufig Fehler auf.

Im Gegensatz zu Aufgaben zum Verstehen natürlicher Sprache in den Geisteswissenschaften gibt es bei Mathematikfragen normalerweise nur eine richtige Antwort, und der Antwortbereich ist nicht so offen, was die Aufgabe vereinfacht Es ist schwierig, genaue Lösungen zu generieren. Bei großen Sprachmodellen ist dies schwieriger.

Darüber hinaus bieten vorhandene Sprachmodelle bei mathematischen Problemen normalerweise keine Zuverlässigkeit für ihre Antworten, sodass Benutzer die Zuverlässigkeit der generierten Antworten nicht beurteilen können .

Um dieses Problem zu lösen, hat Microsoft Research die MathPrompter-Technologie vorgeschlagen, die die Leistung von LLM bei arithmetischen Problemen verbessern und gleichzeitig die Abhängigkeit von Vorhersagen erhöhen kann.

Papierlink: https://arxiv.org/abs/2303.05398

MathPrompter nutzt die Zero-Shot-Thinking-Chain-Prompting-Technologie, um mehrere algebraische Ausdrücke oder Python-Funktionen zu generieren, um dasselbe mathematische Problem auf unterschiedliche Weise zu lösen und so die Glaubwürdigkeit der Ausgabeergebnisse zu verbessern.

Im Vergleich zu anderen Hinweis-basierten CoT-Methoden prüft MathPrompter auch die Gültigkeit von Zwischenschritten.

Basierend auf 175B-Parameter-GPT, Verwendung der MathPrompter-Methode, um die Genauigkeit des MultiArith-Datensatzes von 78,7 % auf 92,5 % zu erhöhen!

Prompt mit Spezialisierung auf Mathematik

In den letzten Jahren wurde die Entwicklung der Verarbeitung natürlicher Sprache größtenteils großen Sprachmodellen (LLMs) zugeschrieben Aufgrund seiner kontinuierlichen Erweiterung hat es erstaunliche Zero-Shot- und Fence-Shot-Fähigkeiten bewiesen und auch zur Entwicklung der Eingabeaufforderungstechnologie beigetragen. Benutzer müssen nur ein paar einfache Proben in LLM eingeben, um Vorhersagen zu treffen. Man kann sagen, dass

prompt für Einzelschrittaufgaben recht erfolgreich ist, aber bei Aufgaben, die mehrstufiges Denken erfordern, ist die Leistung der Prompt-Technologie immer noch unzureichend.

Wenn Menschen ein komplexes Problem lösen, werden sie es aufschlüsseln und versuchen, es Schritt für Schritt zu lösen. Die „Chain of Thought“ (CoT)-Prompt-Technologie dient dazu Die Kombination dieser Intuition wird auf LLMs ausgeweitet, was zu Leistungsverbesserungen bei einer Reihe von NLP-Aufgaben führt, die Inferenz erfordern.

In diesem Artikel wird hauptsächlich die Zero-Shot-CoT-Methode „zur Lösung mathematischer Argumentationsaufgaben“ untersucht. Die Genauigkeit hat sich verbessert von 17,7 % auf 78,7 %, aber es gibt immer noch zwei wesentliche Mängel:

1. Die vom Modell verfolgte Denkkette hat zwar bessere Ergebnisse erzielt, wurde jedoch nicht überprüft die Gültigkeit jedes Schritts, gefolgt von der Denkkettenaufforderung;

2 Für die LLM-Vorhersageergebnisse wurde keine Zuverlässigkeit angegeben.

MathPrompter

Um diese Lücken bis zu einem gewissen Grad zu schließen, ließen sich Forscher von „der Art und Weise, wie Menschen mathematische Probleme lösen“ inspirieren und kombinierten Komplexe Probleme werden in einfachere mehrstufige Verfahren zerlegt und die Methoden werden bei jedem Schritt mit mehreren Mitteln validiert.

Da LLM ein generatives Modell ist, muss sichergestellt werden, dass die generierten Antworten korrekt sind, insbesondere für mathematische Bei Denkaufgaben wird es sehr knifflig.

Forscher beobachteten den Prozess, bei dem Schüler Rechenaufgaben lösten, und fassten mehrere Schritte zusammen, die Schüler zur Überprüfung ihrer Lösungen unternahmen:

Übereinstimmung mit bekannten Ergebnissen Durch den Vergleich der Lösung mit bekannten Ergebnissen können Sie deren Genauigkeit bewerten und erforderliche Anpassungen vornehmen. Dies ist besonders nützlich, wenn es sich bei dem Problem um ein Standardproblem handelt mit einer etablierten Lösung.

Mehrfache Überprüfung hilft, die Wirksamkeit der Lösung zu bestätigen, indem das Problem aus mehreren Blickwinkeln betrachtet und die Ergebnisse verglichen werden, um sicherzustellen, dass es wirksam ist sowohl vernünftig als auch genau.

Gegenprüfung, der Prozess der Lösung des Problems ist ebenso notwendig wie die endgültige Antwort; überprüfen Sie die Richtigkeit der Zwischenschritte in Der Prozess Der Denkprozess hinter der Lösung kann klar verstanden werden.

Rechnerüberprüfung Die Verwendung eines Taschenrechners oder Computers zur Durchführung arithmetischer Berechnungen kann dabei helfen, die Richtigkeit der endgültigen Antwort zu überprüfen# 🎜🎜#

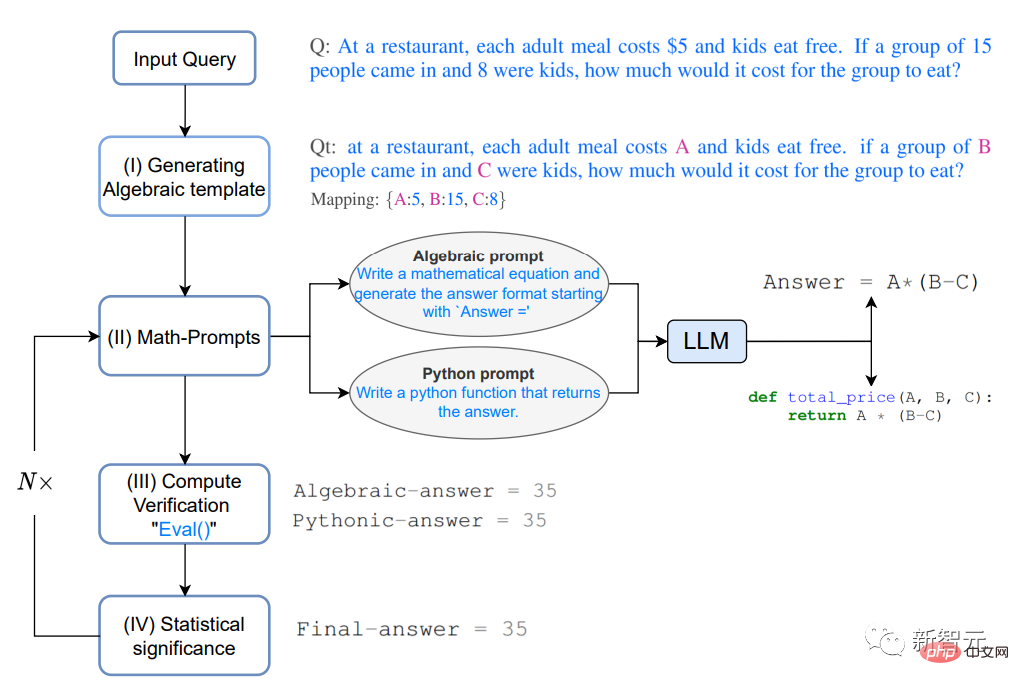
Insbesondere bei einer Frage Q: In einem Restaurant beträgt der Preis für jede Mahlzeit für Erwachsene 5 US-Dollar und Kinder essen kostenlos. Wenn 15 Personen reinkommen und 8 davon Kinder sind, wie viel kostet das Essen für diese Personengruppe? Generieren einer algebraischen Vorlage

#🎜 🎜#

Konvertieren Sie das Problem zunächst in algebraische Form, indem Sie die numerischen Elemente mithilfe der Schlüssel-Wert-Zuordnung durch Variablen ersetzen, und erhalten Sie dann das modifizierte Problem Qt

# 🎜🎜#

2. Mathematische Eingabeaufforderungen Basierend auf Basierend auf der Intuition, die der oben beschriebene Denkprozess der mehrfachen Validierung und Gegenprüfung bietet, werden zwei verschiedene Methoden zur Generierung von Analyselösungen für Qt verwendet, nämlich der algebraische Weg und der pythonische Weg. LLM erhält die folgenden Tipps, um zusätzlichen Qt-Kontext zu generieren.

Die Eingabeaufforderung kann „Leite einen algebraischen Ausdruck ab“ oder „Schreibe eine Python-Funktion“ lauten. # 🎜🎜#

Das LLM-Modell kann den folgenden Ausdruck ausgeben, nachdem es auf die Eingabeaufforderung reagiert hat.

Der oben generierte Analyseplan bietet Benutzern Tipps zum „Zwischendenkprozess“ von LLM und fügt zusätzliche Tipps hinzu kann die Genauigkeit und Konsistenz der Ergebnisse verbessern, was wiederum die Fähigkeit von MathPrompter verbessert, präzisere und effizientere Lösungen zu generieren. #? 🎜# Verwenden Sie mehrere zufällige Schlüsselwertzuordnungen von Eingabevariablen in Qt, um die im vorherigen Schritt generierten Ausdrücke auszuwerten, und verwenden Sie die eval()-Methode von Python, um diese Ausdrücke auszuwerten.

Vergleichen Sie dann die Ausgabeergebnisse, um zu sehen, ob Sie einen Konsens in der Antwort finden können, was auch ein höheres Maß an Sicherheit bieten kann, dass die Antwort richtig und zuverlässig ist.

Sobald der Ausdruck für die Ausgabe vereinbart ist, verwenden Sie die Eingabevariable Q Werte, um die endgültige Antwort zu berechnen.

4. Statistische Signifikanz

Um einen Konsens zu erzielen Um die Ausgabe für die verschiedenen Ausdrücke zu ermitteln, wiederholen Sie die Schritte 2 und 3 im Experiment etwa fünfmal und geben Sie den beobachteten Antwortwert an, der am häufigsten auftritt.

Wenn kein klarer Konsens besteht, wiederholen Sie die Schritte 2, 3 und 4.

Experimentelle Ergebnisse

Auswertung des MathPrompter am MultiArith-Datensatz, in dem mathematische Fragen speziell zum Testen von Modellen des maschinellen Lernens für komplexe Arithmetik entwickelt wurden. Fähigkeit zu operieren und zu argumentieren, was die Anwendung einer Vielzahl arithmetischer Operationen und logischen Denkens erfordert, um Probleme erfolgreich zu lösen.

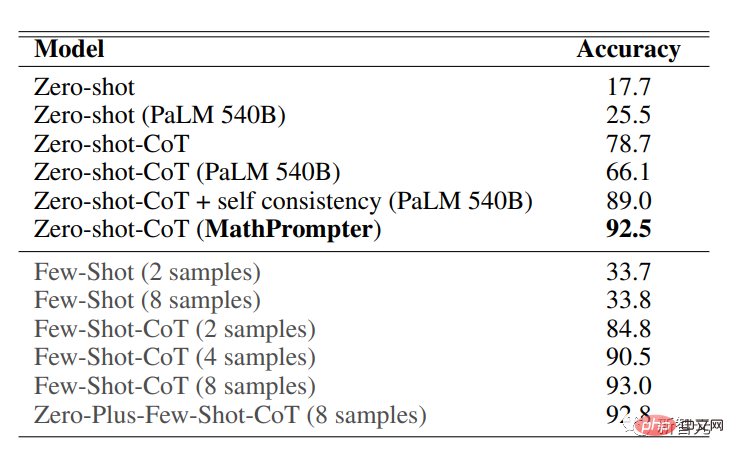
Die Genauigkeitsergebnisse des MultiArith-Datensatzes zeigen, dass die Leistung von MathPrompter besser ist als alle Zero-Shot- und Zero-Shot-CoT-Grundlinien, wodurch die Genauigkeit von 78,7 % auf 92,5 % erhöht wird des MathPrompter-Modells ist vergleichbar mit dem 540B-Parametermodell sowie der Few-shot-CoT-Methode von SOTA.

Wie Sie der obigen Tabelle entnehmen können, kann das Design von MathPrompter Um Probleme auszugleichen wie „Das Problem, dass die generierten Antworten manchmal einen Schritt daneben liegen, kann vermieden werden, indem das Modell mehrmals ausgeführt wird und Konsensergebnisse gemeldet werden.“

Darüber hinaus kann das Problem, dass der Argumentationsschritt möglicherweise zu lang ist, durch pythonische oder algebraische Methoden gelöst werden, die normalerweise weniger Token erfordern#🎜🎜 #

Darüber hinaus sind die Inferenzschritte möglicherweise korrekt, aber das endgültige Berechnungsergebnis ist falsch. MathPrompter löst dieses Problem mithilfe der Methodenfunktion eval() von Python.

In den meisten Fällen ist MathPrompter in der Lage, korrekte Zwischen- und Endantworten zu generieren, obwohl es einige Fälle gibt, wie zum Beispiel die letzte Frage in der Tabelle, die algebraisch sind und Pythonic Die Ausgabe ist konsistent, es gibt jedoch Fehler.

Das obige ist der detaillierte Inhalt vonDie Genauigkeit von GPT-3 beim Lösen mathematischer Probleme ist auf 92,5 % gestiegen! Microsoft schlägt MathPrompter vor, um „wissenschaftliche' Sprachmodelle ohne Feinabstimmung zu erstellen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!