Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 In einem Artikel wird kurz die Generalisierungsfähigkeit von Deep Learning erörtert
In einem Artikel wird kurz die Generalisierungsfähigkeit von Deep Learning erörtert
In einem Artikel wird kurz die Generalisierungsfähigkeit von Deep Learning erörtert

1. Das Problem der DNN-Generalisierungsfähigkeit
Der Artikel diskutiert hauptsächlich, warum das überparametrisierte neuronale Netzwerkmodell eine gute Generalisierungsleistung haben kann? Das heißt, es merkt sich nicht einfach den Trainingssatz, sondern fasst eine allgemeine Regel aus dem Trainingssatz zusammen, sodass diese an den Testsatz angepasst werden kann (Verallgemeinerungsfähigkeit).

Nehmen Sie das klassische Entscheidungsbaummodell als Beispiel: Wenn das Baummodell die allgemeinen Regeln des Datensatzes lernt: Eine gute Situation ist, dass der Baum, wenn er zuerst den Knoten teilt, nur Proben mit unterschiedlichen Bezeichnungen gut unterscheiden kann Da die Tiefe sehr gering ist und die entsprechende Anzahl von Stichproben auf jedem Blatt ausreicht (dh die auf statistischen Regeln basierende Datenmenge ist ebenfalls relativ groß), ist es wahrscheinlicher, dass die erhaltenen Regeln auf andere Daten verallgemeinert werden . (d. h. gute Anpassungsfähigkeit und Generalisierungsfähigkeit).
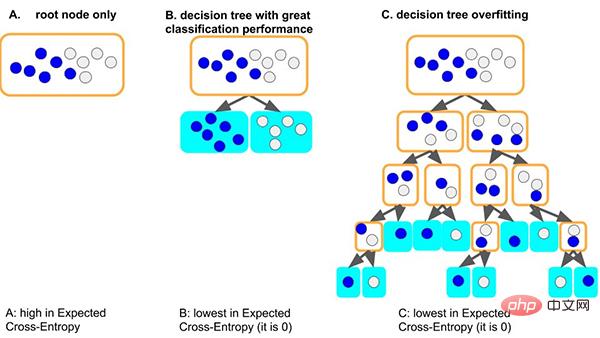
Eine weitere schlimmere Situation besteht darin, dass, wenn der Baum einige allgemeine Regeln nicht lernen kann, der Baum zum Erlernen dieses Datensatzes immer tiefer wird und jeder Blattknoten einer kleinen Anzahl von Stichproben (weniger) entsprechen kann Die durch die Daten gelieferten statistischen Informationen können nur Rauschen sein. Und schließlich müssen alle Daten auswendig gelernt werden (d. h. Überanpassung und keine Verallgemeinerungsfähigkeit). Wir können sehen, dass zu tiefe Baummodelle leicht überpassen können.
Wie kann also ein überparametrisiertes neuronales Netzwerk eine gute Generalisierung erreichen?
2. Die Gründe für die Generalisierungsfähigkeit von DNN
Dieser Artikel erläutert aus einer einfachen und allgemeinen Perspektive die Gründe für die Generalisierungsfähigkeit im Gradientenabstiegsoptimierungsprozess neuronaler Netze:
Wir haben die Gradientenkohärenztheorie zusammengefasst: Aus den Gradienten verschiedener Proben entsteht Kohärenz, weshalb neuronale Netze über gute Generalisierungsfähigkeiten verfügen. Wenn die Gradienten verschiedener Proben während des Trainings gut ausgerichtet sind, das heißt, wenn sie kohärent sind, ist der Gradientenabstieg stabil, kann schnell konvergieren und das resultierende Modell kann gut verallgemeinert werden. Andernfalls kann es zu keiner Verallgemeinerung kommen, wenn zu wenige Stichproben vorhanden sind oder die Trainingszeit zu lang ist.

Basierend auf dieser Theorie können wir die folgende Erklärung abgeben.
2.1 Generalisierung breiter neuronaler Netze
Modelle breiterer neuronaler Netze verfügen über gute Generalisierungsfähigkeiten. Dies liegt daran, dass größere Netzwerke über mehr Subnetzwerke verfügen und mit größerer Wahrscheinlichkeit eine Gradientenkohärenz erzeugen als kleinere Netzwerke, was zu einer besseren Generalisierung führt. Mit anderen Worten, der Gradientenabstieg ist ein Merkmalsselektor, der Generalisierungsgradienten (Kohärenzgradienten) priorisiert, und breitere Netzwerke können bessere Merkmale aufweisen, einfach weil sie mehr Merkmale haben.
- Originalarbeit: Generalisierung und Breite [2018b] haben herausgefunden, dass breitere Netzwerke auf jeder Ebene mehr Subnetzwerke haben mit maximaler Kohärenz in einem breiteren Netzwerk kann kohärenter sein als sein Gegenstück in einem dünneren Netzwerk und lässt sich daher besser verallgemeinern. Mit anderen Worten, da – wie in Abschnitt 10 erläutert – der Gradientenabstieg ein Merkmalsselektor ist, der eine gute Verallgemeinerung (kohärent) priorisiert. Breitere Netzwerke verfügen wahrscheinlich einfach deshalb über bessere Funktionen, weil sie über mehr Funktionen verfügen. Siehe in diesem Zusammenhang auch die Lottery Ticket Hypothesis [Frankle und Carbin, 2018]
- Papierlink: https://github.com/aialgorithm/Blog
Aber ich persönlich denke, es muss immer noch zwischen der Breite der Netzwerkeingabeschicht und der verborgenen Schicht unterschieden werden. Insbesondere für die Eingabeebene von Data-Mining-Aufgaben müssen Sie die Feature-Auswahl in Betracht ziehen (d. h. die Breite der Eingabeebene verringern), da die Eingabe-Features normalerweise manuell entworfen werden. Andernfalls wird die Gradientenkohärenz durch die direkte Eingabe von Feature-Rauschen beeinträchtigt . .
2.2 Generalisierung tiefer neuronaler Netze
Je tiefer das Netzwerk ist, desto stärker wird das Phänomen der Gradientenkohärenz und die Generalisierungsfähigkeit ist besser.

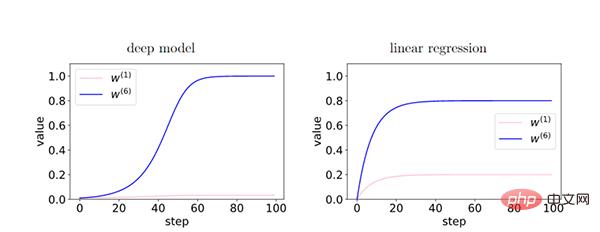
Da im Tiefenmodell die Rückkopplung zwischen den Schichten den kohärenten Gradienten stärkt, besteht während des Trainingsprozesses ein relativer Unterschied zwischen den Merkmalen des kohärenten Gradienten (W6) und den Merkmalen des inkohärenten Gradienten (W1) Exponentiell verstärkt. Dies führt dazu, dass tiefere Netzwerke kohärente Gradienten bevorzugen, was zu besseren Generalisierungsfähigkeiten führt.
2.3 Frühes Stoppen
Durch frühes Stoppen können wir den übermäßigen Einfluss inkohärenter Gradienten reduzieren und die Generalisierung verbessern.
Während des Trainings passen einige einfache Proben früher als andere Proben (harte Proben). In der frühen Trainingsphase dominiert der Korrelationsgradient dieser einfachen Stichproben und lässt sich leicht anpassen. In der späteren Trainingsphase dominiert der inkohärente Gradient schwieriger Proben den durchschnittlichen Gradienten g (wt), was zu einer schlechten Generalisierungsfähigkeit führt. Zu diesem Zeitpunkt ist es notwendig, frühzeitig aufzuhören.

- (Hinweis: Einfache Stichproben sind solche, die viele Steigungen im Datensatz gemeinsam haben. Aus diesem Grund sind die meisten Steigungen vorteilhaft und konvergieren schneller.)
2.4 Vollgradientenabstieg vs. Lernrate
Wir haben festgestellt, dass ein vollständiger Gradientenabstieg auch eine gute Generalisierungsfähigkeit aufweisen kann. Darüber hinaus zeigen sorgfältige Experimente, dass der stochastische Gradientenabstieg nicht unbedingt zu einer besseren Verallgemeinerung führt. Dies schließt jedoch nicht die Möglichkeit aus, dass stochastische Gradienten eher aus lokalen Minima herausspringen, eine Rolle bei der Regularisierung spielen usw.
- Basierend auf unserer Theorie sind endliche Lernrate und Mini-Batch-Stochastizität für die Generalisierung nicht erforderlich.
Wir glauben, dass eine niedrigere Lernrate den Generalisierungsfehler möglicherweise nicht verringert, da eine niedrigere Lernrate mehr Iterationen bedeutet (das Gegenteil des vorzeitigen Anhaltens).
- Unter der Annahme einer ausreichend kleinen Lernrate kann sich die Generalisierungslücke mit fortschreitendem Training nicht verringern. Dies folgt aus der iterativen Stabilitätsanalyse des Trainings: Mit 40 weiteren Schritten kann sich die Stabilität nur verschlechtern würde auf eine interessante Einschränkung der Theorie hinweisen. w) und der L2-Gradient ist w. Am Beispiel der L2-Regularisierung lautet die entsprechende Aktualisierungsformel für den Gradienten W(i+1): Bild
Wir können „L2-Regularisierung (Gewichtsabschwächung)“ als „Hintergrundkraft“ betrachten und jeden Parameter drücken nahe an einem datenunabhängigen Nullwert (mit L1 lässt sich leicht eine spärliche Lösung erhalten, mit L2 lässt sich leicht eine glatte Lösung nahe 0 erhalten), um den Einfluss in der Richtung des schwachen Gradienten zu eliminieren. Nur bei kohärenten Gradientenrichtungen können die Parameter relativ von der „Hintergrundkraft“ getrennt und die Gradientenaktualisierung auf Basis der Daten abgeschlossen werden.
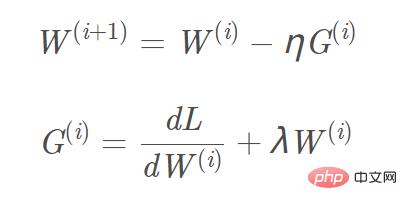
2.6 Weiterentwicklung des Gradientenabstiegsalgorithmus
 Momentum, Adam und andere Gradientenabstiegsalgorithmen
Momentum, Adam und andere Gradientenabstiegsalgorithmen
- Gradientenabstieg in schwachen Gradientenrichtungen unterdrücken
Zusammenfassung
Ein paar Worte am Ende des Artikels. Wenn Sie sich für die Theorie des Deep Learning interessieren, können Sie die im Artikel erwähnte verwandte Forschung lesen. 
Das obige ist der detaillierte Inhalt vonIn einem Artikel wird kurz die Generalisierungsfähigkeit von Deep Learning erörtert. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1382
1382
 52
52
 Methoden und Schritte zur Verwendung von BERT für die Stimmungsanalyse in Python
Jan 22, 2024 pm 04:24 PM
Methoden und Schritte zur Verwendung von BERT für die Stimmungsanalyse in Python
Jan 22, 2024 pm 04:24 PM
BERT ist ein vorab trainiertes Deep-Learning-Sprachmodell, das 2018 von Google vorgeschlagen wurde. Der vollständige Name lautet BidirektionalEncoderRepresentationsfromTransformers, der auf der Transformer-Architektur basiert und die Eigenschaften einer bidirektionalen Codierung aufweist. Im Vergleich zu herkömmlichen Einweg-Codierungsmodellen kann BERT bei der Textverarbeitung gleichzeitig Kontextinformationen berücksichtigen, sodass es bei Verarbeitungsaufgaben in natürlicher Sprache eine gute Leistung erbringt. Seine Bidirektionalität ermöglicht es BERT, die semantischen Beziehungen in Sätzen besser zu verstehen und dadurch die Ausdrucksfähigkeit des Modells zu verbessern. Durch Vorschulungs- und Feinabstimmungsmethoden kann BERT für verschiedene Aufgaben der Verarbeitung natürlicher Sprache verwendet werden, wie z. B. Stimmungsanalyse und Benennung
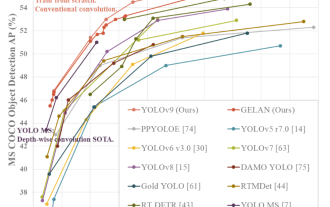 YOLO ist unsterblich! YOLOv9 wird veröffentlicht: Leistung und Geschwindigkeit SOTA~
Feb 26, 2024 am 11:31 AM
YOLO ist unsterblich! YOLOv9 wird veröffentlicht: Leistung und Geschwindigkeit SOTA~
Feb 26, 2024 am 11:31 AM
Heutige Deep-Learning-Methoden konzentrieren sich darauf, die am besten geeignete Zielfunktion zu entwerfen, damit die Vorhersageergebnisse des Modells der tatsächlichen Situation am nächsten kommen. Gleichzeitig muss eine geeignete Architektur entworfen werden, um ausreichend Informationen für die Vorhersage zu erhalten. Bestehende Methoden ignorieren die Tatsache, dass bei der schichtweisen Merkmalsextraktion und räumlichen Transformation der Eingabedaten eine große Menge an Informationen verloren geht. Dieser Artikel befasst sich mit wichtigen Themen bei der Datenübertragung über tiefe Netzwerke, nämlich Informationsengpässen und umkehrbaren Funktionen. Darauf aufbauend wird das Konzept der programmierbaren Gradienteninformation (PGI) vorgeschlagen, um die verschiedenen Änderungen zu bewältigen, die tiefe Netzwerke zur Erreichung mehrerer Ziele erfordern. PGI kann vollständige Eingabeinformationen für die Zielaufgabe zur Berechnung der Zielfunktion bereitstellen und so zuverlässige Gradienteninformationen zur Aktualisierung der Netzwerkgewichte erhalten. Darüber hinaus wird ein neues, leichtgewichtiges Netzwerk-Framework entworfen
 Latente Raumeinbettung: Erklärung und Demonstration
Jan 22, 2024 pm 05:30 PM
Latente Raumeinbettung: Erklärung und Demonstration
Jan 22, 2024 pm 05:30 PM
Latent Space Embedding (LatentSpaceEmbedding) ist der Prozess der Abbildung hochdimensionaler Daten auf niedrigdimensionalen Raum. Im Bereich des maschinellen Lernens und des tiefen Lernens handelt es sich bei der Einbettung latenter Räume normalerweise um ein neuronales Netzwerkmodell, das hochdimensionale Eingabedaten in einen Satz niedrigdimensionaler Vektordarstellungen abbildet. Dieser Satz von Vektoren wird oft als „latente Vektoren“ oder „latent“ bezeichnet Kodierungen". Der Zweck der Einbettung latenter Räume besteht darin, wichtige Merkmale in den Daten zu erfassen und sie in einer prägnanteren und verständlicheren Form darzustellen. Durch die Einbettung latenter Räume können wir Vorgänge wie das Visualisieren, Klassifizieren und Clustern von Daten im niedrigdimensionalen Raum durchführen, um die Daten besser zu verstehen und zu nutzen. Die Einbettung latenter Räume findet in vielen Bereichen breite Anwendung, z. B. bei der Bilderzeugung, der Merkmalsextraktion, der Dimensionsreduzierung usw. Die Einbettung des latenten Raums ist das Wichtigste
 Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Heute diskutieren wir darüber, wie Deep-Learning-Technologie die Leistung von visionbasiertem SLAM (Simultaneous Localization and Mapping) in komplexen Umgebungen verbessern kann. Durch die Kombination von Methoden zur Tiefenmerkmalsextraktion und Tiefenanpassung stellen wir hier ein vielseitiges hybrides visuelles SLAM-System vor, das die Anpassung in anspruchsvollen Szenarien wie schlechten Lichtverhältnissen, dynamischer Beleuchtung, schwach strukturierten Bereichen und starkem Jitter verbessern soll. Unser System unterstützt mehrere Modi, einschließlich erweiterter Monokular-, Stereo-, Monokular-Trägheits- und Stereo-Trägheitskonfigurationen. Darüber hinaus wird analysiert, wie visuelles SLAM mit Deep-Learning-Methoden kombiniert werden kann, um andere Forschungen zu inspirieren. Durch umfangreiche Experimente mit öffentlichen Datensätzen und selbst abgetasteten Daten demonstrieren wir die Überlegenheit von SL-SLAM in Bezug auf Positionierungsgenauigkeit und Tracking-Robustheit.
 Verstehen Sie in einem Artikel: die Zusammenhänge und Unterschiede zwischen KI, maschinellem Lernen und Deep Learning
Mar 02, 2024 am 11:19 AM
Verstehen Sie in einem Artikel: die Zusammenhänge und Unterschiede zwischen KI, maschinellem Lernen und Deep Learning
Mar 02, 2024 am 11:19 AM
In der heutigen Welle rasanter technologischer Veränderungen sind künstliche Intelligenz (KI), maschinelles Lernen (ML) und Deep Learning (DL) wie helle Sterne und führen die neue Welle der Informationstechnologie an. Diese drei Wörter tauchen häufig in verschiedenen hochaktuellen Diskussionen und praktischen Anwendungen auf, aber für viele Entdecker, die neu auf diesem Gebiet sind, sind ihre spezifische Bedeutung und ihre internen Zusammenhänge möglicherweise noch immer rätselhaft. Schauen wir uns also zunächst dieses Bild an. Es ist ersichtlich, dass zwischen Deep Learning, maschinellem Lernen und künstlicher Intelligenz ein enger Zusammenhang und eine fortschreitende Beziehung besteht. Deep Learning ist ein spezifischer Bereich des maschinellen Lernens und des maschinellen Lernens
 Super stark! Top 10 Deep-Learning-Algorithmen!
Mar 15, 2024 pm 03:46 PM
Super stark! Top 10 Deep-Learning-Algorithmen!
Mar 15, 2024 pm 03:46 PM
Fast 20 Jahre sind vergangen, seit das Konzept des Deep Learning im Jahr 2006 vorgeschlagen wurde. Deep Learning hat als Revolution auf dem Gebiet der künstlichen Intelligenz viele einflussreiche Algorithmen hervorgebracht. Was sind Ihrer Meinung nach die zehn besten Algorithmen für Deep Learning? Im Folgenden sind meiner Meinung nach die besten Algorithmen für Deep Learning aufgeführt. Sie alle nehmen hinsichtlich Innovation, Anwendungswert und Einfluss eine wichtige Position ein. 1. Hintergrund des Deep Neural Network (DNN): Deep Neural Network (DNN), auch Multi-Layer-Perceptron genannt, ist der am weitesten verbreitete Deep-Learning-Algorithmus. Als er erstmals erfunden wurde, wurde er aufgrund des Engpasses bei der Rechenleistung in Frage gestellt Jahre, Rechenleistung, Der Durchbruch kam mit der Datenexplosion. DNN ist ein neuronales Netzwerkmodell, das mehrere verborgene Schichten enthält. In diesem Modell übergibt jede Schicht Eingaben an die nächste Schicht und
 1,3 ms dauert 1,3 ms! Tsinghuas neueste Open-Source-Architektur für mobile neuronale Netzwerke RepViT
Mar 11, 2024 pm 12:07 PM
1,3 ms dauert 1,3 ms! Tsinghuas neueste Open-Source-Architektur für mobile neuronale Netzwerke RepViT
Mar 11, 2024 pm 12:07 PM
Papieradresse: https://arxiv.org/abs/2307.09283 Codeadresse: https://github.com/THU-MIG/RepViTRepViT funktioniert gut in der mobilen ViT-Architektur und zeigt erhebliche Vorteile. Als nächstes untersuchen wir die Beiträge dieser Studie. In dem Artikel wird erwähnt, dass Lightweight-ViTs bei visuellen Aufgaben im Allgemeinen eine bessere Leistung erbringen als Lightweight-CNNs, hauptsächlich aufgrund ihres Multi-Head-Selbstaufmerksamkeitsmoduls (MSHA), das es dem Modell ermöglicht, globale Darstellungen zu lernen. Allerdings wurden die architektonischen Unterschiede zwischen Lightweight-ViTs und Lightweight-CNNs noch nicht vollständig untersucht. In dieser Studie integrierten die Autoren leichte ViTs in die effektiven
 AlphaFold 3 wird auf den Markt gebracht und sagt die Wechselwirkungen und Strukturen von Proteinen und allen Lebensmolekülen umfassend und mit weitaus größerer Genauigkeit als je zuvor voraus
Jul 16, 2024 am 12:08 AM
AlphaFold 3 wird auf den Markt gebracht und sagt die Wechselwirkungen und Strukturen von Proteinen und allen Lebensmolekülen umfassend und mit weitaus größerer Genauigkeit als je zuvor voraus
Jul 16, 2024 am 12:08 AM
Herausgeber | Rettichhaut Seit der Veröffentlichung des leistungsstarken AlphaFold2 im Jahr 2021 verwenden Wissenschaftler Modelle zur Proteinstrukturvorhersage, um verschiedene Proteinstrukturen innerhalb von Zellen zu kartieren, Medikamente zu entdecken und eine „kosmische Karte“ jeder bekannten Proteininteraktion zu zeichnen. Gerade hat Google DeepMind das AlphaFold3-Modell veröffentlicht, das gemeinsame Strukturvorhersagen für Komplexe wie Proteine, Nukleinsäuren, kleine Moleküle, Ionen und modifizierte Reste durchführen kann. Die Genauigkeit von AlphaFold3 wurde im Vergleich zu vielen dedizierten Tools in der Vergangenheit (Protein-Ligand-Interaktion, Protein-Nukleinsäure-Interaktion, Antikörper-Antigen-Vorhersage) deutlich verbessert. Dies zeigt, dass dies innerhalb eines einzigen einheitlichen Deep-Learning-Frameworks möglich ist