Der Einstieg in die Graphentheorie ist eigentlich nicht schwer
Für Entwickler mit langjähriger Programmiererfahrung ist das Konzept von Diagrammen kein Unbekannter. Viele Top-Unternehmen testen in technischen Interviews ihr Verständnis der Graphentheorie. Tatsächlich müssen sich Entwickler nicht mit fortgeschrittenen Problemen befassen, um diese Konzepte nutzen zu können. Um dies zu verstehen, können wir zunächst untersuchen, warum Diagramme beliebte Datenstrukturen sind und wie man sie in Code implementiert.
Relationales Modell
Unabhängig von der Programmiererfahrung sollten Entwickler ein gewisses Verständnis für die Datentypen Array und Wörterbuch haben. Diese Sammlungen sind ein Standardkonzept, das in den meisten Sprachen verwendet wird und gut für die Darstellung von listenbasierten Inhalten geeignet ist:

In den meisten Fällen sind Listen die perfekte Lösung für die Anzeige von Informationen aus einer Datenbank oder einer REST-basierten Abfrage. Manchmal müssen Listen jedoch Datensätze bereitstellen, die einen zusammenhängenden Kontext haben. An diesem Punkt ist es praktisch, die Daten in Diagrammen zu organisieren.
Bei Diagrammen besteht das Hauptziel nicht darin, Informationen aufzulisten (obwohl dies möglich ist), sondern darin, Beziehungen zwischen Objekten zu definieren. Warum ist es sinnvoll, Beziehungen zwischen Objekten zu definieren? Schauen wir uns die folgenden Beispiele an. (1) Kartenanwendung wie Apple oder Google Maps)? Das von Ihnen erstellte Modell stellt nicht nur eine Liste aller bekannten Straßen in einer Datenbank bereit, sondern muss auch anhand von Faktoren wie Tageszeit, Verkehr und Einbahnstraßen ermitteln, wie Sie Ihr Ziel am besten erreichen. Damit diese große Datenmenge funktioniert, müssen Sie die Beziehung zwischen einer Straße und allen anderen Straßen im Modell kennen.
 (2) Soziale Medien
(2) Soziale Medien
Der Wert eines sozialen Mediums wird normalerweise an der Anzahl der Benutzer gemessen, die dem Benutzer folgen oder folgen. Webplattformen wie Twitter ziehen eine große Anzahl von Nutzern an, indem sie es ihnen ermöglichen, mit jedem in Kontakt zu treten und die neuesten Updates zu erhalten.
Das LinkedIn-Modell ist detaillierter, da ein Benutzer niemanden zu seinem Netzwerk hinzufügen kann, es sei denn, der Empfänger akzeptiert die Verbindungsanfrage des Benutzers. In diesem Fall handelt es sich bei der LinkedIn-Verbindung um eine wechselseitige Beziehung. In diesem Sinne können Benutzer auch ihr Netzwerk durchsuchen, um zu sehen, ob jemand mit der von ihnen gewünschten Stellenausschreibung in Verbindung steht. Unter „Netzwerk“ können in diesem Zusammenhang direkte oder indirekte Verbindungen verstanden werden. Ein solch leistungsstarkes Modell basiert nicht nur auf einer einfachen Liste, es enthält auch die Intelligenz, um zu bestimmen, wie alle Profile zusammenhängen.Grafikkomponenten
Da wir nun verstehen, wie Diagramme in alltäglichen Anwendungen verwendet werden, stellen wir die Komponenten von Diagrammen vor. Die Knoten im Diagramm werden als Eckpunkte bezeichnet. Während Diagramme als einzelne Eckpunkte erstellt werden können, repräsentieren Modelle mit mehreren Eckpunkten besser reale Anwendungen.Objekte in einem Diagramm sind über Verbindungen, sogenannte Kanten, miteinander verbunden.
Je nach Bedarf kann ein Scheitelpunkt über Kanten mit einem oder mehreren Objekten verbunden werden, oder Sie können einen Scheitelpunkt ohne Kanten erstellen. Schließlich haben Diagramme im Gegensatz zu anderen Standardstrukturen wie Stapeln oder Warteschlangen normalerweise keinen festgelegten Start- oder Endpunkt. Hier sind einige Beispiele für Diagrammkonfigurationen:Ein ungerichteter Graph mit zwei Eckpunkten und einer Kante
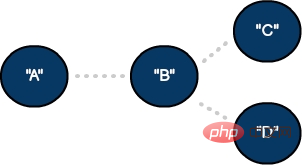
Ein ungerichteter Graph mit zwei Eckpunkten und einer Kante
 #🎜 🎜## 🎜🎜#
#🎜 🎜## 🎜🎜#
Gerichtet und ungerichtet
Im ungerichteten Diagramm sind die Verbindungen zwischen Quelle Scheitelpunkte und Ziele sind gleich. Diese Modelle stellen bidirektionale Verbindungen dar – ähnlich wie bidirektionale Straßen in Kartenanwendungen.
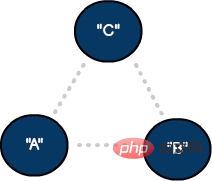
Um eine Einwegverbindung zu definieren, können wir das Modell mithilfe von Linien und Pfeilen in einen gerichteten Graphen aktualisieren: 🎜#Gerichteter Graph mit drei Eckpunkten und drei Kanten
#🎜 🎜#
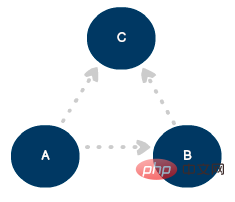 Konnektivitätsebene
Konnektivitätsebene
Manchmal müssen wir den Grad der Konnektivität zwischen Eckpunkten im Diagramm darstellen. Diese Technik eignet sich gut zur Quantifizierung von Entfernung, Zeit oder Schweregrad zwischen Knoten. Das Gewicht ist normalerweise einer Kante zugeordnet und dient als Vergleichsvariable zur Nachverfolgung.
.
Ein gerichteter Graph mit drei Eckpunkten und drei Kanten, wobei die Kanten gewichtet sind#🎜🎜 #
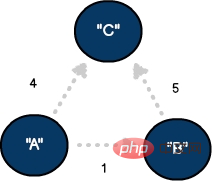 GraphVertex
GraphVertex
Mit einem grundlegenden Verständnis der Graphentheorie wollen wir sehen, wie man diese Modelle im Code repliziert. Nachfolgend erstellen wir einen Scheitelpunkt, der ein benutzerdefiniertes generisches Objekt (T) unterstützt. Eine tvalue-Variable stellt Daten dieses Typs dar, einschließlich einer einzelnen Zeichenfolge, int oder eines benutzerdefinierten Typs (z. B. eines Straßennamens oder eines Social-Media-Profils). Achten Sie außerdem darauf, dass unser Typ dem beliebten Equatable-Protokoll (Swift) entspricht. Dadurch können wir bei Bedarf bestimmte Scheitelpunktinstanzen auf Gleichheit vergleichen.
public class Vertex <t> : Equatable {<br><br>var tvalue: T?<br>var neighbors = Array<edge>>()<br>let uuid = UUID()<br><br>public init(with name: T) {<br>self.tvalue = name<br>}<br><br>//equatable conformance<br>public static func == (lhs: Vertex, rhs: Vertex) -> Bool {<br> return lhs.uuid == rhs.uuid<br>}<br>}</edge></t>
Adjacency.listAdja Cency-Listen-Darstellung Verbindungen zu anderen Eckpunkten. Wie bereits erwähnt, kann jeder Scheitelpunkt mit einem oder mehreren benachbarten Scheitelpunkten verbunden sein. Diese Liste von Beziehungen wird manchmal als „Adjazenzliste“ bezeichnet und kann zur Lösung vieler komplexerer Probleme verwendet werden.
var neighbors = Array<edge>>()</edge>
Graphedge
Beim Erstellen eines Scheitelpunkts haben wir eine Adjacency-Eigenschaft hinzugefügt, um ein Array benutzerdefinierter Kantentypen zu speichern. Die nächste Kante bietet eine Referenz für nachfolgende benachbarte Scheitelpunkte und ihre potenziellen Kantengewichte. 🎜🎜 Wir nennen es die grafische Leinwand. Obwohl unsere Leinwand technisch gesehen ein Array ist, ist es unser Ziel, die Sammlung als eine Reihe von Beziehungen zu visualisieren. Mit der Funktion „addVertex“ können wir der Leinwand einen einzelnen generischen Scheitelpunkt hinzufügen, während die Methode „addEdge“ die für die Kante benötigten Referenzinformationen bereitstellt. Schließlich geht unser Code davon aus, dass der Graph gerichtet ist, da Kanten (nur) zur Adjazenzliste der Quellscheitelpunkte hinzugefügt werden.public class Edge <t> {<br><br>var neighbor: Vertex<t><br>var weight: Int<br><br>init() {<br> weight = 0<br> self.neighbor = Vertex<t>()<br>}<br>}</t></t></t>Zusammenfassend haben wir Ihnen Diagramme vorgestellt und gesehen, wie sie zur Darstellung von Beziehungen zwischen Objekten verwendet werden können. Außerdem haben wir verschiedene Möglichkeiten zur Konfiguration von Diagrammen und die zur Beschreibung verschiedener Modelle verwendeten Komponenten untersucht.
Sobald das Modell definiert ist, legen wir den Grundstein für erweiterte Funktionen, einschließlich Diagrammnavigation und Traversalalgorithmen wie die Breitensuche.
Übersetzer-Einführung
Kang Shaojing, 51CTO-Community-Redakteur, ist derzeit in der Kommunikationsbranche tätig und arbeitet in untergeordneten Positionen in der Treiberentwicklung. Er hat Datenstrukturen und Python studiert und interessiert sich jetzt für Betriebssysteme, Datenbanken und andere verwandte Themen Felder.
Originaltitel: Der komplette Anfängerleitfaden zur Graphentheorie, Autor: Wayne Bishop
Link:
https://stackoverflow.blog/2022/05/26/the-complete-beginners-guide-to-graph-theory /
Das obige ist der detaillierte Inhalt vonDer Einstieg in die Graphentheorie ist eigentlich nicht schwer. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1379
1379
 52
52
 Ich habe versucht, die Vibe -Codierung mit Cursor AI und es ist erstaunlich!
Mar 20, 2025 pm 03:34 PM
Ich habe versucht, die Vibe -Codierung mit Cursor AI und es ist erstaunlich!
Mar 20, 2025 pm 03:34 PM
Die Vibe -Codierung verändert die Welt der Softwareentwicklung, indem wir Anwendungen mit natürlicher Sprache anstelle von endlosen Codezeilen erstellen können. Inspiriert von Visionären wie Andrej Karpathy, lässt dieser innovative Ansatz Dev
 Top 5 Genai Starts vom Februar 2025: GPT-4,5, GROK-3 & MEHR!
Mar 22, 2025 am 10:58 AM
Top 5 Genai Starts vom Februar 2025: GPT-4,5, GROK-3 & MEHR!
Mar 22, 2025 am 10:58 AM
Februar 2025 war ein weiterer bahnbrechender Monat für die Generative KI, die uns einige der am meisten erwarteten Modell-Upgrades und bahnbrechenden neuen Funktionen gebracht hat. Von Xais Grok 3 und Anthropics Claude 3.7 -Sonett, um g zu eröffnen
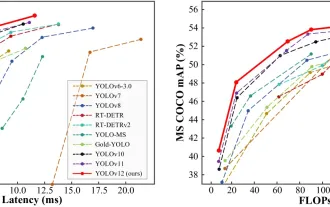 Wie benutze ich Yolo V12 zur Objekterkennung?
Mar 22, 2025 am 11:07 AM
Wie benutze ich Yolo V12 zur Objekterkennung?
Mar 22, 2025 am 11:07 AM
Yolo (Sie schauen nur einmal) war ein führender Echtzeit-Objekterkennungsrahmen, wobei jede Iteration die vorherigen Versionen verbessert. Die neueste Version Yolo V12 führt Fortschritte vor, die die Genauigkeit erheblich verbessern
 Beste KI -Kunstgeneratoren (kostenlos & amp; bezahlt) für kreative Projekte
Apr 02, 2025 pm 06:10 PM
Beste KI -Kunstgeneratoren (kostenlos & amp; bezahlt) für kreative Projekte
Apr 02, 2025 pm 06:10 PM
Der Artikel überprüft Top -KI -Kunstgeneratoren, diskutiert ihre Funktionen, Eignung für kreative Projekte und Wert. Es zeigt MidJourney als den besten Wert für Fachkräfte und empfiehlt Dall-E 2 für hochwertige, anpassbare Kunst.
 Ist Chatgpt 4 o verfügbar?
Mar 28, 2025 pm 05:29 PM
Ist Chatgpt 4 o verfügbar?
Mar 28, 2025 pm 05:29 PM
Chatgpt 4 ist derzeit verfügbar und weit verbreitet, wodurch im Vergleich zu seinen Vorgängern wie ChatGPT 3.5 signifikante Verbesserungen beim Verständnis des Kontextes und des Generierens kohärenter Antworten zeigt. Zukünftige Entwicklungen können mehr personalisierte Inters umfassen
 Welche KI ist besser als Chatgpt?
Mar 18, 2025 pm 06:05 PM
Welche KI ist besser als Chatgpt?
Mar 18, 2025 pm 06:05 PM
Der Artikel erörtert KI -Modelle, die Chatgpt wie Lamda, Lama und Grok übertreffen und ihre Vorteile in Bezug auf Genauigkeit, Verständnis und Branchenauswirkungen hervorheben. (159 Charaktere)
 So verwenden Sie Mistral OCR für Ihr nächstes Lappenmodell
Mar 21, 2025 am 11:11 AM
So verwenden Sie Mistral OCR für Ihr nächstes Lappenmodell
Mar 21, 2025 am 11:11 AM
Mistral OCR: revolutionäre retrieval-ausgereifte Generation mit multimodalem Dokumentverständnis RAG-Systeme (Abrufen-Augment-Augmented Generation) haben erheblich fortschrittliche KI
 Top -KI -Schreibassistenten, um Ihre Inhaltserstellung zu steigern
Apr 02, 2025 pm 06:11 PM
Top -KI -Schreibassistenten, um Ihre Inhaltserstellung zu steigern
Apr 02, 2025 pm 06:11 PM
In dem Artikel werden Top -KI -Schreibassistenten wie Grammarly, Jasper, Copy.ai, Writesonic und RYTR erläutert und sich auf ihre einzigartigen Funktionen für die Erstellung von Inhalten konzentrieren. Es wird argumentiert, dass Jasper in der SEO -Optimierung auszeichnet, während KI -Tools dazu beitragen, den Ton zu erhalten




