

Clustering oder Clusteranalyse ist ein unbeaufsichtigtes Lernproblem. Es wird häufig als Datenanalysetechnik eingesetzt, um interessante Muster in Daten zu entdecken, beispielsweise Kundensegmente anhand ihres Verhaltens. Es stehen viele Clustering-Algorithmen zur Auswahl, und es gibt keinen einzigen besten Clustering-Algorithmus für alle Situationen. Stattdessen ist es besser, eine Reihe von Clustering-Algorithmen und unterschiedliche Konfigurationen jedes Algorithmus zu untersuchen. In diesem Tutorial erfahren Sie, wie Sie die besten Clustering-Algorithmen in Python installieren und verwenden.
Nach Abschluss dieses Tutorials wissen Sie:
Tutorial-Übersicht
Clustering Die Analyse, also das Clustering, erfolgt unüberwacht Maschinelles Lernen. Es umfasst die automatische Erkennung natürlicher Gruppierungen in Daten. Im Gegensatz zum überwachten Lernen (ähnlich der prädiktiven Modellierung) interpretieren Clustering-Algorithmen einfach die Eingabedaten und finden natürliche Gruppen oder Cluster im Merkmalsraum.
Ein Cluster ist typischerweise ein Dichtebereich im Merkmalsraum, in dem Beispiele (Beobachtungen oder Datenzeilen) aus der Domäne näher am Cluster liegen als andere Cluster. Ein Cluster kann einen Mittelpunkt (Schwerpunkt) haben, der ein Muster- oder Punktmerkmalsraum ist, und kann Grenzen oder Bereiche haben.
Clustering kann als Datenanalyseaktivität hilfreich sein, um mehr über die Problemdomäne zu erfahren, die als Mustererkennung oder Wissenserkennung bezeichnet wird. Zum Beispiel:
Clustering kann auch als eine Art Feature-Engineering verwendet werden, bei dem bestehende und neue Beispiele zugeordnet und als zu einem der in den Daten identifizierten Cluster gehörend gekennzeichnet werden können. Zwar gibt es viele Cluster-spezifische quantitative Messungen, die Bewertung identifizierter Cluster ist jedoch subjektiv und erfordert möglicherweise Fachexperten. Typischerweise werden Clustering-Algorithmen wissenschaftlich anhand synthetischer Datensätze mit vordefinierten Clustern verglichen, die der Algorithmus voraussichtlich entdecken wird.
Es gibt viele Arten von Clustering-Algorithmen. Viele Algorithmen verwenden Ähnlichkeits- oder Abstandsmaße zwischen Beispielen im Merkmalsraum, um dichte Beobachtungsregionen zu entdecken. Daher empfiehlt es sich häufig, Ihre Daten zu erweitern, bevor Sie einen Clustering-Algorithmus verwenden.
Bei einigen Clustering-Algorithmen müssen Sie die Anzahl der in den Daten zu findenden Cluster angeben oder schätzen, während andere bestimmte Beobachtungen erfordern. Das Minimum Abstand, zwischen dem ein Beispiel als „geschlossen“ oder „verbunden“ betrachtet werden kann. Bei der Clusteranalyse handelt es sich daher um einen iterativen Prozess, bei dem subjektive Einschätzungen identifizierter Cluster in Änderungen in der Algorithmuskonfiguration zurückgeführt werden, bis gewünschte oder angemessene Ergebnisse erzielt werden. Die scikit-learn-Bibliothek bietet eine Reihe verschiedener Clustering-Algorithmen zur Auswahl. 10 der beliebtesten Algorithmen sind unten aufgeführt:
Jeder Algorithmus Beide bieten a unterschiedliche Herangehensweise an die Herausforderung, natürliche Gruppen in Daten zu entdecken. Es gibt keinen besten Clustering-Algorithmus und es gibt keine einfache Möglichkeit, den besten Algorithmus für Ihre Daten zu finden, ohne kontrollierte Experimente durchzuführen. In diesem Tutorial erfahren Sie, wie Sie jeden dieser 10 beliebten Clustering-Algorithmen aus der scikit-learn-Bibliothek verwenden. Diese Beispiele bieten Ihnen eine Grundlage zum Kopieren und Einfügen der Beispiele und zum Testen der Methoden an Ihren eigenen Daten. Wir werden uns nicht mit der Theorie befassen, wie Algorithmen funktionieren, noch werden wir sie direkt vergleichen. Lassen Sie uns etwas tiefer graben.
In diesem Abschnitt besprechen wir die Verwendung von 10 beliebten Clustering-Algorithmen in scikit-learn. Dazu gehören ein Beispiel für die Anpassung eines Modells und ein Beispiel für die Visualisierung der Ergebnisse. Diese Beispiele dienen zum Einfügen und Kopieren in Ihr eigenes Projekt und zum Anwenden der Methoden auf Ihre eigenen Daten.
Zunächst installieren wir die Bibliothek. Überspringen Sie diesen Schritt nicht, da Sie sicherstellen müssen, dass Sie die neueste Version installiert haben. Sie können das scikit-learn-Repository mit dem pip-Python-Installationsprogramm wie unten gezeigt installieren:
sudo pip install scikit-learn
Als Nächstes bestätigen wir, dass die Bibliothek installiert wurde und Sie eine moderne Version verwenden. Führen Sie das folgende Skript aus, um die Versionsnummer der Bibliothek auszugeben.
# 检查 scikit-learn 版本 import sklearn print(sklearn.__version__)
Wenn Sie das Beispiel ausführen, sollten Sie die folgende Versionsnummer oder höher sehen.
0.22.1
Wir werden die Funktion make_classification() verwenden, um einen Test-Binärklassifizierungsdatensatz zu erstellen. Der Datensatz wird 1000 Beispiele mit zwei Eingabefunktionen und einem Cluster pro Klasse enthalten. Diese Cluster sind in zwei Dimensionen sichtbar, sodass wir die Daten in einem Streudiagramm darstellen und die Punkte im Diagramm anhand des angegebenen Clusters einfärben können.
Dies hilft zu verstehen, wie gut die Cluster identifiziert werden, zumindest beim Testproblem. Die Cluster in diesem Testproblem basieren auf multivariaten Gaußschen Gleichungen, und nicht alle Clustering-Algorithmen sind bei der Identifizierung dieser Clustertypen effektiv. Daher sollten die Ergebnisse in diesem Tutorial nicht als Grundlage für den Vergleich allgemeiner Methoden verwendet werden. Nachfolgend sind Beispiele für die Erstellung und Zusammenfassung synthetischer Clustering-Datensätze aufgeführt.
# 综合分类数据集 from numpy import where from sklearn.datasets import make_classification from matplotlib import pyplot # 定义数据集 X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 为每个类的样本创建散点图 for class_value in range(2): # 获取此类的示例的行索引 row_ix = where(y == class_value) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
Durch die Ausführung dieses Beispiels wird ein synthetischer geclusterter Datensatz erstellt und anschließend ein Streudiagramm der Eingabedaten mit Punkten, die durch Klassenbezeichnungen (idealisierte Cluster) gefärbt sind. Wir können deutlich zwei verschiedene Datengruppen in zwei Dimensionen erkennen und hoffen, dass ein automatischer Clustering-Algorithmus diese Gruppierungen erkennen kann.
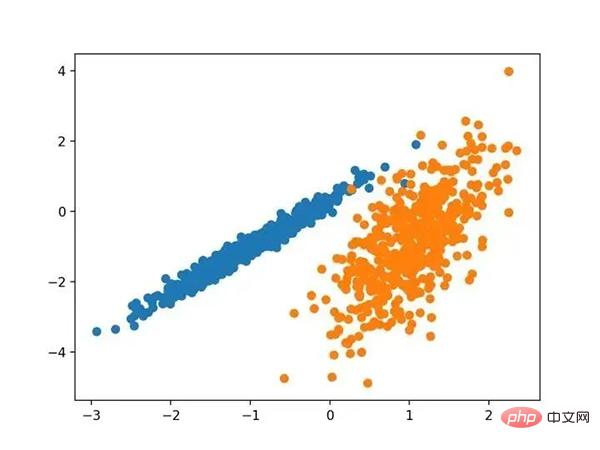
Streudiagramm eines synthetischen Cluster-Datensatzes bekannter Cluster-Farbpunkte
Als nächstes können wir uns Beispiele für Clustering-Algorithmen ansehen, die auf diesen Datensatz angewendet werden. Ich habe einige minimale Versuche unternommen, jede Methode an den Datensatz anzupassen.
Bei der Affinitätsausbreitung geht es darum, eine Reihe von Exemplaren zu finden, die die Daten am besten zusammenfassen.
Es wird durch die AffinityPropagation-Klasse implementiert. Die Hauptkonfiguration, die angepasst werden muss, besteht darin, die „Dämpfung“ von 0,5 auf 1 festzulegen, möglicherweise sogar die „Einstellungen“.
Vollständige Beispiele unten aufgeführt.
# 亲和力传播聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AffinityPropagation from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = AffinityPropagation(damping=0.9) # 匹配模型 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
Führen Sie das Beispiel aus, um das Modell an den Trainingsdatensatz anzupassen und den Cluster für jedes Beispiel im Datensatz vorherzusagen. Anschließend wird ein Streudiagramm erstellt, das nach den zugewiesenen Clustern gefärbt ist. In diesem Fall kann ich keine guten Ergebnisse erzielen.
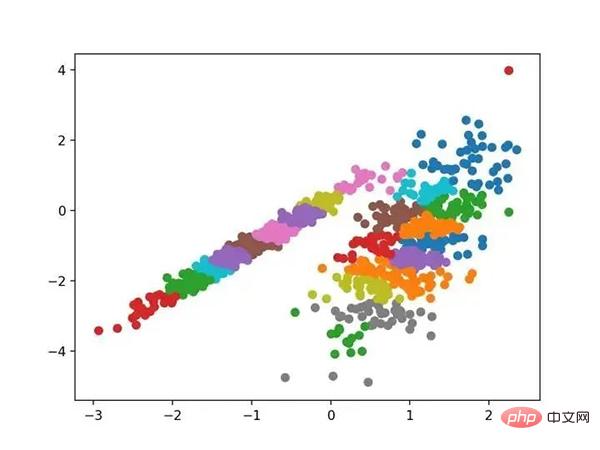
Streudiagramm eines Datensatzes mit Clustern, die mithilfe der Affinitätsausbreitung identifiziert wurden
Beim aggregierten Clustering werden Beispiele zusammengeführt, bis die gewünschte Anzahl von Clustern erreicht ist. Es ist Teil einer breiteren Klasse hierarchischer Clustering-Methoden, die durch die Klasse AgglomerationClustering implementiert werden, und die Hauptkonfiguration ist der Satz „n_clusters“, der eine Schätzung der Anzahl der Cluster in den Daten darstellt, z. B. 2. Ein vollständiges Beispiel ist unten aufgeführt.
# 聚合聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AgglomerativeClustering from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = AgglomerativeClustering(n_clusters=2) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
Führen Sie das Beispiel aus, um das Modell an den Trainingsdatensatz anzupassen und den Cluster für jedes Beispiel im Datensatz vorherzusagen. Anschließend wird ein Streudiagramm erstellt, das nach den zugewiesenen Clustern gefärbt ist. In diesem Fall kann eine sinnvolle Gruppierung gefunden werden.
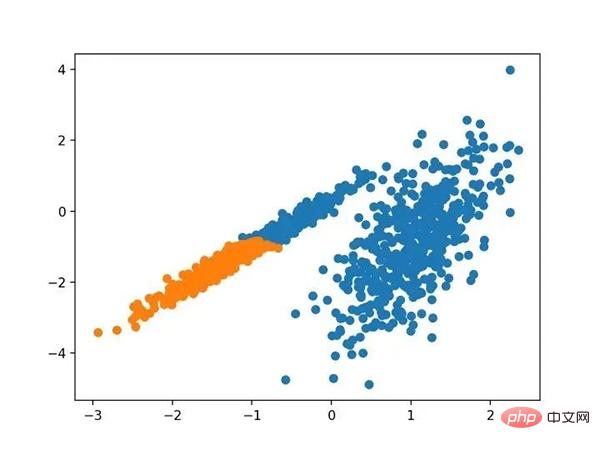
Streudiagramm eines Datensatzes mit Clustern, die mithilfe agglomerativer Clusterbildung identifiziert wurden
BIRCH 聚类( BIRCH 是平衡迭代减少的缩写,聚类使用层次结构)包括构造一个树状结构,从中提取聚类质心。
它是通过 Birch 类实现的,主要配置是“ threshold ”和“ n _ clusters ”超参数,后者提供了群集数量的估计。下面列出了完整的示例。
# birch聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import Birch from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = Birch(threshold=0.01, n_clusters=2) # 适配模型 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以找到一个很好的分组。
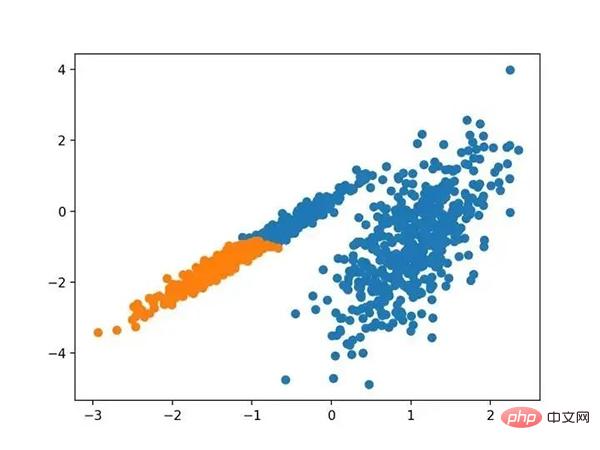
使用BIRCH聚类确定具有聚类的数据集的散点图
DBSCAN 聚类(其中 DBSCAN 是基于密度的空间聚类的噪声应用程序)涉及在域中寻找高密度区域,并将其周围的特征空间区域扩展为群集。
它是通过 DBSCAN 类实现的,主要配置是“ eps ”和“ min _ samples ”超参数。
下面列出了完整的示例。
# dbscan 聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import DBSCAN from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = DBSCAN(eps=0.30, min_samples=9) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,尽管需要更多的调整,但是找到了合理的分组。
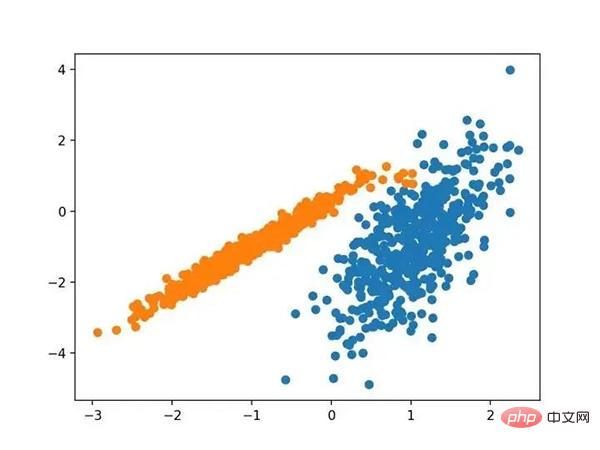
使用DBSCAN集群识别出具有集群的数据集的散点图
K-均值聚类可以是最常见的聚类算法,并涉及向群集分配示例,以尽量减少每个群集内的方差。
它是通过 K-均值类实现的,要优化的主要配置是“ n _ clusters ”超参数设置为数据中估计的群集数量。下面列出了完整的示例。
# k-means 聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import KMeans from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = KMeans(n_clusters=2) # 模型拟合 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以找到一个合理的分组,尽管每个维度中的不等等方差使得该方法不太适合该数据集。
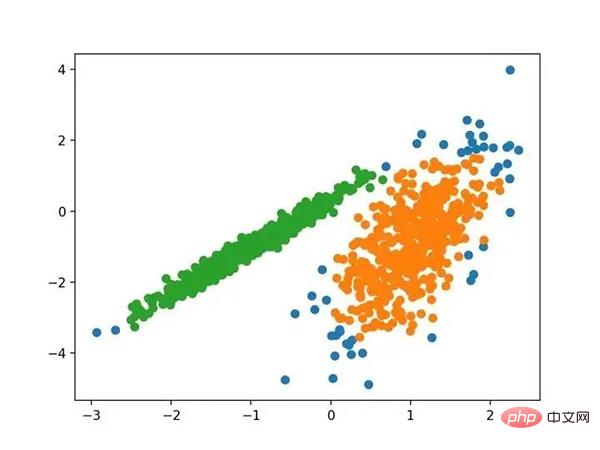
使用K均值聚类识别出具有聚类的数据集的散点图
Mini-Batch K-均值是 K-均值的修改版本,它使用小批量的样本而不是整个数据集对群集质心进行更新,这可以使大数据集的更新速度更快,并且可能对统计噪声更健壮。
它是通过 MiniBatchKMeans 类实现的,要优化的主配置是“ n _ clusters ”超参数,设置为数据中估计的群集数量。下面列出了完整的示例。
# mini-batch k均值聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MiniBatchKMeans from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = MiniBatchKMeans(n_clusters=2) # 模型拟合 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,会找到与标准 K-均值算法相当的结果。
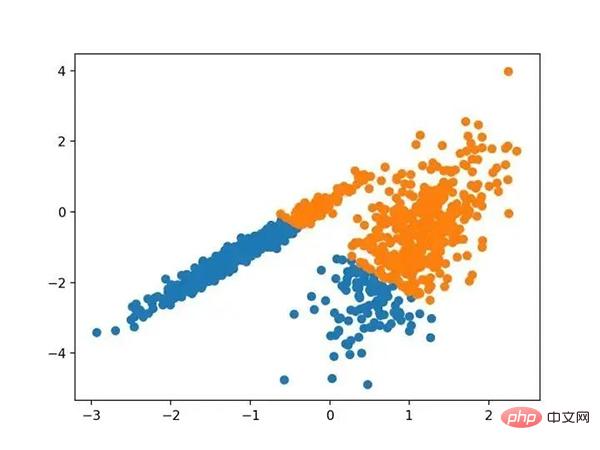
带有最小批次K均值聚类的聚类数据集的散点图
均值漂移聚类涉及到根据特征空间中的实例密度来寻找和调整质心。
它是通过 MeanShift 类实现的,主要配置是“带宽”超参数。下面列出了完整的示例。
# 均值漂移聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MeanShift from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = MeanShift() # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以在数据中找到一组合理的群集。
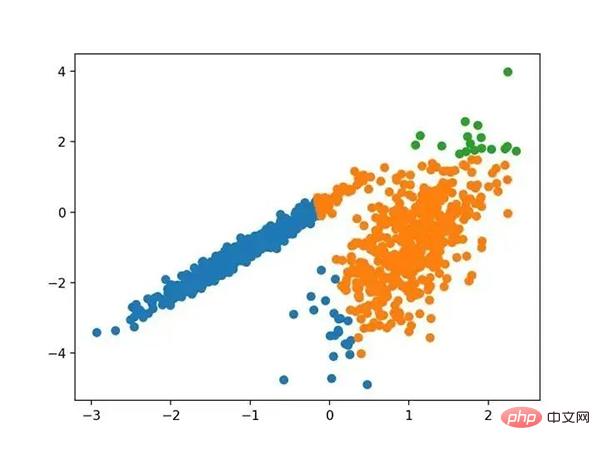
具有均值漂移聚类的聚类数据集散点图
OPTICS 聚类( OPTICS 短于订购点数以标识聚类结构)是上述 DBSCAN 的修改版本。
它是通过 OPTICS 类实现的,主要配置是“ eps ”和“ min _ samples ”超参数。下面列出了完整的示例。
# optics聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import OPTICS from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = OPTICS(eps=0.8, min_samples=10) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,我无法在此数据集上获得合理的结果。
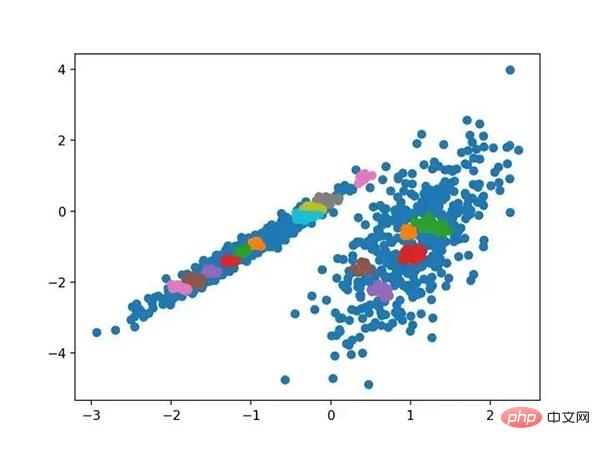
使用OPTICS聚类确定具有聚类的数据集的散点图
光谱聚类是一类通用的聚类方法,取自线性线性代数。
它是通过 Spectral 聚类类实现的,而主要的 Spectral 聚类是一个由聚类方法组成的通用类,取自线性线性代数。要优化的是“ n _ clusters ”超参数,用于指定数据中的估计群集数量。下面列出了完整的示例。
# spectral clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import SpectralClustering from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = SpectralClustering(n_clusters=2) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。
在这种情况下,找到了合理的集群。
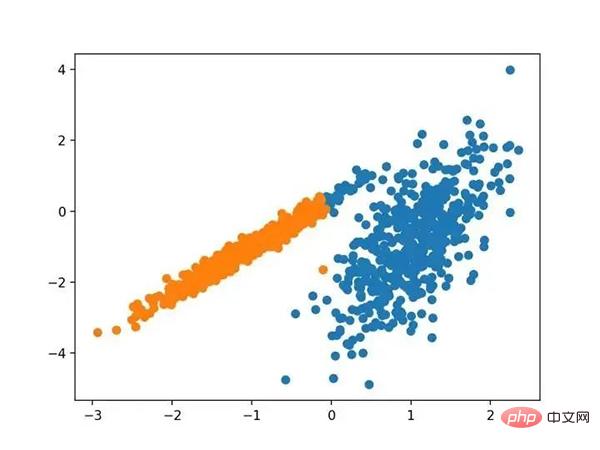
使用光谱聚类聚类识别出具有聚类的数据集的散点图
高斯混合模型总结了一个多变量概率密度函数,顾名思义就是混合了高斯概率分布。它是通过 Gaussian Mixture 类实现的,要优化的主要配置是“ n _ clusters ”超参数,用于指定数据中估计的群集数量。下面列出了完整的示例。
# 高斯混合模型 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.mixture import GaussianMixture from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = GaussianMixture(n_components=2) # 模型拟合 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,我们可以看到群集被完美地识别。这并不奇怪,因为数据集是作为 Gaussian 的混合生成的。
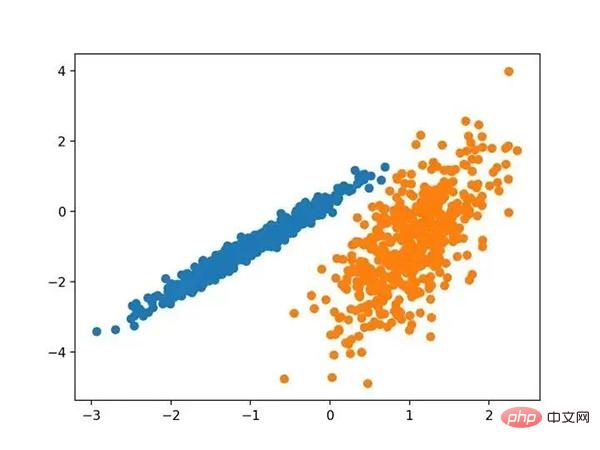
使用高斯混合聚类识别出具有聚类的数据集的散点图
在本教程中,您发现了如何在 python 中安装和使用顶级聚类算法。具体来说,你学到了:
Das obige ist der detaillierte Inhalt vonVollständige Python-Betriebsbeispiele für zehn Clustering-Algorithmen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




