 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 Grundlagen des maschinellen Lernens: Wie kann eine Überanpassung verhindert werden?
Grundlagen des maschinellen Lernens: Wie kann eine Überanpassung verhindert werden?
Grundlagen des maschinellen Lernens: Wie kann eine Überanpassung verhindert werden?
Tatsächlich ist das Wesen der Regularisierung sehr einfach. Es handelt sich um ein Mittel oder eine Operation, die einem bestimmten Problem a priori Einschränkungen oder Einschränkungen auferlegt, um einen bestimmten Zweck zu erreichen. Der Zweck der Verwendung der Regularisierung in einem Algorithmus besteht darin, eine Überanpassung des Modells zu verhindern. Wenn es um die Regularisierung geht, denken viele Schüler möglicherweise sofort an die häufig verwendete L1-Norm und die L2-Norm. Bevor wir zusammenfassen, werfen wir zunächst einen Blick auf die LP-Norm.
LP-Norm
Norm kann einfach so verstanden werden, dass sie zur Darstellung des Abstands im Vektorraum verwendet wird, und die Definition des Abstands ist sehr abstrakt, solange sie nicht negativ erfüllt, reflexiv und trigonometrisch Die Ungleichung kann als Distanz bezeichnet werden.
LP-Norm ist keine Norm, sondern eine Reihe von Normen, die wie folgt definiert ist:
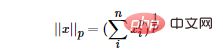
Der Bereich von p ist [1,∞). p ist im Bereich von (0,1) nicht als Norm definiert, da es die Dreiecksungleichung verletzt.
Entsprechend der Änderung von pp weist die Norm auch unterschiedliche Änderungen auf. Ein klassisches Änderungsdiagramm der P-Norm wie folgt:

Dann stellt sich die Frage: Was ist die L0-Norm? Die L0-Norm stellt die Anzahl der Nicht-Null-Elemente im Vektor dar und wird wie folgt ausgedrückt:
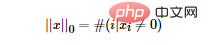
#🎜 🎜# Wie Sie der obigen Formel entnehmen können, ist die L1-Norm die Summe der Absolutwerte jedes Elements des Vektors, auch bekannt als „Sparse-Regeloperator“ (Lasso-Regularisierung). Die Frage ist also: Warum wollen wir eine Sparsifizierung? Die Sparsifizierung hat viele Vorteile, die beiden direktesten sind:
Wie Sie der obigen Formel entnehmen können, ist die L1-Norm die Summe der Absolutwerte jedes Elements des Vektors, auch bekannt als „Sparse-Regeloperator“ (Lasso-Regularisierung). Die Frage ist also: Warum wollen wir eine Sparsifizierung? Die Sparsifizierung hat viele Vorteile, die beiden direktesten sind:
- Interpretierbarkeit
- L2 Die Norm
Die L2-Norm ist die euklidische Distanz. Die Formel lautet wie folgt:
Die L2-Norm hat viele Namen. Manche nennen ihre Regression „Ridge-Regression“, während andere sie „Weight Decay“ nennen. Durch die Verwendung der L2-Norm als Regularisierungsterm kann eine dichte Lösung erhalten werden, d Die Berücksichtigung des Trainingssatzes führt zu einer Überanpassung und verbessert dadurch die Generalisierungsfähigkeit des Modells. 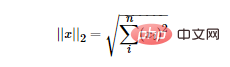

Aus bayesianischer Sicht reicht es beim Training eines Modells nicht aus, sich ausschließlich auf den aktuellen Trainingsdatensatz zu verlassen. Um bessere Generalisierungsfähigkeiten zu erreichen, ist es häufig erforderlich, vorherige Terme hinzuzufügen, und das Hinzufügen regulärer Terme ist gleichbedeutend mit A priori wurde hinzugefügt.
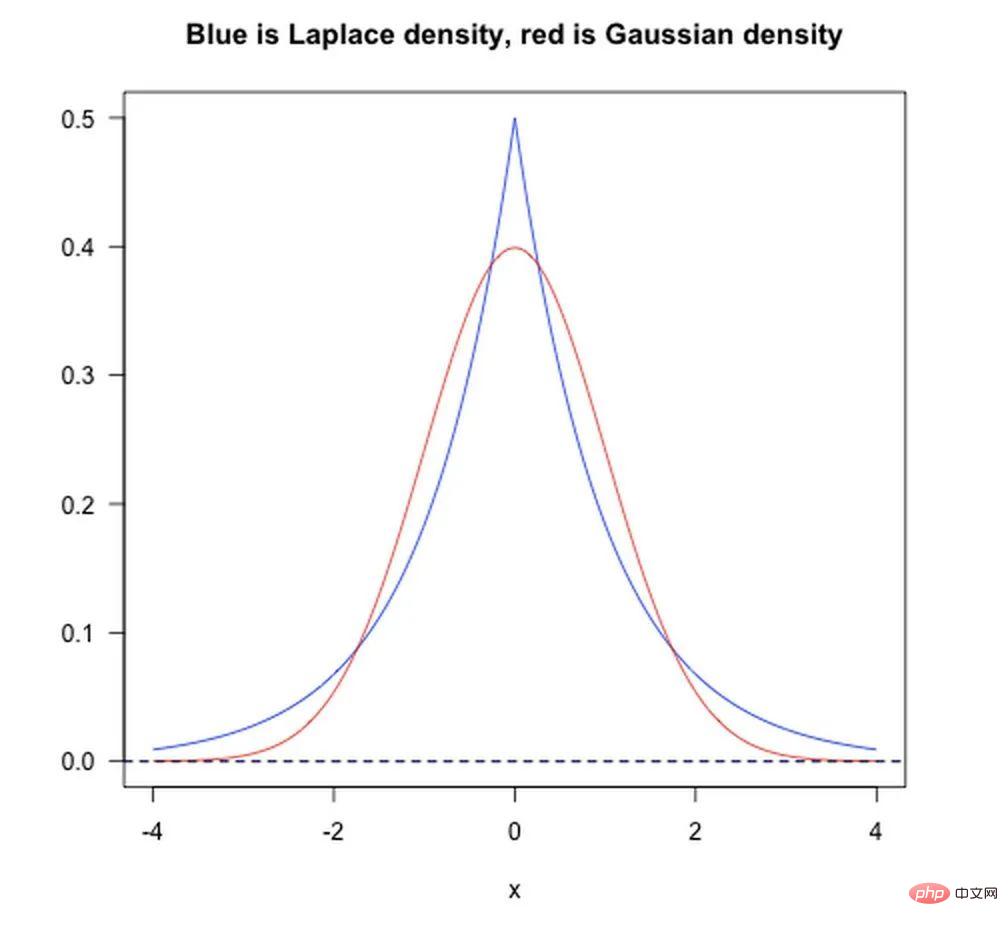
- L1-Norm entspricht dem Hinzufügen eines Laplaceschen Priors.
- L2-Norm entspricht dem Hinzufügen eines Gaußschen Priors.
Wie in der folgenden Abbildung gezeigt:
Dropout
Dropout ist eine Regularisierungsmethode, die häufig beim Deep Learning verwendet wird. Sein Ansatz kann einfach so verstanden werden, dass während des Trainingsprozesses von DNNs einige Neuronen mit der Wahrscheinlichkeit p verworfen werden, was bedeutet, dass die Ausgabe der verworfenen Neuronen 0 ist. Dropout kann wie in der folgenden Abbildung gezeigt instanziiert werden:
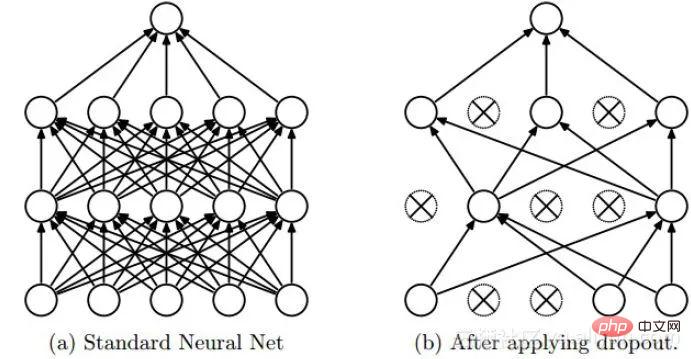
Wir können den Regularisierungseffekt von Dropout aus zwei Aspekten intuitiv verstehen:
- Der Vorgang des zufälligen Verlusts von Neuronen während jeder Runde des Dropout-Trainings entspricht mehreren DNNs gemittelt, so dass sie den Effekt einer Abstimmung haben, wenn sie zur Vorhersage verwendet werden.
- Reduzieren Sie die komplexe Koadaption zwischen Neuronen. Wenn die Neuronen der verborgenen Schicht zufällig gelöscht werden, wird das vollständig verbundene Netzwerk bis zu einem gewissen Grad spärlich, wodurch die Synergieeffekte verschiedener Funktionen effektiv verringert werden. Mit anderen Worten: Einige Funktionen basieren möglicherweise auf der gemeinsamen Aktion versteckter Knoten mit festen Beziehungen. Durch Dropout wird die Situation effektiv organisiert, in der einige Funktionen nur in Gegenwart anderer Funktionen wirksam sind, wodurch die Robustheit des neuronalen Netzwerks erheblich erhöht wird Sex.
Batch-Normalisierung
Batch-Normalisierung ist eine reine Normalisierungsmethode, die hauptsächlich zur Beschleunigung der Konvergenz des Netzwerks verwendet wird, aber auch einen gewissen Regularisierungseffekt hat.
Hier ist ein Verweis auf die Erklärung der Kovariatenverschiebung in der Zhihu-Antwort von Dr. Wei Xushen.
Hinweis: Der folgende Inhalt stammt aus der Zhihu-Antwort von Dr. ist konsistent“. Wenn sie inkonsistent sind, entstehen neue Probleme beim maschinellen Lernen, wie z. B. Transferlernen/Domänenanpassung usw. Die Kovariatenverschiebung ist ein Zweigproblem unter der Annahme einer inkonsistenten Verteilung. Dies bedeutet, dass die bedingten Wahrscheinlichkeiten des Quellraums und des Zielraums konsistent sind, ihre Grenzwahrscheinlichkeiten jedoch unterschiedlich sind. Wenn Sie sorgfältig darüber nachdenken, werden Sie feststellen, dass sich die Verteilung der Ausgabe jeder Schicht des neuronalen Netzwerks offensichtlich von der Verteilung der jeder Schicht entsprechenden Eingangssignale unterscheidet, da sie Operationen innerhalb der Schicht durchlaufen haben. und der Unterschied wird mit zunehmender Tiefe des Netzwerks größer, aber die Stichprobenbezeichnungen, die sie „angeben“ können, bleiben unverändert, was der Definition der Kovariatenverschiebung entspricht.
Die Grundidee von BN ist eigentlich recht intuitiv, da sich der Aktivierungseingabewert des neuronalen Netzwerks vor der nichtlinearen Transformation (X = WU + B, U ist die Eingabe) mit zunehmender Tiefe des Netzwerks allmählich verschiebt oder Änderungen (d. h. die oben erwähnte Kovariatenverschiebung). Der Grund für die langsame Konvergenz des Trainings liegt im Allgemeinen darin, dass sich die Gesamtverteilung allmählich der Ober- und Untergrenze des Wertebereichs der nichtlinearen Funktion nähert (für die Sigmoidfunktion bedeutet dies, dass der Aktivierungseingabewert X = WU + B ein großer negativer oder negativer Wert ist). positiver Wert ), was dazu führt, dass der Gradient des neuronalen Netzwerks auf niedriger Ebene während der Backpropagation verschwindet, was der wesentliche Grund dafür ist, dass das Training tiefer neuronaler Netzwerke immer langsamer konvergiert. BN verwendet eine bestimmte Standardisierungsmethode, um die Verteilung des Eingabewerts eines beliebigen Neurons in jeder Schicht des neuronalen Netzwerks mit einem Mittelwert von 0 und einer Varianz von 1 auf die Standardnormalverteilung zurückzusetzen, um das dadurch verursachte Problem der Gradientendispersion zu vermeiden Aktivierungsfunktion. Anstatt also zu sagen, dass die Rolle von BN darin besteht, Kovariatenverschiebungen zu mildern, ist es besser zu sagen, dass BN das Problem der Gradientendispersion lindern kann.
Normalisierung, Standardisierung und Regularisierung
Wir haben die Regularisierung bereits erwähnt, hier erwähnen wir kurz die Normalisierung und Standardisierung. Normalisierung: Das Ziel der Normalisierung besteht darin, eine bestimmte Zuordnungsbeziehung zu finden, um die Originaldaten dem Intervall [a, b] zuzuordnen. Im Allgemeinen nehmen a und b Kombinationen von [−1,1], [0,1] an. Im Allgemeinen gibt es zwei Anwendungsszenarien:
- Konvertieren Sie die Zahl in eine Dezimalzahl zwischen (0, 1)
- Konvertieren Sie die Dimensionszahl in eine dimensionslose Zahl.
Häufig verwendete Min-Max-Normalisierung:
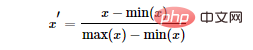
Standardisierung: Verwendung der Satz großer Zahlen zur Umwandlung der Daten in eine Standardnormalverteilung. Die Standardisierungsformel lautet:

Der Unterschied zwischen Normalisierung und Standardisierung:
Wir können es einfach so erklären: Die normalisierte Skalierung wird gleichmäßig auf das Intervall (nur durch Extremwerte bestimmt) „abgeflacht“, während die normalisierte Skalierung „elastischer“ und „dynamischer“ ist hat einen guten Zusammenhang mit der Verteilung der Gesamtstichprobe. Hinweis:
- Normalisierung: Die Skalierung bezieht sich nur auf die Differenz zwischen den Maximal- und Minimalwerten.
- Standardisierung: Die Skalierung bezieht sich auf jeden Punkt und spiegelt sich in der Varianz wider. Vergleichen Sie dies mit der Normalisierung, bei der alle Datenpunkte einen Beitrag leisten (über den Mittelwert und die Standardabweichung).
Warum Standardisierung und Normalisierung?
- Modellgenauigkeit verbessern: Nach der Normalisierung sind die Merkmale zwischen verschiedenen Dimensionen numerisch vergleichbar, was die Genauigkeit des Klassifikators erheblich verbessern kann.
- Modellkonvergenz beschleunigen: Nach der Standardisierung wird der Optimierungsprozess der optimalen Lösung offensichtlich reibungsloser, was die korrekte Konvergenz zur optimalen Lösung erleichtert. Wie im Bild unten gezeigt:
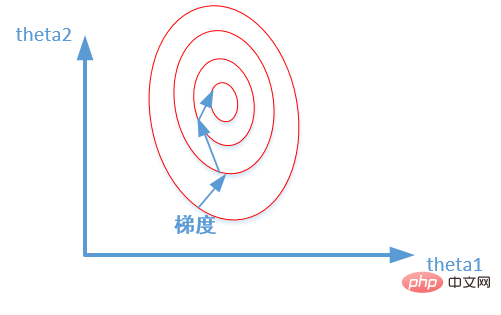
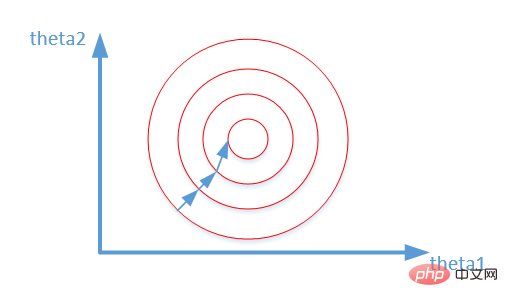
Das obige ist der detaillierte Inhalt vonGrundlagen des maschinellen Lernens: Wie kann eine Überanpassung verhindert werden?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In diesem Artikel erfahren Sie mehr über SHAP: Modellerklärung für maschinelles Lernen
Jun 01, 2024 am 10:58 AM
In den Bereichen maschinelles Lernen und Datenwissenschaft stand die Interpretierbarkeit von Modellen schon immer im Fokus von Forschern und Praktikern. Mit der weit verbreiteten Anwendung komplexer Modelle wie Deep Learning und Ensemble-Methoden ist das Verständnis des Entscheidungsprozesses des Modells besonders wichtig geworden. Explainable AI|XAI trägt dazu bei, Vertrauen in maschinelle Lernmodelle aufzubauen, indem es die Transparenz des Modells erhöht. Eine Verbesserung der Modelltransparenz kann durch Methoden wie den weit verbreiteten Einsatz mehrerer komplexer Modelle sowie der Entscheidungsprozesse zur Erläuterung der Modelle erreicht werden. Zu diesen Methoden gehören die Analyse der Merkmalsbedeutung, die Schätzung des Modellvorhersageintervalls, lokale Interpretierbarkeitsalgorithmen usw. Die Merkmalswichtigkeitsanalyse kann den Entscheidungsprozess des Modells erklären, indem sie den Grad des Einflusses des Modells auf die Eingabemerkmale bewertet. Schätzung des Modellvorhersageintervalls
 Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Jenseits von ORB-SLAM3! SL-SLAM: Szenen mit wenig Licht, starkem Jitter und schwacher Textur werden verarbeitet
May 30, 2024 am 09:35 AM
Heute diskutieren wir darüber, wie Deep-Learning-Technologie die Leistung von visionbasiertem SLAM (Simultaneous Localization and Mapping) in komplexen Umgebungen verbessern kann. Durch die Kombination von Methoden zur Tiefenmerkmalsextraktion und Tiefenanpassung stellen wir hier ein vielseitiges hybrides visuelles SLAM-System vor, das die Anpassung in anspruchsvollen Szenarien wie schlechten Lichtverhältnissen, dynamischer Beleuchtung, schwach strukturierten Bereichen und starkem Jitter verbessern soll. Unser System unterstützt mehrere Modi, einschließlich erweiterter Monokular-, Stereo-, Monokular-Trägheits- und Stereo-Trägheitskonfigurationen. Darüber hinaus wird analysiert, wie visuelles SLAM mit Deep-Learning-Methoden kombiniert werden kann, um andere Forschungen zu inspirieren. Durch umfangreiche Experimente mit öffentlichen Datensätzen und selbst abgetasteten Daten demonstrieren wir die Überlegenheit von SL-SLAM in Bezug auf Positionierungsgenauigkeit und Tracking-Robustheit.
 Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Zu den häufigsten Herausforderungen, mit denen Algorithmen für maschinelles Lernen in C++ konfrontiert sind, gehören Speicherverwaltung, Multithreading, Leistungsoptimierung und Wartbarkeit. Zu den Lösungen gehören die Verwendung intelligenter Zeiger, moderner Threading-Bibliotheken, SIMD-Anweisungen und Bibliotheken von Drittanbietern sowie die Einhaltung von Codierungsstilrichtlinien und die Verwendung von Automatisierungstools. Praktische Fälle zeigen, wie man die Eigen-Bibliothek nutzt, um lineare Regressionsalgorithmen zu implementieren, den Speicher effektiv zu verwalten und leistungsstarke Matrixoperationen zu nutzen.
 Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Erklärbare KI: Erklären komplexer KI/ML-Modelle
Jun 03, 2024 pm 10:08 PM
Übersetzer |. Rezensiert von Li Rui |. Chonglou Modelle für künstliche Intelligenz (KI) und maschinelles Lernen (ML) werden heutzutage immer komplexer, und die von diesen Modellen erzeugten Ergebnisse sind eine Blackbox, die den Stakeholdern nicht erklärt werden kann. Explainable AI (XAI) zielt darauf ab, dieses Problem zu lösen, indem es Stakeholdern ermöglicht, die Funktionsweise dieser Modelle zu verstehen, sicherzustellen, dass sie verstehen, wie diese Modelle tatsächlich Entscheidungen treffen, und Transparenz in KI-Systemen, Vertrauen und Verantwortlichkeit zur Lösung dieses Problems gewährleistet. In diesem Artikel werden verschiedene Techniken der erklärbaren künstlichen Intelligenz (XAI) untersucht, um ihre zugrunde liegenden Prinzipien zu veranschaulichen. Mehrere Gründe, warum erklärbare KI von entscheidender Bedeutung ist. Vertrauen und Transparenz: Damit KI-Systeme allgemein akzeptiert und vertrauenswürdig sind, müssen Benutzer verstehen, wie Entscheidungen getroffen werden
 Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Fünf Schulen des maschinellen Lernens, die Sie nicht kennen
Jun 05, 2024 pm 08:51 PM
Maschinelles Lernen ist ein wichtiger Zweig der künstlichen Intelligenz, der Computern die Möglichkeit gibt, aus Daten zu lernen und ihre Fähigkeiten zu verbessern, ohne explizit programmiert zu werden. Maschinelles Lernen hat ein breites Anwendungsspektrum in verschiedenen Bereichen, von der Bilderkennung und der Verarbeitung natürlicher Sprache bis hin zu Empfehlungssystemen und Betrugserkennung, und es verändert unsere Lebensweise. Im Bereich des maschinellen Lernens gibt es viele verschiedene Methoden und Theorien, von denen die fünf einflussreichsten Methoden als „Fünf Schulen des maschinellen Lernens“ bezeichnet werden. Die fünf Hauptschulen sind die symbolische Schule, die konnektionistische Schule, die evolutionäre Schule, die Bayes'sche Schule und die Analogieschule. 1. Der Symbolismus, auch Symbolismus genannt, betont die Verwendung von Symbolen zum logischen Denken und zum Ausdruck von Wissen. Diese Denkrichtung glaubt, dass Lernen ein Prozess der umgekehrten Schlussfolgerung durch das Vorhandene ist
 Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
01Ausblicksübersicht Derzeit ist es schwierig, ein angemessenes Gleichgewicht zwischen Detektionseffizienz und Detektionsergebnissen zu erreichen. Wir haben einen verbesserten YOLOv5-Algorithmus zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern entwickelt, der mehrschichtige Merkmalspyramiden, Multierkennungskopfstrategien und hybride Aufmerksamkeitsmodule verwendet, um die Wirkung des Zielerkennungsnetzwerks in optischen Fernerkundungsbildern zu verbessern. Laut SIMD-Datensatz ist der mAP des neuen Algorithmus 2,2 % besser als YOLOv5 und 8,48 % besser als YOLOX, wodurch ein besseres Gleichgewicht zwischen Erkennungsergebnissen und Geschwindigkeit erreicht wird. 02 Hintergrund und Motivation Mit der rasanten Entwicklung der Fernerkundungstechnologie wurden hochauflösende optische Fernerkundungsbilder verwendet, um viele Objekte auf der Erdoberfläche zu beschreiben, darunter Flugzeuge, Autos, Gebäude usw. Objekterkennung bei der Interpretation von Fernerkundungsbildern
 Ist Flash Attention stabil? Meta und Harvard stellten fest, dass die Gewichtsabweichungen ihrer Modelle um Größenordnungen schwankten
May 30, 2024 pm 01:24 PM
Ist Flash Attention stabil? Meta und Harvard stellten fest, dass die Gewichtsabweichungen ihrer Modelle um Größenordnungen schwankten
May 30, 2024 pm 01:24 PM
MetaFAIR hat sich mit Harvard zusammengetan, um einen neuen Forschungsrahmen zur Optimierung der Datenverzerrung bereitzustellen, die bei der Durchführung groß angelegten maschinellen Lernens entsteht. Es ist bekannt, dass das Training großer Sprachmodelle oft Monate dauert und Hunderte oder sogar Tausende von GPUs verwendet. Am Beispiel des Modells LLaMA270B erfordert das Training insgesamt 1.720.320 GPU-Stunden. Das Training großer Modelle stellt aufgrund des Umfangs und der Komplexität dieser Arbeitsbelastungen einzigartige systemische Herausforderungen dar. In letzter Zeit haben viele Institutionen über Instabilität im Trainingsprozess beim Training generativer SOTA-KI-Modelle berichtet. Diese treten normalerweise in Form von Verlustspitzen auf. Beim PaLM-Modell von Google kam es beispielsweise während des Trainingsprozesses zu Instabilitäten. Numerische Voreingenommenheit ist die Hauptursache für diese Trainingsungenauigkeit.
 AlphaFold 3 wird auf den Markt gebracht und sagt die Wechselwirkungen und Strukturen von Proteinen und allen Lebensmolekülen umfassend und mit weitaus größerer Genauigkeit als je zuvor voraus
Jul 16, 2024 am 12:08 AM
AlphaFold 3 wird auf den Markt gebracht und sagt die Wechselwirkungen und Strukturen von Proteinen und allen Lebensmolekülen umfassend und mit weitaus größerer Genauigkeit als je zuvor voraus
Jul 16, 2024 am 12:08 AM
Herausgeber | Rettichhaut Seit der Veröffentlichung des leistungsstarken AlphaFold2 im Jahr 2021 verwenden Wissenschaftler Modelle zur Proteinstrukturvorhersage, um verschiedene Proteinstrukturen innerhalb von Zellen zu kartieren, Medikamente zu entdecken und eine „kosmische Karte“ jeder bekannten Proteininteraktion zu zeichnen. Gerade hat Google DeepMind das AlphaFold3-Modell veröffentlicht, das gemeinsame Strukturvorhersagen für Komplexe wie Proteine, Nukleinsäuren, kleine Moleküle, Ionen und modifizierte Reste durchführen kann. Die Genauigkeit von AlphaFold3 wurde im Vergleich zu vielen dedizierten Tools in der Vergangenheit (Protein-Ligand-Interaktion, Protein-Nukleinsäure-Interaktion, Antikörper-Antigen-Vorhersage) deutlich verbessert. Dies zeigt, dass dies innerhalb eines einzigen einheitlichen Deep-Learning-Frameworks möglich ist



