Verwenden Sie Python, um die RSA-Verschlüsselung und -Entschlüsselung zu implementieren

Ich habe gestern einen englischen Artikel gesehen [1], der zeigt, wie man Python zur Implementierung des RSA-Algorithmus verwendet. Die Logik des Codes ist dieselbe wie im vorherigen Artikel. Freunde, die mit RSA nicht vertraut sind, können den Artikel lesen Den RSA-Algorithmus verstehen, der erklärt, was RSA ist, die mathematischen Prinzipien von RSA und ein einfaches Beispiel. Man kann sagen, dass es sich um den einfachsten Artikel zum Verständnis von RSA auf Quanzhihu handelt (dies stammt aus den Kommentaren der Leser).

Ich habe den auf Englisch bereitgestellten Code ausgeführt und festgestellt, dass Chinesisch nicht verschlüsselt werden konnte. Daher habe ich die Verschlüsselungs- und Entschlüsselungsfunktionen geändert, um die chinesische Verschlüsselung und Entschlüsselung zu unterstützen. Im heutigen Artikel erfahren Sie, wie Sie mit Python den RSA-Verschlüsselungs- und -Entschlüsselungsprozess implementieren, um ein intuitives Verständnis von RSA zu erlangen. Es lohnt sich auch, den Algorithmus zur Erzeugung zufälliger Primzahlen im Code zu erlernen.

0. Wirkungsdemonstration

Werfen wir zunächst einen Blick auf die Wirkung.

Originaltext: „Da ist ein Maulwurf, beenden Sie die Transaktion“

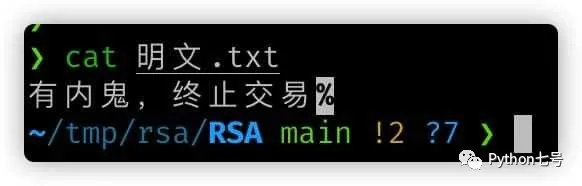
Der Chiffretext kann überhaupt nicht geknackt werden:

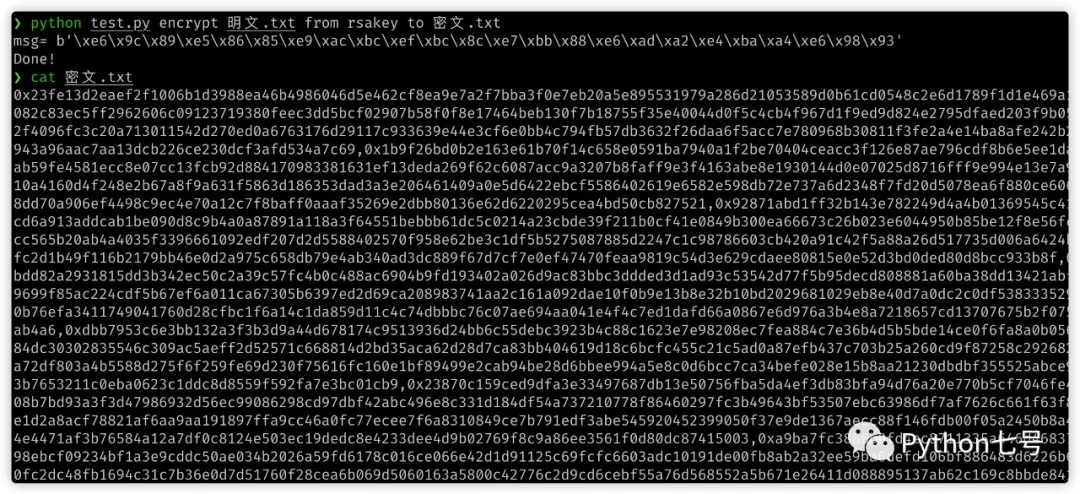
Nach der Entschlüsselung:

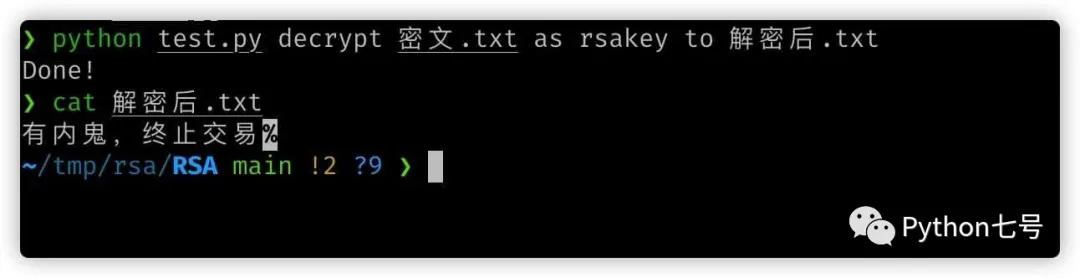
Öffentliches Konto mit vollständigem Code „Python Seven“ antwortete „rsa“ Get.

1. Schlüsselpaargenerierung

Ideen:

1) Finden Sie zufällig zwei Primzahlen (Primzahlen) p und q. Hier wählen wir eine 1024-Bit-Primzahl.

p = genprime(1024)
q = genprime(1024)

genprime( ) Reden wir nicht über den Implementierungsprozess der Funktion.

2) Berechnen Sie ihr Produkt n = p * q und die Euler-Funktion lambda_n.

n = p * q
lambda_n = (p - 1) * (q - 1)

3) Wählen Sie zufällig eine ganze Zahl e aus, vorausgesetzt, dass 1 < e < lambda_n und e und lambda_n relativ teilerfremd sind. Wenn Sie beispielsweise 35537 auswählen, hat 35537 nur 16 Bit und muss kleiner als lambda_n sein. < e < lambda_n，且 e 与 lambda_n 互质。比如选择 35537，35537 只有 16 位，必然小于 lambda_n。

e = 35537

4) Finden Sie eine Ganzzahl d, bei der der Rest von e * d dividiert durch lambda_n 1 ist, und geben Sie das Schlüsselpaar zurück.

d = eucalg(e, lambda_n)[0]
if d < 0: d += lambda_n
return (d, n), (e, n)

eucalg Die Implementierung der Funktion wird später besprochen.

Zu diesem Zeitpunkt ist die Schlüsselpaargenerierungsfunktion wie folgt:

def create_keys():
 p = genprime(1024)
 q = genprime(1024)
 n = p * q
 lambda_n = (p - 1) * (q - 1)
 e = 35537
 d = eucalg(e, lambda_n)[0]
 if d < 0: d += lambda_n
 return (d, n), (e, n)

2. Implementierung der Verschlüsselung und Entschlüsselung

Der Prozess der Verschlüsselung und Entschlüsselung ist der gleiche: Verschlüsselung mit öffentlichem Schlüssel, Entschlüsselung mit privatem Schlüssel und umgekehrt, privat Schlüsselverschlüsselung, öffentliche Schlüsselentschlüsselung, aber ersteres wird als Verschlüsselung und letzteres als Signatur bezeichnet.

Die spezifische Funktionsimplementierung lautet wie folgt:

def encrypt_data(data,key):
e_data = []
for d in data:
 e = modpow(d, key[0], key[1])
 e_data.append(e)
return e_data

## 加密和解密的逻辑完全一样
decrypt_data = encrypt_data

Hier wird die Funktion modpow verwendet, mit der die Formel b^e % n = r berechnet wird.

• Wenn es sich um einen Verschlüsselungsprozess handelt, dann ist b der Klartext, (n,e) der öffentliche Schlüssel und r der Chiffretext.
• Wenn es sich um einen Entschlüsselungsprozess handelt, dann ist b der Chiffretext, (n, d) der private Schlüssel und r der berühmte Text.

modpow ist wie folgt definiert:

def modpow(b, e, n):
 # find length of e in bits
 tst = 1
 siz = 0
 while e >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the result
 r = 1
 for i in range(siz, -1, -1):
r = (r * r) % n
if (e >> i) & 1: r = (r * b) % n
 return r

3. Generierungsfunktion für zufällige Primzahlen

Generierungsfunktion für zufällige Primzahlen, die Matrixmultiplikation und Fibonacci-Folge verwendet, was die Bedeutung der Mathematik für Algorithmen zeigt.

# matrix multiplication
def sqmatrixmul(m1, m2, w, mod):
 mr = [[0 for j in range(w)] for i in range(w)]
 for i in range(w):
for j in range(w):
 for k in range(w):
mr[i][j] = (mr[i][j] + m1[i][k] * m2[k][j]) % mod
 return mr

# fibonacci calculator
def fib(x, mod):
 if x < 3: return 1
 x -= 2
 # find length of e in bits
 tst = 1
 siz = 0
 while x >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the matrix
 fm = [
# function matrix
[0, 1],
[1, 1]
 ]
 rm = [
# result matrix
# (identity)
[1, 0],
[0, 1]
 ]
 for i in range(siz, -1, -1):
rm = sqmatrixmul(rm, rm, 2, mod)
if (x >> i) & 1:
 rm = sqmatrixmul(rm, fm, 2, mod)

 # second row of resulting vector is result
 return (rm[1][0] + rm[1][1]) % mod

def genprime(siz):
 while True:
num = (1 << (siz - 1)) + secrets.randbits(siz - 1) - 10;
# num must be 3 or 7 (mod 10)
num -= num % 10
num += 3 # 3 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num
num += 5 # 7 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num

4. Implementierung der Eucalg-Funktion

Die Essenz der Funktion besteht darin, die Lösung der folgenden linearen Gleichung von zwei Variablen zu finden:

e * x - lambda_n * y =1

Spezifischer Code:

def eucalg(a, b):
 # make a the bigger one and b the lesser one
 swapped = False
 if a < b:
a, b = b, a
swapped = True
 # ca and cb store current a and b in form of
 # coefficients with initial a and b
 # a' = ca[0] * a + ca[1] * b
 # b' = cb[0] * a + cb[1] * b
 ca = (1, 0)
 cb = (0, 1)
 while b != 0:
# k denotes how many times number b
# can be substracted from a
k = a // b
# swap a and b so b is always the lesser one
a, b, ca, cb = b, a-b*k, cb, (ca[0]-k*cb[0], ca[1]-k*cb[1])
 if swapped:
return (ca[1], ca[0])
 else:
return ca

5. Test

test.py-Skriptverwendungsmethode :

1), Generieren Sie den Schlüssel

python test.py make-keys rsakey

Der öffentliche Schlüssel wird in rsakey.pub gespeichert, und der private Schlüssel wird in rsakey.priv gespeichert

2), verschlüsseln Sie den Dateiinhalt

Wenn eine Datei im Klartext vorliegt .txt:

python test.py encrypt 明文.txt from rsakey to 密文.txt

generiert Chiffretext .txt

3. Entschlüsselt den Dateiinhalt

Wenn eine Datei ciphertext.txt vorhanden ist:

python test.py decrypt 密文.txt as rsakey to 解密后.txt

generiert eine entschlüsselte .txt-Datei

Abschlussworte

Dieser Artikel enthält eine einfache Implementierung des RSA-Algorithmus in Python, die zum Verständnis des RSA-Algorithmus beitragen kann.

Das obige ist der detaillierte Inhalt vonVerwenden Sie Python, um die RSA-Verschlüsselung und -Entschlüsselung zu implementieren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!