
In diesem Artikel „Schnelle kontrafaktische Inferenz für geschichtsbasiertes Verstärkungslernen“ wird ein schneller Kausalinferenzalgorithmus vorgeschlagen, der die rechnerische Komplexität der Kausalinferenz erheblich reduziert – bis zu dem Punkt, an dem er mit dem Online-Grad des Verstärkungslernens kombiniert werden kann .
Der theoretische Beitrag dieses Artikels besteht hauptsächlich aus zwei Punkten:
1. Es wird ein gemittelter kausaler Effekt vorgeschlagen. 2. Erweitern Sie das berühmte Backdoor-Kriterium von der univariaten Interventionseffektschätzung auf die multivariable Interventionseffektschätzung, die als Step-Backdoor-Kriterium bezeichnet wird.
Hintergrund
Sie müssen Grundkenntnisse über teilweise beobachtbares Verstärkungslernen und kausale Schlussfolgerungen vorbereiten. Ich werde hier nicht zu viel vorstellen, aber hier sind ein paar Portale:Teilweise beobachtbares Verstärkungslernen:
# 🎜 🎜#POMDP-Erklärung https://www.zhihu.com/zvideo/1326278888684187648
Kausale Argumentation: # 🎜 🎜#Kausales Denken in tiefen neuronalen Netzenhttps://zhuanlan.zhihu.com/p/425331915
MotivationAus historischen Informationen extrahieren /Encoding-Funktionen sind das grundlegende Mittel, um teilweise beobachtbares Verstärkungslernen zu lösen. Die gängige Methode besteht darin, das Sequence-to-Sequence-Modell (seq2seq) zum Codieren des Verlaufs zu verwenden. In diese Kategorie fallen beispielsweise die in diesem Bereich beliebten LSTM/GRU/NTM/Transformer-Verstärkungslernmethoden. Gemeinsam ist dieser Art von Methode, dass die Geschichte
basierend auf derKorrelation zwischen historischen Informationen und Lernsignalen (Umweltbelohnungen) kodiert wird, d. h. je größer die Korrelation einer historischen Information ist , je größer das zugewiesene Gewicht.
, die durch die Stichprobenentnahme verursacht wird, nicht beseitigen. Geben Sie ein Beispiel für das Aufnehmen eines Schlüssels zum Öffnen der Tür, wie im Bild unten gezeigt:
Hier Es hängt nur davon ab, ob der Agent die Tür öffnen kann. Ob der Schlüssel in der Geschichte erhalten wurde, hängt nicht von anderen Zuständen in der Geschichte ab. Wenn die Sampling-Strategie des Agenten jedoch Präferenzen für einige Pfade vorsieht, führt dies zu einer hohen Korrelation zwischen den Zuständen auf diesen bevorzugten Pfaden. Nachdem der Agent beispielsweise den Schlüssel erhalten hat, neigt er dazu, die Tür über den oberen Pfad zu öffnen, anstatt über den unteren Pfad, um die Tür zu öffnen, wodurch die Angelegenheit des Türöffnens stark mit dem Fernseher korreliert. Dieser Art von nicht-kausalem, aber hochrelevantem Zustand wird von seq2seq ein relativ hohes Gewicht verliehen, wodurch die codierten historischen Informationen sehr redundant werden. Wenn wir in diesem Beispiel die Korrelation zwischen dem Fernseher und der Türöffnung schätzen, gibt es aufgrund des Vorhandenseins des Schlüssels eine verwirrend hohe Korrelation zwischen beiden. Um die tatsächliche Auswirkung des Öffnens einer TV-Tür abzuschätzen, muss dieser verwirrende Zusammenhang beseitigt werden.
Diese verwirrende Korrelation kann durch Do-Kalkül im Kausalschluss [1] entfernt werden:Trennung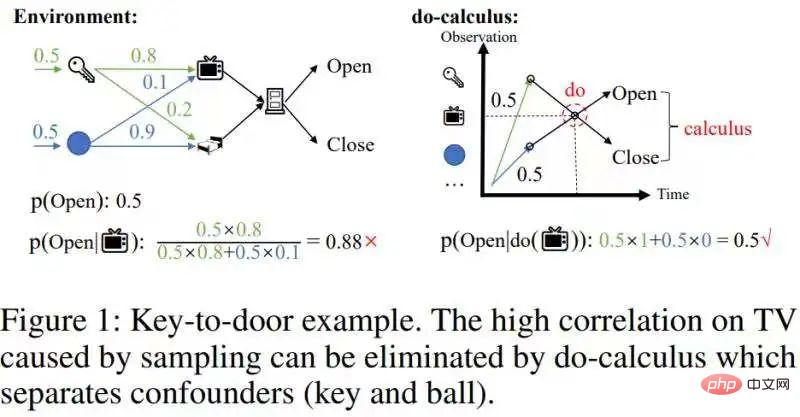 Potenziell verwirrend# 🎜🎜#Hintertürvariable
Potenziell verwirrend# 🎜🎜#Hintertürvariable
bedingte Wahrscheinlichkeit von p(Offen|, Schlüssel/Ball) umgewandelt wird. Integrieren Sie #🎜 🎜# auf der Hintertürvariablen (Schlüssel/Kugel) (rechtes Bild von Abbildung 1) und erhalten Sie den tatsächlichen Effekt p(Open|do( ))=0,5. Da es relativ selten historische Zustände mit kausalen Auswirkungen gibt, kann der Umfang historischer Zustände durch Entfernen verwirrender Korrelationen erheblich reduziert werden.
Deshalb hoffen wir, kausale Schlussfolgerungen zu verwenden, um verwirrende Korrelationen in historischen Stichproben zu entfernen, und verwenden dann seq2seq, um den Verlauf zu kodieren, um eine kompaktere historische Darstellung zu erhalten. (Motivation für diesen Artikel) Der wissenschaftliche Link https ist beigefügt: ://blog.csdn.net/qq_31063727/article/details/118672598 Die Durchführung kausaler Schlussfolgerungen in historischen Sequenzen unterscheidet sich von allgemeinen kausalen Schlussfolgerungsproblemen. Die -Variable in der historischen Sequenz hat sowohl Zeit- als auch Raumdimensionen , also eine Beobachtungs-Zeit-Kombination Frühere kausale Inferenzmethoden basierten auf univariater Interventionserkennung und konnten jeweils nur eine Variable verarbeiten. Das Durchführen von Kausalschlussfolgerungen in einem großen historischen Zustand führt zu extrem hoher Zeitkomplexität, was die Kombination mit Online-RL-Algorithmen erschwert. [2] Hinweis: Die formale Definition der kausalen Wirkung einer univariaten Intervention lautet wie folgt Wie in der Abbildung oben gezeigt, ist es angesichts der Geschichte notwendig, #🎜 zu schätzen 🎜##🎜🎜 #Für die kausale Wirkung der Übertragungsvariablen führen Sie die folgenden zwei Schritte aus: 1) In den historischen Zustand eingreifen # 🎜🎜##🎜🎜 #, 2) Den vorherigen historischen Zustand als Hintertürvariable nehmen, #🎜 🎜# Berechnen Sie als Antwortvariable das folgende Integral, das den erforderlichen kausalen Effekt darstellt 🎜#Da die univariate Interventionserkennung schwer mit Online-RL zu kombinieren ist, ist es notwendig, multivariate Interventionserkennungsmethoden zu entwickeln. IdeeDie Kernbeobachtung (Hypothese) dieses Artikels ist, dass Aber die kausale Wirkung ist in der Zeitdimension nicht gering Basierend auf den beiden oben genannten Beobachtungen besteht unsere Kernidee darin, bedeutet die Mittelung der Kausaleffekte mehrerer historischer Zustände über die Zeit (spezifische Definitionen finden Sie im Originaltext). Basierend auf dieser Idee konzentrieren wir uns auf das Problem: Das zu lösende Kernproblem besteht darin, wiedie gemeinsame kausale Wirkung des Eingreifens in mehreren verschiedenen Zeitschritten Wir verbessern das Hintertürkriterium und schlagen ein Kriterium vor, das zur Schätzung multivariabler Schätzungen des Gelenkinterventionseffekts geeignet ist. Für zwei beliebige intervenierte Variablen Schritt-Hintertür-Anpassungskriterium (Schritt-Hintertür-Anpassungsformel) Dieses Kriterium trennt andere Variablen zwischen den Variablen zweier benachbarter Zeitschritte, die als Stepping-Backdoor-Variablen bezeichnet werden. In einem Kausaldiagramm, das dieses Kriterium erfüllt, können wir die gemeinsame kausale Wirkung zweier beliebiger dazwischenliegender Variablen abschätzen. Es umfasst zwei Schritte: Schritt 1. Verwenden Sie die Variable, die zum Zeitpunkt des Zeitschritts kleiner als i ist, als Hintertürvariable, um den kausalen Effekt von do Theorem 1. Wenn bei einem Satz intervenierter Variablen mit unterschiedlichen Zeitstempeln alle zwei zeitlich benachbarten Variablen die Step-Backdoor-Anpassungsformel erfüllen, dann ist der gesamte kausale Effekt kann geschätzt werden mit Speziell für das teilweise beobachtbare Verstärkungslernproblem gibt es nach Ersetzen von x in der obigen Formel durch Beobachtung o die folgende Formel zur Berechnung des Kausaleffekts: Theorem 2. Gegeben sind An dieser Stelle gibt das Papier eine Formel zur Berechnung räumlicher Kausaleffekte (d. h. zeitlich gemittelter Kausaleffekte) an. Diese Methode reduziert die Anzahl der Eingriffe von O().
Einschränkungen: Das kausale Denken in der räumlichen Dimension hat den historischen Maßstab bereits ausreichend komprimiert. Obwohl kausale Schlussfolgerungen in der Zeitdimension die historische Skala weiter komprimieren können, da die Rechenkomplexität ausgeglichen werden muss, behält dieser Artikel die Korrelationsinferenz in der Zeitdimension bei (unter Verwendung von LSTM End-to-End für historische Zustände mit räumlichen Kausaleffekten) und verwendet kein kausales Denken. Verifizierung
Richtungen für zukünftige Erweiterungen Zwei Punkte zum Einstieg in die Diskussion: 1. HCI ist nicht auf die Art des verstärkenden Lernens beschränkt. Obwohl dieser Artikel Online-RL untersucht, kann HCI natürlich auch auf Offline-RL, modellbasiertes RL usw. ausgeweitet werden, und Sie können sogar erwägen, HCI auf Nachahmungslernen anzuwenden 2 Aufmerksamkeitsmethode – Sequenzpunkte mit kausalem Effekt erhalten ein Aufmerksamkeitsgewicht von 1, andernfalls erhalten sie ein Aufmerksamkeitsgewicht von 0. Aus dieser Perspektive können einige Sequenzvorhersageprobleme möglicherweise auch mithilfe von HCI gelöst werden. Schwierigkeit
 , wobei o die Beobachtung und t die ist Zeitstempel (Phase Im Vergleich dazu ist MDP sehr freundlich, der Markov-Zustand hat nur räumliche Dimensionen). Durch die Überlappung der beiden Dimensionen ist der Umfang historischer Beobachtungen recht groß. Verwenden Sie
, wobei o die Beobachtung und t die ist Zeitstempel (Phase Im Vergleich dazu ist MDP sehr freundlich, der Markov-Zustand hat nur räumliche Dimensionen). Durch die Überlappung der beiden Dimensionen ist der Umfang historischer Beobachtungen recht groß. Verwenden Sie  , um die Anzahl der Beobachtungswerte auf jedem Zeitstempel darzustellen, und verwenden Sie T, um die Gesamtlänge darzustellen Dann gibt es
, um die Anzahl der Beobachtungswerte auf jedem Zeitstempel darzustellen, und verwenden Sie T, um die Gesamtlänge darzustellen Dann gibt es  Arten von Werten für den historischen Zustand (der reguläre Körper O( ) ist das Komplexitätssymbol). [2]
Arten von Werten für den historischen Zustand (der reguläre Körper O( ) ist das Komplexitätssymbol). [2]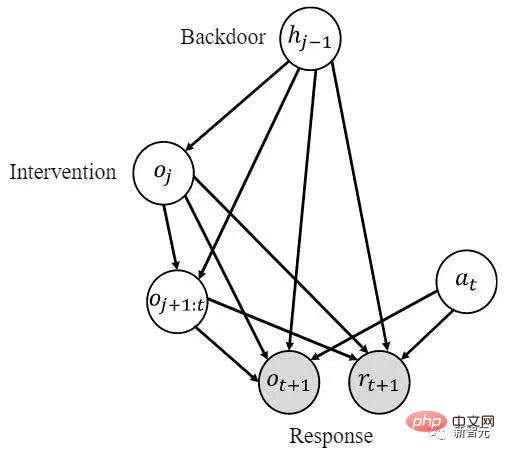
 Es ist auch ein Schlüssel zum Öffnen der Tür. Der Schlüssel kann vom Agenten meistens beobachtet werden. Die Dichte der kausalen Wirkungen in der Zeitdimension verhindert die Durchführung multivariater Interventionen – es ist unmöglich, eine große Anzahl historischer Zustände ohne kausale Wirkungen auf einmal zu entfernen.
Es ist auch ein Schlüssel zum Öffnen der Tür. Der Schlüssel kann vom Agenten meistens beobachtet werden. Die Dichte der kausalen Wirkungen in der Zeitdimension verhindert die Durchführung multivariater Interventionen – es ist unmöglich, eine große Anzahl historischer Zustände ohne kausale Wirkungen auf einmal zu entfernen. Nutzen Sie die Sparsamkeit in der räumlichen Dimension, um die Anzahl der Eingriffe deutlich zu reduzieren.
Um allein den räumlichen Kausaleffekt abzuschätzen, schlagen wir vor, zunächst den zeitlichen Durchschnitt des Kausaleffekts zu ermitteln.  mit derselben Variablen (bezeichnet als ) zu berechnen ). Dies liegt daran, dass das Hintertürkriterium nicht für die gemeinsame Intervention mehrerer historischer Variablen gilt: Wie in der folgenden Abbildung gezeigt, können Sie unter Berücksichtigung der gemeinsamen Intervention der dualen Variablen
mit derselben Variablen (bezeichnet als ) zu berechnen ). Dies liegt daran, dass das Hintertürkriterium nicht für die gemeinsame Intervention mehrerer historischer Variablen gilt: Wie in der folgenden Abbildung gezeigt, können Sie unter Berücksichtigung der gemeinsamen Intervention der dualen Variablen 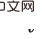 und
und  diesen Teil von sehen
diesen Teil von sehen  im späteren Zeitschritt Die Hintertürvariable enthält
im späteren Zeitschritt Die Hintertürvariable enthält  , und es gibt keine gemeinsame Hintertürvariable zwischen den beiden.
, und es gibt keine gemeinsame Hintertürvariable zwischen den beiden. 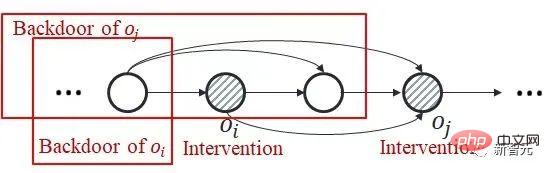
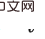 und
und 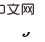 (i
(i
 abzuschätzen. Schritt 2. Verwenden Sie die ermittelte Hintertürvariable und die ermittelte
abzuschätzen. Schritt 2. Verwenden Sie die ermittelte Hintertürvariable und die ermittelte  als Bedingungen, wobei die Variablen zwischen
als Bedingungen, wobei die Variablen zwischen  und
und  als neue Hintertürvariablen über
als neue Hintertürvariablen über 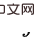 (d. h. schrittweise Hintertürvariablen über
(d. h. schrittweise Hintertürvariablen über 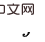 und
und  ) verwendet werden, um die
) verwendet werden, um die  bedingte Kausalität von do abzuschätzen
bedingte Kausalität von do abzuschätzen  Wirkung . Dann ist der gemeinsame kausale Effekt das Produktintegral dieser beiden Teile. Das Schritt-Hintertür-Kriterium verwendet zwei Schritte des gewöhnlichen Hintertür-Kriteriums, wie in der folgenden Abbildung dargestellt. Die obige Formel verwendet einen allgemeineren variablen Indikator X.
Wirkung . Dann ist der gemeinsame kausale Effekt das Produktintegral dieser beiden Teile. Das Schritt-Hintertür-Kriterium verwendet zwei Schritte des gewöhnlichen Hintertür-Kriteriums, wie in der folgenden Abbildung dargestellt. Die obige Formel verwendet einen allgemeineren variablen Indikator X. 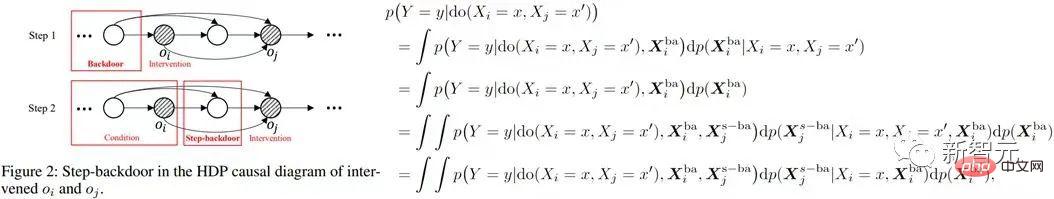
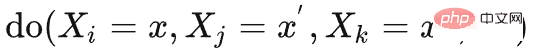
 und
und  , der Kausaleffekt of Do (o) kann geschätzt werden durch
, der Kausaleffekt of Do (o) kann geschätzt werden durch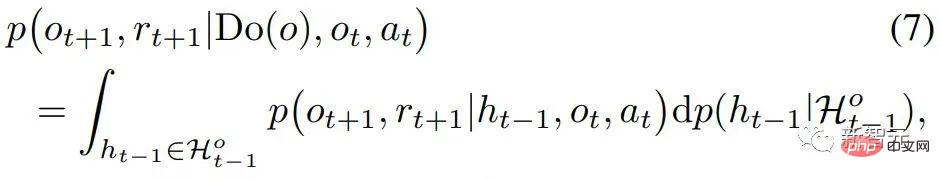
 ) bis O (
) bis O ( ). Der nächste Schritt besteht darin, die spärlichen räumlichen Kausaleffekte (die zu Beginn dieses Kapitels erwähnt wurden) zu nutzen, um die Anzahl der Interventionen weiter exponentiell zu reduzieren. Ersetzen Sie den Eingriff in eine Beobachtung durch den Eingriff in einen Beobachtungsunterraum – dies ist eine gängige Idee, um Sparsity zu nutzen und Berechnungen zu beschleunigen (siehe Originalartikel). In diesem Artikel wird ein schneller kontrafaktischer Inferenzalgorithmus namens Tree-based History Counterfactual Inference (T-HCI) entwickelt, der hier nicht im Detail beschrieben wird (Einzelheiten finden Sie im Originaltext). Tatsächlich können viele historische Kausalinferenzalgorithmen auf der Grundlage des Stepping-Backdoor-Kriteriums entwickelt werden, und T-HCI ist nur einer davon. Das Endergebnis ist Vorschlag 3 (Grob-zu-Fein-CI). Wenn
). Der nächste Schritt besteht darin, die spärlichen räumlichen Kausaleffekte (die zu Beginn dieses Kapitels erwähnt wurden) zu nutzen, um die Anzahl der Interventionen weiter exponentiell zu reduzieren. Ersetzen Sie den Eingriff in eine Beobachtung durch den Eingriff in einen Beobachtungsunterraum – dies ist eine gängige Idee, um Sparsity zu nutzen und Berechnungen zu beschleunigen (siehe Originalartikel). In diesem Artikel wird ein schneller kontrafaktischer Inferenzalgorithmus namens Tree-based History Counterfactual Inference (T-HCI) entwickelt, der hier nicht im Detail beschrieben wird (Einzelheiten finden Sie im Originaltext). Tatsächlich können viele historische Kausalinferenzalgorithmen auf der Grundlage des Stepping-Backdoor-Kriteriums entwickelt werden, und T-HCI ist nur einer davon. Das Endergebnis ist Vorschlag 3 (Grob-zu-Fein-CI). Wenn , beträgt die Anzahl der Eingriffe für Grob-zu-Fein-CI.
, beträgt die Anzahl der Eingriffe für Grob-zu-Fein-CI. 
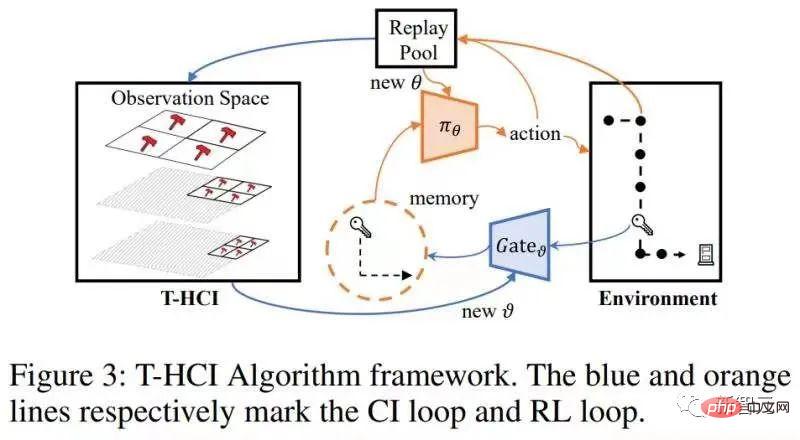 Der Algorithmus enthält zwei Schleifen, eine ist die T-HCI-Schleife und die andere ist die Richtlinienlernschleife. Die beiden werden ausgetauscht: in der Richtlinie In der Lernschleife lernt der Agent eine bestimmte Anzahl von Runden und speichert die Proben im Wiederholungspool. In der T-HCI-Schleife werden die gespeicherten Proben verwendet, um den oben genannten Kausalinferenzprozess durchzuführen.
Der Algorithmus enthält zwei Schleifen, eine ist die T-HCI-Schleife und die andere ist die Richtlinienlernschleife. Die beiden werden ausgetauscht: in der Richtlinie In der Lernschleife lernt der Agent eine bestimmte Anzahl von Runden und speichert die Proben im Wiederholungspool. In der T-HCI-Schleife werden die gespeicherten Proben verwendet, um den oben genannten Kausalinferenzprozess durchzuführen. Drei Punkte wurden experimentell überprüft und auf die vorherigen Behauptungen reagiert: 1) Kann T-HCI die Probeneffizienz von RL-Methoden verbessern? 2) Ist der Rechenaufwand von T-HCI in der Praxis akzeptabel? -HCI-Minenbeobachtungen mit kausalen Auswirkungen? Einzelheiten finden Sie im experimentellen Kapitel des Artikels, daher werde ich hier keinen Platz einnehmen. Interessierte Freunde können mir natürlich auch eine private Nachricht/Kommentar schicken.
Das obige ist der detaillierte Inhalt vonZum ersten Mal vorgestellt! Verwendung kausaler Schlussfolgerungen, um teilweise beobachtbares Verstärkungslernen durchzuführen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




