Die Zahl der Arbeiten ist in den letzten zehn Jahren stark gestiegen. Wie öffnet Deep Learning langsam die Tür zum mathematischen Denken?

Mathematisches Denken ist eine wichtige Manifestation der menschlichen Intelligenz und ermöglicht es uns, numerische Daten und Sprache zu verstehen und Entscheidungen auf der Grundlage dieser zu treffen. Mathematische Argumentation findet in einer Vielzahl von Bereichen Anwendung, darunter Naturwissenschaften, Technik, Finanzen und Alltagsleben, und umfasst eine Reihe von Fähigkeiten, von Grundfertigkeiten wie Mustererkennung und Zahlenrechnen bis hin zu fortgeschrittenen Fertigkeiten wie Problemlösung, logisches Denken und abstraktes Denken.

Die Entwicklung von KI-Systemen, die mathematische Probleme lösen und mathematische Theoreme beweisen können, ist seit langem ein Forschungsschwerpunkt in den Bereichen maschinelles Lernen und Verarbeitung natürlicher Sprache. Auch dieser stammt aus den 1960er Jahren.

In den letzten zehn Jahren seit dem Aufkommen von Deep Learning ist das Interesse der Menschen an diesem Bereich erheblich gewachsen:

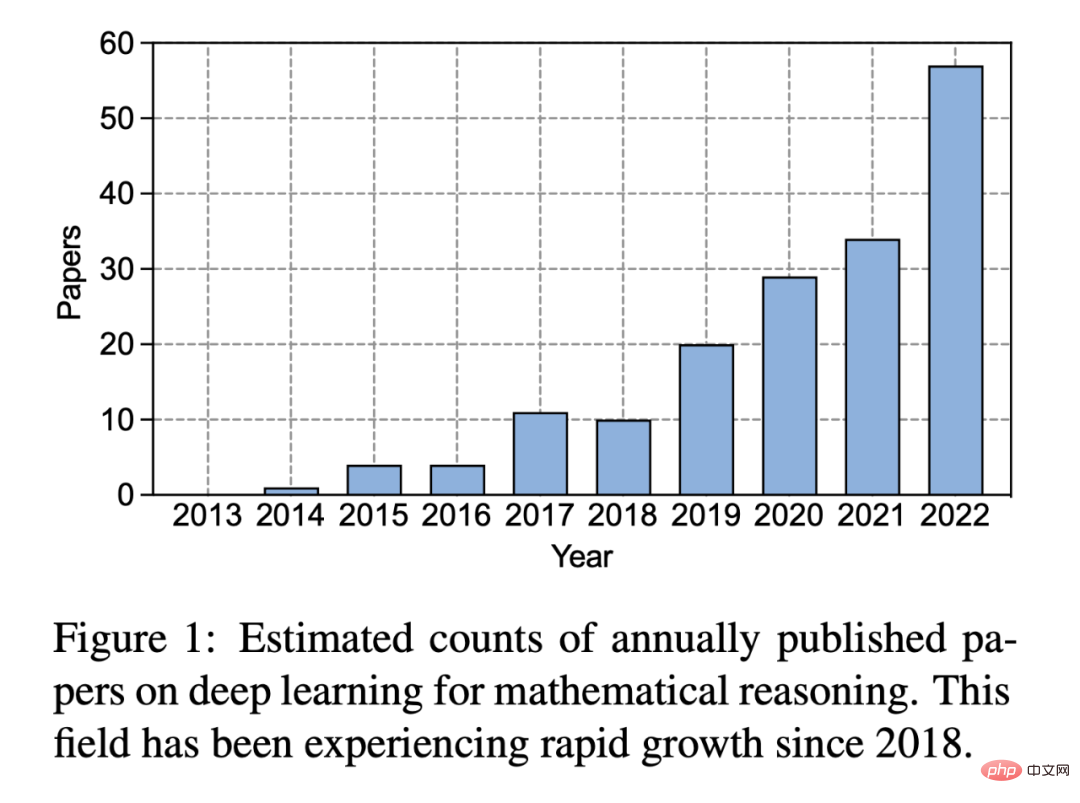
Abbildung 1: Geschätzte Anzahl der jährlich veröffentlichten Deep-Learning-Aufsätze zum Thema mathematisches Denken . Seit 2018 verzeichnet dieser Bereich ein rasantes Wachstum.

Deep Learning hat bei verschiedenen Aufgaben der Verarbeitung natürlicher Sprache, wie etwa der Beantwortung von Fragen und der maschinellen Übersetzung, großen Erfolg gezeigt. Ebenso haben Forscher verschiedene neuronale Netzwerkmethoden für das mathematische Denken entwickelt, die sich bei der Bewältigung komplexer Aufgaben wie Textaufgaben, Theorembeweisen und geometrischer Problemlösung als wirksam erwiesen haben. Beispielsweise übernehmen Deep-Learning-basierte Anwendungsproblemlöser ein Sequenz-zu-Sequenz-Framework und verwenden einen Aufmerksamkeitsmechanismus als Zwischenschritt, um mathematische Ausdrücke zu generieren. Darüber hinaus haben vorab trainierte Sprachmodelle mit groß angelegten Korpora- und Transformer-Modellen vielversprechende Ergebnisse bei verschiedenen mathematischen Aufgaben erzielt. In jüngster Zeit haben große Sprachmodelle wie GPT-3 das Gebiet des mathematischen Denkens weiter vorangetrieben, indem sie beeindruckende Fähigkeiten im komplexen Denken und im kontextuellen Lernen demonstriert haben.

In einem kürzlich veröffentlichten Bericht untersuchten Forscher der UCLA und anderer Institutionen systematisch die Fortschritte des Deep Learning im mathematischen Denken.

Papierlink: https://arxiv.org/pdf/2212.10535.pdf

Projektadresse: https://github.com/lupantech/dl4math

Spec ific In diesem Artikel werden insbesondere verschiedene Aufgaben und Datensätze erörtert (Abschnitt 2) und Fortschritte bei neuronalen Netzen (Abschnitt 3) und vorab trainierten Sprachmodellen (Abschnitt 4) im Bereich der Mathematik untersucht. Die schnelle Entwicklung des kontextuellen Lernens großer Sprachmodelle im mathematischen Denken wird ebenfalls untersucht (Abschnitt 5). Der Artikel analysiert bestehende Benchmarks weiter und stellt fest, dass multimodalen und ressourcenarmen Umgebungen weniger Aufmerksamkeit geschenkt wird (Abschnitt 6.1). Evidenzbasierte Forschung zeigt, dass die aktuellen Darstellungen der Rechenkapazitäten unzureichend sind und Deep-Learning-Methoden in Bezug auf mathematisches Denken inkonsistent sind (Abschnitt 6.2). Anschließend schlagen die Autoren Verbesserungen der aktuellen Arbeit in Bezug auf Verallgemeinerung und Robustheit, vertrauenswürdiges Denken, Lernen aus Feedback und multimodales mathematisches Denken vor (Abschnitt 7).

Aufgaben und Datensätze

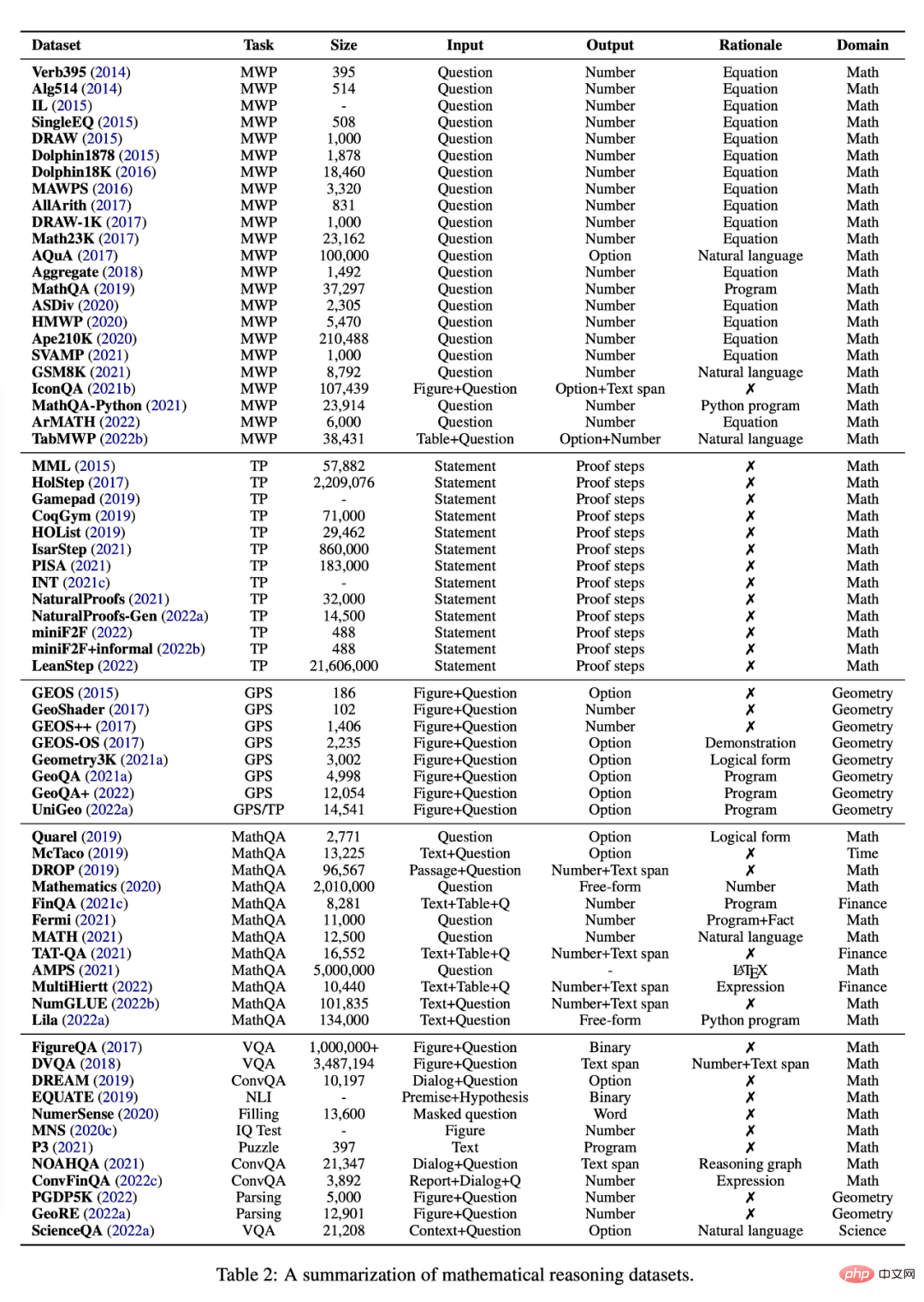
In diesem Abschnitt werden die verschiedenen Aufgaben und Datensätze untersucht, die derzeit für das Studium des mathematischen Denkens mithilfe von Deep-Learning-Methoden verfügbar sind, siehe Tabelle 2.

Wortaufgabe (mathematische Wortaufgabe)

Eine Wortaufgabe enthält eine kurze Beschreibung, an der Personen, Entitäten und Mengen beteiligt sind. Die mathematische Beziehung kann durch eine Reihe von Gleichungen modelliert werden Gleichung zeigt die endgültige Antwort auf die Frage. Tabelle 1 ist ein typisches Beispiel. Eine Frage umfasst die vier grundlegenden mathematischen Operationen Addition, Subtraktion, Multiplikation und Division mit einzelnen oder mehreren Schritten. Die Herausforderung bei Anwendungsproblemen für NLP-Systeme liegt in der Nachfrage nach Sprachverständnis, semantischer Analyse und verschiedenen mathematischen Denkfähigkeiten.

Vorhandene Wortproblemdatensätze umfassen Fragen auf Grundschulniveau, die von Online-Lernwebsites zusammengestellt, aus Lehrbüchern gesammelt oder von Menschen manuell mit Anmerkungen versehen wurden. Frühe Datensätze zu Textaufgaben waren relativ klein oder auf eine kleine Anzahl von Schritten beschränkt. Einige neuere Datensätze zielen darauf ab, die Vielfalt und Schwierigkeit des Problems zu erhöhen. Beispielsweise besteht Ape210K, der derzeit größte öffentliche Aufgabensatz, aus 210.000 Wortaufgaben für Grundschulen, während Aufgaben in GSM8K bis zu 8-stufige Lösungen umfassen können. SVAMP ist ein Benchmark, der die Robustheit von Deep-Learning-Modellen bei Textproblemen mit einfachen Variationen testet. Einige kürzlich erstellte Datensätze umfassen auch andere Modalitäten als Text. IconQA bietet beispielsweise ein abstraktes Diagramm als visuellen Hintergrund, während TabMWP für jede Frage einen tabellarischen Hintergrund bereitstellt.

Die meisten Textaufgaben-Datensätze liefern Gründe für die Annotation von Gleichungen als Lösungen (siehe Tabelle 1). Um die Leistung und Interpretierbarkeit erlernter Löser zu verbessern, wird MathQA mit präzisen Rechenprozeduren annotiert und MathQA-Python stellt konkrete Python-Prozeduren bereit. Andere Datensätze kommentieren Fragen mit mehrstufigen Lösungen in natürlicher Sprache, die als besser für das menschliche Lesen geeignet gelten. Lila kommentierte viele der zuvor erwähnten Textaufgaben-Datensätze mithilfe der Prinzipien der Python-Programmierung.

Theoretischer Beweis

Die Automatisierung des Theorembeweises ist eine langfristige Herausforderung im Bereich der KI. Das Problem besteht normalerweise darin, die Wahrheit eines mathematischen Theorems durch eine Reihe logischer Argumente zu beweisen. Das Beweisen von Theoremen erfordert eine Vielzahl von Fertigkeiten, wie z. B. die Auswahl effizienter Mehrschrittstrategien, die Nutzung von Hintergrundwissen und die Durchführung symbolischer Operationen wie Arithmetik oder Ableitungen.

In letzter Zeit besteht ein zunehmendes Interesse an der Verwendung von Sprachmodellen zur Theorembeweisung in formalen interaktiven Theoremprüfern (ITPs). Ein Theorem wird in der Programmiersprache von ITP formuliert und dann durch die Generierung von „Beweisschritten“ vereinfacht, bis es auf eine bekannte Tatsache reduziert wird. Das Ergebnis ist eine Abfolge von Schritten, die einen verifizierten Beweis darstellen.

Informelles Beweisen von Theoremen schlägt ein alternatives Medium zum Beweisen von Theoremen vor, bei dem Aussagen und Beweise in einer Hybridform aus natürlicher Sprache und „standardmäßiger“ mathematischer Notation (wie LATEX) geschrieben und von Menschen auf ihre Richtigkeit überprüft werden.

Ein aufstrebendes Forschungsgebiet zielt darauf ab, Elemente der informellen und formalen Beweisführung von Theoremen zu kombinieren. Beispielsweise untersuchen Wu et al. (2022b) die Übersetzung informeller Aussagen in formelle Aussagen, während Jiang et al. (2022b) eine neue Version des miniF2F-Benchmarks veröffentlicht hat, die informelle Aussagen und Beweise hinzufügt, genannt miniF2F+informal. Jiang et al. (2022b) untersuchen die Umwandlung bereitgestellter (oder generierter) informeller Beweise in formale Beweise.

Geometrische Probleme

Automatisiertes Lösen geometrischer Probleme (GPS) ist auch eine langjährige Aufgabe der künstlichen Intelligenz in der mathematischen Denkforschung und hat in den letzten Jahren große Aufmerksamkeit erregt. Im Gegensatz zu Textaufgaben bestehen Geometrieprobleme aus Textbeschreibungen in natürlicher Sprache und geometrischen Figuren. Wie in Abbildung 2 dargestellt, beschreibt die multimodale Eingabe Entitäten, Eigenschaften und Beziehungen geometrischer Elemente, während das Ziel darin besteht, numerische Lösungen für unbekannte Variablen zu finden. GPS ist aufgrund der erforderlichen komplexen Fähigkeiten eine anspruchsvolle Aufgabe für Deep-Learning-Methoden. Dazu gehört die Fähigkeit, multimodale Informationen zu analysieren, sich auf symbolische Abstraktion einzulassen, Theoremwissen zu nutzen und sich auf quantitatives Denken einzulassen.

Frühe Datensätze haben die Forschung auf diesem Gebiet gefördert, allerdings sind diese Datensätze relativ klein oder nicht öffentlich verfügbar, was die Entwicklung von Deep-Learning-Methoden einschränkt. Um diese Einschränkung zu beheben, haben Lu et al. den Geometry3K-Datensatz erstellt, der aus 3002 Multiple-Choice-Geometriefragen besteht, die in einer einheitlichen logischen Form für multimodale Eingaben kommentiert sind. Kürzlich wurden größere Datensätze wie GeoQA, GeoQA+ und UniGeo eingeführt und mit Programmen versehen, die von neuronalen Lösern erlernt und ausgeführt werden können, um endgültige Antworten zu erhalten.

Mathe-Fragen und Antworten

Neueste Untersuchungen zeigen, dass das mathematische Argumentationssystem von SOTA möglicherweise „brüchig“ ist, d. Ergebnisse Leistung. Um dieses Problem zu lösen, wurden unter verschiedenen Gesichtspunkten neue Benchmarks vorgeschlagen. Der Mathematik-Datensatz (Saxton et al., 2020) umfasst viele verschiedene Arten mathematischer Probleme, die Arithmetik, Algebra, Wahrscheinlichkeitsrechnung und Analysis umfassen. Dieser Datensatz kann die algebraische Generalisierungsfähigkeit des Modells messen. In ähnlicher Weise besteht MATH (Hendrycks et al., 2021) aus anspruchsvoller Wettbewerbsmathematik, um die Problemlösungsfähigkeit eines Modells in komplexen Situationen zu messen.

Bei einigen Arbeiten wurde der Frageneingabe ein Tabellenhintergrund hinzugefügt. Beispielsweise sammeln FinQA, TAT-QA und MultiHiertt Fragen, deren Beantwortung Tabellenverständnis und numerisches Denken erfordert. Einige Studien haben einheitliche Benchmarks für das numerische Denken im großen Maßstab vorgeschlagen. NumGLUE (Mishra et al., 2022b) ist ein Multi-Task-Benchmark, der darauf abzielt, die Modellleistung bei acht verschiedenen Aufgaben zu bewerten. Mishra et al. 2022a haben diese Richtung vorangetrieben, indem sie Lila vorgeschlagen haben, das aus 23 Aufgaben zum numerischen Denken besteht, die ein breites Spektrum an mathematischen Themen, Sprachkomplexität, Frageformaten und Hintergrundwissensanforderungen abdecken.

KI hat auch bei anderen Arten quantitativer Probleme Erfolge erzielt. Zahlen, Diagramme und Zeichnungen beispielsweise sind wesentliche Medien, um große Informationsmengen prägnant zu vermitteln. FigureQA, DVQA, MNS, PGDP5K und GeoRE wurden alle eingeführt, um die Fähigkeit von Modellen zu untersuchen, über quantitative Beziehungen zwischen graphbasierten Entitäten nachzudenken. NumerSense untersucht, ob und inwieweit bestehende vortrainierte Sprachmodelle in der Lage sind, numerisches Common-Sense-Wissen zu erfassen. EQUATE formalisiert verschiedene Aspekte des quantitativen Denkens in einem Rahmen für das logische Denken in natürlicher Sprache. Quantitatives Denken kommt auch häufig in bestimmten Bereichen wie Finanzen, Wissenschaft und Programmierung vor. ConvFinQA führt beispielsweise numerisches Denken in Finanzberichten in Form von Konversationsfragen durch; ScienceQA umfasst numerisches Denken im wissenschaftlichen Bereich und P3 untersucht die funktionale Argumentationsfähigkeit von Deep-Learning-Modellen, um eine gültige Eingabe für die Rückgabe eines bestimmten Programms zu finden WAHR.

Neuronale Netze für mathematisches Denken

Für mehrere gängige neuronale Netze, die für mathematisches Denken verwendet werden, hat der Autor dieses Artikels auch eine Zusammenfassung durchgeführt. Neuronale Netze wurden erfolgreich auf mathematische Denkaufgaben wie Textaufgaben, Theorembeweise, Geometrieprobleme und Antworten auf mathematische Fragen angewendet. Seq2Seq-Modelle verwenden eine Encoder-Decoder-Architektur, die mathematisches Denken typischerweise als Aufgabe zur Sequenzgenerierung formalisiert. Die Grundidee dieser Methode besteht darin, Eingabesequenzen (z. B. mathematische Probleme) auf Ausgabesequenzen (z. B. Gleichungen, Programme und Beweise) abzubilden. Zu den gängigen Encodern und Decodern gehören Long Short-Term Memory Network (LSTM) und Gated Recurrent Unit (GRU). Umfangreiche Arbeiten haben gezeigt, dass Seq2Seq-Modelle Leistungsvorteile gegenüber früheren statistischen Lernmethoden haben, einschließlich ihrer bidirektionalen Varianten BiLSTM und BiGRU. DNS ist die erste Arbeit, die das Seq2Seq-Modell verwendet, um Sätze aus Textaufgaben in mathematische Gleichungen umzuwandeln.

Graphenbasiertes Netzwerk

Die Seq2Seq-Methode hat die Fähigkeit dazu Generieren Sie mathematische Ausdrücke im Stil und verlassen Sie sich nicht auf handgefertigte Funktionen. Mathematische Ausdrücke können in baumbasierte Strukturen wie abstrakte Syntaxbäume (AST) und graphbasierte Strukturen umgewandelt werden, die die strukturierten Informationen im Ausdruck beschreiben. Diese wichtigen Informationen werden jedoch durch den Seq2Seq-Ansatz nicht explizit modelliert. Um dieses Problem zu lösen, entwickelten Forscher graphbasierte neuronale Netze, um die Struktur in Ausdrücken explizit zu modellieren.

Sequence-to-Tree-Modelle (Seq2Tree) modellieren explizit die Baumstruktur beim Codieren der Ausgabesequenz. Beispielsweise haben Liu et al. ein Seq2Tree-Modell entworfen, um die AST-Informationen von Gleichungen besser zu nutzen. Im Gegensatz dazu wendet Seq2DAG beim Generieren von Gleichungen ein Sequenzdiagramm-Framework (Seq2Graph) an, da der Diagrammdecoder in der Lage ist, komplexe Beziehungen zwischen mehreren Variablen zu extrahieren. Bei der Codierung eingegebener mathematischer Sequenzen können auch graphbasierte Informationen eingebettet werden. Beispielsweise wendet ASTactic TreeLSTM auf AST an, um die Eingabeziele und Prämissen von Theorembeweisen darzustellen.

Aufmerksamkeitsbasiertes Netzwerk ​

Der Aufmerksamkeitsmechanismus wurde erfolgreich auf Probleme bei der Verarbeitung natürlicher Sprache und Computer Vision angewendet, wobei der verborgene Eingabevektor während des Dekodierungsprozesses berücksichtigt wurde. Forscher haben seine Rolle bei mathematischen Denkaufgaben untersucht, da es zur Identifizierung der wichtigsten Beziehungen zwischen mathematischen Konzepten verwendet werden kann. Beispielsweise ist MATH-EN ein Wortproblemlöser, der von durch Selbstaufmerksamkeit erlernten Informationen über weitreichende Abhängigkeiten profitiert. Aufmerksamkeitsbasierte Methoden wurden auch auf andere mathematische Denkaufgaben angewendet, beispielsweise auf Geometrieprobleme und das Beweisen von Theoremen. Um bessere Darstellungen zu extrahieren, wurden verschiedene Aufmerksamkeitsmechanismen untersucht, beispielsweise Group-ATT, das unterschiedliche Multi-Head-Aufmerksamkeit verwendet, um verschiedene Arten von MWP-Merkmalen zu extrahieren, und Graph-Aufmerksamkeit, die zur Extraktion wissensbewusster Informationen eingesetzt wird.

Andere neuronale Netze

Deep-Learning-Methoden für mathematische Denkaufgaben können auch andere neuronale Netze nutzen, beispielsweise Faltungs-Neuronale Netze und multimodale Netze. Einige Arbeiten verwenden Faltungsarchitekturen neuronaler Netzwerke zur Codierung von Eingabetexten, wodurch das Modell die Möglichkeit erhält, langfristige Beziehungen zwischen Symbolen in der Eingabe zu erfassen. Beispielsweise schlugen Irving et al. die erste Anwendung tiefer neuronaler Netze beim Beweisen von Theoremen vor, die für die Prämissenauswahl in großen Theorien auf Faltungsnetzen beruhten.

Multimodale mathematische Denkaufgaben, wie z. B. das Lösen geometrischer Probleme und graphbasiertes mathematisches Denken, werden als VQA-Fragen (Visual Question Answering) formalisiert. In diesem Bereich werden visuelle Eingaben mit ResNet oder Faster-RCNN codiert, während Textdarstellungen über GRU oder LTSM erhalten werden. Anschließend werden gemeinsame Darstellungen mithilfe multimodaler Fusionsmodelle wie BAN, FiLM und DAFA erlernt.

Andere tiefe neuronale Netzwerkstrukturen können auch für mathematische Überlegungen verwendet werden. Zhang et al. nutzten den Erfolg graphischer neuronaler Netze (GNN) beim räumlichen Denken und wandten ihn auf geometrische Probleme an. WaveNet wird zum Beweisen von Theoremen eingesetzt, da es longitudinale Zeitreihendaten lösen kann. Darüber hinaus wurde festgestellt, dass Transformer GRU bei der Generierung mathematischer Gleichungen in DDT übertrifft. Und MathDQN ist das erste Werk, das sich mit Reinforcement Learning zur Lösung mathematischer Wortprobleme beschäftigt und dabei vor allem seine leistungsstarken Suchfunktionen nutzt.

Vorab trainierte Sprachmodelle für mathematisches Denken

Vorab trainierte Sprachmodelle haben bei einer Vielzahl von NLP-Aufgaben erhebliche Leistungsverbesserungen gezeigt und werden auch auf mathematikbezogene Probleme angewendet Modelle Das Modell eignet sich gut zur Lösung von Wortproblemen und hilft beim Beweisen von Theoremen und anderen mathematischen Aufgaben. Die Verwendung für mathematische Überlegungen bringt jedoch mehrere Herausforderungen mit sich.

Erstens ist das vorab trainierte Sprachmodell nicht speziell auf mathematische Daten trainiert. Dies kann dazu führen, dass ihre Kompetenz bei mathematischen Aufgaben geringer ist als bei Aufgaben in natürlicher Sprache. Außerdem stehen im Vergleich zu Textdaten weniger mathematische oder wissenschaftliche Daten für umfangreiche Vorschulungen zur Verfügung.

Zweitens nimmt die Größe vorab trainierter Modelle immer weiter zu, was es teuer macht, ein ganzes Modell von Grund auf für eine bestimmte nachgelagerte Aufgabe zu trainieren.

Darüber hinaus können nachgelagerte Aufgaben unterschiedliche Eingabeformate oder -modalitäten verarbeiten, beispielsweise strukturierte Tabellen oder Diagramme. Um diese Herausforderungen zu bewältigen, müssen Forscher vorab trainierte Modelle verfeinern oder neuronale Architekturen für nachgelagerte Aufgaben anpassen.

Obwohl vorab trainierte Sprachmodelle eine große Menge an Sprachinformationen codieren können, kann es für das Modell allein aufgrund des Ziels der Sprachmodellierung schwierig sein, numerische Darstellung oder Denkfähigkeiten auf hohem Niveau zu erlernen. Vor diesem Hintergrund haben neuere Forschungsarbeiten die Vermittlung mathematikbezogener Kompetenzen in Kurse untersucht, die mit den Grundlagen beginnen.

Selbstüberwachtes Lernen von Mathematik

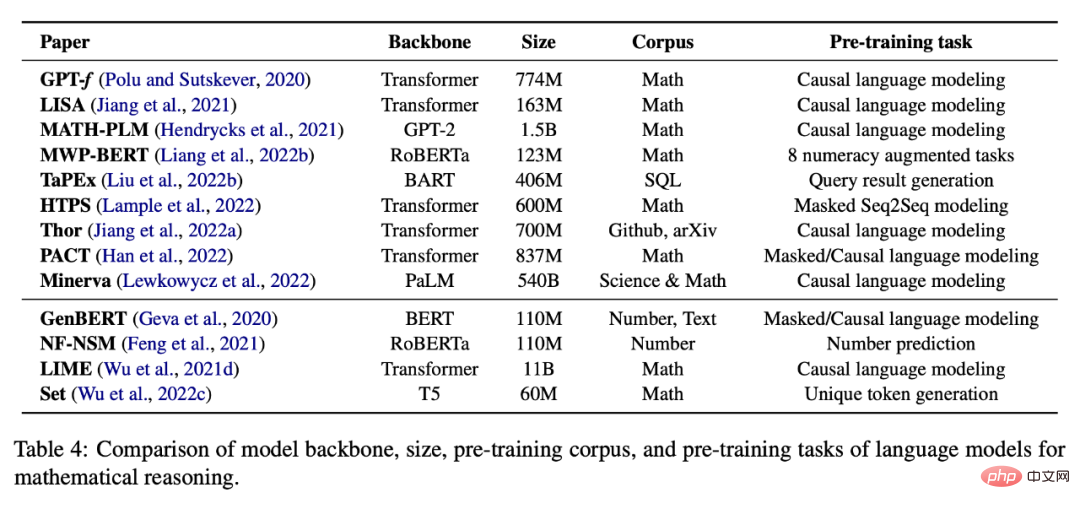
Tabelle 4 unten enthält eine Liste von Sprachmodellen, die für selbstüberwachte Aufgaben des mathematischen Denkens vorab trainiert wurden. Eine aufgabenspezifische Feinabstimmung ist auch eine gängige Praxis, wenn nicht genügend Daten vorhanden sind, um ein großes Modell von Grund auf zu trainieren. Wie in Tabelle 5 dargestellt, wird in bestehenden Arbeiten versucht, vorab trainierte Sprachmodelle für verschiedene nachgelagerte Aufgaben zu optimieren.

Zusätzlich zur Feinabstimmung der Modellparameter verwenden viele Arbeiten auch vorab trainierte Sprachmodelle als Encoder und kombinieren sie mit anderen Modulen, um nachgelagerte Aufgaben zu erledigen. IconQA schlägt beispielsweise vor, ResNet und BERT für die Diagrammerkennung bzw. das Textverständnis zu verwenden .

Kontextuelles Lernen im mathematischen Denken

Ein Beispiel eines Kontexts enthält normalerweise ein Eingabe-Ausgabe-Paar und einige Aufforderungswörter. Wählen Sie beispielsweise die größte Zahl aus der Liste aus.

Eingabe: [2, 4, 1, 5, 8]

Ausgabe: 8.

Few-Shot-Learning liefert mehrere Stichproben, und dann sagt das Modell die Ausgabe für die letzte Eingabestichprobe voraus. Diese Standard-Eingabeaufforderung mit wenigen Schüssen, die große Sprachmodelle mit kontextbezogenen Stichproben von Eingabe-Ausgabe-Paaren vor Stichproben zur Testzeit versorgt, hat sich jedoch nicht als ausreichend erwiesen, um bei anspruchsvollen Aufgaben wie dem mathematischen Denken eine gute Leistung zu erzielen.

Chain-of-Thought Prompting (CoT) verwendet die Zwischenerklärung in natürlicher Sprache als Eingabeaufforderung, sodass das große Sprachmodell zunächst eine Argumentationskette generieren und dann die Antwort auf eine Eingabefrage vorhersagen kann. Beispielsweise kann eine CoT-Eingabeaufforderung zur Lösung von Anwendungsproblemen

Kojima et al. (2022) vorgeschlagen werden, um das Modell mit der Eingabeaufforderung „Machen Sie große Sprachmodelle zu guten Zero-Shots“ zu versehen Denker. Darüber hinaus konzentrierten sich die jüngsten Arbeiten auf die Frage, wie das Denken in der Denkkette im Rahmen der Zero-Shot-Inferenz verbessert werden kann. Diese Art von Arbeit gliedert sich hauptsächlich in zwei Teile: (i) Auswahl besserer kontextbezogener Stichproben und (ii) Erstellung besserer Inferenzketten.

Kontextbezogene Stichprobenauswahl

Die frühe Gedankenkettenarbeit bestand darin, kontextbezogene Stichproben zufällig oder heuristisch auszuwählen. Jüngste Untersuchungen haben gezeigt, dass diese Art des Lernens mit wenigen Schüssen bei unterschiedlicher Auswahl kontextueller Beispiele sehr instabil sein kann. Daher ist es in akademischen Kreisen immer noch ein unbekanntes Thema, welche kontextbezogenen Argumentationsbeispiele die effizientesten Eingabeaufforderungen liefern können.

Um diese Einschränkung zu beheben, haben einige neuere Arbeiten verschiedene Methoden zur Optimierung des Auswahlprozesses für Kontextproben untersucht. Rubin et al. (2022) versuchten beispielsweise, dieses Problem durch den Abruf semantisch ähnlicher Stichproben zu lösen. Dieser Ansatz eignet sich jedoch nicht gut für Probleme des mathematischen Denkens und es ist schwierig, die Ähnlichkeit zu messen, wenn strukturierte Informationen (z. B. Tabellen) enthalten sind. Darüber hinaus schlugen Fu et al. (2022) eine komplexitätsbasierte Eingabeaufforderung vor, bei der Proben mit komplexen Argumentationsketten (d. h. Ketten mit mehr Argumentationsschritten) als Eingabeaufforderungen ausgewählt wurden. Lu et al. (2022b) schlugen eine Methode zur Auswahl kontextbezogener Stichproben durch verstärkendes Lernen vor. Konkret lernt der Agent, aus einem Pool von Kandidaten die beste kontextbezogene Stichprobe zu finden, mit dem Ziel, die vorhergesagte Belohnung für eine bestimmte Trainingsstichprobe bei der Interaktion mit der GPT-3-Umgebung zu maximieren. Darüber hinaus fanden Zhang et al. (2022b) heraus, dass die Diversifizierung von Beispielproblemen auch die Modellleistung verbessern kann. Sie schlugen einen zweistufigen Ansatz vor, um Beispielprobleme im Kontext zu konstruieren: Erstens: Teilen Sie die Probleme eines bestimmten Datensatzes in mehrere Gruppen auf. Zweitens: Wählen Sie aus jeder Gruppe ein repräsentatives Problem aus und verwenden Sie die Zero-Shot-Denkkette einer einfachen Heuristik, um ihre Argumentationskette zu generieren .

Hochwertige Argumentationskette​

Frühe Denkkettenarbeit stützte sich hauptsächlich auf eine einzelne, von Menschen kommentierte Argumentationskette als Eingabeaufforderung. Das manuelle Erstellen von Argumentationsketten hat jedoch zwei Nachteile: Erstens reichen aktuelle Modelle mit zunehmender Komplexität der Aufgaben möglicherweise nicht aus, um zu lernen, alle erforderlichen Argumentationsschritte durchzuführen, und können zweitens nicht einfach auf verschiedene Aufgaben übertragen werden wird leicht durch fehlerhafte Argumentationsschritte beeinflusst, was zu falschen Vorhersagen in der endgültigen Antwort führt. Um dieser Einschränkung zu begegnen, konzentrierte sich die neuere Forschung hauptsächlich auf zwei Aspekte: (i) die manuelle Erstellung komplexerer Beispiele, die als prozessbasierte Methoden bekannt sind, (ii) die Verwendung von Ensemble-ähnlichen Methoden, die als ergebnisbasierte Methoden bekannt sind.

Nach der Evaluierung bestehender Benchmarks und Methoden diskutieren die Autoren auch zukünftige Forschungsrichtungen in diesem Bereich. Weitere Forschungsdetails finden Sie im Originalpapier.

Das obige ist der detaillierte Inhalt vonDie Zahl der Arbeiten ist in den letzten zehn Jahren stark gestiegen. Wie öffnet Deep Learning langsam die Tür zum mathematischen Denken?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!