Die Distanzmetrik ist die Grundlage für überwachte und unbeaufsichtigte Lernalgorithmen, einschließlich k-Nearest Neighbor, Support Vector Machine und K-Means-Clustering usw.
Die Wahl der Distanzmetrik beeinflusst unsere Ergebnisse des maschinellen Lernens, daher ist es wichtig zu überlegen, welche Metrik für das Problem am besten geeignet ist. Daher sollten wir bei der Entscheidung, welche Messmethode wir verwenden, vorsichtig sein. Doch bevor wir eine Entscheidung treffen, müssen wir verstehen, wie die Entfernungsmessung funktioniert und aus welchen Messungen wir wählen können.
In diesem Artikel werden häufig verwendete Methoden zur Entfernungsmessung kurz vorgestellt, wie sie funktionieren, wie sie in Python berechnet werden und wann sie verwendet werden. Dies führt zu tieferem Wissen und Verständnis sowie zu verbesserten Algorithmen und Ergebnissen für maschinelles Lernen.
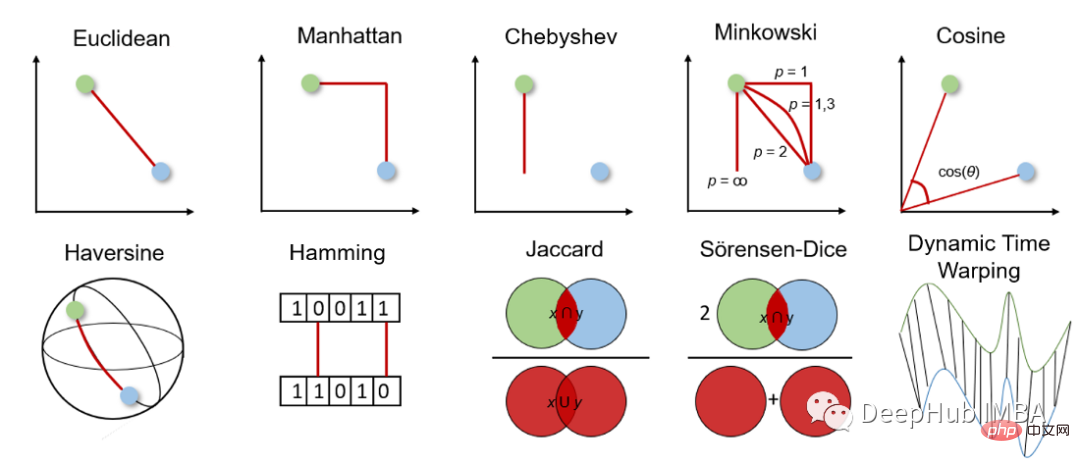
Bevor wir tiefer auf die verschiedenen Distanzmessungen eingehen, wollen wir uns zunächst einen allgemeinen Überblick über ihre Funktionsweise verschaffen und wie man die passende Messung auswählt.
Die Distanzmetrik wird verwendet, um die Differenz zwischen zwei Objekten in einem bestimmten Problemraum, d. h. Features im Datensatz, zu berechnen. Dieser Abstand kann dann verwendet werden, um die Ähnlichkeit zwischen Merkmalen zu bestimmen. Je kleiner der Abstand, desto ähnlicher sind die Merkmale.
Bei der Distanzmessung können wir zwischen geometrischer Distanzmessung und statistischer Distanzmessung wählen. Welche Distanzmessung gewählt werden soll, hängt von der Art der Daten ab. Features können von unterschiedlichen Datentypen sein (z. B. reale Werte, boolesche Werte, kategoriale Werte) und die Daten können mehrdimensional sein oder aus Geodaten bestehen.
Der euklidische Abstand kann auch als l2-Norm bezeichnet werden. Die Berechnungsmethode lautet:
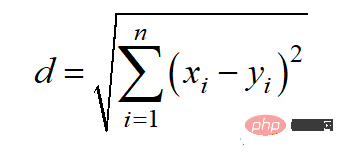Der Python-Code lautet wie folgt:
from scipy.spatial import distance distance.euclidean(vector_1, vector_2)
Der euklidische Abstand hat zwei Hauptnachteile. Erstens funktionieren Entfernungsmessungen nicht mit Daten größerer Dimensionen als dem 2D- oder 3D-Raum. Zweitens können Abstände um Einheiten verzerrt sein, wenn wir die Merkmale nicht normalisieren und/oder normalisieren.
2. Manhattan-Entfernung
Der Manhattan-Abstand basiert auf der l1-Norm und die Berechnungsformel lautet:
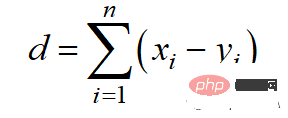Der Python-Code lautet wie folgt:
from scipy.spatial import distance distance.cityblock(vector_1, vector_2)
Der Manhattan-Abstand hat zwei Hauptnachteile. Sie ist nicht so intuitiv wie die euklidische Distanz im hochdimensionalen Raum und zeigt auch nicht den kürzestmöglichen Weg. Obwohl dies möglicherweise kein Problem darstellt, sollten wir uns darüber im Klaren sein, dass dies nicht die kürzeste Entfernung ist.
3. Tschebyscheff-Distanz Tschebyscheff-Distanz
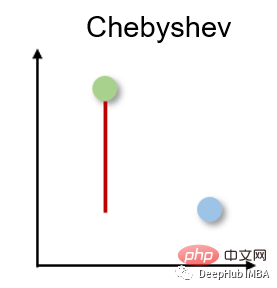Die Chebyshev-Distanz wird nach der L-Unendlichkeitsnorm berechnet:
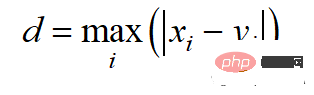Der Python-Code lautet wie folgt:
from scipy.spatial import distance distance.chebyshev(vector_1, vector_2)
Die Chebyshev-Distanz hat nur sehr spezifische Anwendungsfälle und wird daher selten verwendet.
4. Minkowski-Distanz Minkowski-Distanz
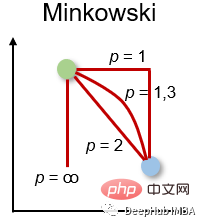Die Berechnungsmethode für den Minkowski-Abstand lautet:
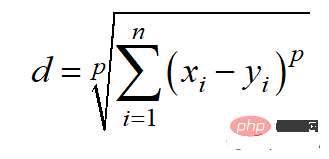Der Python-Code lautet wie folgt:
from scipy.spatial import distance distance.minkowski(vector_1, vector_2, p)
Da der Minkowski-Abstand unterschiedliche Abstandsmaße darstellt, weist er die gleichen Hauptnachteile auf wie diese, z. B. Probleme mit großen Dimensionen mit Raum und Abhängigkeit von charakteristischen Einheiten. Darüber hinaus kann die Flexibilität von p-Werten auch ein Nachteil sein, da sie die Recheneffizienz verringern kann, da mehrere Berechnungen erforderlich sind, um den richtigen p-Wert zu ermitteln.
5. Kosinusähnlichkeit und Abstand Kosinusähnlichkeit
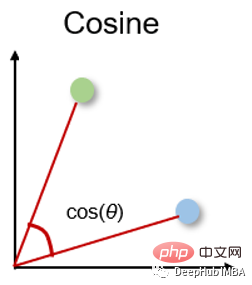
余弦相似度可以介于-1(相反方向)和1(相同方向)之间，计算方法为:
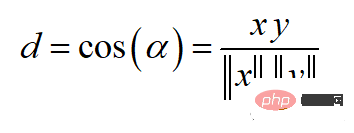
余弦相似度常用于范围在0到1之间的正空间中。余弦距离就是用1减去余弦相似度，位于0(相似值)和1(不同值)之间。
Python代码如下
from scipy.spatial import distance distance.cosine(vector_1, vector_2)
余弦距离的主要缺点是它不考虑大小而只考虑向量的方向。因此，没有充分考虑到值的差异。
半正矢距离测量的是球面上两点之间的最短距离。因此常用于导航，其中经度和纬度和曲率对计算都有影响。
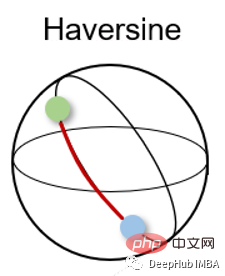
半正矢距离的公式如下：
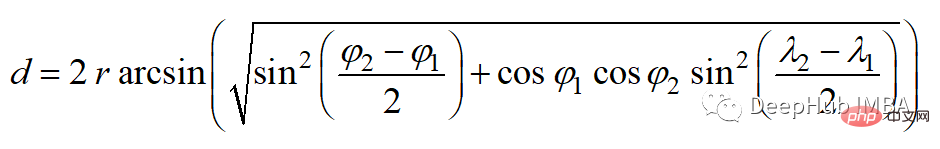
其中r为球面半径，φ和λ为经度和纬度。
Python代码如下
from sklearn.metrics.pairwise import haversine_distances haversine_distances([vector_1, vector_2])
半正矢距离的主要缺点是假设是一个球体，而这种情况很少出现。
汉明距离衡量两个二进制向量或字符串之间的差异。
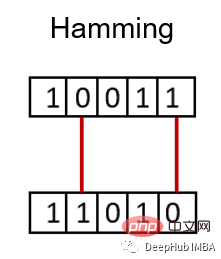
对向量按元素进行比较，并对差异的数量进行平均。如果两个向量相同，得到的距离是0之间，如果两个向量完全不同，得到的距离是1。
Python代码如下
from scipy.spatial import distance distance.hamming(vector_1, vector_2)
汉明距离有两个主要缺点。距离测量只能比较相同长度的向量，它不能给出差异的大小。所以当差异的大小很重要时，不建议使用汉明距离。
统计距离测量可用于假设检验、拟合优度检验、分类任务或异常值检测。
Jaccard指数用于确定两个样本集之间的相似性。它反映了与整个数据集相比存在多少一对一匹配。Jaccard指数通常用于二进制数据比如图像识别的深度学习模型的预测与标记数据进行比较，或者根据单词的重叠来比较文档中的文本模式。
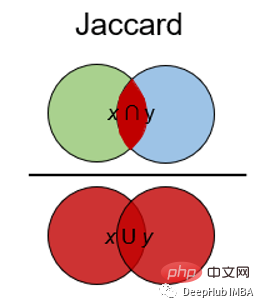
Jaccard距离的计算方法为:
Python代码如下
from scipy.spatial import distance distance.jaccard(vector_1, vector_2)
Jaccard指数和距离的主要缺点是，它受到数据规模的强烈影响，即每个项目的权重与数据集的规模成反比。
Sörensen-Dice指数类似于Jaccard指数，它可以衡量的是样本集的相似性和多样性。该指数更直观，因为它计算重叠的百分比。Sörensen-Dice索引常用于图像分割和文本相似度分析。
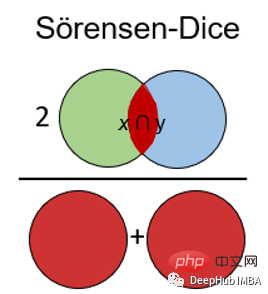
计算公式如下：
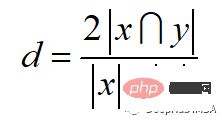
Python代码如下
from scipy.spatial import distance distance.dice(vector_1, vector_2)
它的主要缺点也是受数据集大小的影响很大。
动态时间规整是测量两个不同长度时间序列之间距离的一种重要方法。可以用于所有时间序列数据的用例，如语音识别或异常检测。
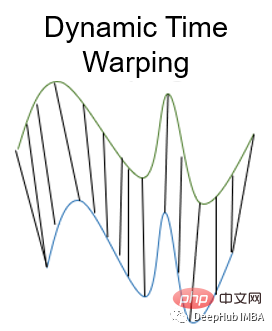
为什么我们需要一个为时间序列进行距离测量的度量呢？如果时间序列长度不同或失真，则上述面说到的其他距离测量无法确定良好的相似性。比如欧几里得距离计算每个时间步长的两个时间序列之间的距离。但是如果两个时间序列的形状相同但在时间上发生了偏移，那么尽管时间序列非常相似，但欧几里得距离会表现出很大的差异。
动态时间规整通过使用多对一或一对多映射来最小化两个时间序列之间的总距离来避免这个问题。当搜索最佳对齐时，这会产生更直观的相似性度量。通过动态规划找到一条弯曲的路径最小化距离，该路径必须满足以下条件：
我们可以使用 Python 中的 fastdtw 包：
from scipy.spatial.distance import euclidean from fastdtw import fastdtw distance, path = fastdtw(timeseries_1, timeseries_2, dist=euclidean)
动态时间规整的一个主要缺点是与其他距离测量方法相比，它的计算工作量相对较高。
在这篇文章中，简要介绍了十种常用的距离测量方法。本文中已经展示了它们是如何工作的，如何在Python中实现它们，以及经常使用它们解决什么问题。如果你认为我错过了一个重要的距离测量，请留言告诉我。
Das obige ist der detaillierte Inhalt vonZehn häufig verwendete Entfernungsmessmethoden beim maschinellen Lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
