Quantenalgorithmen lösen ein neuartiges Problem!
1994 fand ein Mathematiker heraus, wie man Quantencomputer dazu bringen kann, Dinge zu tun, die gewöhnliche klassische Computer nicht können. Die Arbeit zeigt, dass eine Maschine, die auf den Regeln der Quantenmechanik basiert, im Prinzip große Zahlen effizient in ihre Hauptfaktoren zerlegen kann – eine sehr schwierige Aufgabe für klassische Computer, die die meisten heutigen Grundlagen der Internetsicherheit ausmachen.
Damit kam eine Welle des Optimismus. Vielleicht, so glauben Forscher, gelingt es uns, Quantenalgorithmen zu erfinden, die eine Vielzahl unterschiedlicher Probleme lösen können.
Aber der Fortschritt kam zum Stillstand. „Es ist irgendwie enttäuschend“, sagte Ryan O'Donnell von der Carnegie Mellon University. „Die Leute werden sagen: ‚Das ist großartig, ich bin sicher, wir werden alle möglichen anderen erstaunlichen Algorithmen bekommen‘, und das sind sie auch.“ nicht.“ Die Wissenschaftler fanden nur signifikante Beschleunigungen für eine einzige, enge Klasse von Problemen in einem Standardsatz namens NP, was bedeutet, dass sie über effiziente überprüfbare Lösungen verfügen – wie etwa die Faktorisierung.
Das ist schon seit drei Jahren so. Im April erfanden Forscher dann ein völlig neuartiges Problem, das Quantencomputer schneller lösen können sollten als klassische Computer. Es geht darum, den Input eines komplexen mathematischen Prozesses allein auf der Grundlage seines chaotischen Outputs zu berechnen. Ob dieses Problem ein Einzelfall ist oder das erste von vielen anderen ist, muss noch geklärt werden.
„Da ist ein Gefühl der Aufregung“, sagte Vinod Vaikuntanathan, ein Informatiker am MIT. Da ist nichts.“
Informatiker versuchen besser zu verstehen, was Quantencomputer können, indem sie mathematische Modelle untersuchen, die sie darstellen. Typischerweise stellen sie sich ein Modell eines Quantencomputers oder eines klassischen Computers vor, gepaart mit einem idealen Computer namens Orakel. Ein Orakel ist wie eine einfache mathematische Funktion oder ein Computerprogramm, das Eingaben entgegennimmt und eine vorgegebene Ausgabe ausgibt.
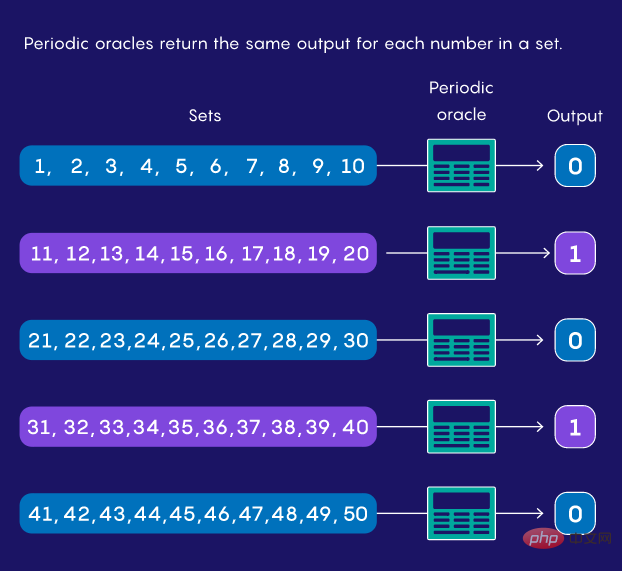
Sie können ein zufälliges Verhalten aufweisen und „Ja“ ausgeben, wenn die Eingabe in einem zufälligen Bereich liegt (z. B. 12 bis 67). Andernfalls geben Sie „Nein“ aus. Oder sie könnten periodisch sein, so dass eine Eingabe zwischen 1 und 10 „Ja“ zurückgibt, 11 bis 20 „Nein“ ergibt, 21 bis 30 wiederum „Ja“ ergibt und so weiter.
Angenommen, Sie haben eine dieser periodischen Prophezeiungen, kennen aber den Zeitraum nicht. Alles, was Sie tun können, ist, ihm Zahlen zu geben und zu sehen, was er ausgibt. Wie schnell kann ein Computer unter diesen Einschränkungen Zyklen finden? Im Jahr 1993 entdeckte Daniel Simon, damals an der Universität Montreal, dass Quantenalgorithmen Antworten auf eng verwandte Probleme schneller berechnen konnten als jeder klassische Algorithmus. Dieses Ergebnis ermöglicht es Simon festzustellen, wo Quantencomputer ein erhebliches Potenzial haben. Eines der ersten Anzeichen einer Dominanz. Doch als er sein Papier bei einer großen Konferenz einreichte, wurde es abgelehnt. Das Papier weckte jedoch das Interesse eines jüngeren Mitglieds des Konferenzprogrammkomitees, Peter Shor, der damals bei Bell Laboratories in New Jersey arbeitete.
Shors Ergebnisse waren historisch. Der von ihm entdeckte Quantenalgorithmus kann große Zahlen schnell auf ihre Primfaktoren reduzieren, was kein bekannter klassischer Algorithmus kann. In den Folgejahren entdeckten Forscher weitere effiziente Quantenalgorithmen. Einige von ihnen, wie Shors Algorithmus, bieten sogar exponentielle Vorteile, aber niemand konnte einen signifikanten Quantenvorteil bei einem nichtperiodischen NP-Problem nachweisen.
Aufgrund mangelnder Fortschritte haben zwei Informatiker, Scott Aaronson von der University of Texas in Austin und Andris Ambainis von der University von Lettland, durchgeführte Beobachtung. Beweise für den Quantenvorteil scheinen immer auf Vorhersagen mit einer nicht zufälligen Struktur, wie etwa der Periodizität, zu beruhen. Im Jahr 2009 spekulierten sie, dass es bei zufälligen oder unstrukturierten NP-Problemen keine nennenswerte Beschleunigung geben würde;
Ihre Vermutung schränkt die Fähigkeiten von Quantencomputern ein. Aber es heißt nur, dass es für bestimmte Arten von unstrukturierten NP-Problemen – solche mit Ja- oder Nein-Antworten – keine signifikante Beschleunigung gibt. Diese Vermutung gilt nicht, wenn es bei einem Problem darum geht, eine spezifischere, quantitative Antwort zu finden, ein sogenanntes Suchproblem. Vor diesem Hintergrund beschlossen die Forscher Takashi Yamakawa vom NTT Social Informatics Laboratory und Mark Zhandry von NTT Research und der Princeton University, 2005 mit einem spezifischen Suchproblem zu experimentieren, das Oded Regev gestellt hatte. Stellen Sie sich eine Reihe von Wetterfahnen vor, die alle in die gleiche Richtung zeigen. Geben Sie ihnen jeweils einen maßvollen Stoß und lassen Sie die Böe ihre Richtung beeinflussen. Regev möchte anhand ihrer endgültigen Richtung feststellen, wohin sie ursprünglich gerichtet waren. Probleme wie dieses wurden als „Fehlerlernen“ bekannt, da Schub und Wind als zufällige Fehlerquellen in der ursprünglichen Richtung wirken. Es gibt Hinweise darauf, dass sowohl klassische als auch Quantenalgorithmen schwer zu lösen sind. Yamakawa und Zhandry haben die Einstellungen optimiert. Sie haben die Stärke dieser Starts verändert, um sie vorhersehbarer zu machen. Sie haben auch dafür gesorgt, dass der Wind durch ein zufälliges Orakel bestimmt wird, sodass er in einigen Fällen noch zufälliger ist, in anderen Fällen jedoch völlig inaktiv ist. Mit diesen Modifikationen fanden die Forscher heraus, dass der Quantenalgorithmus effektiv die ursprüngliche Richtung finden kann. Sie bewiesen auch, dass jeder klassische Algorithmus um einen exponentiellen Faktor verlangsamt werden muss. Wie Shor passten sie dann den Algorithmus an, um eine realistische Version des Problems zu lösen, indem sie die Vorhersagen durch tatsächliche mathematische Gleichungen ersetzten. Informatiker versuchen immer noch, dieses Problem zu verstehen und zu lösen. Vaikuntanathan verglich dies mit einer anderen Situation, die bei der Datenkomprimierung auftritt: Wenn Informationen komprimiert werden, können zwei Bits versehentlich an die gleiche Stelle gequetscht und so überschrieben werden. Die Probleme, diese Kollisionen im Voraus zu antizipieren, um sie zu vermeiden, weisen einige Ähnlichkeiten auf. „Das ist eine Klasse von Problemen, die im Grunde so aussehen“, sagte er. „Vielleicht können diese Probleme auch auf den heutigen jungen Versionen von Quantencomputern gelöst werden.“ gelöst und bietet eine Möglichkeit, sie zu testen. Die Idee war, dass unstrukturierte Probleme möglicherweise weniger Ressourcen zum Programmieren erfordern oder weniger empfindlich gegenüber Rauschen sind, weil sie bereits zufällig sind. Bisher scheint dieses neue Problem jedoch noch zu weit fortgeschritten zu sein, als dass bestehende Quantencomputer es lösen könnten. „Es ist ein seltsames Problem. Ich habe nicht darüber nachgedacht, es zu definieren“, sagte Aaronson, „aber im Nachhinein betrachtet hat es einige wirklich nette Eigenschaften.“ Beispiele für signifikante Quantenvorteile bei NP-basierten Problemen.“ Werden viele andere Probleme in der Quantenwelt von nahezu unlösbar zu lösbar werden? Jetzt gibt es noch mehr Gründe zu dieser Annahme. „Dies verändert in gewissem Maße unsere Sicht darauf, welche Probleme Quantencomputer gut lösen können“, sagte O’Donnell.
Das obige ist der detaillierte Inhalt vonQuantenalgorithmen lösen ein neuartiges Problem!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 CUDAs universelle Matrixmultiplikation: vom Einstieg bis zur Kompetenz!
Mar 25, 2024 pm 12:30 PM
CUDAs universelle Matrixmultiplikation: vom Einstieg bis zur Kompetenz!
Mar 25, 2024 pm 12:30 PM
Die allgemeine Matrixmultiplikation (GEMM) ist ein wesentlicher Bestandteil vieler Anwendungen und Algorithmen und außerdem einer der wichtigen Indikatoren zur Bewertung der Leistung der Computerhardware. Eingehende Forschung und Optimierung der Implementierung von GEMM können uns helfen, Hochleistungsrechnen und die Beziehung zwischen Software- und Hardwaresystemen besser zu verstehen. In der Informatik kann eine effektive Optimierung von GEMM die Rechengeschwindigkeit erhöhen und Ressourcen einsparen, was für die Verbesserung der Gesamtleistung eines Computersystems von entscheidender Bedeutung ist. Ein tiefgreifendes Verständnis des Funktionsprinzips und der Optimierungsmethode von GEMM wird uns helfen, das Potenzial moderner Computerhardware besser zu nutzen und effizientere Lösungen für verschiedene komplexe Computeraufgaben bereitzustellen. Durch Optimierung der Leistung von GEMM
 So berechnen Sie Addition, Subtraktion, Multiplikation und Division in einem Word-Dokument
Mar 19, 2024 pm 08:13 PM
So berechnen Sie Addition, Subtraktion, Multiplikation und Division in einem Word-Dokument
Mar 19, 2024 pm 08:13 PM
WORD ist ein leistungsstarkes Textverarbeitungsprogramm, mit dem wir verschiedene Texte in Excel bearbeiten können. Wir beherrschen die Berechnungsmethoden der Addition, Subtraktion und Multiplikatoren. Wie subtrahiere ich den Multiplikator? Kann ich ihn nur mit einem Taschenrechner berechnen? Die Antwort ist natürlich nein, WORD kann das auch. Heute werde ich Ihnen beibringen, wie Sie mit Formeln grundlegende Operationen wie Addition, Subtraktion, Multiplikation und Division in Tabellen in Word-Dokumenten berechnen. Lassen Sie mich heute im Detail zeigen, wie man Addition, Subtraktion, Multiplikation und Division in einem WORD-Dokument berechnet. Schritt 1: Öffnen Sie ein WORD, klicken Sie in der Symbolleiste unter [Einfügen] auf [Tabelle] und fügen Sie eine Tabelle in das Dropdown-Menü ein.
 So zählen Sie die Anzahl der Elemente in einer Liste mit der Funktion count() von Python
Nov 18, 2023 pm 02:53 PM
So zählen Sie die Anzahl der Elemente in einer Liste mit der Funktion count() von Python
Nov 18, 2023 pm 02:53 PM
Um die Anzahl der Elemente in einer Liste mit der Funktion count() von Python zu zählen, sind bestimmte Codebeispiele erforderlich. Als leistungsstarke und leicht zu erlernende Programmiersprache bietet Python viele integrierte Funktionen zur Verarbeitung unterschiedlicher Datenstrukturen. Eine davon ist die Funktion count(), mit der sich die Anzahl der Elemente in einer Liste zählen lässt. In diesem Artikel erklären wir die Verwendung der count()-Funktion im Detail und stellen spezifische Codebeispiele bereit. Die Funktion count() ist eine in Python integrierte Funktion, mit der ein bestimmter Wert berechnet wird
 Java-Programm zur Berechnung der Fläche eines Dreiecks mithilfe von Determinanten
Aug 31, 2023 am 10:17 AM
Java-Programm zur Berechnung der Fläche eines Dreiecks mithilfe von Determinanten
Aug 31, 2023 am 10:17 AM
Einführung Das Java-Programm zur Berechnung der Fläche eines Dreiecks mithilfe der Determinante ist ein prägnantes und effizientes Programm, das die Fläche eines Dreiecks anhand der Koordinaten von drei Eckpunkten berechnen kann. Dieses Programm ist für jeden nützlich, der Geometrie erlernt oder damit arbeitet, da es zeigt, wie man grundlegende arithmetische und algebraische Berechnungen in Java verwendet und wie man die Scanner-Klasse zum Lesen von Benutzereingaben verwendet. Das Programm fordert den Benutzer zur Eingabe der Koordinaten von drei Punkten des Dreiecks auf, die dann eingelesen und zur Berechnung der Determinante der Koordinatenmatrix verwendet werden. Verwenden Sie den Absolutwert der Determinante, um sicherzustellen, dass die Fläche immer positiv ist. Verwenden Sie dann eine Formel, um die Fläche des Dreiecks zu berechnen und sie dem Benutzer anzuzeigen. Das Programm kann leicht modifiziert werden, um Eingaben in verschiedenen Formaten zu akzeptieren oder zusätzliche Berechnungen durchzuführen, was es zu einem vielseitigen Werkzeug für geometrische Berechnungen macht. Reihen von Determinanten
 Zählen Sie rekursiv die Anzahl der Vorkommen eines Teilstrings in Java
Sep 17, 2023 pm 07:49 PM
Zählen Sie rekursiv die Anzahl der Vorkommen eines Teilstrings in Java
Sep 17, 2023 pm 07:49 PM
Gegeben seien zwei Strings str_1 und str_2. Das Ziel besteht darin, mithilfe eines rekursiven Verfahrens die Anzahl der Vorkommen der Teilzeichenfolge str2 in der Zeichenfolge str1 zu zählen. Eine rekursive Funktion ist eine Funktion, die sich innerhalb ihrer Definition selbst aufruft. Wenn str1 „Iknowthatyouknowthatiknow“ und str2 „know“ ist, beträgt die Anzahl der Vorkommen -3. Lassen Sie uns das anhand von Beispielen verstehen. Geben Sie beispielsweise str1="TPisTPareTPamTP", str2="TP" ein; geben Sie Countofoccurrencesofasubstringrecursi aus
 So verwenden Sie die Math.Pow-Funktion in C#, um die Potenz einer bestimmten Zahl zu berechnen
Nov 18, 2023 am 11:32 AM
So verwenden Sie die Math.Pow-Funktion in C#, um die Potenz einer bestimmten Zahl zu berechnen
Nov 18, 2023 am 11:32 AM
In C# gibt es eine Math-Klassenbibliothek, die viele mathematische Funktionen enthält. Dazu gehört die Funktion Math.Pow, die Potenzen berechnet und uns dabei helfen kann, die Potenz einer bestimmten Zahl zu berechnen. Die Verwendung der Math.Pow-Funktion ist sehr einfach, Sie müssen lediglich die Basis und den Exponenten angeben. Die Syntax lautet wie folgt: Math.Pow(base,exponent); wobei base die Basis und exponent den Exponenten darstellt. Diese Funktion gibt ein Ergebnis vom Typ Double zurück, nämlich das Ergebnis der Leistungsberechnung. Lasst uns
 Python-Programm zur Berechnung der Summe der rechtsdiagonalen Elemente einer Matrix
Aug 19, 2023 am 11:29 AM
Python-Programm zur Berechnung der Summe der rechtsdiagonalen Elemente einer Matrix
Aug 19, 2023 am 11:29 AM
Eine beliebte Allzweck-Programmiersprache ist Python. Es wird in einer Vielzahl von Branchen eingesetzt, darunter Desktop-Anwendungen, Webentwicklung und maschinelles Lernen. Glücklicherweise verfügt Python über eine einfache und leicht verständliche Syntax, die für Anfänger geeignet ist. In diesem Artikel verwenden wir Python, um die Summe der rechten Diagonalen einer Matrix zu berechnen. Was ist eine Matrix? In der Mathematik verwenden wir ein rechteckiges Array oder eine Matrix, um ein mathematisches Objekt oder seine Eigenschaften zu beschreiben. Es handelt sich um ein rechteckiges Array oder eine Tabelle, die in Zeilen und Spalten angeordnete Zahlen, Symbole oder Ausdrücke enthält. Zum Beispiel -234512367574. Dies ist also eine Matrix mit 3 Zeilen und 4 Spalten, ausgedrückt als 3*4-Matrix. Nun gibt es in der Matrix zwei Diagonalen, die Primärdiagonale und die Sekundärdiagonale
 Java-Programmbeispiel zur Berechnung der Gesamtpunktzahl und des Prozentsatzes
Sep 11, 2023 pm 06:01 PM
Java-Programmbeispiel zur Berechnung der Gesamtpunktzahl und des Prozentsatzes
Sep 11, 2023 pm 06:01 PM
Wir zeigen Ihnen, wie Sie mit einem Java-Programm Gesamtpunktzahlen und Prozentsätze berechnen. Die Gesamtpunktzahl bezieht sich auf die Summe aller verfügbaren Punktzahlen, während sich der Begriff „Prozentsatz“ auf die berechnete Punktzahl bezieht, geteilt durch die Gesamtpunktzahl und multipliziert mit der resultierenden Zahl 100. „percentage_of_marks=(obtained_marks/total_marks)×100 Beispiel 1“ Dies ist ein Java-Programm, das zeigt, wie Gesamtpunktzahlen und Prozentsätze berechnet werden. //JavaProgramtodemonstratehowisTotalmarksandPercentagescalculatedimportjava.io.*;publicclassTotalMarks_




