Lernen = passend? Sind Deep Learning und klassische Statistik dasselbe?

​In diesem Artikel vergleicht Boaz Barak, ein theoretischer Informatiker und bekannter Professor an der Harvard University, die Unterschiede zwischen Deep Learning und klassischer Statistik im Detail. Er ist davon überzeugt, dass „wenn man Deep Learning rein aus statistischer Sicht versteht, man wird die Schlüsselfaktoren für seinen Erfolg ignorieren.

Deep Learning (oder maschinelles Lernen im Allgemeinen) wird oft einfach als Statistik betrachtet, d. h. es handelt sich im Grunde um dasselbe Konzept, das Statistiker studieren, es wird jedoch mit einer anderen Terminologie als Statistik beschrieben. Rob Tibshirani hat dieses interessante „Vokabular“ einmal unten zusammengefasst:

Kommt etwas in dieser Liste wirklich in Resonanz? Praktisch jeder, der sich mit maschinellem Lernen beschäftigt, weiß, dass viele der Begriffe auf der rechten Seite der von Tibshiriani geposteten Tabelle im maschinellen Lernen weit verbreitet sind.

Wenn Sie Deep Learning rein aus statistischer Sicht verstehen, werden Sie die Schlüsselfaktoren für seinen Erfolg außer Acht lassen. Eine angemessenere Beurteilung von Deep Learning besteht darin, dass es statistische Begriffe verwendet, um völlig unterschiedliche Konzepte zu beschreiben.

Die richtige Beurteilung von Deep Learning besteht nicht darin, dass es andere Wörter verwendet, um alte statistische Begriffe zu beschreiben, sondern dass es diese Begriffe verwendet, um völlig unterschiedliche Prozesse zu beschreiben.

In diesem Artikel wird erklärt, warum sich die Grundlagen des Deep Learning tatsächlich von der Statistik oder sogar vom klassischen maschinellen Lernen unterscheiden. In diesem Artikel wird zunächst der Unterschied zwischen der „Erklärungs“-Aufgabe und der „Vorhersage“-Aufgabe bei der Anpassung eines Modells an Daten erläutert. Anschließend werden zwei Szenarien des Lernprozesses diskutiert: 1. Anpassung statistischer Modelle mithilfe empirischer Risikominimierung; 2. Vermittlung mathematischer Fähigkeiten an Studierende; Anschließend wird im Artikel erläutert, welches Szenario dem Wesen des Deep Learning näher kommt.

Während die Mathematik und der Code für Deep Learning fast mit der Anpassung statistischer Modelle identisch sind. Aber auf einer tieferen Ebene ähnelt Deep Learning eher der Vermittlung mathematischer Fähigkeiten an Schüler. Und es dürfte nur sehr wenige Menschen geben, die sich trauen zu behaupten: Ich beherrsche die komplette Deep-Learning-Theorie! Tatsächlich ist es zweifelhaft, ob eine solche Theorie existiert. Stattdessen lassen sich verschiedene Aspekte des Deep Learning am besten aus unterschiedlichen Perspektiven verstehen, und Statistiken allein können kein vollständiges Bild liefern.

Dieser Artikel vergleicht Deep Learning und Statistik und bezieht sich hier speziell auf „klassische Statistik“, da sie am längsten untersucht wurde und schon lange in Lehrbüchern steht. Viele Statistiker arbeiten an Deep Learning und nichtklassischen theoretischen Methoden, so wie die Physiker des 20. Jahrhunderts den Rahmen der klassischen Physik erweitern mussten. Tatsächlich kommt es beiden Seiten zugute, wenn die Grenzen zwischen Informatikern und Statistikern verwischt werden.

Vorhersage und Modellanpassung

Wissenschaftler haben immer Modellberechnungsergebnisse mit tatsächlichen Beobachtungsergebnissen verglichen, um die Genauigkeit des Modells zu überprüfen. Der ägyptische Astronom Ptolemaios schlug ein geniales Modell der Planetenbewegung vor. Das Modell von Ptolemäus folgte dem Geozentrismus, verfügte jedoch über eine Reihe von Epizykeln (siehe Abbildung unten), was ihm eine ausgezeichnete Vorhersagegenauigkeit verlieh. Im Gegensatz dazu war das ursprüngliche heliozentrische Modell von Kopernikus einfacher als das ptolemäische Modell, aber weniger genau bei der Vorhersage von Beobachtungen. (Kopernikus fügte später seine eigenen Epizyklen hinzu, um mit dem Modell von Ptolemäus vergleichbar zu sein.)

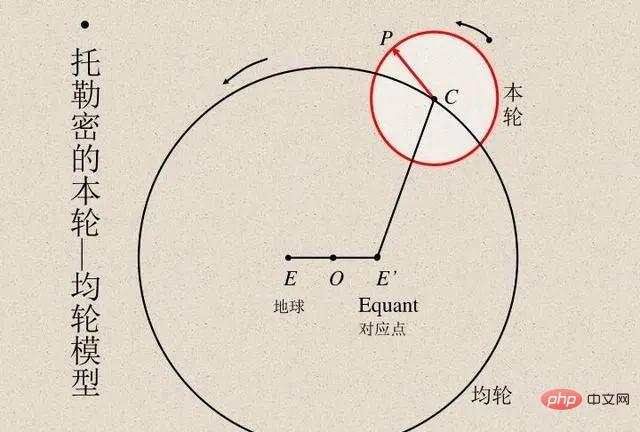
Sowohl die Modelle von Ptolemäus als auch von Kopernikus sind beispiellos. Wenn wir Vorhersagen über eine „Black Box“ treffen wollen, dann ist das geozentrische Modell des Ptolemäus überlegen. Wenn Sie jedoch ein einfaches Modell suchen, mit dem Sie „nach innen schauen“ können (was den Ausgangspunkt für Theorien zur Erklärung der Sternbewegung darstellt), dann ist das Modell von Kopernikus der richtige Weg. Später verbesserte Kepler das Modell von Kopernikus zu einer elliptischen Umlaufbahn und schlug Keplers drei Gesetze der Planetenbewegung vor, die es Newton ermöglichten, die Planetengesetze mit dem auf die Erde anwendbaren Gesetz der Schwerkraft zu erklären.

Daher ist es wichtig, dass das heliozentrische Modell nicht nur eine „Black Box“ ist, die Vorhersagen liefert, sondern durch ein paar einfache mathematische Gleichungen gegeben ist, allerdings mit sehr wenigen „beweglichen Teilen“ in den Gleichungen. Die Astronomie ist seit vielen Jahren eine Inspirationsquelle für die Entwicklung statistischer Techniken. Gauß und Legendre erfanden um 1800 unabhängig voneinander die Regression der kleinsten Quadrate, um die Umlaufbahnen von Asteroiden und anderen Himmelskörpern vorherzusagen. Im Jahr 1847 erfand Cauchy die Gradientenabstiegsmethode, die ebenfalls durch astronomische Vorhersagen motiviert war.

In der Physik verfügen Akademiker manchmal über alle Details, um die „richtige“ Theorie zu finden, die Vorhersagegenauigkeit zu optimieren und die Daten bestmöglich zu interpretieren. Diese liegen im Rahmen von Ideen wie Occams Rasiermesser, bei denen man davon ausgehen kann, dass Einfachheit, Vorhersagekraft und Erklärungskraft alle im Einklang miteinander stehen.

Allerdings ist in vielen anderen Bereichen das Verhältnis zwischen den beiden Zielen Erklärung und Vorhersage nicht so harmonisch. Wenn Sie nur Beobachtungen vorhersagen möchten, ist es wahrscheinlich am besten, durch eine „Black Box“ zu gehen. Möchte man hingegen erklärende Informationen wie Kausalmodelle, allgemeine Prinzipien oder wichtige Merkmale erhalten, gilt: Je einfacher das Modell, das verstanden und erklärt werden kann, desto besser.

Die richtige Wahl des Modells hängt von seinem Verwendungszweck ab. Betrachten Sie beispielsweise einen Datensatz, der die genetische Expression und die Phänotypen vieler Individuen enthält (z. B. eine Krankheit). Wenn das Ziel darin besteht, die Wahrscheinlichkeit einer Erkrankung einer Person vorherzusagen, dann ist es egal, wie komplex es ist oder auf wie vielen Genen es beruht. Verwenden Sie das beste Vorhersagemodell, das an die Aufgabe angepasst ist. Geht es hingegen darum, einige wenige Gene für weitere Untersuchungen zu identifizieren, ist eine komplexe und sehr präzise „Black Box“ von begrenztem Nutzen.

Der Statistiker Leo Breiman hat diesen Punkt in seinem berühmten Artikel „Zwei Kulturen in der statistischen Modellierung“ aus dem Jahr 2001 hervorgehoben. Die erste ist eine „Datenmodellierungskultur“, die sich auf einfache generative Modelle konzentriert, die die Daten erklären können. Die zweite ist eine „algorithmische Modellierungskultur“, die unabhängig davon ist, wie die Daten generiert wurden, und sich darauf konzentriert, Modelle zu finden, die die Daten vorhersagen können, egal wie komplex sie sind. 🔜 , dieser Fokus schafft zwei Probleme:

führt zu irrelevanten Theorien und fragwürdigen wissenschaftlichen Schlussfolgerungen

hindert Statistiker daran, spannende neue Fragen zu untersuchen

Sobald Breimans Artikel herauskam, löste er einige Kontroversen aus. Sein Statistikkollege Brad Efron antwortete, dass er zwar einigen Punkten zustimmte, aber auch betonte, dass Breimans Argumentation offenbar gegen Genügsamkeit und wissenschaftliche Erkenntnisse spricht und dafür, große Anstrengungen zu unternehmen, um komplexe „Black Boxes“ zu schaffen. Doch in einem kürzlich erschienenen Artikel gab Efron seine bisherige Ansicht auf und gab zu, dass Breima vorausschauender sei, weil „der Schwerpunkt der Statistik im 21. Jahrhundert auf Vorhersagealgorithmen liegt, die sich weitgehend entlang der von Breiman vorgeschlagenen Linien entwickelt haben.“

Klassische und moderne Vorhersagemodelle

Maschinelles Lernen, ob Deep Learning oder nicht, hat sich im Sinne von Breimans zweiter Sichtweise entwickelt, die sich auf Vorhersagen konzentriert. Diese Kultur hat eine lange Geschichte. Beispielsweise wurde in dem 1973 veröffentlichten Lehrbuch von Duda und Hart und in der Arbeit von Highleyman aus dem Jahr 1962 über den Inhalt der folgenden Abbildung geschrieben, was für heutige Deep-Learning-Forscher sehr leicht zu verstehen ist:

• Duda und Hart Auszüge aus dem Lehrbuch „Pattern Classification“. und Szenenanalyse“ und Highleymans 1962 erschienene Arbeit „The Design and Analysis of Pattern Recognition Experiments“.
• In ähnlicher Weise wird das Bild unten von Highleymans handgeschriebenem Zeichendatensatz und der dafür verwendeten Architektur, Chow (1962) (Genauigkeit ~58 %), bei vielen Menschen Anklang finden.

Warum ist Deep Learning anders?

Im Jahr 1992 schrieben Geman, Bienenstock und Doursat einen pessimistischen Artikel über neuronale Netze und argumentierten, dass „aktuelle vorwärtsgerichtete neuronale Netze weitgehend unzureichend sind, um schwierige Probleme der maschinellen Wahrnehmung und des maschinellen Lernens zu lösen.“ Konkret argumentieren sie, dass universelle neuronale Netze bei der Bewältigung schwieriger Aufgaben nicht erfolgreich sein werden und dass sie nur durch künstlich gestaltete Funktionen erfolgreich sein können. In ihren Worten: „Die wichtigen Eigenschaften müssen eingebaut oder „fest verdrahtet“ sein … und nicht im statistischen Sinne gelernt.“ Nun scheinen Geman et al. völlig falsch zu liegen, aber es ist interessanter, sie zu verstehen warum sie Unrecht haben.

Deep Learning unterscheidet sich tatsächlich von anderen Lernmethoden. Auch wenn Deep Learning nur wie eine Vorhersage erscheint, wie der nächste Nachbar oder eine zufällige Gesamtstruktur, kann es über komplexere Parameter verfügen. Dies scheint eher ein quantitativer als ein qualitativer Unterschied zu sein. Aber in der Physik ist oft eine völlig andere Theorie erforderlich, sobald sich die Skala um einige Größenordnungen ändert, und das gilt auch für Deep Learning. Die zugrunde liegenden Prozesse von Deep Learning und klassischen Modellen (parametrisch oder nicht parametrisch) sind völlig unterschiedlich, obwohl ihre mathematischen Gleichungen (und der Python-Code) auf hoher Ebene gleich sind.

Um diesen Punkt zu veranschaulichen, betrachten Sie zwei verschiedene Szenarien: die Anpassung eines statistischen Modells und den Mathematikunterricht für Schüler.

Szenario A: Anpassen eines statistischen Modells

Die typischen Schritte zum Anpassen eines statistischen Modells anhand von Daten sind wie folgt:

1. Hier sind einige Daten

(

ist die Matrix von

;

ist der

-dimensionale Vektor, das heißt, die Kategoriebezeichnung. Stellen Sie sich vor, dass die Daten von einem Modell stammen, das Struktur hat und Rauschen enthält, also dem Modell, das angepasst werden soll)

2. Verwenden Sie die oben genannten Daten, um ein Modell anzupassen und verwenden Sie einen Optimierungsalgorithmus, um das empirische Risiko zu minimieren. Das heißt, durch den Optimierungsalgorithmus finden wir ein solches , sodass 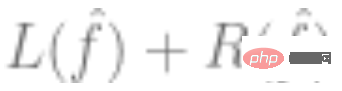der kleinste ist, den Verlust darstellt (der angibt, wie nahe der vorhergesagte Wert am wahren Wert liegt) und # 🎜🎜# ist ein optionaler Regularisierungsbegriff.

3. Je kleiner der Gesamtverlust des Modells ist, desto besser, das heißt, der Wert des Generalisierungsfehlers

ist relativ gering.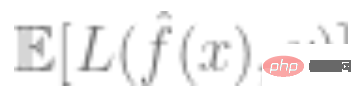

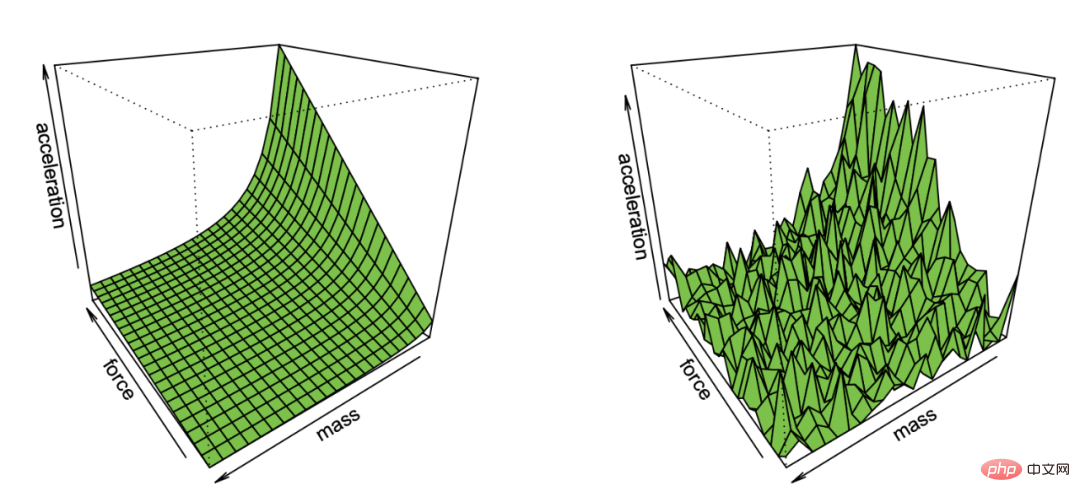
Effron zeigt die Wiederherstellung des ersten Newtonschen Gesetzes aus Beobachtungen, die Rauschen enthalten

Dieses sehr allgemeine Beispiel enthält tatsächlich viele Dinge wie Lineare Regression der kleinsten Quadrate, nächste Nachbarn, Training neuronaler Netze und mehr. In klassischen statistischen Szenarien stoßen wir normalerweise auf die folgende Situation:

Kompromiss: Nehmen Sie eine optimierte Sammlung von Modellen an (wenn die Funktion nicht konvex ist oder einen Regularisierungsterm enthält, wählen Sie den Algorithmus und die Regularisierung sorgfältig aus Die Abweichung des erhaltenen Modellsatzes ist die größte Annäherung an den wahren Wert, den das Element erreichen kann. Je größer der Satz, desto kleiner die Abweichung, und je größer, desto mehr Stichproben werden benötigt Um seine Zugehörigkeit einzuschränken, ist der Gesamtverallgemeinerungsfehler umso größer, je größer die Varianz des Ausgabemodells des Algorithmus ist Gesamtfehler. Tatsächlich begründen Geman et al. ihren Pessimismus gegenüber neuronalen Netzen damit, dass die grundlegenden Einschränkungen, die das Bias-Varianz-Dilemma mit sich bringt, für alle nichtparametrischen Inferenzmodelle gelten, einschließlich neuronaler Netze Dies gilt nicht immer: Beim statistischen Lernen verbessern mehr Merkmale oder Daten nicht unbedingt die Leistung. Ebenso ist es schwierig, aus Daten zu lernen, die viele irrelevante Merkmale enthalten. Wenn die Daten aus einer von zwei Verteilungen stammen (z. B. und), ist dies schwieriger, als jede Verteilung einzeln zu lernen hängt mit der Parametersumme zusammen, das heißt, die Anzahl der Datenpunkte ist ungefähr gleich. In diesem Fall sind etwa k Stichproben erforderlich, um zu starten. Sobald Sie dies jedoch tun, stehen Sie vor einer Situation sinkender Renditen, d Um eine Genauigkeit von 90 % zu erreichen, sind etwa 10 zusätzliche Punkte erforderlich, um die Genauigkeit auf 95 % zu erhöhen. Im Allgemeinen möchte man mit zunehmenden Ressourcen (ob Daten, Modellkomplexität oder Berechnung) immer mehr Feindifferenzierung erreichen Freischalten spezifischer neuer Funktionen

Starke Abhängigkeit von Daten: Bei der Anpassung eines Modells an hochdimensionale Daten kann jedes kleine Detail einen großen Unterschied machen, nicht jedoch Zu erwähnen ist die Verwendung verschiedener hochdimensionaler Optimierer, die relativ „einfach“ voneinander sind. Es wird normalerweise davon ausgegangen, dass die Daten unabhängig von einer bestimmten Verteilung abgetastet werden. Obwohl Punkte in der Nähe der Entscheidungsgrenze schwierig zu klassifizieren sind Aufgrund des Phänomens der Messkonzentration in hohen Dimensionen kann davon ausgegangen werden, dass die meisten Punkte nahe beieinander liegen. Daher ist der Abstandsunterschied zwischen Datenpunkten nicht groß. Allerdings können Mischungsmodelle diesen Unterschied zeigen Bei anderen oben genannten Problemen kommt dieser Unterschied häufig in der Statistik vor. 🎜🎜#Szenario B: Mathematik lernen

In diesem Szenario gehen wir davon aus, dass Sie den Schülern Mathematik (z. B. das Berechnen von Ableitungen) durch einige Anweisungen beibringen möchten und Übungen. Dieses Szenario hat keine formale Definition, aber es gibt einige qualitative Merkmale: In diesem Fall erlernen die Schüler eine Fertigkeit und nicht die Schätzung/Vorhersage einer bestimmten Menge. Auch wenn die Funktion, die Übungen den Lösungen zuordnet, nicht als „Black Box“ zum Lösen bestimmter unbekannter Aufgaben verwendet werden kann, können die mentalen Modelle, die Schüler beim Lösen dieser Probleme entwickeln, dennoch für unbekannte Aufgaben nützlich sein.

Je mehr, desto besser: Im Allgemeinen schneiden Studierende, die mehr Fragen beantworten und ein breiteres Spektrum an Fragetypen abdecken, besser ab. Das gleichzeitige Bearbeiten einiger Analysis- und Algebra-Fragen führt nicht zu einer Verschlechterung der Analysis-Ergebnisse der Schüler, kann aber dazu beitragen, ihre Analysis-Ergebnisse zu verbessern.

Von der Verbesserung der Fähigkeiten bis hin zur automatisierten Darstellung: Obwohl es in einigen Fällen auch abnehmende Erfolge bei der Problemlösung gibt, lernen die Schüler in mehreren Phasen. Es gibt eine Phase, in der das Lösen einiger Probleme hilft, die Konzepte zu verstehen und neue Fähigkeiten freizuschalten. Wenn Schüler eine bestimmte Art von Problem wiederholen, bilden sie außerdem einen automatisierten Problemlösungsprozess aus, wenn sie ähnliche Probleme sehen, und wandeln sich von der vorherigen Fähigkeitsverbesserung zur automatischen Problemlösung um.

Leistung unabhängig von Daten und Verlust: Es gibt mehr als eine Möglichkeit, mathematische Konzepte zu vermitteln. Schüler, die mit unterschiedlichen Büchern, Lehrmethoden oder Bewertungssystemen lernen, lernen am Ende möglicherweise die gleichen Inhalte und verfügen über ähnliche mathematische Fähigkeiten.

Manche Probleme sind schwieriger: Bei Mathematikübungen sehen wir oft starke Zusammenhänge zwischen der Art und Weise, wie verschiedene Schüler das gleiche Problem lösen. Es scheint, dass es für ein Problem einen inhärenten Schwierigkeitsgrad und einen natürlichen Schwierigkeitsgrad gibt, der sich am besten zum Lernen eignet.

Ist Deep Learning eher eine statistische Schätzung oder die Lernfähigkeit von Schülern?

Welche der beiden oben genannten Metaphern eignet sich besser zur Beschreibung von modernem Deep Learning? Was macht es konkret erfolgreich? Die Anpassung statistischer Modelle kann mithilfe von Mathematik und Code gut ausgedrückt werden. Tatsächlich trainiert die kanonische Pytorch-Trainingsschleife tiefe Netzwerke durch empirische Risikominimierung:

Auf einer tieferen Ebene ist die Beziehung zwischen diesen beiden Szenarien nicht klar. Um genauer zu sein, hier als Beispiel eine konkrete Lernaufgabe. Stellen Sie sich einen Klassifizierungsalgorithmus vor, der mit dem Ansatz „selbstüberwachtes Lernen + lineare Erkennung“ trainiert wurde. Das spezifische Algorithmustraining ist wie folgt:

​1. Angenommen, die Daten sind eine Sequenz, wobei ein bestimmter Datenpunkt (z. B. ein Bild) und die Bezeichnung ist. ​

​2. Holen Sie sich zuerst das tiefe neuronale Netzwerk, das die Funktion darstellt 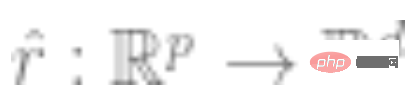. Eine selbstüberwachte Verlustfunktion irgendeiner Art wird trainiert, indem sie minimiert wird, indem nur Datenpunkte und keine Beschriftungen verwendet werden. Beispiele für solche Verlustfunktionen sind Rekonstruktion (Wiederherstellung der Eingabe mit anderen Eingaben) oder kontrastives Lernen (die Kernidee besteht darin, positive und negative Stichproben im Merkmalsraum zu vergleichen, um die Merkmalsdarstellung der Stichprobe zu lernen).

3. Passen Sie einen linearen Klassifikator 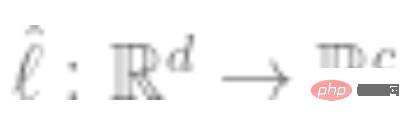(das ist die Anzahl der Klassen) unter Verwendung der vollständig gekennzeichneten Daten an, um den Kreuzentropieverlust zu minimieren. Unser endgültiger Klassifikator lautet:

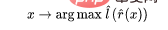
Schritt 3 funktioniert nur für lineare Klassifikatoren, daher geschieht die „Magie“ in Schritt 2 (selbstüberwachtes Lernen tiefer Netzwerke). Beim selbstüberwachten Lernen gibt es einige wichtige Eigenschaften:

Erlernen Sie eine Fähigkeit, anstatt sich einer Funktion anzunähern: Beim selbstüberwachten Lernen geht es nicht darum, eine Funktion zu approximieren, sondern darum, Darstellungen zu lernen, die für eine Vielzahl nachgelagerter Aufgaben verwendet werden können (dies ist das vorherrschende Paradigma in der Verarbeitung natürlicher Sprache). Die Erlangung nachgelagerter Aufgaben durch lineare Sondierung, Feinabstimmung oder Anregung ist zweitrangig.

Je mehr, desto besser: Beim selbstüberwachten Lernen verbessert sich die Qualität der Darstellung mit zunehmender Datenmenge und verschlechtert sich nicht durch die Vermischung von Daten aus mehreren Quellen. Tatsächlich gilt: Je vielfältiger die Daten, desto besser.

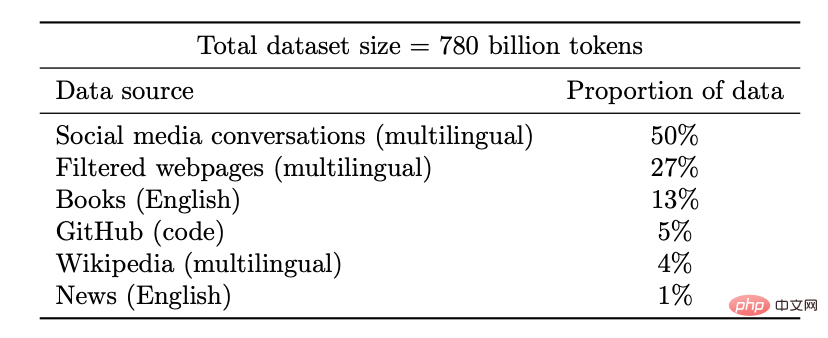
Coogle PaLM-Modell-Datensatz

Erschließen Sie neue Funktionen: Mit steigenden Ressourceninvestitionen (Daten, Rechenleistung, Modellgröße) werden auch Deep-Learning-Modelle diskontinuierlich verbessert. Dies wurde auch in einigen Kombinationsumgebungen nachgewiesen.

Mit zunehmender Modellgröße zeigt PaLM diskrete Verbesserungen bei Benchmarks und schaltet überraschende Funktionen frei, wie zum Beispiel die Erklärung, warum ein Witz lustig ist.

Die Leistung ist nahezu unabhängig von Verlusten oder Daten: Es gibt mehrere selbstüberwachte Verluste, mehrere Kontrast- und Rekonstruktionsverluste werden tatsächlich in der Bildforschung verwendet, Sprachmodelle verwenden eine einseitige Rekonstruktion (Vorhersage des nächsten Tokens) oder verwenden ein Maskenmodell, um Vorhersagen zu treffen von links und rechts Die Maskeneingabe des Tokens. Es ist auch möglich, leicht unterschiedliche Datensätze zu verwenden. Diese können sich auf die Effizienz auswirken, aber solange „vernünftige“ Entscheidungen getroffen werden, verbessert die ursprüngliche Ressource die Vorhersageleistung oft stärker als der spezifische Verlust oder der verwendete Datensatz.

Einige Fälle sind schwieriger als andere: Dieser Punkt bezieht sich nicht speziell auf selbstüberwachtes Lernen. Datenpunkte scheinen einen inhärenten „Schwierigkeitsgrad“ zu haben. Tatsächlich haben unterschiedliche Lernalgorithmen unterschiedliche „Fähigkeitsniveaus“ und unterschiedliche Datenanalysen unterschiedliche „Schwierigkeitsniveaus“ (die Wahrscheinlichkeit, dass ein Klassifikator einen Punkt korrekt klassifiziert, steigt monoton mit der Fähigkeit und nimmt monoton mit der Schwierigkeit ab).

Das Paradigma „Fähigkeit vs. Schwierigkeit“ ist die klarste Erklärung für das von Recht et al. und Miller et al. entdeckte Phänomen „Genauigkeit auf dem Spiel“. Das Papier von Kaplen, Ghosh, Garg und Nakkiran zeigt auch, wie unterschiedliche Eingaben in einem Datensatz inhärente „Schwierigkeitsprofile“ haben, die im Allgemeinen für verschiedene Modellfamilien robust sind.

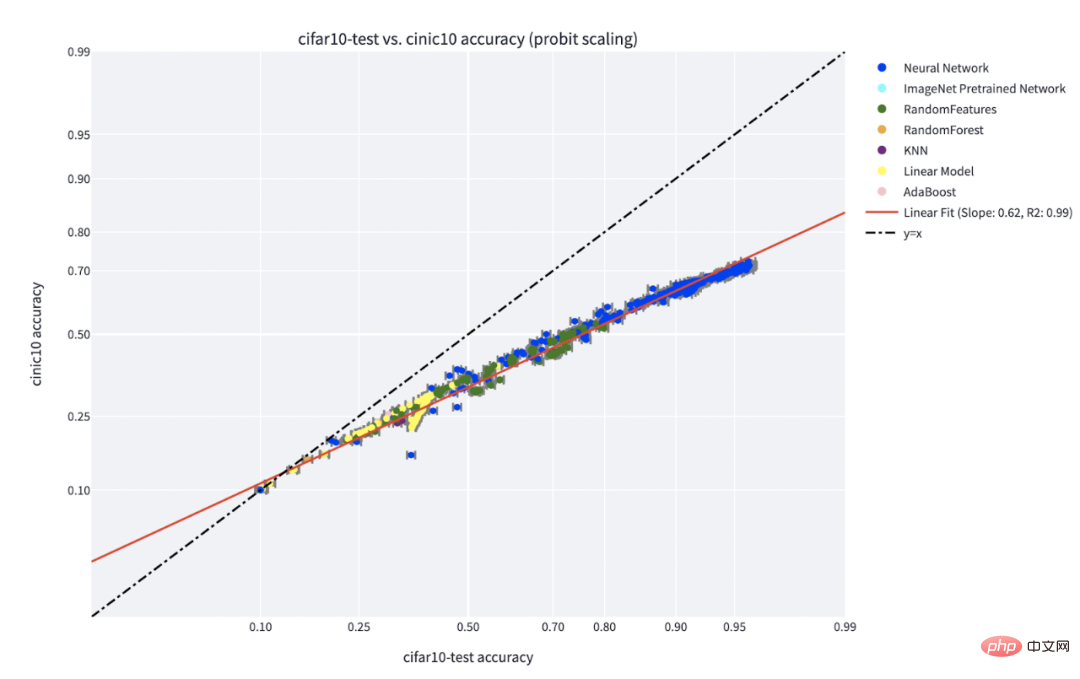
C**-Genauigkeit beim Linienphänomen für einen auf IFAR-10 trainierten und auf CINIC-10 getesteten Klassifikator. Quelle der Abbildung: https://millerjohnp-linearfits-app-app-ryiwcq.streamlitapp.com/

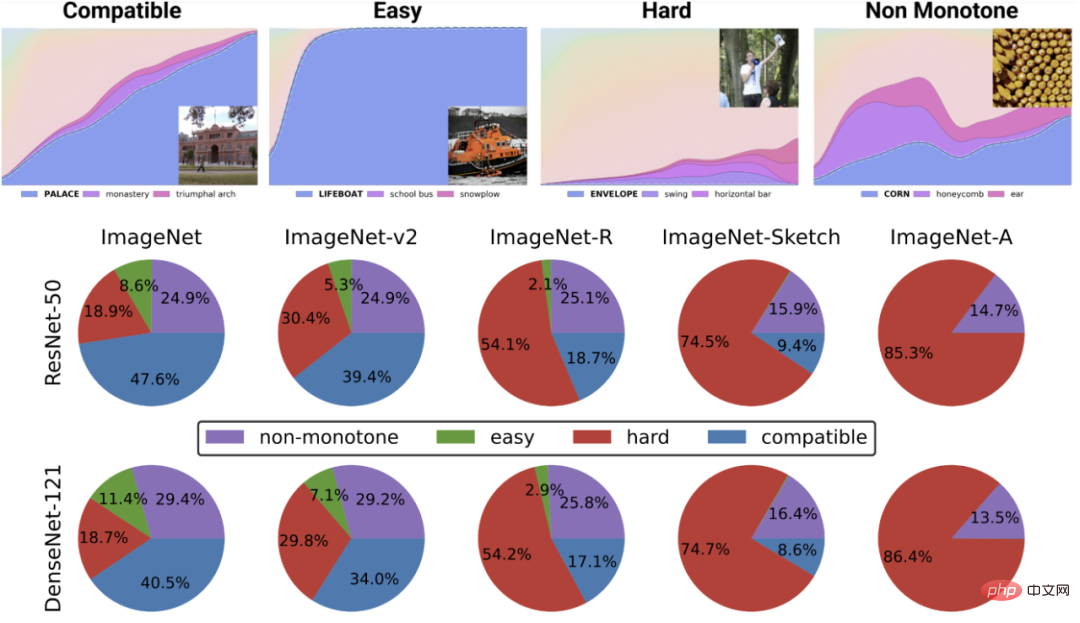
Die obere Abbildung zeigt verschiedene Softmax-Wahrscheinlichkeiten für die wahrscheinlichste Klasse als Funktion der globalen Genauigkeit eines bestimmten Klassenklassifikators , die Kategorie wird nach Trainingszeit indiziert. Das untere Kreisdiagramm zeigt die Zerlegung verschiedener Datensätze in verschiedene Punkttypen (beachten Sie, dass diese Zerlegung für verschiedene neuronale Strukturen ähnlich ist).

Training ist Lehren: Beim Training moderner großer Modelle geht es eher darum, Schüler zu unterrichten, als das Modell an die Daten anzupassen. Wenn Schüler etwas nicht verstehen oder sich müde fühlen, „ruhen“ sie sich aus oder probieren verschiedene Methoden aus (Trainingsunterschiede). Metas große Modelltrainingsprotokolle sind aufschlussreich – zusätzlich zu Hardwareproblemen können wir auch Eingriffe wie das Wechseln verschiedener Optimierungsalgorithmen während des Trainings und sogar das Erwägen eines „Hot-Swapping“ von Aktivierungsfunktionen (GELU zu RELU) erkennen. Letzteres macht wenig Sinn, wenn Sie sich das Modelltraining eher als Anpassen der Daten und nicht als Erlernen einer Darstellung vorstellen.

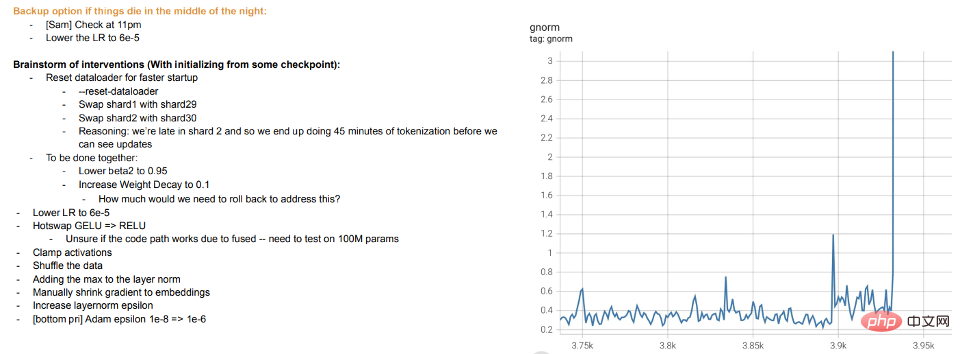
Meta-Trainingsprotokoll-Auszug

4.1 Aber wie sieht es mit überwachtem Lernen aus?

Selbstüberwachtes Lernen wurde bereits besprochen, aber das typische Beispiel für Deep Learning ist immer noch überwachtes Lernen. Schließlich kam der „ImageNet-Moment“ des Deep Learning von ImageNet. Gilt also das, was oben besprochen wurde, immer noch für diese Einstellung?

Erstens war die Entstehung des überwachten, groß angelegten Deep Learning dank der Verfügbarkeit großer, qualitativ hochwertiger, gekennzeichneter Datensätze (z. B. ImageNet) eher zufällig. Wenn Sie eine gute Vorstellungskraft haben, können Sie sich eine alternative Geschichte vorstellen, in der Deep Learning zunächst durch unbeaufsichtigtes Lernen Durchbrüche in der Verarbeitung natürlicher Sprache erzielte, bevor es zu Vision und überwachtem Lernen überging.

Zweitens gibt es Hinweise darauf, dass sich überwachtes Lernen und selbstüberwachtes Lernen tatsächlich „intern“ ähnlich verhalten, obwohl völlig unterschiedliche Verlustfunktionen verwendet werden. Beide erzielen in der Regel die gleiche Leistung. Insbesondere kann man für jeden die ersten k Schichten eines Modells der Tiefe d, das mit Selbstüberwachung trainiert wurde, mit den letzten d-k Schichten des überwachten Modells mit geringem Leistungsverlust kombinieren.

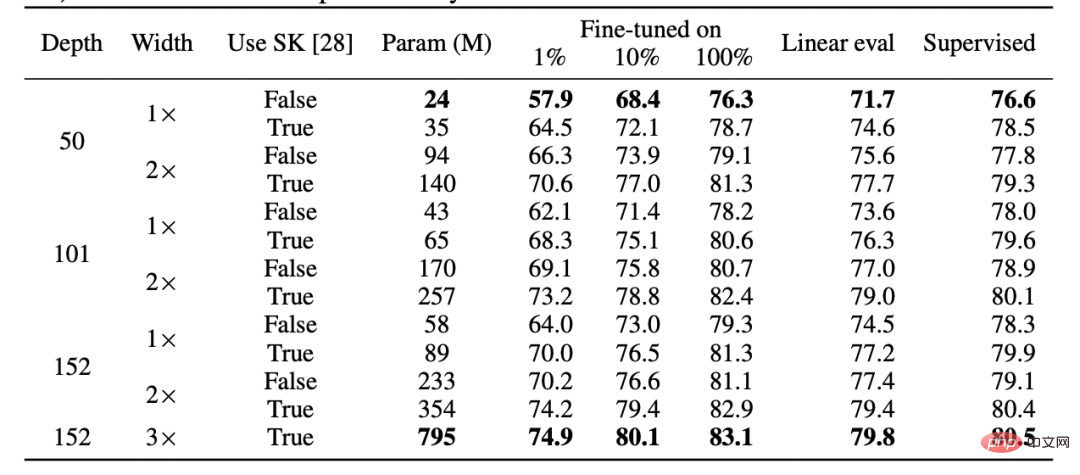
Tabelle für SimCLR v2-Papier. Bitte beachten Sie die allgemeine Leistungsähnlichkeit zwischen überwachtem Lernen, fein abgestimmter (100 %) selbstüberwachter und selbstüberwachter + linearer Erkennung (Quelle: https://arxiv.org/abs/2006.10029)

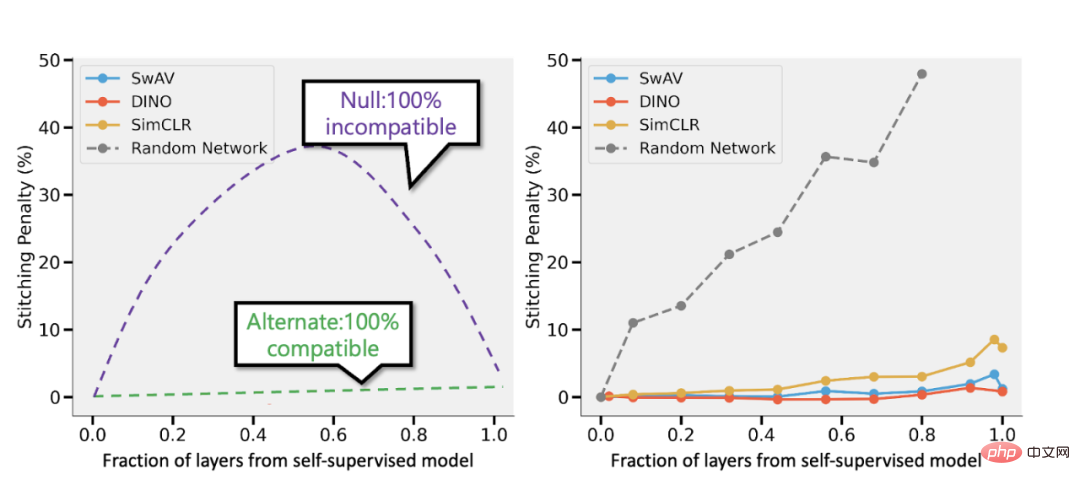
Spliced ​​​​aus dem überwachten Modell und dem überwachten Modell von Bansal et al. (https://arxiv.org/abs/2106.07682). Links: Wenn die Genauigkeit des selbstüberwachten Modells (sagen wir) 3 % niedriger ist als die des überwachten Modells, führt eine vollständig kompatible Darstellung zu einer Spleißeinbuße von p 3 %, wenn p Teile der Schicht vom selbstüberwachten Modell stammen Modell. Wenn die Modelle völlig inkompatibel sind, ist zu erwarten, dass die Genauigkeit dramatisch abnimmt, wenn mehr Modelle zusammengeführt werden. Rechts: Tatsächliche Ergebnisse, die verschiedene selbstüberwachte Modelle kombinieren.

Der Vorteil selbstüberwachter + einfacher Modelle besteht darin, dass sie Feature-Learning oder „Deep-Learning-Magie“ (durchgeführt durch eine Tiefendarstellungsfunktion) mit statistischer Modellanpassung (durchgeführt durch einen linearen oder anderen „einfachen“ Klassifikator darüber) kombinieren können diese Darstellung) Trennung.

Auch wenn es sich hier eher um eine Spekulation handelt, ist es doch eine Tatsache, dass „Meta-Lernen“ oft mit Lerndarstellungen gleichgesetzt zu werden scheint (siehe: https://arxiv.org/abs/1909.09157, https://arxiv. org/abs /2206.03271), was als ein weiterer Beweis dafür gewertet werden kann, dass dies weitgehend unabhängig von den Zielen der Modelloptimierung geschieht.

4.2 Was tun bei Überparametrierung?

In diesem Artikel werden einige Beispiele übersprungen, die als klassische Beispiele für Unterschiede zwischen statistischen Lernmodellen und Deep Learning in der Praxis gelten: das Fehlen eines „Bias-Varianz-Kompromisses“ und die Fähigkeit überparametrisierter Modelle, gut zu verallgemeinern.

Warum überspringen? Dafür gibt es zwei Gründe:

• Wenn überwachtes Lernen tatsächlich dem selbstüberwachten + einfachen Lernen gleichkommt, kann dies zunächst seine Generalisierungsfähigkeit erklären.
• Zweitens ist eine Überparametrisierung nicht der Schlüssel zum Erfolg von Deep Learning. Das Besondere an tiefen Netzwerken ist nicht, dass sie im Vergleich zur Anzahl der Stichproben groß sind, sondern dass sie in absoluten Zahlen groß sind. Tatsächlich ist das Modell beim unbeaufsichtigten/selbstüberwachten Lernen normalerweise nicht überparametrisiert. Selbst für sehr große Sprachmodelle sind ihre Datensätze größer.

Das „Deep Bootstrap“-Papier von Nakkiran-Neyshabur-Sadghi zeigt, dass sich moderne Architekturen im „überparametrisierten“ oder „unterabgetasteten“ Regime ähnlich verhalten (das Modell wird bis dahin über viele Epochen hinweg auf begrenzten Daten trainiert). Überanpassungen: „Reale Welt“ in der obigen Abbildung), dasselbe gilt im „unterparametrisierten“ oder „Online“-Zustand (das Modell wird für eine einzelne Epoche trainiert und jede Stichprobe wird nur einmal angezeigt: „Ideale Welt“ in der obigen Abbildung). Bildquelle: https://arxiv.org/abs/2010.08127

Zusammenfassung

Statistisches Lernen spielt beim Deep Learning sicherlich eine Rolle. Doch trotz der Verwendung ähnlicher Terminologie und Codes wird bei der Betrachtung von Deep Learning als einfachem Anpassen eines Modells mit mehr Parametern als bei einem klassischen Modell vieles außer Acht gelassen, was für den Erfolg entscheidend ist. Auch die Metapher, Schülern Mathematik beizubringen, ist nicht perfekt.

Obwohl Deep Learning wie die biologische Evolution viele wiederverwendete Regeln enthält (z. B. Gradientenabstieg mit Erfahrungsverlust), kann es zu hochkomplexen Ergebnissen führen. Es scheint, dass verschiedene Komponenten des Netzwerks zu unterschiedlichen Zeiten unterschiedliche Dinge lernen, einschließlich Repräsentationslernen, prädiktive Anpassung, implizite Regularisierung und reines Rauschen. Forscher sind immer noch auf der Suche nach der richtigen Linse, um Fragen zum Thema Deep Learning zu stellen, geschweige denn zu beantworten.

Das obige ist der detaillierte Inhalt vonLernen = passend? Sind Deep Learning und klassische Statistik dasselbe?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!