 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte
 KI
KI
 KI löst Hochschulmathematikprobleme in wenigen Sekunden, erreicht eine Genauigkeitsrate von über 80 % und fungiert auch als Fragenlehrer
KI löst Hochschulmathematikprobleme in wenigen Sekunden, erreicht eine Genauigkeitsrate von über 80 % und fungiert auch als Fragenlehrer
KI löst Hochschulmathematikprobleme in wenigen Sekunden, erreicht eine Genauigkeitsrate von über 80 % und fungiert auch als Fragenlehrer

Vielleicht wurden die Mathe-Testfragen, die Sie beantwortet haben, maschinell generiert.
MIT-Studenten können mathematische Themen wie multivariate Analysis, Differentialgleichungen und lineare Algebra mühelos lösen, aber diese überfordern das Modell des maschinellen Lernens. Weil Modelle des maschinellen Lernens nur mathematische Fragen auf Grund- oder Oberstufenniveau beantworten können und nicht immer die richtige Antwort finden.
Jetzt verwenden Forscher des MIT, der Columbia University, der Harvard University und der University of Waterloo das Lernen mit kleinen Stichproben und den Codex von OpenAI, um Programme automatisch zu synthetisieren und universitäre Mathematikprobleme in wenigen Sekunden zu lösen und so das Niveau des Menschen zu erreichen. Die Forschung wurde in den Proceedings of the National Academy of Sciences (PNAS) veröffentlicht.
Darüber hinaus kann das Modell die generierten Lösungen erklären und schnell neue College-Mathematikprobleme generieren. Als die Forscher den Schülern diese maschinell generierten Fragen zeigten, konnten die Schüler nicht einmal erkennen, ob die Fragen von einem Algorithmus oder von einem Menschen generiert wurden.
Diese Forschung kann auch zur Optimierung der Erstellung von Kursinhalten genutzt werden, was besonders für Schulen mit Tausenden von Schülern und massiven offenen Online-Kursen (MOOCs) nützlich ist. Das System kann auch als Online-Tutor fungieren und den Schülern die Schritte zur Lösung mathematischer Probleme zeigen.

Papieradresse: https://www.pnas.org/doi/epdf/10.1073/pnas.2123433119
Die Forschungsmethode vereint drei Innovationen:
- Anders als Diese Forschung führt nur eine Feinabstimmung des Codes durch, während sie mit kleinen Beispiellernprogrammen arbeitet, um mathematische Probleme richtig zu lösen , Lösungen erläutern und neue Fragen generieren.
- Beispiele für neue Fragen, die durch diese Forschung generiert wurden, sind wie folgt.
Ein Modell, das Fragen beantworten, lösen und stellen kann
Das Forschungsteam hat fast zwei Jahre an diesem Projekt gearbeitet. Sie fanden heraus, dass ein Modell, das nur mit Text vorab trainiert wurde, bei Mathematikproblemen der Oberstufe nicht mehr als 8 % Genauigkeit erreichen konnte, während ein graphisches neuronales Netzwerkmodell bei Kursproblemen für maschinelles Lernen gut abschneiden konnte, aber es würde eine Woche dauern, zu trainieren. 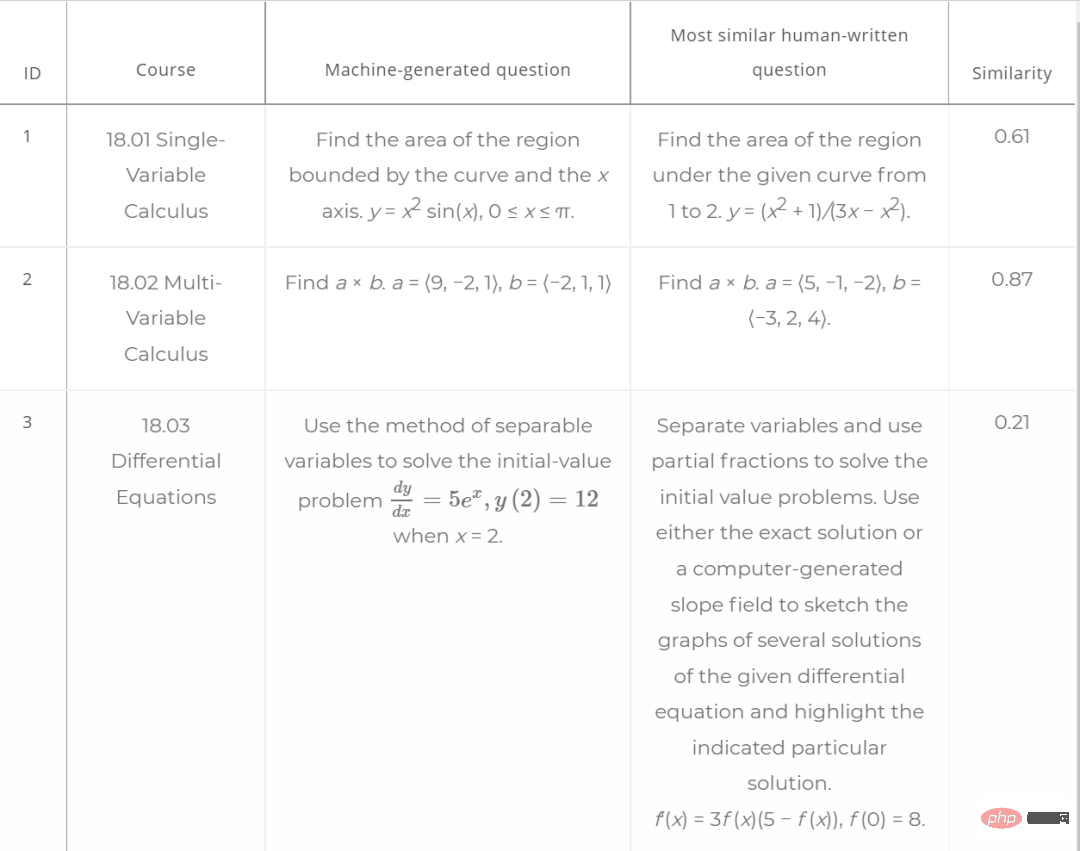
Für den MATH-Datensatz wurden im Rahmen der Studie zufällig 15 Fragen aus sechs Themen im Datensatz ausgewählt (Algebra, Zählen und Wahrscheinlichkeit, Fortgeschrittene Algebra, Zahlentheorie, Vorläufige Algebra und Analysis).
Bevor die Forscher diese Programmieraufgaben in das neuronale Netzwerk einspeisten, fügten sie einen neuen Schritt hinzu, der es ihnen ermöglichte, frühere Versuche deutlich zu übertreffen.
 unterscheidet sich von Netzwerken wie GPT-3, die nur auf Text vortrainiert sind. Sie wandelten diese Probleme in Programmieraufgaben um und wendeten Programmsynthese und Few-Shot-Lerntechniken an. Ein mathematisches Problem in eine Programmieraufgabe umzuwandeln, kann so einfach sein wie das Umschreiben des Problems, den Abstand zwischen zwei Punkten zu ermitteln, wie das Schreiben eines Programms, um den Unterschied zwischen zwei Punkten zu ermitteln.
unterscheidet sich von Netzwerken wie GPT-3, die nur auf Text vortrainiert sind. Sie wandelten diese Probleme in Programmieraufgaben um und wendeten Programmsynthese und Few-Shot-Lerntechniken an. Ein mathematisches Problem in eine Programmieraufgabe umzuwandeln, kann so einfach sein wie das Umschreiben des Problems, den Abstand zwischen zwei Punkten zu ermitteln, wie das Schreiben eines Programms, um den Unterschied zwischen zwei Punkten zu ermitteln.
Es ist erwähnenswert, dass diese Forschung nicht nur Codex für Text vortrainiert, sondern auch den Code so verfeinert hat, dass er Programme zur Lösung umfangreicher mathematischer Probleme generieren kann.
Vorab trainierte Modelle, die Millionen von Codebeispielen aus Online-Repositories zeigen. Da die Trainingsdaten des Modells Millionen natürlichsprachlicher Wörter und Millionen Codezeilen umfassen, kann es Beziehungen zwischen Textausschnitten und Codeausschnitten lernen.
Wie in der folgenden Abbildung dargestellt, verwendet diese Studie Zero-Shot- und Small-Shot-Lernen, um automatisch ein Programm zu generieren, das 81 % der mathematischen Probleme lösen kann. Anschließend verwenden sie den Codex, um das resultierende Programm zu interpretieren. Das generierte Programm kann Antworten in vielen Formen ausgeben. Beispielsweise liefert die Berechnung und Darstellung der geometrischen Form der Singularwertzerlegung (SVD) nicht nur die richtige Antwort, sondern auch die entsprechende Erklärung! 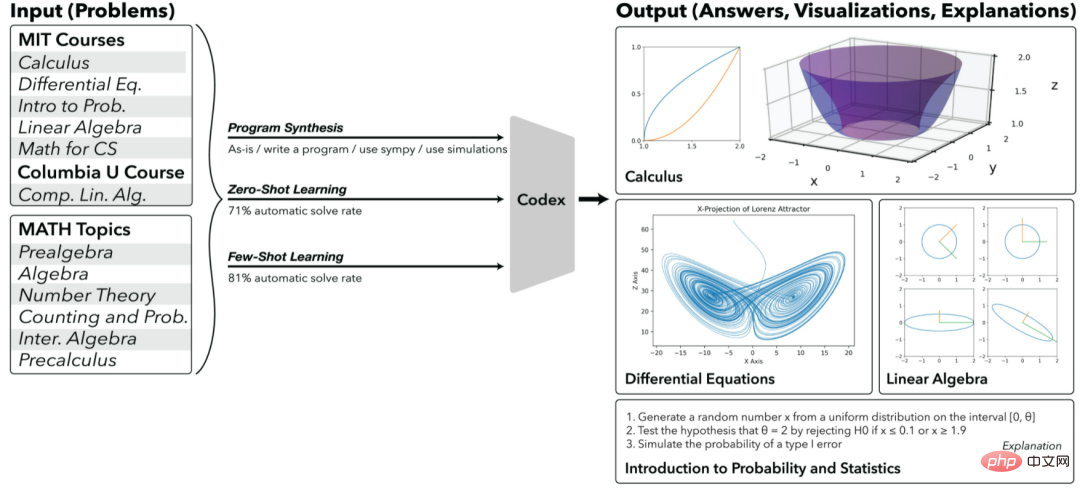 Wenden Sie neuronale Netze OpenAI Codex an, um mathematische Probleme zu lösen, zu interpretieren und zu generieren.
Wenden Sie neuronale Netze OpenAI Codex an, um mathematische Probleme zu lösen, zu interpretieren und zu generieren.
Drori, einer der Autoren des Artikels, erklärte, dass viele mathematische Probleme mithilfe von Diagrammen oder Bäumen gelöst werden können, es jedoch schwierig sei, in Textform geschriebene Probleme in diese Darstellung umzuwandeln. Da das Modell jedoch die Beziehung zwischen Text und Code gelernt hat, kann es Textfragen in Code umwandeln, indem es einfach ein paar Beispiele für Fragecode angibt und dann den Code ausführt, um die Frage zu beantworten.
„Wenn Sie Fragen nur mit Text stellen, ist es für maschinelle Lernmodelle schwierig, Antworten zu geben, selbst wenn die Antwort im Text enthalten sein könnte, und diese Arbeit füllt die fehlenden Teile des Codes und der Programmsynthese auf“, sagte Drori .
Drori fügte außerdem hinzu, dass diese Arbeit die erste ist, die ein Mathematikproblem für Studenten löst und die Genauigkeit von 8 % auf über 80 % verbessert.
Kontext hinzufügen
Es ist nicht immer einfach, ein mathematisches Problem in eine Programmieraufgabe umzuwandeln. Bei einigen Problemen müssen Forscher Kontext hinzufügen, damit neuronale Netze das Problem richtig lösen können. Ein Student erlernt dieses Hintergrundwissen während des Kurses, neuronale Netze verfügen jedoch nicht über dieses Hintergrundwissen, es sei denn, der Forscher gibt dies ausdrücklich an.
Zum Beispiel müssen sie erklären, dass sich das Netzwerk im Text auf ein neuronales Netzwerk und nicht auf ein Kommunikationsnetzwerk bezieht. Oder sie müssen dem Modell möglicherweise mitteilen, welches Programmierpaket verwendet werden soll. Möglicherweise müssen sie auch bestimmte Definitionen angeben, beispielsweise müssen sie dem Modell bei einer Frage zu Spielkarten mitteilen, dass jedes Deck 52 Karten enthält.
Die Studie speist diese Programmieraufgaben zusammen mit dem enthaltenen Kontext und Beispielen automatisch in ein vorab trainiertes und fein abgestimmtes neuronales Netzwerk ein, das ein Programm ausgibt, das normalerweise die richtige Antwort liefert. Mehr als 80 % der Fragen waren richtig.
Die Forscher nutzten ihr Modell auch zur Generierung von Fragen, indem sie einem neuronalen Netzwerk eine Reihe mathematischer Fragen zu einem Thema gaben und es dann eine neue Frage erstellen ließen. Beispielsweise gibt es das Problem der Quantenerkennung horizontaler und vertikaler Linien, das ein neues Problem der Quantenerkennung von Diagonalen schafft. Es geht also nicht nur darum, neue Probleme zu schaffen, indem Werte und Variablen in bestehenden Problemen ersetzt werden.
Von Menschen gestellte Fragen vs. maschinengenerierte Fragen
Die Forscher testeten diese Fragen, indem sie College-Studenten die maschinengenerierten Fragen zeigten. Die Forscher gaben den Studierenden nach dem Zufallsprinzip zehn Aufgaben aus einem Mathematik-Grundkurs; fünf wurden von Menschen erstellt und fünf von Maschinen generiert.
Die Studierenden konnten nicht erkennen, ob die maschinell generierten Fragen von einem Algorithmus oder von einem Menschen generiert wurden, und sie gaben ähnliche Bewertungen zur Schwierigkeit und Angemessenheit des Kurses ab.
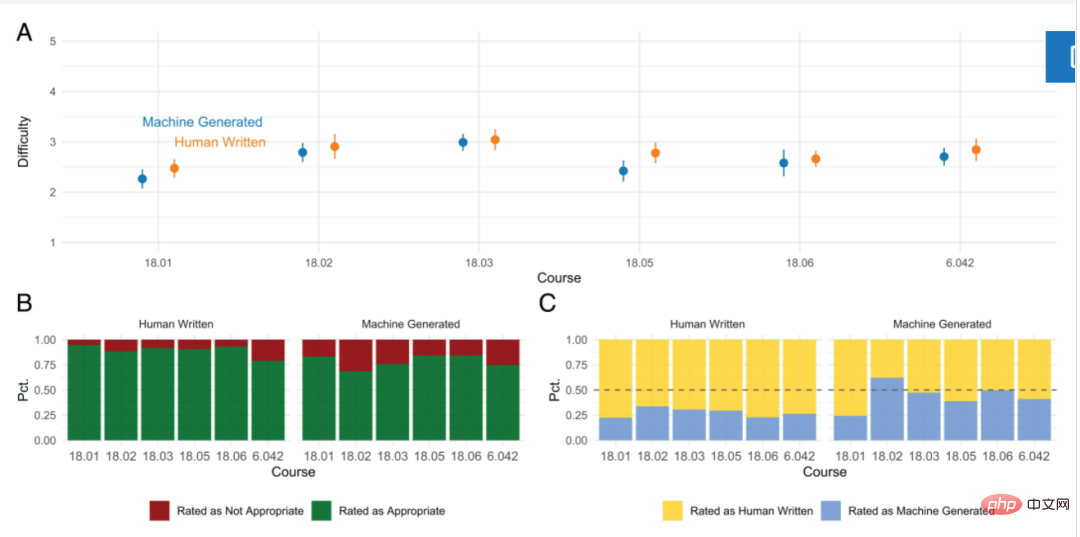
Drori stellte jedoch fest, dass diese Arbeit nicht dazu gedacht ist, menschliche Professoren zu ersetzen.
"Die Genauigkeitsrate hat jetzt 80 % erreicht, aber sie wird nicht 100 % erreichen. Jedes Mal, wenn Sie ein Problem lösen, wird jemand ein schwierigeres Problem stellen. Aber diese Arbeit bietet Menschen eine Möglichkeit, mit dem Einsatz von maschinellem Lernen zu beginnen „Wir gehen davon aus, dass dies große Auswirkungen auf die Hochschulbildung haben wird“, sagte Drori.
Das Forschungsteam freut sich über den Erfolg ihrer Methode und hat ihre Arbeit auf die Bearbeitung mathematischer Beweise ausgeweitet. Sie planen auch, einige Einschränkungen zu beheben. Derzeit kann das Modell keine Fragen mithilfe einer visuellen Komponente beantworten oder Probleme lösen zu rechnerischen Einschränkungen. Komplexe und schwer zu berechnende Probleme.
Neben der Überwindung dieser Hindernisse zielt die Forschung auch darauf ab, das Modell auf Hunderte von Kursen zu skalieren. Mit diesen Kursen werden mehr Daten generiert, um die Automatisierung zu erhöhen und Einblicke in die Kursgestaltung und den Lehrplan zu geben.
Das obige ist der detaillierte Inhalt vonKI löst Hochschulmathematikprobleme in wenigen Sekunden, erreicht eine Genauigkeitsrate von über 80 % und fungiert auch als Fragenlehrer. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1380
1380
 52
52
 Debian Mail Server Firewall -Konfigurationstipps
Apr 13, 2025 am 11:42 AM
Debian Mail Server Firewall -Konfigurationstipps
Apr 13, 2025 am 11:42 AM
Das Konfigurieren der Firewall eines Debian -Mailservers ist ein wichtiger Schritt zur Gewährleistung der Serversicherheit. Im Folgenden sind mehrere häufig verwendete Firewall -Konfigurationsmethoden, einschließlich der Verwendung von Iptables und Firewalld. Verwenden Sie Iptables, um Firewall so zu konfigurieren, dass Iptables (falls bereits installiert) installiert werden:
 Wie Debian Readdir sich in andere Tools integriert
Apr 13, 2025 am 09:42 AM
Wie Debian Readdir sich in andere Tools integriert
Apr 13, 2025 am 09:42 AM
Die Readdir -Funktion im Debian -System ist ein Systemaufruf, der zum Lesen des Verzeichnisgehalts verwendet wird und häufig in der C -Programmierung verwendet wird. In diesem Artikel wird erläutert, wie Readdir in andere Tools integriert wird, um seine Funktionalität zu verbessern. Methode 1: Kombinieren Sie C -Sprachprogramm und Pipeline zuerst ein C -Programm, um die Funktion der Readdir aufzurufen und das Ergebnis auszugeben:#include#include#includeIntmain (intargc, char*argv []) {Dir*Dir; structDirent*Eintrag; if (argc! = 2) {{
 So implementieren Sie die Dateisortierung nach Debian Readdir
Apr 13, 2025 am 09:06 AM
So implementieren Sie die Dateisortierung nach Debian Readdir
Apr 13, 2025 am 09:06 AM
In Debian -Systemen wird die Readdir -Funktion zum Lesen des Verzeichnisinhalts verwendet, aber die Reihenfolge, in der sie zurückgibt, ist nicht vordefiniert. Um Dateien in einem Verzeichnis zu sortieren, müssen Sie zuerst alle Dateien lesen und dann mit der QSORT -Funktion sortieren. Der folgende Code zeigt, wie Verzeichnisdateien mithilfe von Readdir und QSORT in Debian System sortiert werden:#include#include#include#include // benutzerdefinierte Vergleichsfunktion, verwendet für QSortIntCompare (constvoid*a, constvoid*b) {rettrcmp (*(*(*(
 Debian Mail Server SSL -Zertifikat -Installationsmethode
Apr 13, 2025 am 11:39 AM
Debian Mail Server SSL -Zertifikat -Installationsmethode
Apr 13, 2025 am 11:39 AM
Die Schritte zur Installation eines SSL -Zertifikats auf dem Debian Mail -Server sind wie folgt: 1. Installieren Sie zuerst das OpenSSL -Toolkit und stellen Sie sicher, dass das OpenSSL -Toolkit bereits in Ihrem System installiert ist. Wenn nicht installiert, können Sie den folgenden Befehl installieren: sudoapt-getupdatesudoapt-getinstallopenssl2. Generieren Sie den privaten Schlüssel und die Zertifikatanforderung als nächst
 So führen Sie die digitale Signaturüberprüfung mit Debian OpenSSL durch
Apr 13, 2025 am 11:09 AM
So führen Sie die digitale Signaturüberprüfung mit Debian OpenSSL durch
Apr 13, 2025 am 11:09 AM
Unter Verwendung von OpenSSL für die digitale Signaturüberprüfung im Debian -System können Sie folgende Schritte befolgen: Vorbereitung für die Installation von OpenSSL: Stellen Sie sicher, dass Ihr Debian -System OpenSSL installiert hat. Wenn nicht installiert, können Sie den folgenden Befehl verwenden, um es zu installieren: sudoaptupdatesudoaptininTallopenSSL, um den öffentlichen Schlüssel zu erhalten: Die digitale Signaturüberprüfung erfordert den öffentlichen Schlüssel des Unterzeichners. In der Regel wird der öffentliche Schlüssel in Form einer Datei wie Public_key.pe bereitgestellt
 Wie Debian OpenSSL verhindert, dass Mann-in-the-Middle-Angriffe
Apr 13, 2025 am 10:30 AM
Wie Debian OpenSSL verhindert, dass Mann-in-the-Middle-Angriffe
Apr 13, 2025 am 10:30 AM
In Debian Systems ist OpenSSL eine wichtige Bibliothek für Verschlüsselung, Entschlüsselung und Zertifikatverwaltung. Um einen Mann-in-the-Middle-Angriff (MITM) zu verhindern, können folgende Maßnahmen ergriffen werden: Verwenden Sie HTTPS: Stellen Sie sicher, dass alle Netzwerkanforderungen das HTTPS-Protokoll anstelle von HTTP verwenden. HTTPS verwendet TLS (Transport Layer Security Protocol), um Kommunikationsdaten zu verschlüsseln, um sicherzustellen, dass die Daten während der Übertragung nicht gestohlen oder manipuliert werden. Überprüfen Sie das Serverzertifikat: Überprüfen Sie das Serverzertifikat im Client manuell, um sicherzustellen, dass es vertrauenswürdig ist. Der Server kann manuell durch die Delegate -Methode der URLSession überprüft werden
 Wie man Debian Hadoop Log Management macht
Apr 13, 2025 am 10:45 AM
Wie man Debian Hadoop Log Management macht
Apr 13, 2025 am 10:45 AM
Wenn Sie Hadoop-Protokolle auf Debian verwalten, können Sie die folgenden Schritte und Best Practices befolgen: Protokollaggregation Aktivieren Sie die Protokollaggregation: Set Garn.log-Aggregation-Enable in true in der Datei marn-site.xml, um die Protokollaggregation zu aktivieren. Konfigurieren von Protokoll-Retentionsrichtlinien: Setzen Sie Garn.log-Aggregation.Retain-Sekunden, um die Retentionszeit des Protokolls zu definieren, z. B. 172800 Sekunden (2 Tage). Log Speicherpfad angeben: über Garn.n
 CentOS Shutdown -Befehlszeile
Apr 14, 2025 pm 09:12 PM
CentOS Shutdown -Befehlszeile
Apr 14, 2025 pm 09:12 PM
Der Befehl centOS stilldown wird heruntergefahren und die Syntax wird von [Optionen] ausgeführt [Informationen]. Zu den Optionen gehören: -h das System sofort stoppen; -P schalten Sie die Leistung nach dem Herunterfahren aus; -r neu starten; -t Wartezeit. Zeiten können als unmittelbar (jetzt), Minuten (Minuten) oder als bestimmte Zeit (HH: MM) angegeben werden. Hinzugefügten Informationen können in Systemmeldungen angezeigt werden.



