
Die Implementierungsdatenstruktur des int-Typs in cpython lautet wie folgt:
typedef struct _longobject PyLongObject;
struct _longobject {
PyObject_VAR_HEAD
digit ob_digit[1];
};
#define PyObject_VAR_HEAD PyVarObject ob_base;
typedef struct {
PyObject ob_base;
Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;
typedef struct _object {
_PyObject_HEAD_EXTRA
Py_ssize_t ob_refcnt;
struct _typeobject *ob_type;
} PyObject;Die obige Datenstruktur wird grafisch wie unten dargestellt dargestellt:
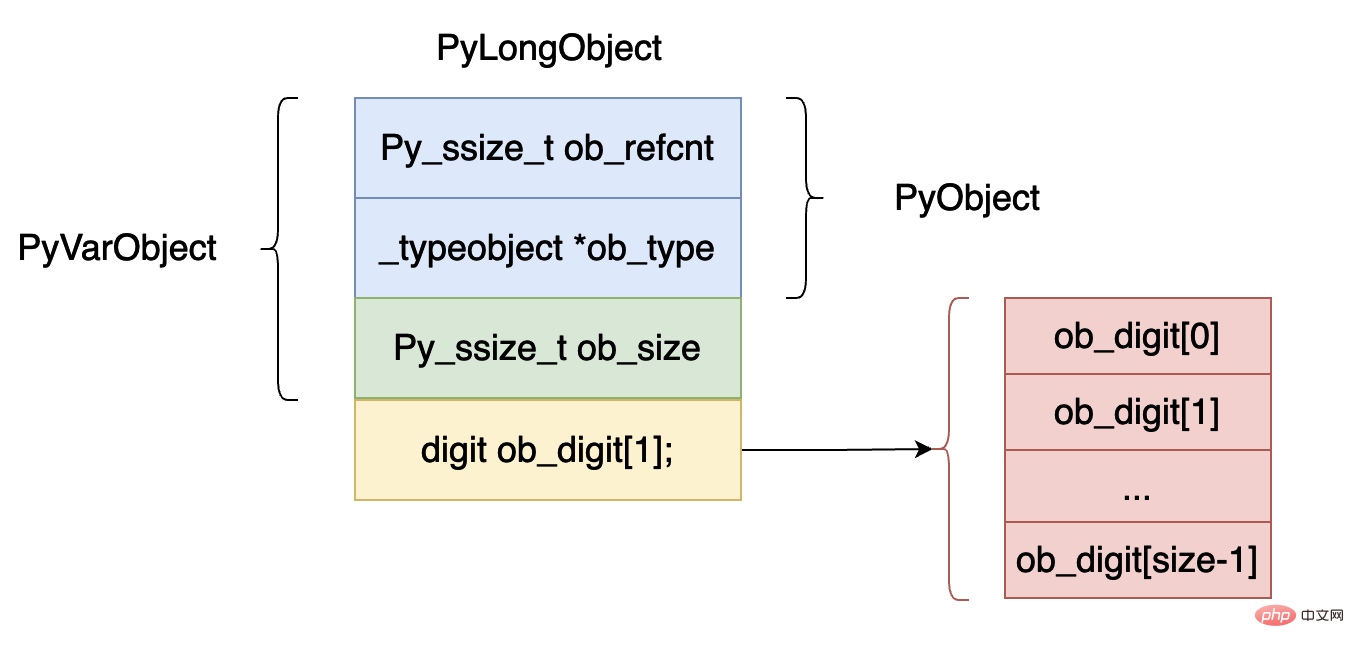
ob_refcnt, das die Referenz des Objekts The darstellt Die Anzahl der Zählungen ist für die Garbage Collection sehr nützlich. Später werden wir den Garbage Collection-Teil der virtuellen Maschine eingehend analysieren.
ob_type gibt den Datentyp dieses Objekts an. In Python ist es manchmal erforderlich, den Datentyp der Daten zu beurteilen. Beispielsweise werden die beiden Schlüsselwörter isinstance und type verwendet.
ob_size, dieses Feld gibt an, wie viele Elemente es in diesem ganzzahligen Objektarray ob_digit gibt. Der Typ
digit ist eigentlich eine Makrodefinition des Typs uint32_t, die 32-Bit-Ganzzahldaten darstellt.
Zunächst wissen wir, dass Ganzzahlen in Python nicht überlaufen, weshalb PyLongObject Arrays verwendet. In der internen Implementierung von cpython umfassen Ganzzahlen 0, positive Zahlen und negative Zahlen:
ob_size, das die Länge des Arrays speichert, wenn ob_size größer als 0 ist. Es speichert positive Zahlen. Wenn ob_size kleiner als 0 ist, wird eine negative Zahl gespeichert.
ob_digit, speichert den absoluten Wert der Ganzzahl. Wie wir bereits erwähnt haben, handelt es sich bei ob_digit um 32-Bit-Daten, aber nur die ersten 30 Bits werden intern in cpython verwendet, nur um Überlaufprobleme zu vermeiden.
Lassen Sie uns einige Beispiele verwenden, um die oben genannten Regeln im Detail zu verstehen:
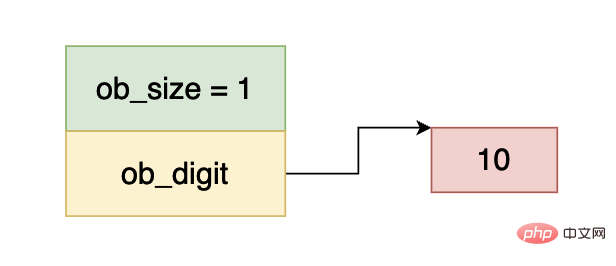
Im obigen Bild ist ob_size größer als 0, was darauf hinweist, dass diese Zahl eine positive Zahl ist, und ob_digit zeigt auf int32-Daten. Der Wert der Zahl ist gleich 10, daher stellt die obige Zahl die ganze Zahl 10 dar.
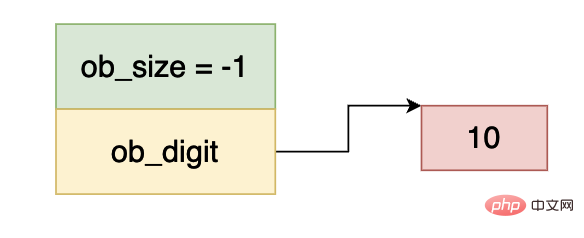
In ähnlicher Weise ist ob_size kleiner als 0 und ob_digit gleich 10, sodass die Daten im obigen Bild -10 darstellen.

Das Obige ist ein Beispiel für ein ob_digit-Array mit der Länge 2. Die oben dargestellten Daten lauten wie folgt:
1⋅20+1⋅21+1⋅22+. .. +1⋅229+0⋅230+0⋅231+1⋅232
Denn für jedes Array-Element verwenden wir nur die ersten 30 Bits, also bis zur zweiten Ganzzahl Die Daten entsprechen 230. Sie können den gesamten Berechnungsprozess anhand der obigen Ergebnisse verstehen.

Das Obige ist ganz einfach:
−(1⋅20+1⋅21+1⋅22+...+1⋅229+0&sdot ; 230+0⋅231+1⋅232)
Um die häufige Erstellung häufig verwendeter Ganzzahlen zu vermeiden und die Programmausführung zu beschleunigen, können wir den Cache für einige häufig verwendete Ganzzahlen verwenden Bitte überprüfen Sie es zuerst und geben Sie die Daten bei Bedarf direkt zurück. Der relevante Code in cpython lautet wie folgt: (Das Intervall der zwischengespeicherten Daten im kleinen Ganzzahlpool beträgt [-5, 256])
#define NSMALLPOSINTS 257 #define NSMALLNEGINTS 5 static PyLongObject small_ints[NSMALLNEGINTS + NSMALLPOSINTS];
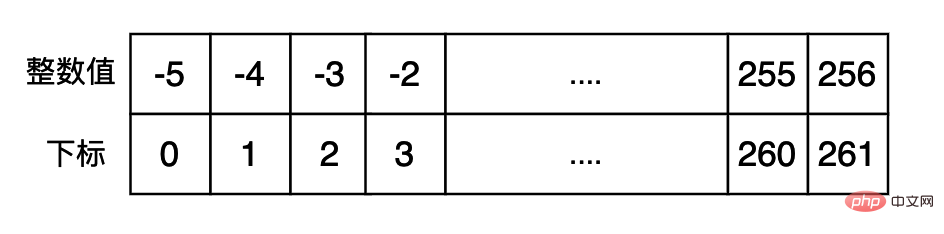
Wir verwenden den folgenden Code, um zu testen, ob der kleine Ganzzahlpool verwendet wird Wenn Daten verwendet werden, ist der Rückgabewert ihrer id() für die Daten im kleinen Ganzzahlpool derselbe. Die integrierte Funktion id gibt die Speicheradresse des Python-Objekts zurück.
>>> a = 1 >>> b = 2 >>> c = 1 >>> id(a), id(c) (4343136496, 4343136496) >>> a = -6 >>> c = -6 >>> id(a), id(c) (4346020624, 4346021072) >>> a = 257 >>> b = 257 >>> id(a), id(c) (4346021104, 4346021072) >>>
Was wir aus den obigen Ergebnissen sehen können, ist, dass für die Werte im Intervall [-5, 256] der Rückgabewert von id tatsächlich derselbe ist und der Rückgabewert außerhalb dieses Intervalls unterschiedlich ist.
Mit dieser Funktion können wir auch einen kleinen Trick implementieren, der darin besteht, den von einem PyLongObject-Objekt belegten Speicherplatz zu ermitteln, da wir die erste Speicheradresse der beiden Daten -5 und 256 verwenden und diese Adressen dann subtrahieren können die Größe des von 261 PyLongObjects belegten Speicherplatzes (beachten Sie, dass der kleine Ganzzahlpool zwar 262 Daten enthält, die letzten Daten jedoch die erste Adresse des Speichers und nicht die letzte Adresse sind, sodass nur 261 Daten vorhanden sind). Wir können die Speichergröße des PyLongObject-Objekts finden.
>>> a = -5 >>> b = 256 >>> (id(b) - id(a)) / 261 32.0 >>>
Aus der obigen Ausgabe können wir ersehen, dass ein PyLongObject-Objekt 32 Bytes belegt. Mit dem folgenden C-Programm können wir den tatsächlich von einem PyLongObject belegten Speicherplatz anzeigen.
#include "Python.h"
#include <stdio.h>
int main()
{
printf("%ld\n", sizeof(PyLongObject));
return 0;
}Die Ausgabe des obigen Programms lautet wie folgt:

Die beiden oben genannten Ergebnisse sind gleich, sodass unsere Idee ebenfalls bestätigt ist.
Der Kerncode zum Abrufen von Daten aus dem kleinen Ganzzahlpool lautet wie folgt:
static PyObject *
get_small_int(sdigit ival)
{
PyObject *v;
assert(-NSMALLNEGINTS <= ival && ival < NSMALLPOSINTS);
v = (PyObject *)&small_ints[ival + NSMALLNEGINTS];
Py_INCREF(v);
return v;
}如果你了解过大整数加法就能够知道,大整数加法的具体实现过程了,在 cpython 内部的实现方式其实也是一样的,就是不断的进行加法操作然后进行进位操作。
#define Py_ABS(x) ((x) < 0 ? -(x) : (x)) // 返回 x 的绝对值
#define PyLong_BASE ((digit)1 << PyLong_SHIFT)
#define PyLong_MASK ((digit)(PyLong_BASE - 1))
static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
// 首先获得两个整型数据的 size
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
PyLongObject *z;
Py_ssize_t i;
digit carry = 0;
// 确保 a 保存的数据 size 是更大的
/* Ensure a is the larger of the two: */
if (size_a < size_b) {
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
// 创建一个新的 PyLongObject 对象,而且数组的长度是 size_a + 1
z = _PyLong_New(size_a+1);
if (z == NULL)
return NULL;
// 下面就是整个加法操作的核心
for (i = 0; i < size_b; ++i) {
carry += a->ob_digit[i] + b->ob_digit[i];
// 将低 30 位的数据保存下来
z->ob_digit[i] = carry & PyLong_MASK;
// 将 carry 右移 30 位,如果上面的加法有进位的话 刚好可以在下一次加法当中使用(注意上面的 carry)
// 使用的是 += 而不是 =
carry >>= PyLong_SHIFT; // PyLong_SHIFT = 30
}
// 将剩下的长度保存 (因为 a 的 size 是比 b 大的)
for (; i < size_a; ++i) {
carry += a->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
// 最后保存高位的进位
z->ob_digit[i] = carry;
return long_normalize(z); // long_normalize 这个函数的主要功能是保证 ob_size 保存的是真正的数据的长度 因为可以是一个正数加上一个负数 size 还变小了
}
PyLongObject *
_PyLong_New(Py_ssize_t size)
{
PyLongObject *result;
/* Number of bytes needed is: offsetof(PyLongObject, ob_digit) +
sizeof(digit)*size. Previous incarnations of this code used
sizeof(PyVarObject) instead of the offsetof, but this risks being
incorrect in the presence of padding between the PyVarObject header
and the digits. */
if (size > (Py_ssize_t)MAX_LONG_DIGITS) {
PyErr_SetString(PyExc_OverflowError,
"too many digits in integer");
return NULL;
}
// offsetof 会调用 gcc 的一个内嵌函数 __builtin_offsetof
// offsetof(PyLongObject, ob_digit) 这个功能是得到 PyLongObject 对象 字段 ob_digit 之前的所有字段所占的内存空间的大小
result = PyObject_MALLOC(offsetof(PyLongObject, ob_digit) +
size*sizeof(digit));
if (!result) {
PyErr_NoMemory();
return NULL;
}
// 将对象的 result 的引用计数设置成 1
return (PyLongObject*)PyObject_INIT_VAR(result, &PyLong_Type, size);
}
static PyLongObject *
long_normalize(PyLongObject *v)
{
Py_ssize_t j = Py_ABS(Py_SIZE(v));
Py_ssize_t i = j;
while (i > 0 && v->ob_digit[i-1] == 0)
--i;
if (i != j)
Py_SIZE(v) = (Py_SIZE(v) < 0) ? -(i) : i;
return v;
}Das obige ist der detaillierte Inhalt vonWas ist das Implementierungsprinzip von Ganzzahlen in der virtuellen Python-Maschine?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




