So implementieren Sie die binäre Suche in Java

Binäre Suche

Übersicht

Die binäre Suche wird auch als binäre Suche (Binary Search) bezeichnet und ist eine effizientere Suchmethode.

Die binäre Suche erfordert jedoch, dass die lineare Tabelle eine sequentielle Speicherstruktur annimmt und die Elemente in der Tabelle nach Schlüsselwörtern geordnet werden müssen.

Merge-Sortierung verwendet die Idee der Dichotomie. Zuerst benötigen Sie ein Array, das von klein nach groß sortiert ist. Wenn es größer ist als das, was Sie suchen, suchen Sie nach vorne und suchen Sie dann nach dem mittleren Wert.

Wenn es kleiner ist als das, was Sie suchen, suchen Sie rückwärts, nehmen Sie die Hälfte nach dem Mittelwert und nehmen Sie dann den Mittelwert und vergleichen Sie.

Rekursive Implementierung

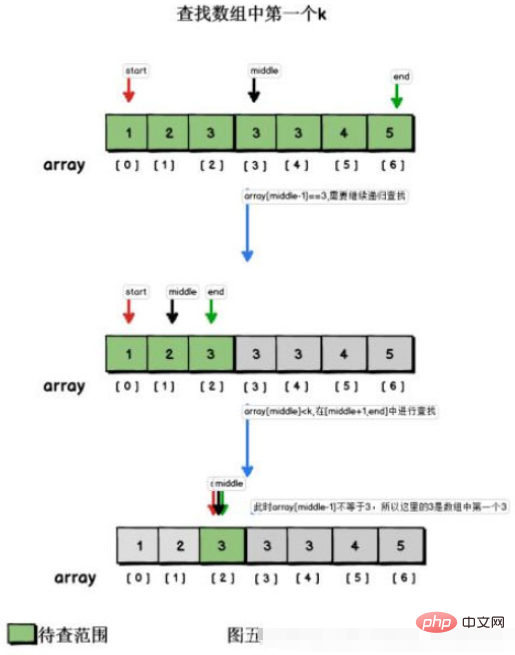
Hier habe ich die rekursive Methode zur Implementierung verwendet.

Zunächst müssen Sie den Suchbereich bestätigen, das heißt, es gibt einen linken Index und einen rechten Index. Jedes Mal wird (links+rechts)/2 als mittlerer Wert und die Größe des Elements verwendet Der zu durchsuchende Wert und der mittlere Wert werden verglichen. Wenn der mittlere Wert groß ist, wird mit der Suche vorwärts fortgefahren, d. h. der Rekursionsbereich liegt links und in der Mitte von 1. Andernfalls suchen Sie nach rechts, d. h. im rekursiven Bereich Mitte + 1, rechts. Wenn sie gleich sind, ist es gefunden.

Aber Sie müssen weiterhin vor und nach diesem Index suchen, um festzustellen, ob es einen gleichen Wert gibt, ihn zur Menge hinzufügen und schließlich diese Menge zurückgeben.

Rekursiver Implementierungscode

package search;
import java.util.ArrayList;
import java.util.List;
public class BinarySearch {
    public static void main(String[] args) {
        int[] array = {1,1,1,2,3,4,5,6,7};
        List<Integer> integers = binarySearch(array, 0, array.length - 1, 1);
//        for (Integer integer : integers) {
//            System.out.print(integer+ " ");
//        }
        System.out.println(integers);
    }
    public static List<Integer> binarySearch(int[] array, int left, int right, int value){
        //如果左索引大于右索引，则说明全部遍历完了，也没有找到相应的值，返回空集合即可
        if (left>right){
            return new ArrayList<Integer>();
        }
        //获取中间值的下标（二分）
        int mid = (left+right)/2;
        //如果要找的值比中间值小，则继续向左找
        if (value < array[mid]){
            return binarySearch(array, left, mid-1, value);
        //要找的值比中间值小大，则向右找
        }else if (value > array[mid]){
            return binarySearch(array, mid+1, right, value);
        //否则，说明相等，找到了
        }else {
            //找到一个，还需要向左右找找看有没有相同的值
            List<Integer> resultList = new ArrayList();
            //向左循环找，如果有，则加入到集合中
            int temp = mid - 1;
            while (temp>=0 && array[temp] == value){
                resultList.add(temp);
                temp -= 1;
            }
            //向右循环找，如果有，则加入到集合中
            temp = mid + 1;
            while (temp < array.length && array[temp] == value){
                resultList.add(temp);
                temp += 1;
            }
            //将一开始找到的那个索引页加入到集合中。
            resultList.add(mid);
            return resultList;
        }
    }
    
    //以下这段代码来自百度百科，供大家参考。
    public static int binarySearch(Integer[] srcArray, int des) {
        //定义初始最小、最大索引
        int start = 0;
        int end = srcArray.length - 1;
        //确保不会出现重复查找，越界
        while (start <= end) {
            //计算出中间索引值
            int middle = (end + start)>>>1 ;//防止溢出
            if (des == srcArray[middle]) {
                return middle;
                //判断下限
            } else if (des < srcArray[middle]) {
                end = middle - 1;
                //判断上限
            } else {
                start = middle + 1;
            }
        }
        //若没有，则返回-1
        return -1;
    }
}

Loop-Implementierungscode (nicht rekursiv)

package search;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
 * @Author: sshdg
 * @Date: 2020/9/21 9:22
 */
public class BinarySearch3 {
    public static void main(String[] args) {
        int[] array = {1,1,1,1,1,2,3,4,5,6,7};
        System.out.println(BinarySearch3.binarySearch(array, 7));
    }
    public static List<Integer> binarySearch(int[] array, int key){
        List<Integer> resultList = new ArrayList<>();
        int start = 0;
        int end = array.length - 1;
        while (start <= end){
            int mid = (start + end) / 2;
            int midValue = array[mid];
            if (key > midValue){
                //key比中间值大。向右找
                start = mid + 1;
            } else if (key < midValue){
                //key比中间值小。向左找
                end = mid - 1;
            } else {
                //否则就找到了
                //先向左找有没有相同值
                int temp = mid -1;
                while (temp >= start && array[temp] == key){
                    resultList.add(temp);
                    temp -= 1;
                }
                //将一开始找到的加入结果集
                resultList.add(mid);
                //再向右找找有没有相同值
                temp = mid + 1;
                while (temp <= end && array[temp] == key){
                    resultList.add(temp);
                    temp += 1;
                }
                break;
            }
        }
        return resultList;
    }
}

Binäre Suche (rekursiv, Schleife)

public class BinarySearch {
    /**
     * @author JadeXu
     * @// TODO: 2020/12/7 二分查找
     * 思路：
     * 1、获取数组的中间值，先获取下标，方便多次查找
     * 奇数位的数组直接获取中间位，偶数位的数组获取中间的第一位或第二位都可，一般获取第一位（因为与奇数位获取中间值的方法一样）
     * 2、获取查找的区间范围，start：区间开始的下标，end：区间结束的下标
     * 3、判断查找的数和中间位的数是否相同
     * 相同时，直接返回需要的数据，跳出方法
     * 大于时，即数可能在中间值右边的区间内，此时start = mid+1，即mid往后移一位，就得到了中间值右边区间的开始下标
     * 小于时，即数可能在中间值左边的区间内，此时end = mid-1，即mid往前移一位，就得到了中间值左边区间的结束下标
     * 当一个区间里，开始下标小于等于结束下标时，该区间才是有效区间，才能继续查找。否则无效，返回找不到，跳出方法
     */
    //循环
    /**
     * @param arr 已经升序好的int[]
     * @param num 需要查找的数字
     * @return 找到则返回下标，没找到则返回-1
     */
    private static int binarySearchByCycle(int[] arr,int num) {
        int start = 0;
        int end = arr.length - 1;
        while (start <= end){
            int mid = (start + end) / 2;
            if(num == arr[mid]){
                return mid;
            }else if(num > arr[mid]){
                start = mid + 1;
            }else {
                end = mid - 1;
            }
        }
        return -1;
    }
    //递归
    /**
     * @param arr 已经升序好的int[]
     * @param num 需要查找的数字
     * @param start 区间开始下标
     * @param end 区间结束下标
     * @return 找到则返回下标，没找到则返回-1
     */
    private static int binarySearchByRecursion(int[] arr,int num,int start,int end) {
        int mid = (start + end) / 2;
        if(num == arr[mid]){
            return mid;
        }else if(num > arr[mid]){
            start = mid + 1;
        }else {
            end = mid - 1;
        }
        if(start <= end){
            mid = binarySearchByRecursion(arr,num,start,end);  //递归继续寻找
        }else {
            mid = -1;
        }
        return mid;
    }
}

Das obige ist der detaillierte Inhalt vonSo implementieren Sie die binäre Suche in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!