 Java
Java
 javaLernprogramm
javaLernprogramm
 So passen Sie das Klassenkapselungsarray in Java an, um Datenoperationen zu implementieren
So passen Sie das Klassenkapselungsarray in Java an, um Datenoperationen zu implementieren
So passen Sie das Klassenkapselungsarray in Java an, um Datenoperationen zu implementieren
Als grundlegende Datenspeicherstruktur werden Arrays häufig verwendet. Array ist eine Datenstruktur, die kontinuierlichen Speicherplatz verwendet, um feste Länge und denselben Datentyp zu speichern. Die Datenstruktur ist sprachunabhängig. Hier wird Java zur Durchführung von Array-bezogenen Operationen verwendet. Array-Indizes beginnen bei 0.
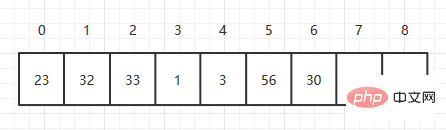
Eine Array-Initialisierung
Es gibt zwei Möglichkeiten, Daten zu erstellen. Eine besteht darin, zunächst Daten mit fester Länge zu deklarieren dann Weisen Sie dem Array dann einen Wert zu, und die andere besteht darin, einen Wert direkt zuzuweisen.
Der erste Typ:
数据类型[] 数组名称 = new 数据类型[长度];
Die Markierung [] hier deklariert ein Array. Dieses [] kann nach dem Datentyp platziert werden. kann mit dem gleichen Effekt auch nach dem Array-Substantiv platziert werden. Wenn ich ein Array vom Typ long mit einer Länge von 2 deklariere und einen Wert zuweise: 2的long类型的数组,并赋值:
long[] arr = new long[2]; arr[0] = 1; arr[1] = 2;
第二种:
数据类型[] 数组名称 = {元素1,元素2, ...};这样在数组初始化的时候直接给数组赋值,数组的长度由元素的个数决定。
二 自定义类封装数组实现数据操作
public class MyArray {
// 自定义数组 private long[] arr;
// 有效数据长度 private int element;
public MyArray(){
arr = new long[9];
}
public MyArray(int maxsize){
arr = new long[maxsize];
}
/**
* 显示数组元素
*/ public void display(){
System.out.print("[");
for (int i = 0; i < element; i++) {
System.out.print(arr[i]+" ");
}
System.out.print("]");
}
}2.1 添加元素
数组是用连续的内存空间来存储数据的,则每次添加的时候会往当前数组的最后一个元素上添加元素,一次就可以加上元素,所以它的复杂度为O(1),假如定义一个长度为9数组,数组中已经有两个元素,则添加第三个元素如下:
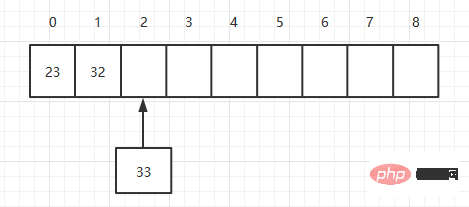
public void add(long value){
arr[element] = value;
element++;
}2.2 根据值查询元素位置
这种查找方式也叫做线性查找,就是根据传入的值循环去遍历元素,来获取对应的位置,理论上平均查询一个元素需要花费N/2次,所以它的复杂度为O(N)。
public int find(long value){
int i;
for (i = 0; i < element; i++) {
if(value == arr[i]){
break;
}
}
if(i == element){
return -1;
}else {
return i;
}
}2.3 根据索引查询元素
根据索引来查找元素,也就是获取对应位置的元素,其复杂度为O(1)。
public long get(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
return arr[index];
}
}2.4 根据索引删除元素
删除对应索引的元素后,我们需要将所有改索引后面的元素,向前移动一位。假如我要删除索引为2的元素,如下:
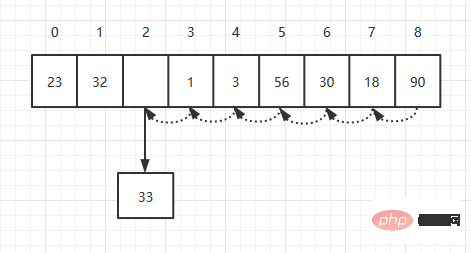
理论上平均删除一个元素,我们需要移动N/2次,所以它的时间复杂度也为O(N)。
public void delete(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
for (int i = index; i < element; i++) {
arr[index] = arr[index+1];
}
element --;
}
}2.5 修改元素
修改某个位置的元素,直接根据索引就一次就可以修改对应的元素,所以它的时间复杂度为O(1)。
public void change(int index,long newValue){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
arr[index] = newValue;
}
}三 有序数组
有序数组是数组的一种特殊类型,有序数组中的元素按照某种顺序进行排列。
3.1 添加元素
在添加元素的时候,将元素按顺序添加到某个位置。如下,在一个数组中添加一个33的元素。
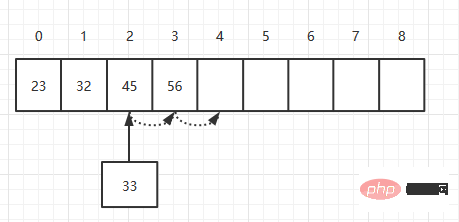
首先,将索引为3的元素移动到索引为4的位置,然后将索引为2的元素移动到索引为3的位置,最后将33添加到索引为2的位置。理论上插入一个元素需要移动元素的个数为N/2个,所以它的时间复杂度为O(N)。
public void add(long value){
int i;
for (i = 0; i < element; i++) {
if(arr[i]>value){
break;
}
}
for (int j = element; j > i; j--){
arr[j] = arr[j-1];
}
arr[i] = value;
element++;
}3.2 二分法根据元素查询索引
在无序数组中,使用线性法进行查找相关元素,线性法即按索引按个查找。有序数组可以使用二分法来查找元素,二分法是指将一个数组从中间分成两个,判断元素位于哪个数组中,然后重复这样的操作。
假如有8
public int search(long value){
// 中间值 int middle = 0;
// 最小值 int low = 0;
// 最大值 int pow = element;
while (true){
middle = (low + pow) / 2;
if(arr[middle] == value){
return middle;
}else if (low > pow){
return -1;
}else{
if(arr[middle] > value){
pow = middle - 1;
}else{
low = middle + 1;
}
}
}
}Zweiter Typ#🎜🎜 # :
rrreeeAuf diese Weise wird dem Array direkt bei der Initialisierung ein Wert zugewiesen. Die Länge des Arrays wird durch die Anzahl der Elemente bestimmt.
| Arrays verwenden kontinuierlichen Speicherplatz, um Daten zu speichern, und zwar jedes Mal Wird ein Element hinzugefügt, wird es zum letzten Element des aktuellen Arrays hinzugefügt. Die Komplexität beträgt also O(1), wenn Sie ein Array mit einer Länge von | |
|---|---|
| rrreee | 2.3 Elemente basierend auf dem Index abfragenUm Elemente basierend auf dem Index zu finden, dh um das Element an der entsprechenden Position zu erhalten, beträgt die Komplexität O(1). |
| Nachdem wir das dem Index entsprechende Element gelöscht haben, müssen wir alle Elemente nach dem Index um eine Position nach vorne verschieben. Wenn ich das Element mit Index 2 löschen möchte, wie folgt: | |
| rrreee | 2.5 Elemente ändernÄndern Sie das Element an einer bestimmten Position und ändern Sie das entsprechende Element einmal direkt entsprechend dem Index, sodass seine zeitliche Komplexität O(1) ist. |
| Geordnetes Array ist eine besondere Art von Array. Die Elemente im geordneten Array sind in einer bestimmten Reihenfolge angeordnet. | 3.1 Elemente hinzufügen |
| Zuerst hinzufügen Das Element bei Index 3 wird auf Index 4 verschoben, dann wird das Element bei Index 2 auf Index 3 verschoben und schließlich wird 33 zu Index 2 hinzugefügt. Theoretisch erfordert das Einfügen eines Elements das Verschieben von N/2 Elementen, sodass seine Zeitkomplexität O(N) beträgt. | |
| Verwenden Sie in einem ungeordneten Array die lineare Methode, um verwandte Elemente nacheinander zu finden zum Index. Sortierte Arrays können die Dichotomiemethode verwenden, um Elemente zu finden. Dichotomie bedeutet, ein Array von der Mitte aus in zwei Teile zu teilen, zu bestimmen, in welchem Array sich das Element befindet, und diesen Vorgang dann zu wiederholen. | Wenn es ein Array mit |
- Je geringer die Komplexität, desto besser ist O(1) > O(N) > N^2).
- AlgorithmusKomplexität
Das obige ist der detaillierte Inhalt vonSo passen Sie das Klassenkapselungsarray in Java an, um Datenoperationen zu implementieren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1384
1384
 52
52
 Perfekte Zahl in Java
Aug 30, 2024 pm 04:28 PM
Perfekte Zahl in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur perfekten Zahl in Java. Hier besprechen wir die Definition, Wie prüft man die perfekte Zahl in Java?, Beispiele mit Code-Implementierung.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden für Weka in Java. Hier besprechen wir die Einführung, die Verwendung von Weka Java, die Art der Plattform und die Vorteile anhand von Beispielen.
 Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur Smith-Zahl in Java. Hier besprechen wir die Definition: Wie überprüft man die Smith-Nummer in Java? Beispiel mit Code-Implementierung.
 Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
In diesem Artikel haben wir die am häufigsten gestellten Fragen zu Java Spring-Interviews mit ihren detaillierten Antworten zusammengestellt. Damit Sie das Interview knacken können.
 Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Java 8 führt die Stream -API ein und bietet eine leistungsstarke und ausdrucksstarke Möglichkeit, Datensammlungen zu verarbeiten. Eine häufige Frage bei der Verwendung von Stream lautet jedoch: Wie kann man von einem Foreach -Betrieb brechen oder zurückkehren? Herkömmliche Schleifen ermöglichen eine frühzeitige Unterbrechung oder Rückkehr, aber die Stream's foreach -Methode unterstützt diese Methode nicht direkt. In diesem Artikel werden die Gründe erläutert und alternative Methoden zur Implementierung vorzeitiger Beendigung in Strahlverarbeitungssystemen erforscht. Weitere Lektüre: Java Stream API -Verbesserungen Stream foreach verstehen Die Foreach -Methode ist ein Terminalbetrieb, der einen Vorgang für jedes Element im Stream ausführt. Seine Designabsicht ist
 Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Anleitung zum TimeStamp to Date in Java. Hier diskutieren wir auch die Einführung und wie man Zeitstempel in Java in ein Datum konvertiert, zusammen mit Beispielen.
 Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Kapseln sind dreidimensionale geometrische Figuren, die aus einem Zylinder und einer Hemisphäre an beiden Enden bestehen. Das Volumen der Kapsel kann berechnet werden, indem das Volumen des Zylinders und das Volumen der Hemisphäre an beiden Enden hinzugefügt werden. In diesem Tutorial wird erörtert, wie das Volumen einer bestimmten Kapsel in Java mit verschiedenen Methoden berechnet wird. Kapselvolumenformel Die Formel für das Kapselvolumen lautet wie folgt: Kapselvolumen = zylindrisches Volumenvolumen Zwei Hemisphäre Volumen In, R: Der Radius der Hemisphäre. H: Die Höhe des Zylinders (ohne die Hemisphäre). Beispiel 1 eingeben Radius = 5 Einheiten Höhe = 10 Einheiten Ausgabe Volumen = 1570,8 Kubikeinheiten erklären Berechnen Sie das Volumen mithilfe der Formel: Volumen = π × R2 × H (4
 Wie führe ich Ihre erste Spring -Boot -Anwendung in der Spring Tool Suite aus?
Feb 07, 2025 pm 12:11 PM
Wie führe ich Ihre erste Spring -Boot -Anwendung in der Spring Tool Suite aus?
Feb 07, 2025 pm 12:11 PM
Spring Boot vereinfacht die Schaffung robuster, skalierbarer und produktionsbereiteter Java-Anwendungen, wodurch die Java-Entwicklung revolutioniert wird. Der Ansatz "Übereinkommen über Konfiguration", der dem Feder -Ökosystem inhärent ist, minimiert das manuelle Setup, Allo





