So implementieren Sie den Arctan-Konvertierungswinkel in Python

Kartesisches Koordinatensystem

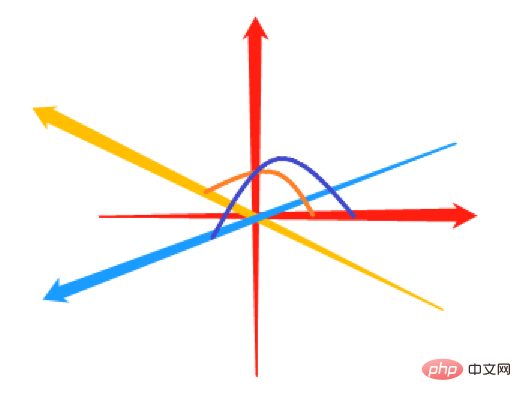
Für das ebene Koordinatensystem kann der Winkelbereich θ zwischen einem beliebigen Strahl OP und der x-Achse [0,2π) oder (-π,&pi) betragen ;] , sofern nicht anders angegeben, verwenden wir Letzteres
um den Punkt Pc = (x, y, z) im kartesischen Raumkoordinatensystem in die Form des sphärischen Koordinatensystems auszudrückenPs = ( θ , ϕ , r ) > θ的范围，可以取[0,2π)或者(-π,π]，如无特殊说明， 我们统一使用后者。
将笛卡尔空间坐标系中的点 Pc = ( x , y , z ) 表示成球体坐标系中的形式 Ps = ( θ , ϕ , r )。

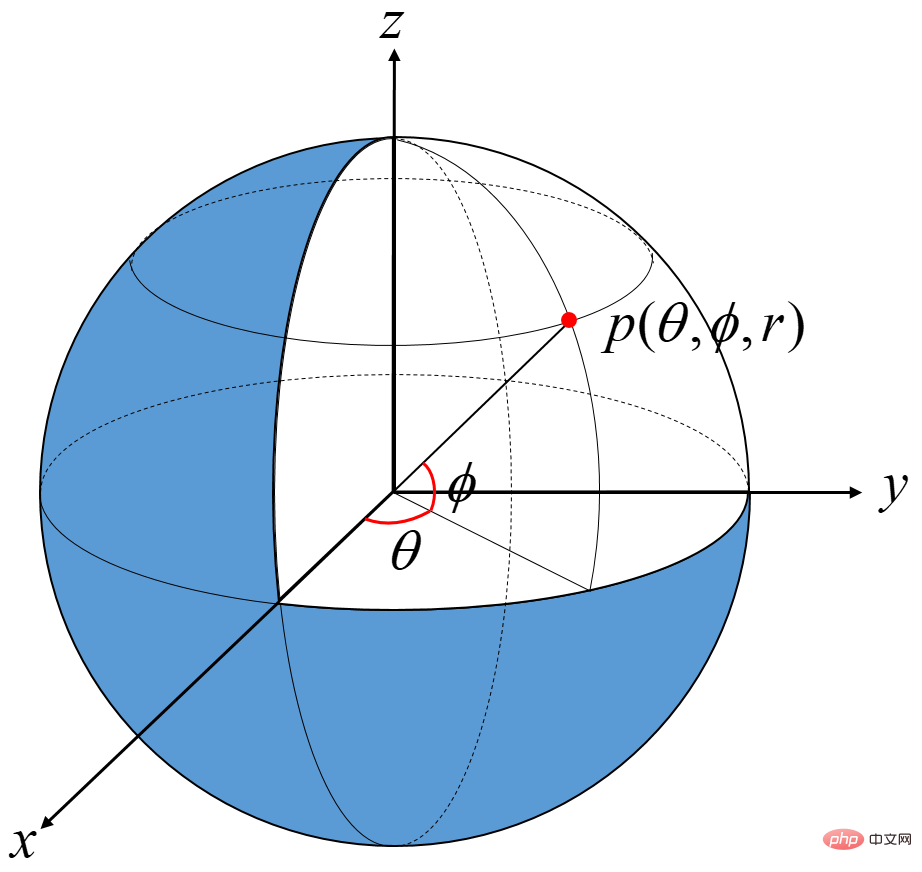
其中

根据球坐标的定义，要求θ∈[−π,π]，ϕ∈[−π/2,π/2] ，r∈[0 , +∞)。

对于 θ，正切函数的周期是 π，因此反正切函数 arctan 一般也只取一个周期，其定义域是 R，值域是(−π/2 , π/2) 。为了解决这个问题，引入了 Arctan 函数，也就是 arctan2 函数。

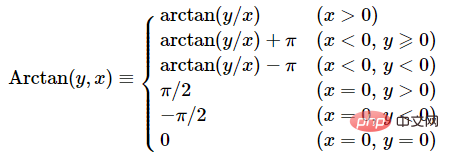
atan2 函数的使用 atan2(delta_y , delta_x)

import math
a = math.atan2(400,-692.820)
# 2.6179936760992044
angle = a/math.pi*180
# 149.99998843242386

atan 函数的使用 atan(delta_y / delta_x)

import math
delta_y = 400
delta_x = -692.820

if delta_x == 0:
    b = math.pi / 2.0
    angle = b/math.pi*180
    if delta_y == 0:
        angle = 0.0
    elif delta_y < 0:
        angle -= 180
else:
    b =  math.atan(delta_y/delta_x) 
    angle = b/math.pi*180
    if delta_y > 0 and delta_x < 0:
        angle = angle + 180
    if delta_y < 0 and delta_x < 0:
        angle = angle - 180

b,angle
# (-0.5235989774905888, 149.99998843242386)

atan 和 atan2 的异同

• 参数的个数不同

• 两者返回值都是弧度

• 如果 delta_x等于0，atan2依然可以计算，但是 atan 则需要提前判断，否则就会导致程序出错

• 象限的处理

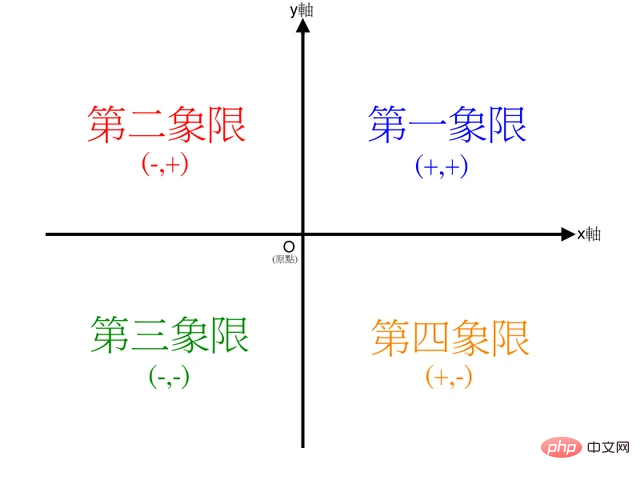
atan2(b,a)是4象限反正切，它的取值不仅取决于正切值b/a，还取决于点(b,a) 落入哪个象限：

• 当点 (b,a) 落入第一象限(b>0, a>0)时，atan2(b,a)的范围是 0 ~ pi/2

• 当点 (b,a)落入第二象限(b>0, a<0)时，atan2(b,a)的范围是 pi/2 ~ pi

• 当点 (b,a)落入第三象限(b<0, a<0)时，atan2(b,a)的范围是 -pi～-pi/2

• 当点 (b,a) 落入第四象限(b<0, a>0)时，atan2(b,a)的范围是 -pi/2～０

而 atan(b/a) 仅仅根据正切值为a/b求出对应的角度 (可以看作仅仅是2象限反正切)：

• 当 b/a > 0 时，atan(b/a)取值范围是 0 ~ pi/2

• 当 b/a < 0 时，atan(b/a)取值范围是 -pi/2～0

取值范围

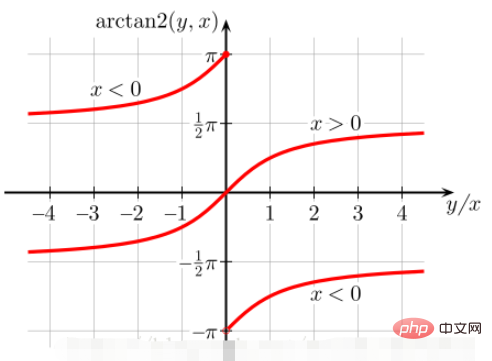
• 点 (b,a) 落入第一象限 (b>0, a>0)或 <code>第四象限(b<0, a>0)时，atan2(b,a) = atan(b/a)

• 点 (b,a) 落入第二象限 (b>0, a<0)，b/a<0，故atan(b/a)取值范围始终是 -pi/2～０，然而，atan2(b,a)的范围是 pi/2 ~ pi，故atan(b/a) 计算角度值要加180。

• 点 (b,a) 落入第三象限(b<0, a<0) ，b/a>0，故 atan(b/a) 取值范围是 0 ~ pi/2，而此时atan2(b,a)的范围是 -pi～-pi/2

  Unter ihnen

Gemäß der Definition von Kugelkoordinaten, θ ∈[−π,π], ϕ∈[−π/2,π/2], r∈[0, +∞). 🎜🎜Für θ ist die Periode der Tangensfunktion π, sodass die Arcustangensfunktion arctan im Allgemeinen nur eine Periode benötigt, ihr Definitionsbereich R ist und ihr Wertebereich (−π/ 2, π/2). Um dieses Problem zu lösen, wurde die Arctan-Funktion, auch bekannt als arctan2-Funktion, eingeführt. 🎜🎜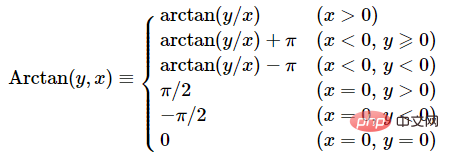🎜🎜atan2-Funktionsverwendung atan2(delta_y, delta_x)🎜rrreee🎜atan-Funktionsverwendung atan(delta_y / delta_x)🎜rrreee🎜Ähnlichkeiten und Unterschiede zwischen atan und atan2🎜

• 🎜Die Anzahl der Parameter ist unterschiedlich🎜🎜
• 🎜Der Rückgabewert von beiden ist das gleiche Bogenmaß🎜🎜
• 🎜Wenn delta_x gleich 0 ist, kann atan2 immer noch berechnet werden, aber atan muss im Voraus beurteilt werden, sonst kommt es zu Programmfehlern🎜🎜
• 🎜Quadrantenverarbeitung🎜🎜🎜🎜 🎜🎜atan2(b,a) ist der 4-Quadranten-Arkustangens. Sein Wert nicht hängt nur vom Tangenswert b/a ab, hängt auch davon ab, in welchen Quadranten der Punkt (b, a) fällt: 🎜
  • 🎜Wenn der Punkt (b, a) Fällt in den ersten Quadranten (b>0, a> ;0), beträgt der Bereich von atan2(b,a) 0 ~ pi/2🎜🎜
  • 🎜Wenn Punkt (b,a) Fällt in den zweiten Quadranten (b>0, a< ;0), beträgt der Bereich von atan2(b,a) pi/2 ~ pi🎜🎜
  • 🎜Wenn Punkt (b,a) Wenn Punkt (b, a) fällt in den vierten Quadranten (b<0 , a>0), der Bereich von atan2(b,a) ist -pi/2～0🎜🎜🎜🎜 und atan(b/a ) wird nur basierend auf dem Tangenswert von a/b berechnet. Der entsprechende Winkel (kann nur als Arcustangens der beiden Quadranten angesehen werden): 🎜
    • 🎜Wenn b /a > 0, der Wertebereich von atan(b/a) Es ist 0 ~ pi/2🎜🎜
    • 🎜Wenn b/a < b/a) ist -pi/2～0</code >🎜🎜🎜🎜Wertebereich🎜🎜<img src="https://img.php.cn/upload/article/000/887/227 /168189146627107.png"/ alt="So implementieren Sie den Arctan-Konvertierungswinkel in Python" >🎜🎜<img src="https: //img.php.cn/upload/article/000/887/227/168189146672211.png"/ alt="So implementieren Sie den Arctan-Konvertierungswinkel in Python" >🎜<ul class=" list-paddingleft- 2"><li>🎜Punkt (b,a) fällt in< When code>Der erste Quadrant (b>0, a>0) oder <code>Der vierte Quadrant (b<0, a>0). ), atan2(b,a) = atan(b/a) 🎜🎜
    • 🎜Punkt (b,a) fällt in den zweiten Quadranten (b>0, a<0), b/a<0, Daher ist der Wertebereich von atan(b/a) immer -pi/2~0. b,a) ist pi/2 ~ pi Daher müssen 180 zum durch atan(b/a) berechneten Winkelwert addiert werden. 🎜🎜
    • 🎜Punkt (b,a) fällt in den dritten Quadranten (b<0, a<0), b/a>0, also der Wertebereich von atan(b/a ) ist 0 ~ pi/2, und zu diesem Zeitpunkt ist der Bereich von atan2(b,a) -pi~-pi/2, also atan(b/a ) berechnet den Winkel. Der Wert wird um 180 reduziert. 🎜🎜🎜🎜Fazit: atan- und atan2-Funktionen. Es wird empfohlen, die atan2-Funktion zu verwenden🎜

Das obige ist der detaillierte Inhalt vonSo implementieren Sie den Arctan-Konvertierungswinkel in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!