So implementieren Sie eine vollständige Permutation im Java-Algorithmus

Algorithmus 1

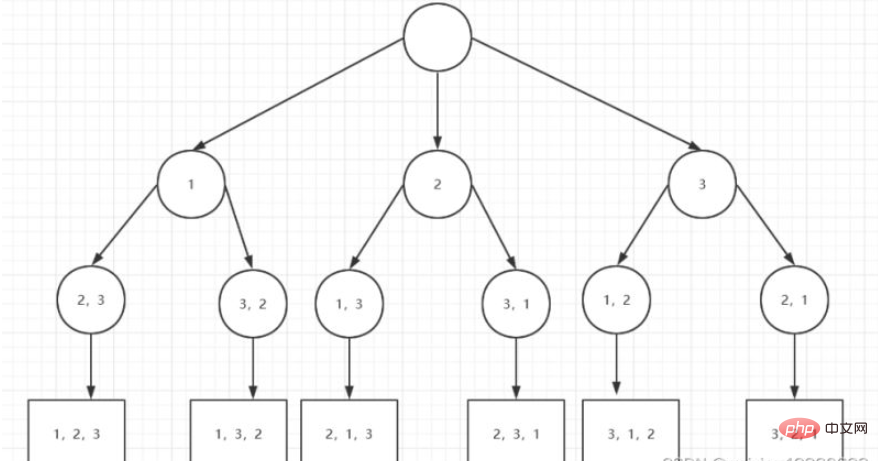
implementiert basierend auf Rekursion und Backtracking. Wenn Sie 1, 2 und 3 anordnen, gehen Sie zunächst von 3 zu 2 zurück und stellen Sie fest, dass es keine anderen möglichen Situationen gibt. Gehen Sie dann zu 1 zurück, ordnen Sie 1, 3, 2 und gehen Sie dann zurück zu den anderen Situationen , also der Wurzelknoten, und dann Wenn Sie 2 als erste Position anordnen, wiederholen Sie den obigen Vorgang, um alle möglichen Ergebnisse in res einzufügen.

Code:

import java.util.ArrayList;
import java.util.List;
 
public class h718_1 {
 
    static List<List<Integer>> res = new ArrayList<>();
    public static void main(String[] args) {
        int[] arr = {1,2,3};
 
        h718_1 h2 = new h718_1();
        h2.dfs(arr,new ArrayList<>());
        for (List<Integer> re : res) {
            System.out.println(re);
        }
 
    }
 
    public List<List<Integer>> dfs( int[] arr,List<Integer> list){
        List<Integer> temp = new ArrayList<>(list);
        if (arr.length == list.size()){
            res.add(temp);
        }
        for (int i=0;i<arr.length;i++){
            if (temp.contains(arr[i])){
                continue;
            }
            temp.add(arr[i]);
            dfs(arr,temp);
            temp.remove(temp.size()-1);
        }
        return res;
    }
 
}

Algorithmus 2

Erzielen Sie eine vollständige Permutation durch Vertauschen der Positionen: Angenommen, die Menge ist {1, 2, 3, 4};

Zyklus vertauscht die Positionen: 1 und 1 werden vertauscht; 1 und 2 werden vertauscht; 1 und 3 werden vertauscht; 1 und 4 werden vertauscht; betrachtet als {1} + rekursiver Austausch {2,3,4};

Der erste Austausch von 1 und 2 bestimmt, dass 2 an erster Stelle steht, sodass er als {2} + rekursiver Austausch {1,3 betrachtet werden kann ,4};

Der erste Austausch von 1 mit 3 bestimmt, dass 3 an erster Stelle steht, sodass er als {3} + rekursiver Austausch {1,2,4} betrachtet werden kann;

Der erste Austausch von 1 und 4 bestimmt, dass 4 an erster Stelle steht, sodass es als {4 } + Rekursiver Austausch {1,2,3};

usw. angesehen werden kann.

Code:

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
 
public class h718_2 {
    static List<List<Integer>> res = new ArrayList<>();
    public static void main(String[] args) {
 
        int[] arr = {1,2,3};
        h718_2 h3 = new h718_2();
        h3.pailie_swap(0,arr);
 
    }
    public void pailie_swap(int index, int[] arr){
        if (arr.length==index){
            System.out.println(Arrays.toString(arr));
            return;
        }
        for (int i = index;i<arr.length;i++){
            swap(i,index,arr);
            pailie_swap(index+1,arr);
            swap(i,index,arr);
        }
 
    }
 
    public void swap(int i,int j ,int[] arr){
        int temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
 
    }
}

Algorithmus 3

Sie können eine vollständige Anordnung durch Hinzufügen von Elementen erreichen:

Zuerst eine Liste definieren und das erste Element darin einfügen. Anschließend fügen Sie die verbleibenden Elemente der Reihe nach an allen möglichen Positionen der zuvor festgelegten Elemente ein Erstellen Sie eine neue Liste.

Zum Beispiel: Um eine vollständige Anordnung von {1,2,3,4} zu erreichen, definieren Sie zunächst eine Liste und fügen Sie das erste Element als {1} hinzu. 1} Die beiden Positionen davor und danach bilden eine neue Liste: {21, 12}, und das dritte Element 3 wird an allen Positionen der Elemente der Liste eingefügt: {321, 231, 213, 312, 132, 123}; und so weiter.

Code:

import java.util.ArrayList;
 
public class h718_3 {
 
    public static void main(String[] args) {
        String aa = "123";
        h718_3 h4 = new h718_3();
        ArrayList<String> res = new ArrayList<>();
        res = h4.getPermutation0(aa);
 
        for (String re : res) {
            System.out.println(re);
        }
 
    }
 
    public ArrayList<String> getPermutation0(String A) {
        int n = A.length();
        ArrayList<String> res = new ArrayList<>();
        res.add(A.charAt(0) + "");//初始化,包含第一个字符
 
        for (int i = 1; i < n; i++) {//第二个字符插入到前面生成集合的每个元素里面
            ArrayList<String> res_new = new ArrayList<>();
            char c = A.charAt(i);//新字符
            for (String str : res) {//访问上一趟集合中的每个字符串
                //  插入到每个位置,形成一个新串
                String newStr = c + str;//加在前面
                res_new.add(newStr);
                newStr = str + c;//加在后面
                res_new.add(newStr);
                //加在中间
                for (int j = 1; j < str.length(); j++) {
                    newStr = str.substring(0, j) + c + str.substring(j);
                    res_new.add(newStr);
                }
            }
            res = res_new;//更新
 
        }
        return res;
    }
}

Das obige ist der detaillierte Inhalt vonSo implementieren Sie eine vollständige Permutation im Java-Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!