Beispielcodeanalyse für eine Java-BigDecimal-Klassenanwendung
1. Einführung
Das Hauptziel des Entwurfs von Float- und Double-Typen sind wissenschaftliche Berechnungen und technische Berechnungen. Sie führen binäre Gleitkommaoperationen durch, die sorgfältig entwickelt wurden, um schnelle Näherungsberechnungen mit hoher Genauigkeit über einen weiten Wertebereich zu ermöglichen. Sie liefern jedoch keine völlig genauen Ergebnisse und sollten nicht dort eingesetzt werden, wo genaue Ergebnisse erforderlich sind. Geschäftsberechnungen erfordern jedoch häufig genaue Ergebnisse, und BigDecimal erweist sich in diesem Fall als nützlich.
2. Einführung in Wissenspunkte
2. Konstruktionsmethode
3. Additions-, Subtraktions-, Multiplikations- und Divisionsoperationen
-
5. Zusammenfassung
- 6. Verfeinerungsübungen
- 3. Detaillierte Erklärung der WissenspunkteWarum BigDecimal verwenden?
Code-Demonstration:
package com.Test;
import Test2.MyDate;
import java.awt.*;
import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.Calendar;
import java.util.Date;
import java.util.GregorianCalendar;
import java.util.Properties;
public class Main {
private final static String name = "磊哥的java历险记-@51博客";
public static void main(String[] args) {
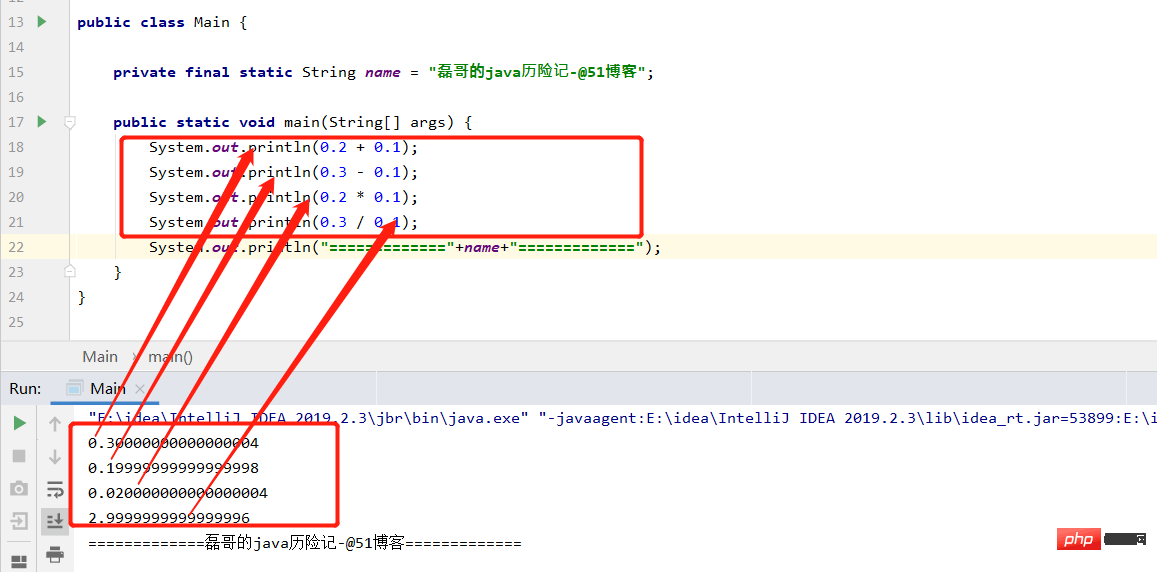
System.out.println(0.2 + 0.1);
System.out.println(0.3 - 0.1);
System.out.println(0.2 * 0.1);
System.out.println(0.3 / 0.1);
System.out.println("============="+name+"=============");
}
}Sie denken, Sie haben es falsch gesehen, aber das Ergebnis ist so. Was ist das Problem? Der Grund dafür ist, dass unsere Computer binär sind. Es gibt keine Möglichkeit, Gleitkommazahlen binär genau darzustellen. Unsere CPU stellt dar, dass Gleitkommazahlen aus zwei Teilen bestehen: Exponent und Mantisse. Diese Darstellungsmethode verliert im Allgemeinen einen gewissen Grad an Genauigkeit, und einige Gleitkommazahlenoperationen führen auch zu bestimmten Fehlern. Beispiel: Die binäre Darstellung von 2,4 ist nicht genau 2,4. Stattdessen ist die nächstliegende Binärdarstellung 2,3999999999999999. Der Wert einer Gleitkommazahl wird tatsächlich durch eine bestimmte mathematische Formel berechnet.
Tatsächlich kann Javas Float nur für wissenschaftliche Berechnungen oder technische Berechnungen verwendet werden. In den meisten kommerziellen Berechnungen wird die Klasse java.math.BigDecimal im Allgemeinen für präzise Berechnungen verwendet. 2. BigDecimal-Konstruktionsmethode in BigDecimal
(3) public BigDecimal(String val): String-Darstellung in BigDecimal konvertieren
Code-Demonstration:
package com.Test;
import Test2.MyDate;
import java.awt.*;
import java.math.BigDecimal;
import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.Calendar;
import java.util.Date;
import java.util.GregorianCalendar;
import java.util.Properties;
public class Main {
private final static String name = "磊哥的java历险记-@51博客";
public static void main(String[] args){
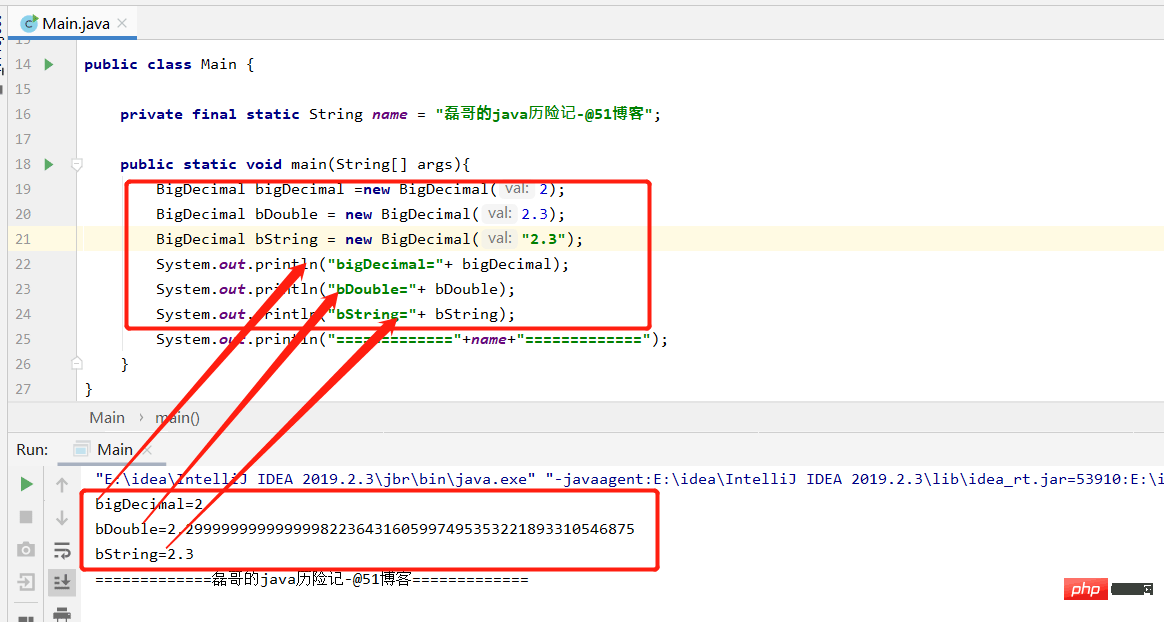
BigDecimal bigDecimal =new BigDecimal(2);
BigDecimal bDouble = new BigDecimal(2.3);
BigDecimal bString = new BigDecimal("2.3");
System.out.println("bigDecimal="+ bigDecimal);
System.out.println("bDouble="+ bDouble);
System.out.println("bString="+ bString);
System.out.println("============="+name+"=============");
}
}Nach dem Login kopieren
package com.Test;
import Test2.MyDate;
import java.awt.*;
import java.math.BigDecimal;
import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.Calendar;
import java.util.Date;
import java.util.GregorianCalendar;
import java.util.Properties;
public class Main {
private final static String name = "磊哥的java历险记-@51博客";
public static void main(String[] args){
BigDecimal bigDecimal =new BigDecimal(2);
BigDecimal bDouble = new BigDecimal(2.3);
BigDecimal bString = new BigDecimal("2.3");
System.out.println("bigDecimal="+ bigDecimal);
System.out.println("bDouble="+ bDouble);
System.out.println("bString="+ bString);
System.out.println("============="+name+"=============");
}
}- Die laufenden Ergebnisse sind wie folgt:
Warum passiert das?
3. Beschreibung des QuellcodesDas Ergebnis der Konstruktionsmethode mit Parametertyp double ist etwas unvorhersehbar. Man könnte meinen, dass das Schreiben von newBigDecimal(0.1) in Java ein BigDecimal erzeugt, das genau gleich 0,1 ist (der unskalierte Wert von 1, der eine Skalierung von 1 hat), aber es ist tatsächlich gleich 5. Dies liegt daran, dass 0,1 nicht exakt als Double (oder in diesem Fall als irgendeine binäre Dezimalzahl endlicher Länge) dargestellt werden kann. Auf diese Weise ist der an den Konstruktor übergebene Wert nicht genau gleich 0,1 (obwohl er scheinbar diesem Wert entspricht).
Der String-Konstruktor hingegen ist vollständig vorhersehbar: Durch das Schreiben von newBigDecimal("0.1") wird ein BigDecimal erstellt, das genau dem erwarteten 0,1 entspricht. Daher wird im Vergleich dazu generell empfohlen, den String-Konstruktor zu bevorzugen.
Wenn double als Quelle von BigDecimal verwendet werden muss, verwenden Sie bitte Double.toString(double), um in String zu konvertieren, und verwenden Sie dann den String-Konstruktor oder die statische Methode valueOf von BigDecimal
Code-Demonstration:
package com.Test;
import Test2.MyDate;
import java.math.BigDecimal;
public class Main {
private final static String name = "磊哥的java历险记-@51博客";
public static void main(String[] args) {
BigDecimal bDouble1 =BigDecimal.valueOf(2.3);
BigDecimal bDouble2 = new BigDecimal(Double.toString(2.3));
System.out.println("bDouble1="+ bDouble1);
System.out.println("bDouble2="+ bDouble2);
System.out.println("============="+name+"=============");
}
}Die Ergebnisse sind wie folgt:
4. BigDecimal-Additions-, Subtraktions-, Multiplikations- und Divisionsoperationen
Für häufig verwendete Additions-, Subtraktions-, Multiplikations- und Divisionsoperationen stellt die BigDecimal-Klasse entsprechende Mitgliedsmethoden bereit.
(1) public BigDecimal add(BigDecimal value); Addition
(2) public BigDecimal subtract(BigDecimal value); / /Multiplizieren Sie die Unteilbarkeit, z. B. 4,5/1,3, dann wird der Fehler java.lang.ArithmeticException:Non-terminating Decimal Expansion;No Exactable Representable Decimal Result angezeigt.
Tatsächlich kann die Divisionsmethode drei Parameter übergeben:
public BigDecimal divide(BigDecimal divisor, int scale, introundingMode) 第一参数表示除数, 第二个参数表示小数点后保留位数, 第三个参数表示舍入模式,只有在作除法运算或四舍五入时才用到舍入模式,有下面这几种
(1)ROUND_CEILING //向正无穷方向舍入
(2)ROUND_DOWN //向零方向舍入
(3)ROUND_FLOOR //向负无穷方向舍入
(4)ROUND_HALF_DOWN //向(距离)最近的一边舍入,除非两边(的距离)是相等,如果是这样,向下舍入, 例如1.55 保留一位小数结果为1.5
(5)ROUND_HALF_EVEN //向(距离)最近的一边舍入,除非两边(的距离)是相等,如果是这样,如果保留位数是奇数,使用ROUND_HALF_UP,如果是偶数,使用ROUND_HALF_DOWN
(6)ROUND_HALF_UP //向(距离)最近的一边舍入,除非两边(的距离)是相等,如果是这样,向上舍入, 1.55保留一位小数结果为1.6
(7)ROUND_UNNECESSARY //计算结果是精确的,不需要舍入模式
(8)ROUND_UP //向远离0的方向舍入
按照各自的需要,可传入合适的第三个参数。四舍五入采用 ROUND_HALF_UP
需要对BigDecimal进行截断和四舍五入可用setScale方法,例:
代码演示:
public static void main(String[] args) {
BigDecimal a = newBigDecimal("4.5635");
//保留3位小数,且四舍五入
a = a.setScale(3,RoundingMode.HALF_UP);
System.out.println(a);
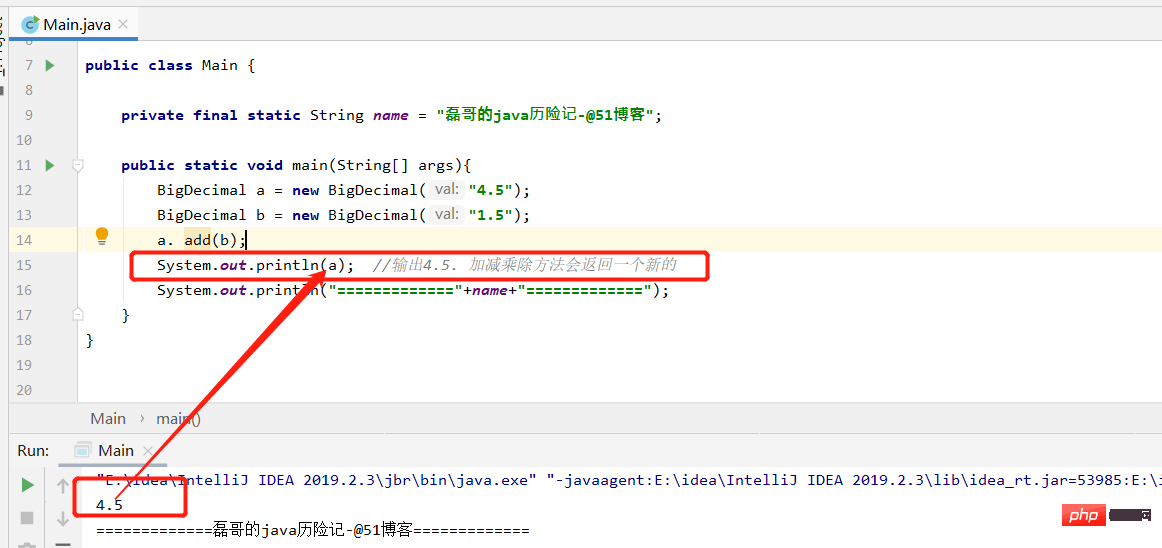
}注:减乘除其实最终都返回的是一个新的BigDecimal对象,因为BigInteger与BigDecimal都是不可变的(immutable)的,在进行每一步运算时,都会产生一个新的对象
代码演示:
package com.Test;
import Test2.MyDate;
import java.math.BigDecimal;
public class Main {
private final static String name = "磊哥的java历险记-@51博客";
public static void main(String[] args){
BigDecimal a = new BigDecimal("4.5");
BigDecimal b = new BigDecimal("1.5");
a. add(b);
System.out.println(a); //输出4.5. 加减乘除方法会返回一个新的
System.out.println("============="+name+"=============");
}
}
5、总结
(1)商业计算使用BigDecimal。
(2)尽量使用参数类型为String的构造函数。
(3)BigDecimal都是不可变的(immutable)的,在进行每一步运算时,都会产wf 所以在做加减乘除运算时千万要保存操作后的值。
(4)我们往往容易忽略JDK底层的一些实现细节,导致出现错误,需要多加注意。
6、精炼练习
在银行结算或支付中,我们经常会用到BigDecimal的相关方法。
6.1 题目
(1)使用BigDecimal创建出浮点类型的数字
(2)使用BigDecimal进行加减乘除运算
6.2 实验步骤
(1)声明一个类Test
(2)在Test类中,完成BigDecimal的构造和方法使用
代码演示:
package com.Test;
import Test2.MyDate;
import java.math.BigDecimal;
public class Main {
private final static String name = "磊哥的java历险记-@51博客";
public static void main(String[] args){
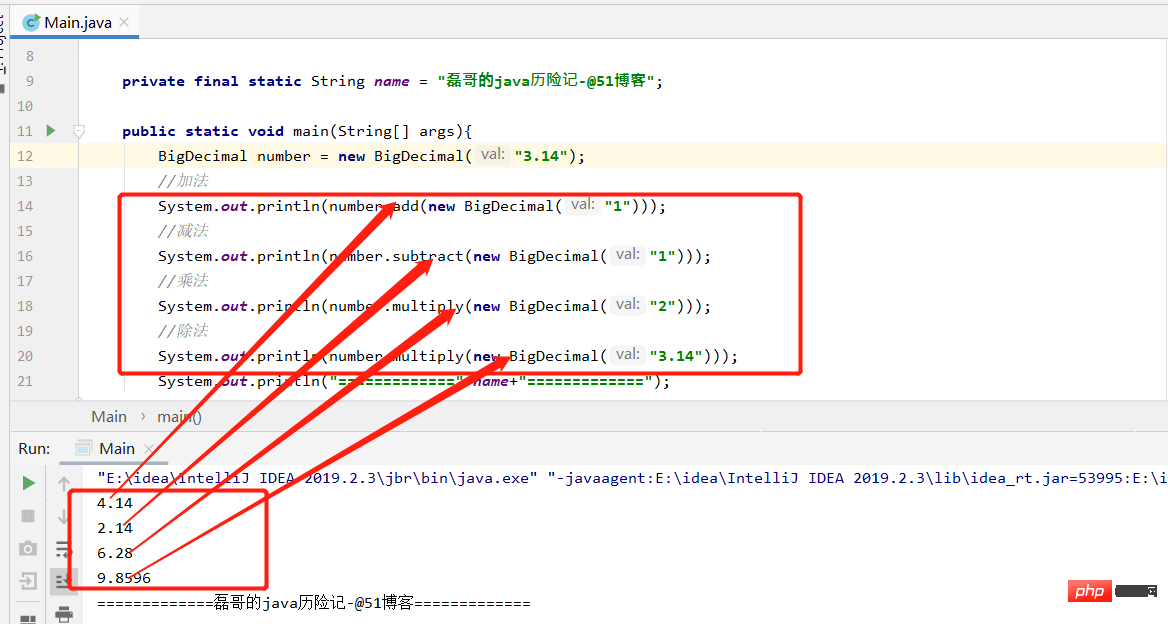
BigDecimal number = new BigDecimal("3.14");
//加法
System.out.println(number.add(new BigDecimal("1")));
//减法
System.out.println(number.subtract(new BigDecimal("1")));
//乘法
System.out.println(number.multiply(new BigDecimal("2")));
//除法
System.out.println(number.multiply(new BigDecimal("3.14")));
System.out.println("============="+name+"=============");
}
}
Das obige ist der detaillierte Inhalt vonBeispielcodeanalyse für eine Java-BigDecimal-Klassenanwendung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 Perfekte Zahl in Java
Aug 30, 2024 pm 04:28 PM
Perfekte Zahl in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur perfekten Zahl in Java. Hier besprechen wir die Definition, Wie prüft man die perfekte Zahl in Java?, Beispiele mit Code-Implementierung.
 Zufallszahlengenerator in Java
Aug 30, 2024 pm 04:27 PM
Zufallszahlengenerator in Java
Aug 30, 2024 pm 04:27 PM
Leitfaden zum Zufallszahlengenerator in Java. Hier besprechen wir Funktionen in Java anhand von Beispielen und zwei verschiedene Generatoren anhand ihrer Beispiele.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden für Weka in Java. Hier besprechen wir die Einführung, die Verwendung von Weka Java, die Art der Plattform und die Vorteile anhand von Beispielen.
 Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Smith-Nummer in Java
Aug 30, 2024 pm 04:28 PM
Leitfaden zur Smith-Zahl in Java. Hier besprechen wir die Definition: Wie überprüft man die Smith-Nummer in Java? Beispiel mit Code-Implementierung.
 Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
Fragen zum Java Spring-Interview
Aug 30, 2024 pm 04:29 PM
In diesem Artikel haben wir die am häufigsten gestellten Fragen zu Java Spring-Interviews mit ihren detaillierten Antworten zusammengestellt. Damit Sie das Interview knacken können.
 Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Java 8 führt die Stream -API ein und bietet eine leistungsstarke und ausdrucksstarke Möglichkeit, Datensammlungen zu verarbeiten. Eine häufige Frage bei der Verwendung von Stream lautet jedoch: Wie kann man von einem Foreach -Betrieb brechen oder zurückkehren? Herkömmliche Schleifen ermöglichen eine frühzeitige Unterbrechung oder Rückkehr, aber die Stream's foreach -Methode unterstützt diese Methode nicht direkt. In diesem Artikel werden die Gründe erläutert und alternative Methoden zur Implementierung vorzeitiger Beendigung in Strahlverarbeitungssystemen erforscht. Weitere Lektüre: Java Stream API -Verbesserungen Stream foreach verstehen Die Foreach -Methode ist ein Terminalbetrieb, der einen Vorgang für jedes Element im Stream ausführt. Seine Designabsicht ist
 Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Zeitstempel für Datum in Java
Aug 30, 2024 pm 04:28 PM
Anleitung zum TimeStamp to Date in Java. Hier diskutieren wir auch die Einführung und wie man Zeitstempel in Java in ein Datum konvertiert, zusammen mit Beispielen.
 Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Java -Programm, um das Kapselvolumen zu finden
Feb 07, 2025 am 11:37 AM
Kapseln sind dreidimensionale geometrische Figuren, die aus einem Zylinder und einer Hemisphäre an beiden Enden bestehen. Das Volumen der Kapsel kann berechnet werden, indem das Volumen des Zylinders und das Volumen der Hemisphäre an beiden Enden hinzugefügt werden. In diesem Tutorial wird erörtert, wie das Volumen einer bestimmten Kapsel in Java mit verschiedenen Methoden berechnet wird. Kapselvolumenformel Die Formel für das Kapselvolumen lautet wie folgt: Kapselvolumen = zylindrisches Volumenvolumen Zwei Hemisphäre Volumen In, R: Der Radius der Hemisphäre. H: Die Höhe des Zylinders (ohne die Hemisphäre). Beispiel 1 eingeben Radius = 5 Einheiten Höhe = 10 Einheiten Ausgabe Volumen = 1570,8 Kubikeinheiten erklären Berechnen Sie das Volumen mithilfe der Formel: Volumen = π × R2 × H (4




