

Rekursion ist in der Tat eine relativ abstrakte mathematische Logik, die einfach als „das Programm ruft seinen eigenen Algorithmus auf“ verstanden werden kann.
Wikipedias Erklärung der Rekursion lautet:
Rekursion (englisch: Rekursion), in der Mathematik und Informatik auch als Rekursion übersetzt, bezieht sich auf die Methode, die Funktion selbst in der Definition der Funktion zu verwenden. Der Begriff Rekursion wird auch häufiger verwendet, um den Prozess der selbstähnlichen Wiederholung von Dingen zu beschreiben.
Wenn beispielsweise zwei Spiegel ungefähr parallel zueinander sind, erscheinen die in den Spiegeln verschachtelten Bilder in Form einer unendlichen Rekursion. Es kann auch als Prozess der Selbstreplikation verstanden werden.
„Pass“ bedeutet weitergeben und „Return“ bedeutet, zuerst eine Methode Schicht für Schicht zu übergeben, sie dann an die letzte Schicht zu übergeben und das Ergebnis zurückzugeben.
Ich stand zum Beispiel in der Schlange für einen Nukleinsäuretest und vor mir standen 100 Leute. Ich wollte fragen, wann das medizinische Personal Feierabend machen würde, also fragte ich den Bruder vor mir , und er fragte die Leute vor ihm und reichte es einer nach dem anderen weiter. Schließlich wurde es an das medizinische Personal weitergegeben, das antwortete, dass sie um 18 Uhr Feierabend machen würden. Dieser Satz wurde zurückgeschickt und erreichte mich schließlich. Ich wusste, dass das medizinische Personal um sechs Uhr Feierabend hatte.
Dieser Prozess ist ein rekursiver Prozess. Wenn die „Übergabe einer Nachricht“ selbst eine Methode ist, ruft der gesamte Prozess der Übermittlung einer Nachricht seine eigene Methode auf und erhält schließlich das Ergebnis.
Das ist etwas anderes als der Zyklus. Der Zyklus ist gleichbedeutend mit dem Aufsetzen von Kopfhörern auf alle, und dann wird ein „Vermittler“ Sie nacheinander fragen, ob Sie wissen, wann das medizinische Personal von der Arbeit kommt. Sie werden die Antwort bekommen. Die „Agentur“ sagte mir, dass ich um sechs Uhr Feierabend machen würde.
Im Wesentlichen besteht die Rekursion darin, ein großes Problem, wie das Schälen einer Zwiebel, kontinuierlich zu zerlegen und es schließlich auf die kleinste Ebene zu zerlegen und das Lösungsergebnis zurückzugeben.
Verwenden Sie Python, um das einfachste Beispiel einer rekursiven Funktion zu geben und darüber zu sprechen, was rekursive Anwendungen sind.
Wir sehen häufig Funktionen, die sich selbst aufrufen, um Schleifenoperationen zu implementieren, beispielsweise Funktionen zum Finden von Fakultäten.
Die Fakultät der ganzen Zahl n ist n*(n-1)*(n-2)*...*3*2*1.
Zum Beispiel können die folgenden 5 Zeilen Python-Code die Berechnung der Fakultät realisieren.
def fact(n): ''' n表示要求的数的阶乘 ''' if n==1: return n n = n*fact(n-1) return n print(factorial(5))
Viele Leute sind möglicherweise verwirrt über die Berechnungslogik hier, warum die Faktenfunktion sich selbst aufruft und schließlich das Ergebnis erhält.
Wir können es gemäß der mathematischen Logik ableiten:
Die Fakultät der ganzen Zahl n ist: fact(n) = n*(n-1)*...*3*2*1.
Die Fakultät der ganzen Zahl n-1 ist: fact(n-1) = (n-1)*(n-2)*...*3*2*1.
Daher kann gefolgert werden, dass fact(n) = n*fact(n-1).
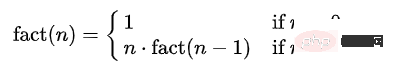
Gibt es eine Faktenmethode, die für jede Zahl aufgerufen werden kann? Wenn n=1 schließlich aufgerufen wird, wird die Fakultät des Ergebnisses n zurückgegeben.
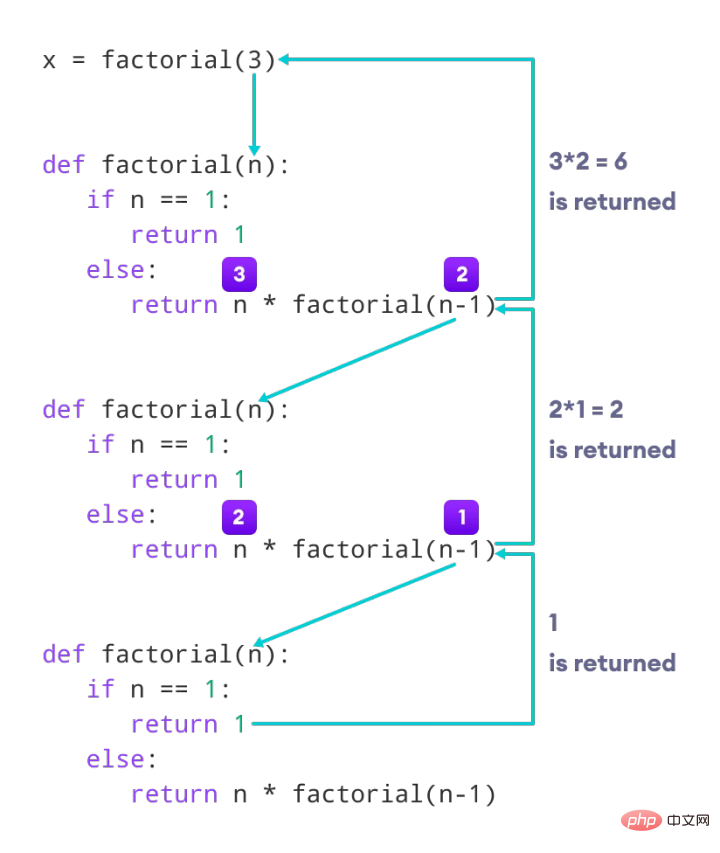
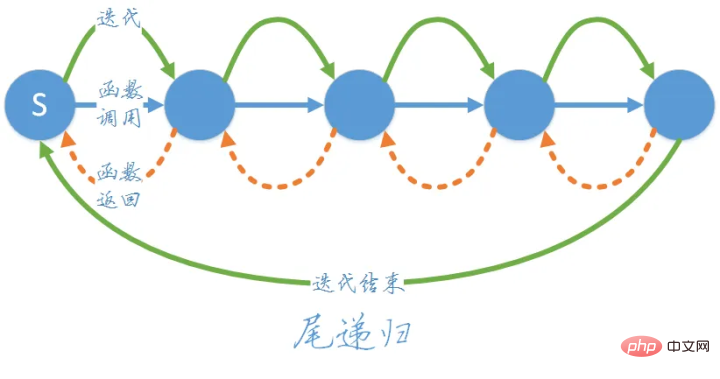
Sehen Sie sich das Bild oben an. Die rekursive Funktion wird Schicht für Schicht nach unten aufgerufen. Wenn schließlich n = 1 ist, wird das Ergebnis nach oben zurückgegeben.
Dies ist der gesamte Prozess der Rekursion. Wenn wir die Rekursion genau definieren, können wir sie in den folgenden drei Punkten zusammenfassen:
1 Es gibt mindestens eine klare Endbedingung für die Rekursion.
2. Geben Sie die Lösung an, wenn die Rekursion beendet ist.
3. Jedes Mal, wenn Sie eine tiefere Rekursionsebene betreten, sollte die Problemgröße (Berechnungsmenge) im Vergleich zur letzten Rekursion reduziert werden.
Nehmen Sie den obigen Code als Beispiel:
def factorial(n): ''' n表示要求的数的阶乘 ''' if n==1: # 1、明确递归终止条件; return n # 2、递归终止时的处理办法 n = n*factorial(n-1) # 递去 return n# 归来
Neben häufigen faktoriellen Fällen gibt es auch Fibonacci-Folgen, die ebenfalls klassische Anwendungen der Rekursion sind.
Fibonacci-Folge: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...
Diese Sequenz beginnt mit dem 3. Element, jedes Element entspricht der Summe der beiden vorherigen Elemente.
Es ist rekursiv wie folgt definiert: F(0)=0, F(1)=1, F(n)=F(n - 1)+F(n - 2)(n≥ 2, n∈N* ).
In Python können wir rekursive Funktionen verwenden, um die Fibonacci-Folge zu implementieren:
# 1,1,2,3,5,8,13,21,34,55,试判断数列第12个数是哪个? def fab(n): ''' n为斐波那契数列 ''' if n <= 2: v = 1 return v v = fab(n-1)+fab(n-2) return v print(fab(12))
Verwenden Sie mathematische Methoden, um Folgendes abzuleiten:
Tatsächlich können die beiden oben genannten rekursiven Fälle durch mathematische Induktion erklärt werden, bei der es sich um das Wissen der High-School-Mathematik handelt.
Um einen Satz P(n) in Bezug auf eine natürliche Zahl n zu beweisen, gibt es im Allgemeinen die folgenden Schritte:
(1) Beweisen Sie, dass der Satz wahr ist, wenn n den ersten Wert n0 annimmt. n0 nimmt für allgemeine Folgen den Wert 0 oder 1 an, es gibt aber auch Sonderfälle.
(2) Nehmen Sie an, dass der Satz wahr ist, wenn n=k (k≥n0, k ist eine natürliche Zahl), und beweisen Sie, dass der Satz auch wahr ist, wenn n=k+1.
Bei der Synthese von (1) (2) ist für alle natürlichen Zahlen n (≥n0) der Satz P(n) wahr.
Zusätzlich zu den mathematischen Erklärungen habe ich zuvor auch jemanden gesehen, der eine anschaulichere Erklärung der Rekursion gegeben hat:
1、我们已经完成了吗?如果完成了,返回结果。如果没有这样的终止条件,递归将会永远地继续下去。
2、如果没有,则简化问题,解决较容易的问题,并将结果组装成原始问题的解决办法。然后返回该解决办法。
哈哈,到这里大家是不是对递归有了一个更加深刻的认识。
如果还不清楚,没关系,这里还有更多的递归案例,用Python来实现,可以说非常简洁。
def gcd(m, n): if n == 0: return m else: return gcd(n, m%n)
def sumnums(n): if n == 1: return 1 return n + sumnums(n - 1) print(sumnums(3))
def reverse(string): if len(string) == 0: return string else: return reverse(string[1:]) + string[0] reverseme = '我是帅哥' print(reverse(reverseme))
def towerOfHanoi(numrings, from_pole, to_pole, aux_pole):
if numrings == 1:
print('Move ring 1 from', from_pole, 'pole to', to_pole, 'pole')
return
towerOfHanoi(numrings - 1, from_pole, aux_pole, to_pole)
print('Move ring', numrings, 'from', from_pole, 'pole to', to_pole, 'pole')
towerOfHanoi(numrings - 1, aux_pole, to_pole, from_pole)
numrings = 2
towerOfHanoi(numrings, 'Left', 'Right', 'Middle')
data = [1,3,6,13,56,123,345,1024,3223,6688]
def dichotomy(min,max,d,n):
'''
min表示有序列表头部索引
max表示有序列表尾部索引
d表示有序列表
n表示需要寻找的元素
'''
mid = (min+max)//2
if mid==0:
return 'None'
elif d[mid]<n:
print('向右侧找!')
return dichotomy(mid,max,d,n)
elif d[mid]>n:
print('向左侧找!')
return dichotomy(min,mid,d,n)
else:
print('找到了%s'%d[mid])
return
res = dichotomy(0,len(data),data,222)
print(res)
有位大佬说过:To Iterate is Human, to Recurse, Divine。
中文译为:人理解迭代,神理解递归。
可见递归是非常神奇的算法,它的神奇之处在于它允许用户用有限的语句描述无限的对象。
当然人无完人,递归也是有缺点的,它一般效率较低,且会导致调用栈溢出。
因为递归不断调用自身函数,且产生大量变量,而栈空间的容量是有限的,循环太多就会效率低下,甚至导致调用栈溢出。
Das obige ist der detaillierte Inhalt vonWie kann man rekursive Algorithmen besser verstehen? Detaillierte Erklärung von Python-Beispielen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




