Was sind die Grundkenntnisse und Konzepte von Binärbäumen in Java?

1. Baumstruktur

1.1 Konzept

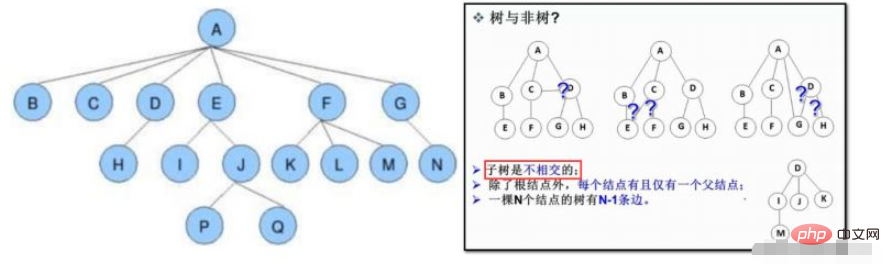
Baum ist eine nichtlineare Datenstruktur, bei der es sich um eine Reihe hierarchischer Beziehungen handelt, die aus n (n>=0) begrenzten Knoten bestehen. Man nennt ihn Baum, weil er aussieht wie ein umgedrehter Baum, das heißt, die Wurzeln zeigen nach oben und die Blätter nach unten.

1.2 Konzept (Wichtig)

a Der Grad des Knotens: die Anzahl der Teilbäume des Knotens; wie oben gezeigt: Der Grad von A ist 6, der Grad von J ist 2

b Grad des Baumes: Die Zahl des Baumes, der Grad des größten Knotens ist der Grad der Zahl; wie in der Abbildung oben gezeigt: Der Grad des Baumes ist 6

c Knoten mit Grad 0 (Knoten ohne Teilbaum)

d. Übergeordneter Knoten Punkt/übergeordneter Knoten: Wie im Bild oben gezeigt: D ist der übergeordnete Knoten von H

Untergeordneter Knoten/untergeordneter Knoten: Wie im Bild oben gezeigt : H ist der untergeordnete Knoten von D

e. Wurzelknoten: Ein Knoten ohne Eltern, wie im Bild oben gezeigt: A

f. Die Ebene des Knotens: Ausgehend von der Definition der Wurzel ist die Wurzel erste Ebene, die untergeordneten Knoten der Wurzel sind die zweite Ebene und so weiter;

g Die Höhe oder Tiefe des Baums: die maximale Ebene des Knotens im Baum; 4

2. Binärbaum (Schlüsselpunkt)

2.1 Konzept

Jeder Knoten hat höchstens zwei Teilbäume, Grad

2.2 Die Grundform des Binärbaums

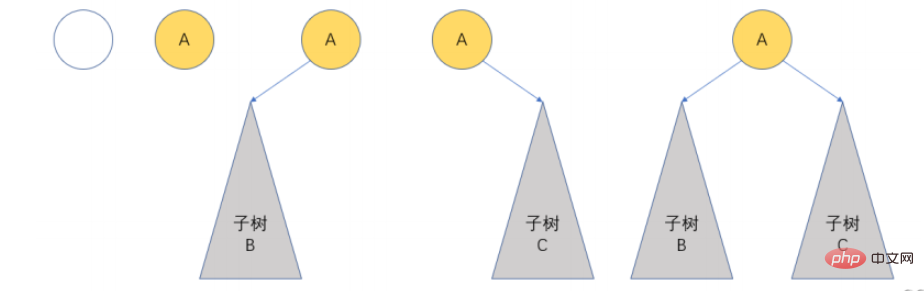
2.3 Zwei Arten Spezieller Binärbaum

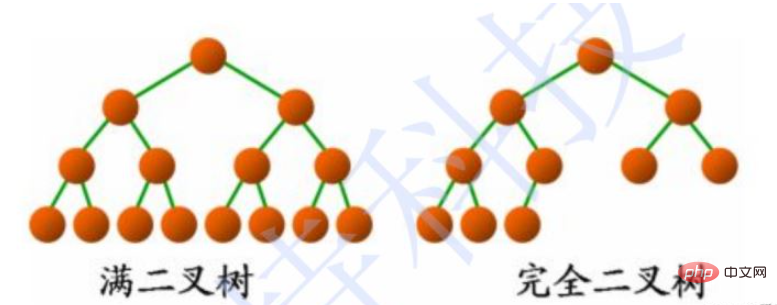
a. Vollständiger Binärbaum: Nicht-Keimblatt-Grad ist 2

b Vollständiger Binärbaum: Die „untere rechte Ecke“ fehlt

2.4 Eigenschaften von Binärbäumen

a Baum

1. Die Höhe ist K, dann gibt es 2^k-1 Knoten

2 Die Ebene ist K, dann hat die Ebene 2^(k-1) Knoten

3 Anzahl der Knoten - 1

4. Es gibt n0 mit Grad 0 und n2 mit Grad 2, dann ist n0 = n2 + 1

b. Wenn es ein richtiges Kind gibt, muss es eines geben ein linkes Kind

2. Es kann nur einen Knoten mit Grad 1 geben

2.5 Speicherung des Binärbaums

Die Speicherstruktur des Binärbaums ist unterteilt in: sequentielle Speicherung und verknüpfte Speicherung ähnlich einer verknüpften Liste.

Sequentieller Speicher: Es können nur vollständige Binärbäume gespeichert werden.

Kettenspeicher: Gewöhnliche Binärbäume.

Dieses Mal zeigen wir den Kettenspeicher.

Der Kettenspeicher von Binärbäumen wird von Knoten einzeln referenziert. Die übliche Darstellung ist binär und Ternäre Darstellung,

Nehmen Sie dieses Bild als Beispiel, die Details sind wie folgt: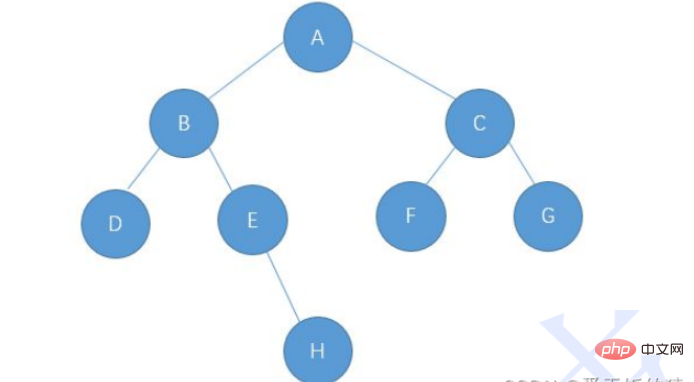

// 孩子表示法
private static class TreeNode{
    char val;
    TreeNode left;
    TreeNode right;
 
    public TreeNode(char val) {
        this.val = val;
    }
}

Initialisierung:

    public static TreeNode build(){
        TreeNode nodeA=new TreeNode('A');
        TreeNode nodeB=new TreeNode('B');
        TreeNode nodeC=new TreeNode('C');
        TreeNode nodeD=new TreeNode('D');
        TreeNode nodeE=new TreeNode('E');
        TreeNode nodeF=new TreeNode('F');
        TreeNode nodeG=new TreeNode('G');
        TreeNode nodeH=new TreeNode('H');
        nodeA.left=nodeB;
        nodeA.right=nodeC;
        nodeB.left=nodeD;
        nodeB.right=nodeE;
        nodeE.right=nodeH;
        nodeC.left=nodeF;
        nodeC.right=nodeG;
        return nodeA;
    }

2.6 Grundoperationen von Binärbäumen

2.6.1 Binärbaumdurchquerung (Rekursion)

1. NLR: ehemalige Vorbestellungsdurchquerung (auch bekannt als Vorbestellungsdurchquerung) – Besuchen Sie den Wurzelknoten ---> den rechten Teilbaum der Wurzel.

    //先序遍历 : 根左右
    public static void preOrder(TreeNode root){
        if(root==null){
            return;
        }
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

2. Inorder Traversal (Inorder Traversal) – Der linke Teilbaum der Wurzel --->

    //中序遍历
    public static void inOrder(TreeNode root){
        if(root==null){
            return;
        }
        preOrder(root.left);
        System.out.print(root.val+" ");
        preOrder(root.right);
    }

3. LRN: Postorder Traversal – linker Teilbaum des Wurzelknotens --->

    //后序遍历
    public static void postOrder(TreeNode root){
        if(root==null){
            return;
        }
        preOrder(root.left);
        preOrder(root.right);
        System.out.print(root.val+" ");
    }

2.6.2 Binärbaumdurchquerung (Iteration)

1. Vorbestellungsdurchquerung

    //方法2(迭代)
    //先序遍历 (迭代)
    public static void preOrderNonRecursion(TreeNode root){
        if(root==null){
            return ;
        }
        Deque<TreeNode> stack=new LinkedList<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode cur=stack.pop();
            System.out.print(cur.val+" ");
            if(cur.right!=null){
                stack.push(cur.right);
            }
            if(cur.left!=null){
                stack.push(cur.left);
            }
        }
    }

3. Nachbestellungsdurchquerung

    //方法2(迭代)
    //中序遍历 (迭代)
    public static void inorderTraversalNonRecursion(TreeNode root) {
        if(root==null){
            return ;
        }
 
        Deque<TreeNode> stack=new LinkedList<>();
        // 当前走到的节点
        TreeNode cur=root;
        while (!stack.isEmpty() || cur!=null){
            // 不管三七二十一，先一路向左走到根儿~
            while (cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
            // 此时cur为空，说明走到了null，此时栈顶就存放了左树为空的节点
            cur=stack.pop();
            System.out.print(cur.val+" ");
            // 继续访问右子树
            cur=cur.right;
        }
    }

1. Finden Sie die Anzahl Knoten (Rekursion und Iteration)

    //方法2(迭代)
    //后序遍历 (迭代)
    public static void postOrderNonRecursion(TreeNode root){
        if(root==null){
            return;
        }
        Deque<TreeNode> stack=new LinkedList<>();
        TreeNode cur=root;
        TreeNode prev=null;
 
        while (!stack.isEmpty() || cur!=null){
            while (cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
 
            cur=stack.pop();
            if(cur.right==null || prev==cur.right){
                System.out.print(cur.val+" ");
                prev=cur;
                cur=null;
            }else {
                stack.push(cur);
                cur=cur.right;
            }
        }
    }

2. Ermitteln Sie die Anzahl der Blattknoten (Rekursion und Iteration)

    //方法1(递归)
    //传入一颗二叉树的根节点，就能统计出当前二叉树中一共有多少个节点，返回节点数
    //此时的访问就不再是输出节点值，而是计数器 + 1操作
    public static int getNodes(TreeNode root){
        if(root==null){
            return 0;
        }
        return 1+getNodes(root.left)+getNodes(root.right);
    }
 
    //方法2(迭代)
    //使用层序遍历来统计当前树中的节点个数
    public static int getNodesNoRecursion(TreeNode root){
        if(root==null){
            return 0;
        }
        int size=0;
        Deque<TreeNode> queue=new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            size++;
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
        return size;
    }

. Ermitteln Sie die Anzahl der Knoten in der k-ten Ebene

    //方法1(递归)
    //传入一颗二叉树的根节点，就能统计出当前二叉树的叶子结点个数
    public static int getLeafNodes(TreeNode root){
        if(root==null){
            return 0;
        }
        if(root.left==null && root.right==null){
            return 1;
        }
        return getLeafNodes(root.left)+getLeafNodes(root.right);
    }
 
    //方法2(迭代)
    //使用层序遍历来统计叶子结点的个数
    public static int getLeafNodesNoRecursion(TreeNode root){
        if(root==null){
            return 0;
        }
        int size=0;
        Deque<TreeNode> queue=new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            TreeNode cur=queue.poll();
            if(cur.left==null && cur.right==null){
                size++;
            }
            if(cur.left!=null){
                queue.offer(cur.left);
            }
            if(cur.right!=null){
                queue.offer(cur.right);
            }
        }
        return size;
    }

5. Bestimmen Sie, ob es einen Knoten mit einem Wert in der Binärbaumnummer gibt

Das obige ist der detaillierte Inhalt vonWas sind die Grundkenntnisse und Konzepte von Binärbäumen in Java?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!